Numerical Measures Numerical Measures Measures of Central Tendency







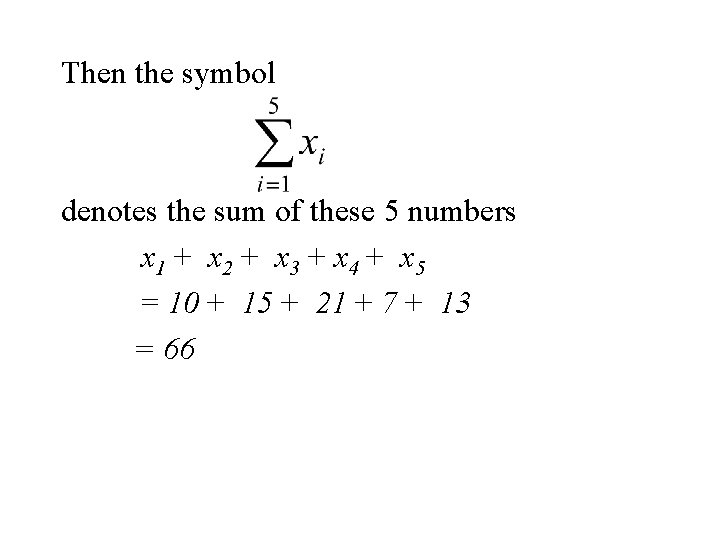


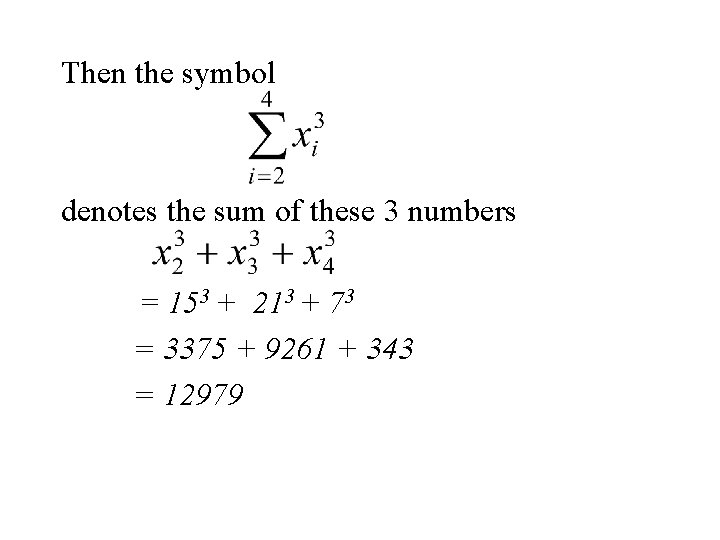

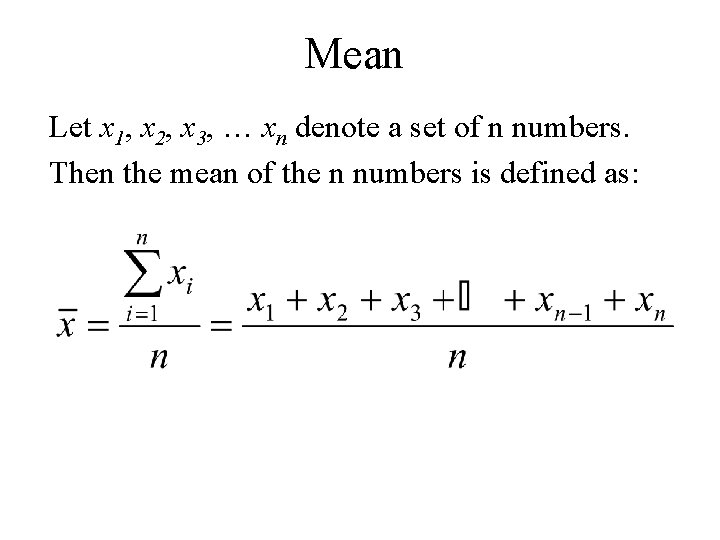

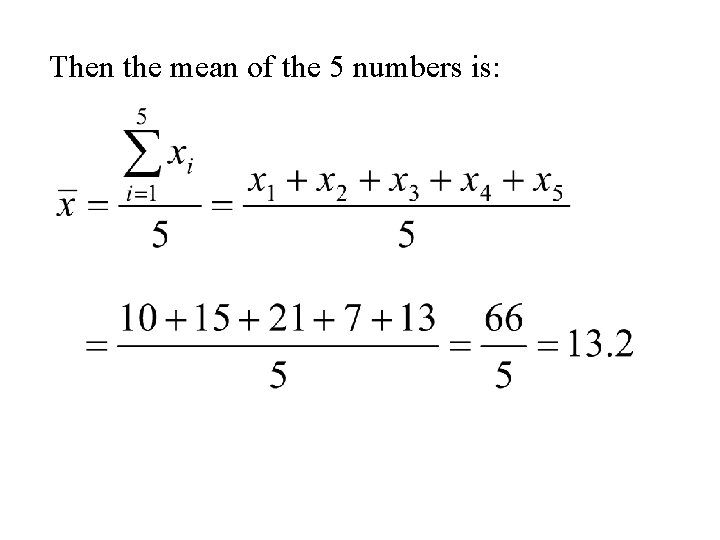















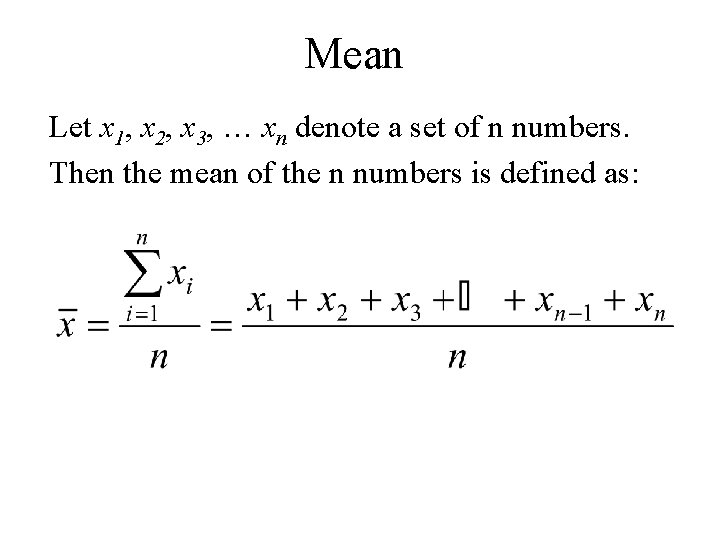















































- Slides: 113

Numerical Measures

Numerical Measures • • Measures of Central Tendency (Location) Measures of Non Central Location Measure of Variability (Dispersion, Spread) Measures of Shape

Measures of Central Tendency (Location) • Mean • Median • Mode Central Location

Measures of Non-central Location • Quartiles, Mid-Hinges • Percentiles Non - Central Location

Measure of Variability (Dispersion, Spread) • Variance, standard deviation • Range • Inter-Quartile Range Variability

Measures of Shape • Skewness • Kurtosis

Summation Notation

Summation Notation Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the symbol denotes the sum of these n numbers x 1 + x 2 + x 3 + …+ xn

Example Let x 1, x 2, x 3, x 4, x 5 denote a set of 5 denote the set of numbers in the following table. i 1 2 3 4 5 xi 10 15 21 7 13
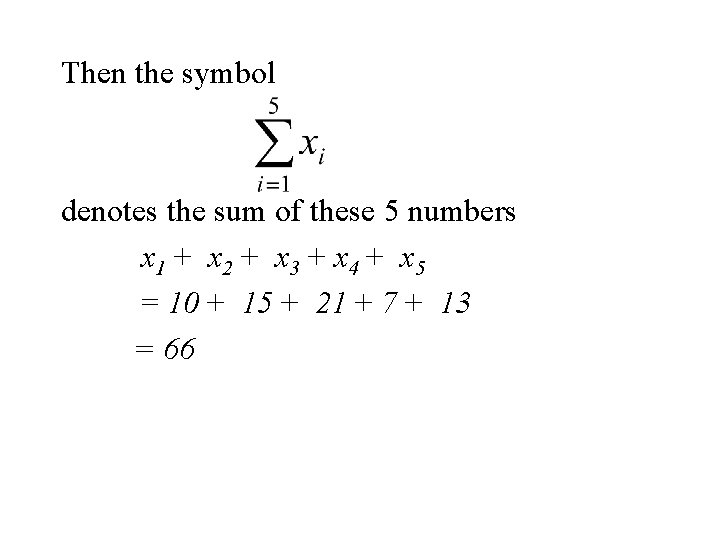
Then the symbol denotes the sum of these 5 numbers x 1 + x 2 + x 3 + x 4 + x 5 = 10 + 15 + 21 + 7 + 13 = 66

Meaning of parts of summation notation Final value for i each term of the sum Quantity changing in each term of the sum Starting value for i

Example Again let x 1, x 2, x 3, x 4, x 5 denote a set of 5 denote the set of numbers in the following table. i 1 2 3 4 5 xi 10 15 21 7 13
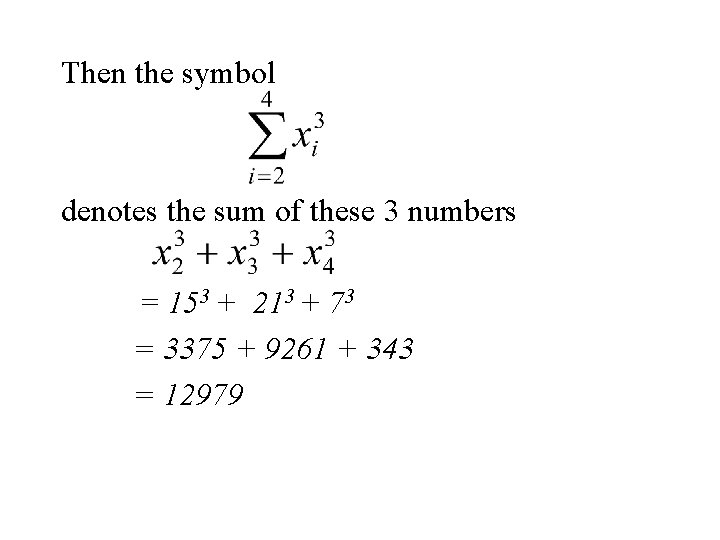
Then the symbol denotes the sum of these 3 numbers = 153 + 213 + 73 = 3375 + 9261 + 343 = 12979

Measures of Central Location (Mean)
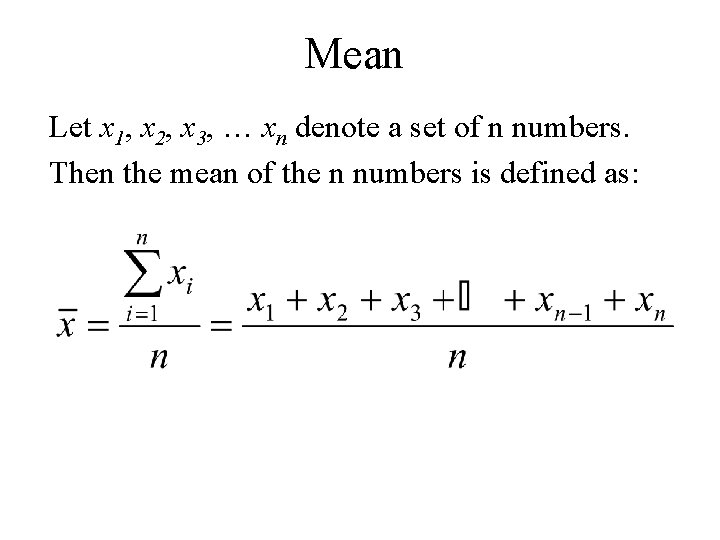
Mean Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the mean of the n numbers is defined as:

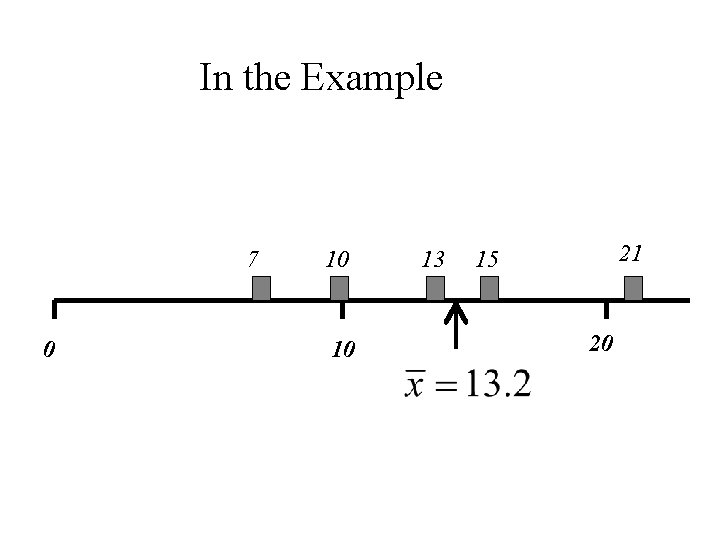
Example Again let x 1, x 2, x 3, x 4, x 5 denote a set of 5 denote the set of numbers in the following table. i 1 2 3 4 5 xi 10 15 21 7 13
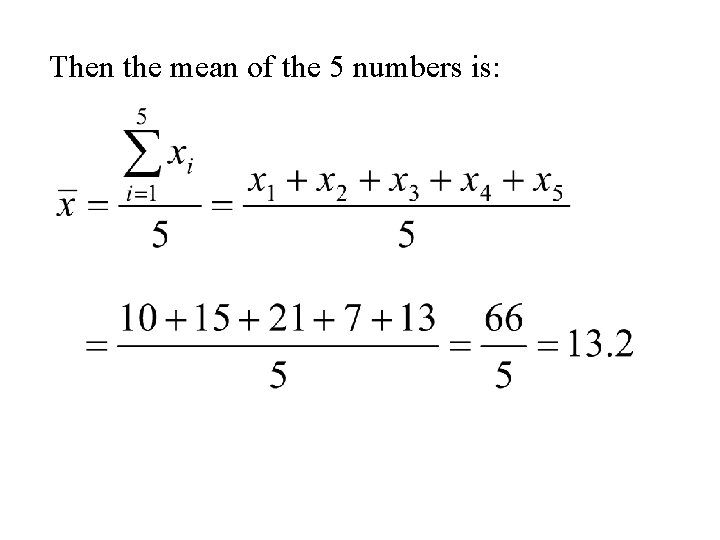
Then the mean of the 5 numbers is:

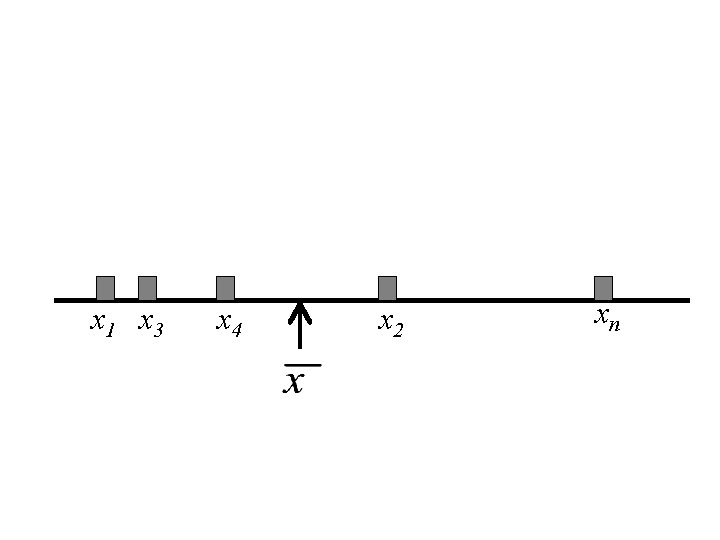
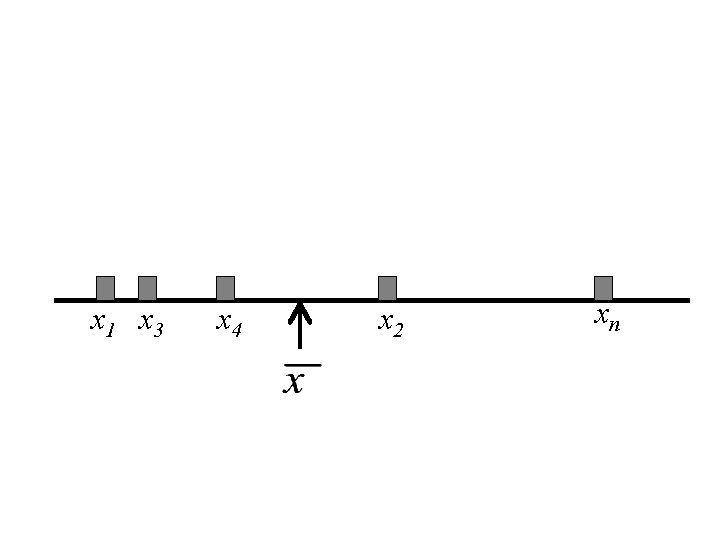
Interpretation of the Mean Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the mean, , is the centre of gravity of those the n numbers. That is if we drew a horizontal line and placed a weight of one at each value of xi , then the balancing point of that system of mass is at the point .

x 1 x 3 x 4 x 2 xn

In the Example 7 0 10 10 13 21 15 20

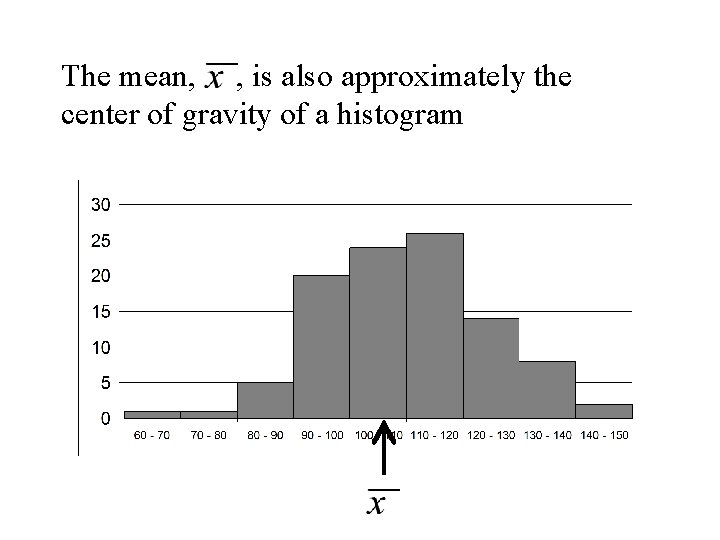
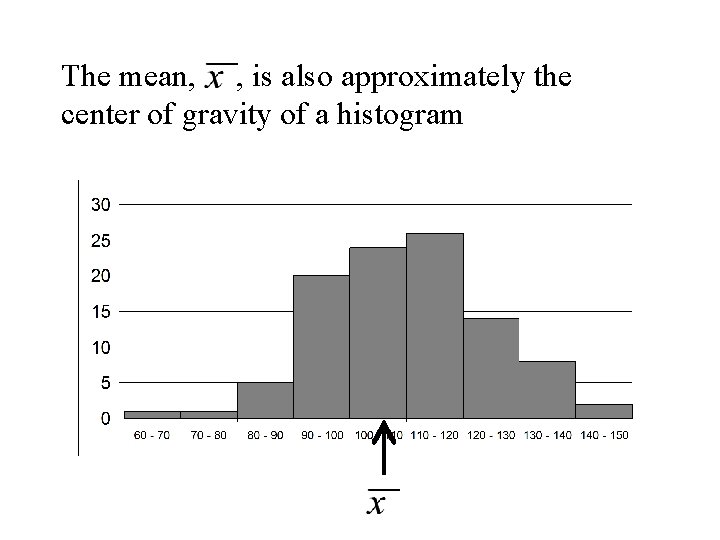
The mean, , is also approximately the center of gravity of a histogram

Measures of Central Location (Median)

The Median Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the median of the n numbers is defined as the number that splits the numbers into two equal parts. To evaluate the median we arrange the numbers in increasing order.

If the number of observations is odd there will be one observation in the middle. This number is the median. If the number of observations is even there will be two middle observations. The median is the average of these two observations

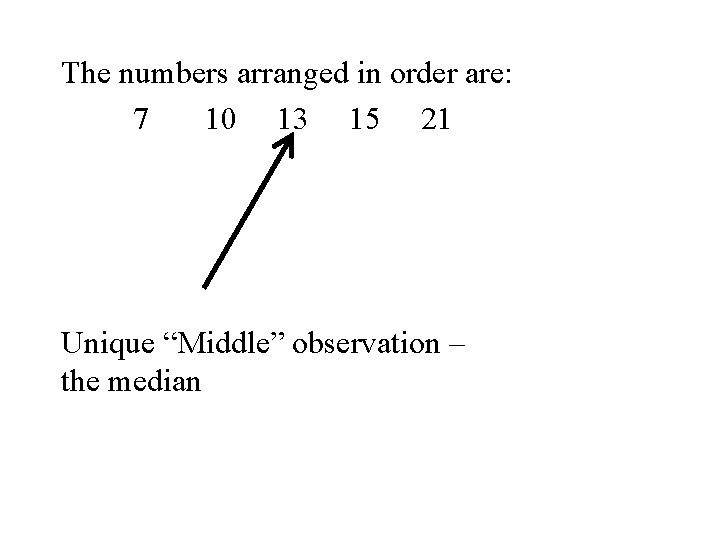
Example Again let x 1, x 2, x 3 , x 4, x 5 denote a set of 5 denote the set of numbers in the following table. i 1 2 3 4 5 xi 10 15 21 7 13

The numbers arranged in order are: 7 10 13 15 21 Unique “Middle” observation – the median

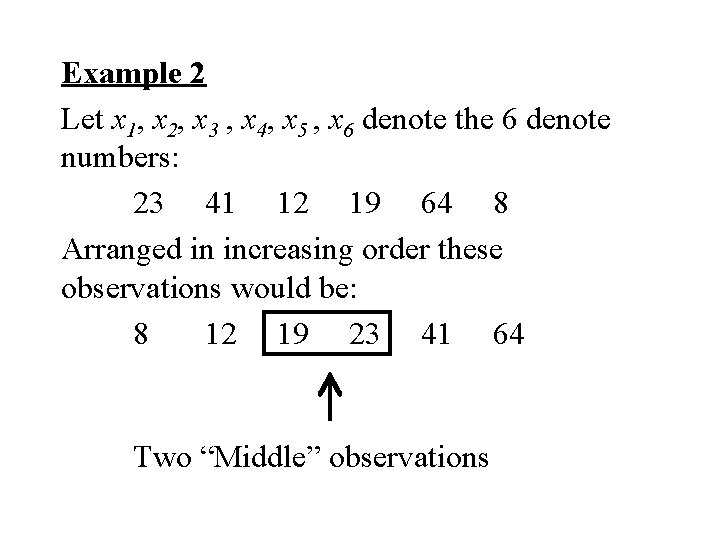
Example 2 Let x 1, x 2, x 3 , x 4, x 5 , x 6 denote the 6 denote numbers: 23 41 12 19 64 8 Arranged in increasing order these observations would be: 8 12 19 23 41 64 Two “Middle” observations

Median = average of two “middle” observations =

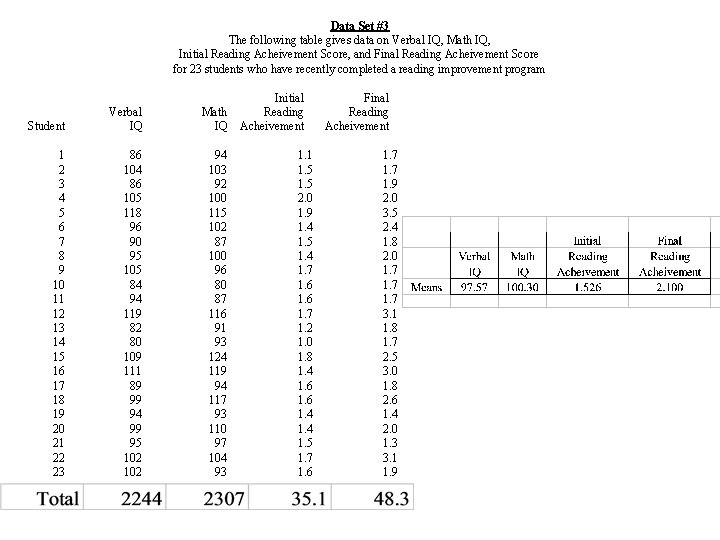
Example The data on N = 23 students Variables • Verbal IQ • Math IQ • Initial Reading Achievement Score • Final Reading Achievement Score

Student Verbal IQ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 86 104 86 105 118 96 90 95 105 84 94 119 82 80 109 111 89 99 94 99 95 102 Data Set #3 The following table gives data on Verbal IQ, Math IQ, Initial Reading Acheivement Score, and Final Reading Acheivement Score for 23 students who have recently completed a reading improvement program Initial Final Math Reading IQ Acheivement 94 103 92 100 115 102 87 100 96 80 87 116 91 93 124 119 94 117 93 110 97 104 93 1. 1 1. 5 2. 0 1. 9 1. 4 1. 5 1. 4 1. 7 1. 6 1. 7 1. 2 1. 0 1. 8 1. 4 1. 6 1. 4 1. 5 1. 7 1. 6 1. 7 1. 9 2. 0 3. 5 2. 4 1. 8 2. 0 1. 7 3. 1 1. 8 1. 7 2. 5 3. 0 1. 8 2. 6 1. 4 2. 0 1. 3 3. 1 1. 9

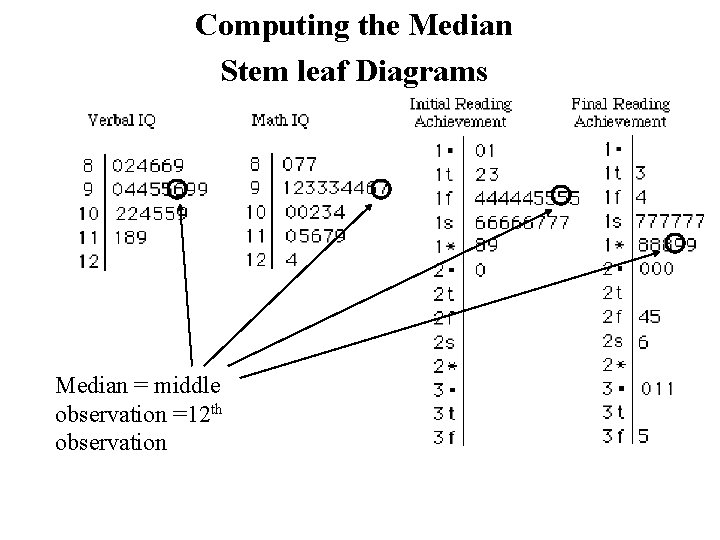
Computing the Median Stem leaf Diagrams Median = middle observation =12 th observation

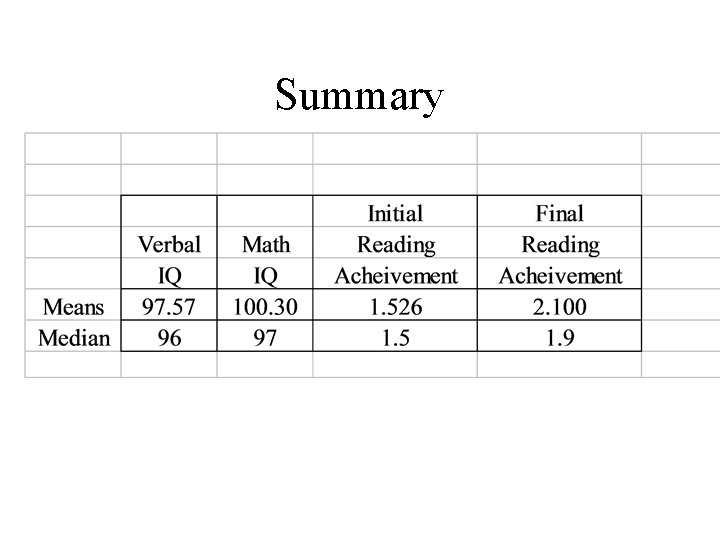
Summary

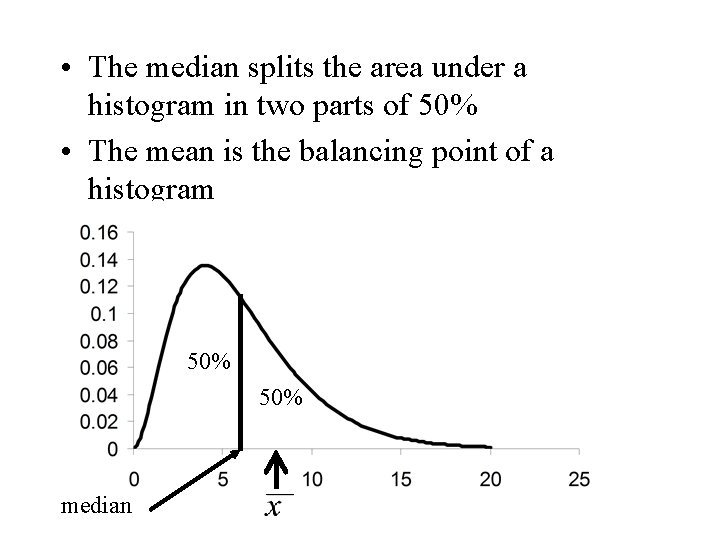
Some Comments • The mean is the centre of gravity of a set of observations. The balancing point. • The median splits the obsevations equally in two parts of approximately 50%

• The median splits the area under a histogram in two parts of 50% • The mean is the balancing point of a histogram 50% median

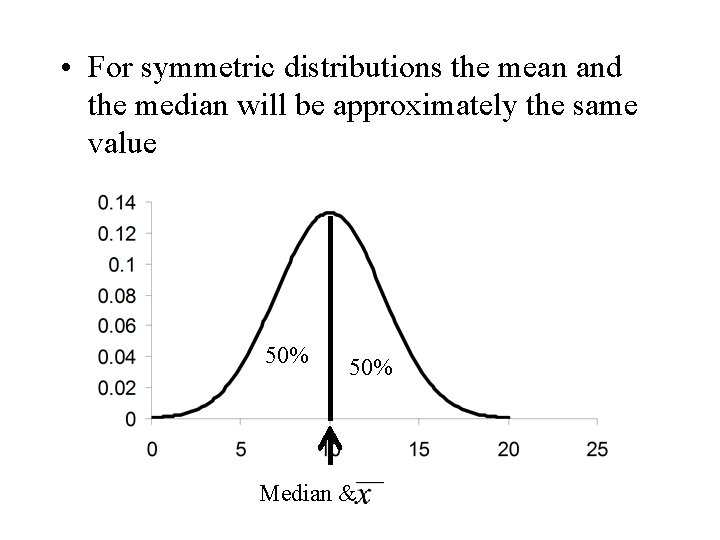
• For symmetric distributions the mean and the median will be approximately the same value 50% Median &

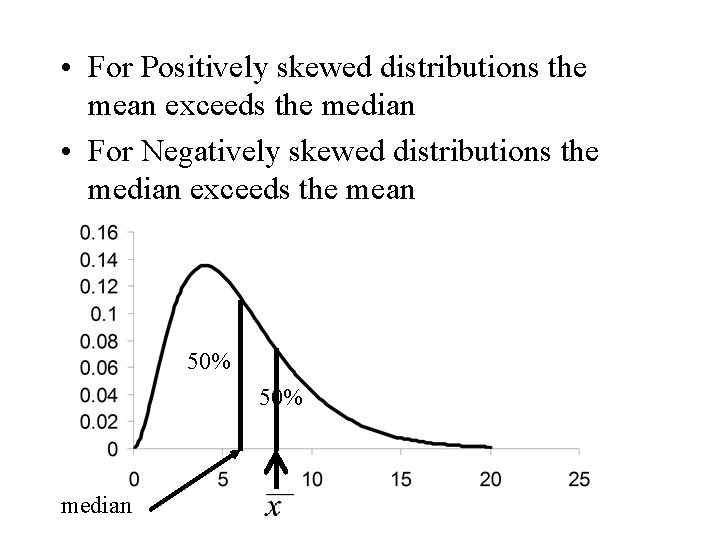
• For Positively skewed distributions the mean exceeds the median • For Negatively skewed distributions the median exceeds the mean 50% median

• An outlier is a “wild” observation in the data • Outliers occur because – of errors (typographical and computational) – Extreme cases in the population

• The mean is altered to a significant degree by the presence of outliers • Outliers have little effect on the value of the median • This is a reason for using the median in place of the mean as a measure of central location • Alternatively the mean is the best measure of central location when the data is Normally distributed (Bell-shaped)

Review

Summarizing Data Graphical Methods

Histogram Stem-Leaf Diagram Grouped Freq Table

Numerical Measures • • Measures of Central Tendency (Location) Measures of Non Central Location Measure of Variability (Dispersion, Spread) Measures of Shape The objective is to reduce the data to a small number of values that completely describe the data and certain aspects of the data.

Measures of Central Location (Mean)
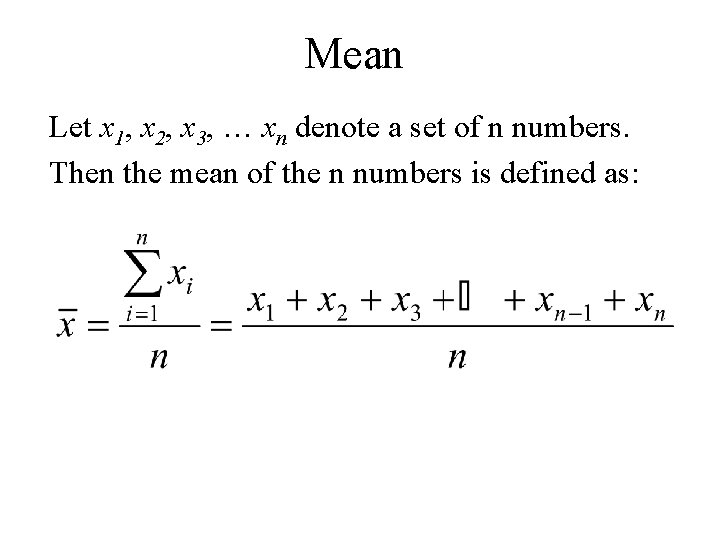
Mean Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the mean of the n numbers is defined as:

Interpretation of the Mean Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the mean, , is the centre of gravity of those the n numbers. That is if we drew a horizontal line and placed a weight of one at each value of xi , then the balancing point of that system of mass is at the point .

x 1 x 3 x 4 x 2 xn

The mean, , is also approximately the center of gravity of a histogram

The Median Let x 1, x 2, x 3, … xn denote a set of n numbers. Then the median of the n numbers is defined as the number that splits the numbers into two equal parts. To evaluate the median we arrange the numbers in increasing order.

If the number of observations is odd there will be one observation in the middle. This number is the median. If the number of observations is even there will be two middle observations. The median is the average of these two observations

Measures of Non-Central Location • • Percentiles Quartiles (Hinges, Mid-hinges)

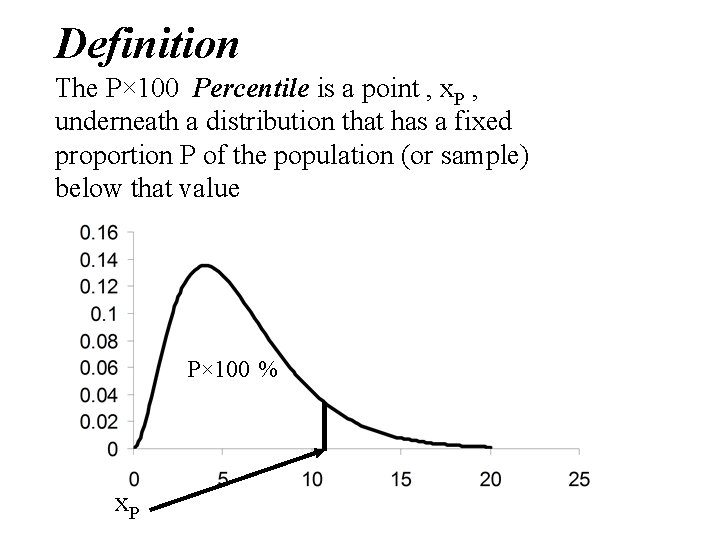
Definition The P× 100 Percentile is a point , x. P , underneath a distribution that has a fixed proportion P of the population (or sample) below that value P× 100 % x. P

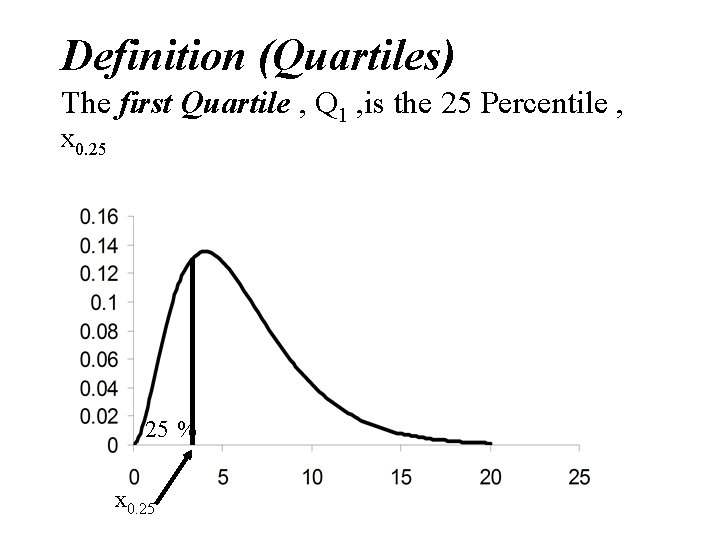
Definition (Quartiles) The first Quartile , Q 1 , is the 25 Percentile , x 0. 25 25 % x 0. 25

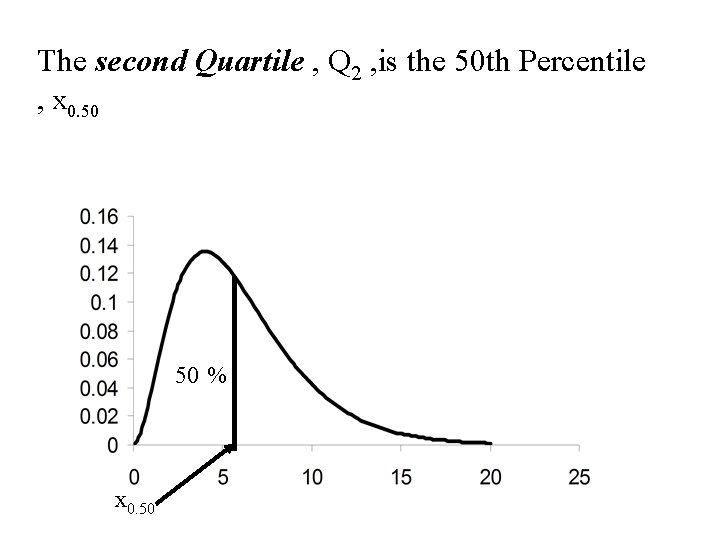
The second Quartile , Q 2 , is the 50 th Percentile , x 0. 50 50 % x 0. 50

• The second Quartile , Q 2 , is also the median and the 50 th percentile

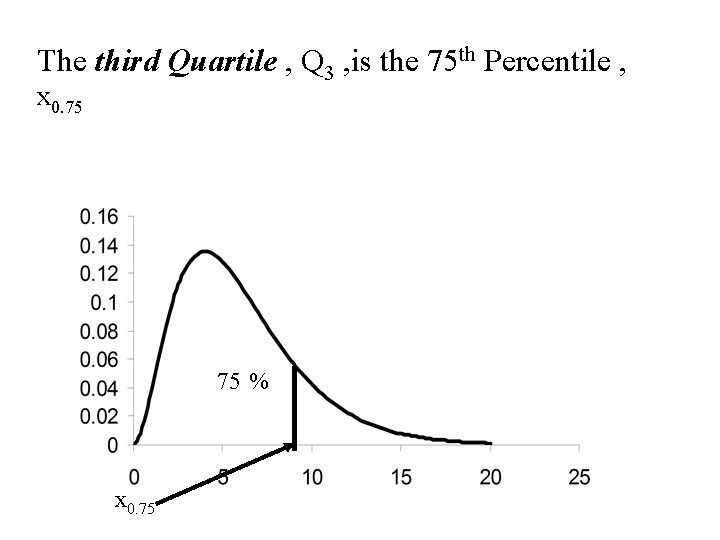
The third Quartile , Q 3 , is the 75 th Percentile , x 0. 75 75 % x 0. 75

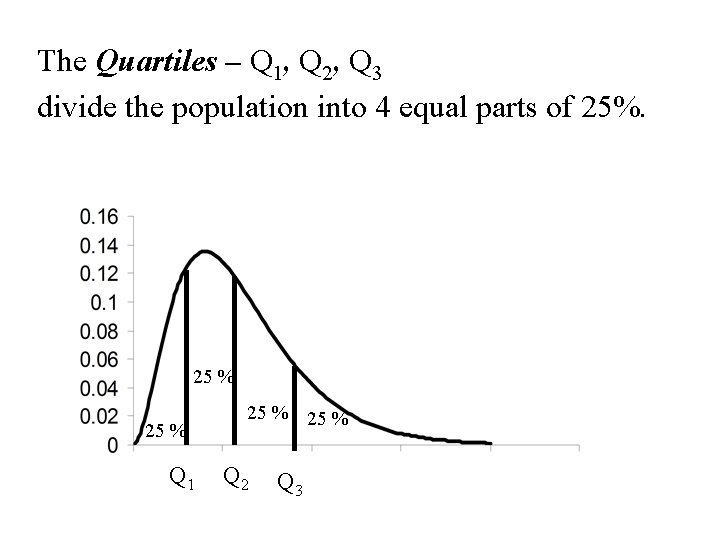
The Quartiles – Q 1, Q 2, Q 3 divide the population into 4 equal parts of 25%. 25 % Q 1 25 % Q 2 Q 3

Computing Percentiles and Quartiles • There are several methods used to compute percentiles and quartiles. Different computer packages will use different methods • Sometimes for small samples these methods will agree (but not always) • For large samples the methods will agree within a certain level of accuracy

Computing Percentiles and Quartiles – Method 1 • The first step is to order the observations in increasing order. • We then compute the position, k, of the P× 100 Percentile. k = P × (n+1) Where n = the number of observations

Example The data on n = 23 students Variables • Verbal IQ • Math IQ • Initial Reading Achievement Score • Final Reading Achievement Score We want to compute the 75 th percentile and the 90 th percentile

The position, k, of the 75 th Percentile. k = P × (n+1) =. 75 × (23+1) = 18 The position, k, of the 90 th Percentile. k = P × (n+1) =. 90 × (23+1) = 21. 6 When the position k is an integer the percentile is the kth observation (in order of magnitude) in the data set. For example the 75 th percentile is the 18 th (in size) observation

When the position k is an not an integer but an integer(m) + a fraction(f). i. e. k = m + f then the percentile is x. P = (1 -f) × (mth observation in size) + f × (m+1 st observation in size) In the example the position of the 90 th percentile is: k = 21. 6 Then x. 90 = 0. 4(21 st observation in size) + 0. 6(22 nd observation in size)

When the position k is an not an integer but an integer(m) + a fraction(f). i. e. k = m + f then the percentile is x. P = (1 -f) × (mth observation in size) + f × (m+1 st observation in size) mth obs (m+1)st obs xp = (1 - f) ( mth obs) + f [(m+1)st obs]

When the position k is an not an integer but an integer(m) + a fraction(f). i. e. k = m + f mth obs (m+1)st obs xp = (1 - f) ( mth obs) + f [(m+1)st obs] Thus the position of xp is 100 f% through the interval between the mth observation and the (m +1)st observation

Example The data Verbal IQ on n = 23 students arranged in increasing order is: 80 82 84 86 86 89 90 94 94 95 95 96 99 99 102 104 105 109 111 118 119

x 0. 75 = 75 th percentile = 18 th observation in size =105 (position k = 18) x 0. 90 = 90 th percentile = 0. 4(21 st observation in size) + 0. 6(22 nd observation in size) = 0. 4(111)+ 0. 6(118) = 115. 2 (position k = 21. 6)

An Alternative method for computing Quartiles – Method 2 • Sometimes this method will result in the same values for the quartiles. • Sometimes this method will result in the different values for the quartiles. • For large samples the two methods will result in approximately the same answer.

Let x 1, x 2, x 3, … xn denote a set of n numbers. The first step in Method 2 is to arrange the numbers in increasing order. From the arranged numbers we compute the median. This is also called the Hinge

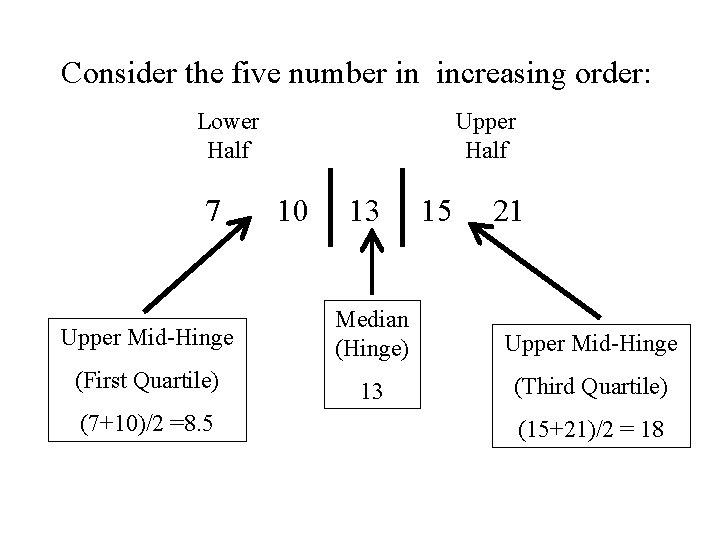
Example Consider the 5 numbers: 10 15 21 7 13 Arranged in increasing order: 7 10 13 15 21 Median (Hinge) The median (or Hinge) splits the observations in half

The lower mid-hinge (the first quartile) is the “median” of the lower half of the observations (excluding the median). The upper mid-hinge (the third quartile) is the “median” of the upper half of the observations (excluding the median).

Consider the five number in increasing order: Lower Upper Half 7 Half 10 13 15 21 Upper Mid-Hinge Median (Hinge) Upper Mid-Hinge (First Quartile) 13 (Third Quartile) (7+10)/2 =8. 5 (15+21)/2 = 18

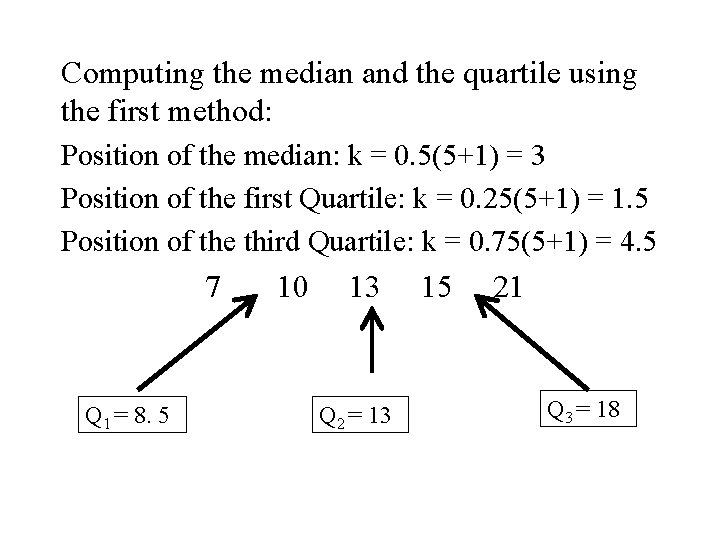
Computing the median and the quartile using the first method: Position of the median: k = 0. 5(5+1) = 3 Position of the first Quartile: k = 0. 25(5+1) = 1. 5 Position of the third Quartile: k = 0. 75(5+1) = 4. 5 7 Q 1 = 8. 5 10 13 Q 2 = 13 15 21 Q 3 = 18

• Both methods result in the same value • This is not always true.

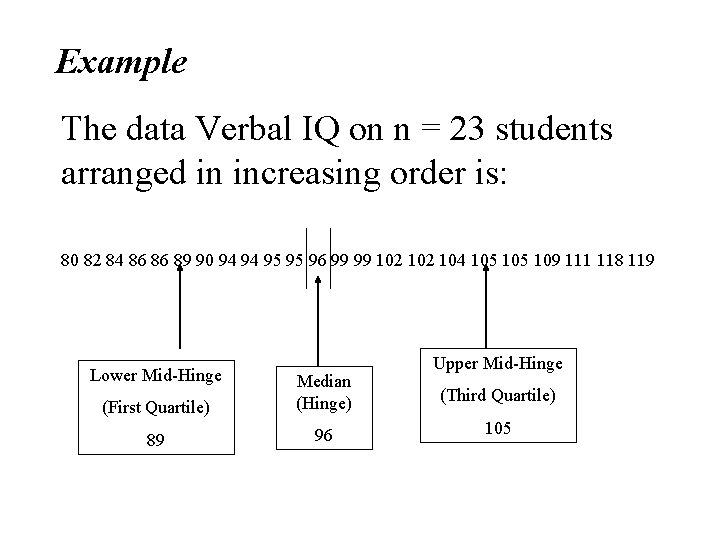
Example The data Verbal IQ on n = 23 students arranged in increasing order is: 80 82 84 86 86 89 90 94 94 95 95 96 99 99 102 104 105 109 111 118 119 Lower Mid-Hinge (First Quartile) Median (Hinge) 89 96 Upper Mid-Hinge (Third Quartile) 105

Computing the median and the quartile using the first method: Position of the median: k = 0. 5(23+1) = 12 Position of the first Quartile: k = 0. 25(23+1) = 6 Position of the third Quartile: k = 0. 75(23+1) = 18 80 82 84 86 86 89 90 94 94 95 95 96 99 99 102 104 105 109 111 118 119 Q 1 = 89 Q 2 = 96 Q 3 = 105

• Many programs compute percentiles, quartiles etc. • Each may use different methods. • It is important to know which method is being used. • The different methods result in answers that are close when the sample size is large.

Announcement Assignment 2 has been posted this assignment has to be handed in and is due Friday, January 22 This assignment requires the use of a Statistical Package (SPSS or Minitab) available in most computer labs. Instructions on the use of these packages will be given in the lab today

Box-Plots Box-Whisker Plots • A graphical method of displaying data • An alternative to the histogram and stem-leaf diagram

To Draw a Box Plot • Compute the Hinge (Median, Q 2) and the Mid-hinges (first & third quartiles – Q 1 and Q 3 ) • We also compute the largest and smallest of the observations – the max and the min • The five number summary min, Q 1, Q 2, Q 3, max

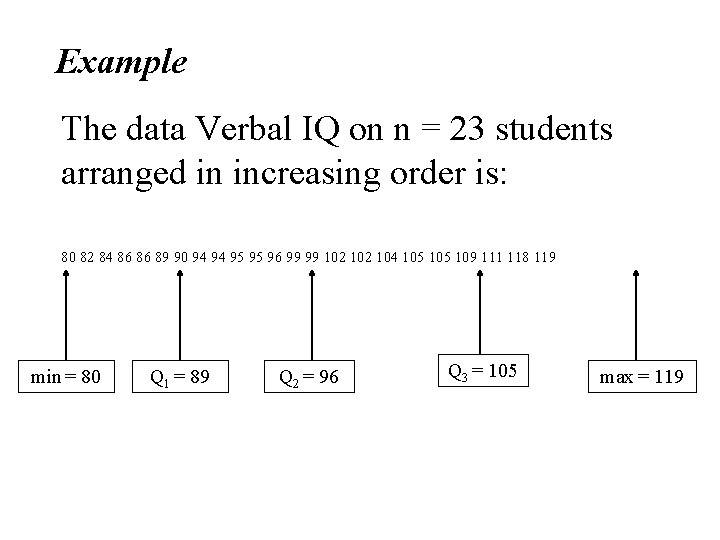
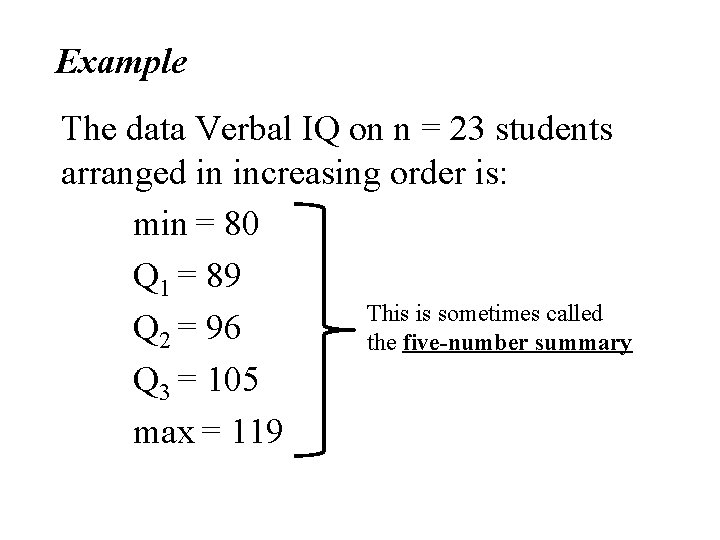
Example The data Verbal IQ on n = 23 students arranged in increasing order is: 80 82 84 86 86 89 90 94 94 95 95 96 99 99 102 104 105 109 111 118 119 min = 80 Q 1 = 89 Q 2 = 96 Q 3 = 105 max = 119

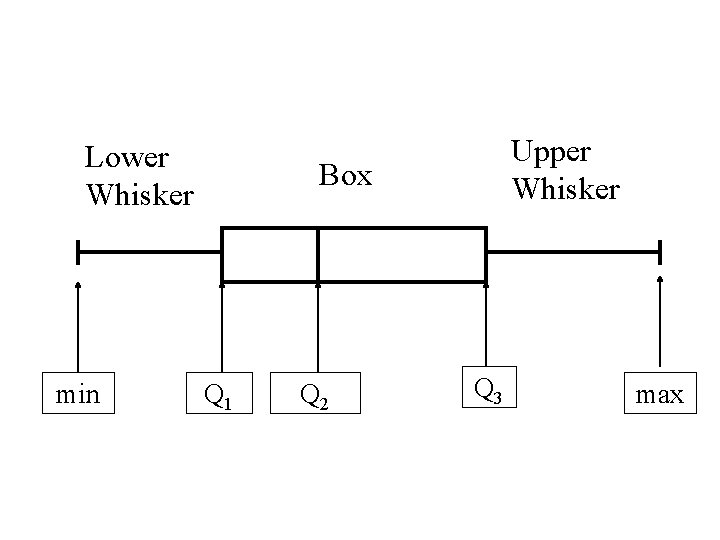
The Box Plot is then drawn • Drawing above an axis a “box” from Q 1 to Q 3. • Drawing vertical line in the box at the median, Q 2 • Drawing whiskers at the lower and upper ends of the box going down to the min and up to max.

Lower Whisker min Upper Whisker Box Q 1 Q 2 Q 3 max

Example The data Verbal IQ on n = 23 students arranged in increasing order is: min = 80 Q 1 = 89 This is sometimes called Q 2 = 96 the five-number summary Q 3 = 105 max = 119

Box Plot of Verbal IQ 70 80 90 100 110 120 130

130 120 110 100 90 80 70 Box Plot can also be drawn vertically

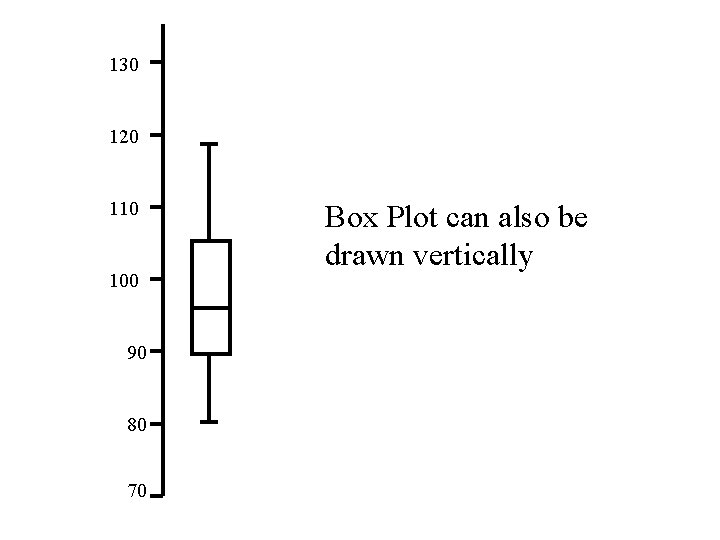
Box-Whisker plots (Verbal IQ, Math IQ)

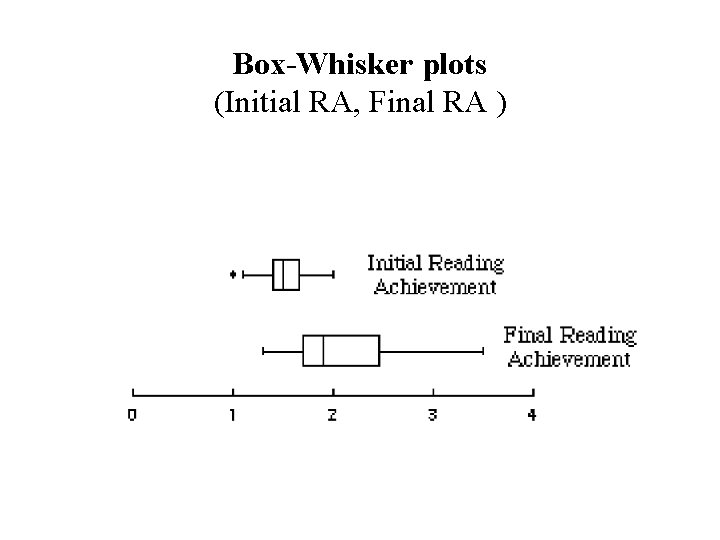
Box-Whisker plots (Initial RA, Final RA )

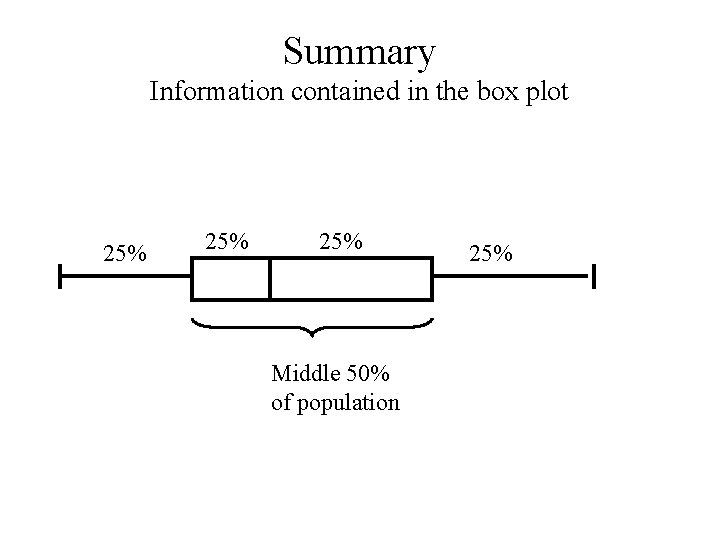
Summary Information contained in the box plot 25% 25% Middle 50% of population 25%

Advance Box Plots

• An outlier is a “wild” observation in the data • Outliers occur because – of errors (typographical and computational) – Extreme cases in the population • We will now consider the drawing of boxplots where outliers are identified

To Draw a Box Plot we need to: • Compute the Hinge (Median, Q 2) and the Mid-hinges (first & third quartiles – Q 1 and Q 3 ) • The difference Q 3– Q 1 is called the interquartile range (denoted by IQR) • To identify outliers we will compute the inner and outer fences

The fences are like the fences at a prison. We expect the entire population to be within both sets of fences. If a member of the population is between the inner and outer fences it is a mild outlier. If a member of the population is outside of the outer fences it is an extreme outlier.

Inner fences

Lower inner fence f 1 = Q 1 - (1. 5)IQR Upper inner fence f 2 = Q 3 + (1. 5)IQR

Outer fences

Lower outer fence F 1 = Q 1 - (3)IQR Upper outer fence F 2 = Q 3 + (3)IQR

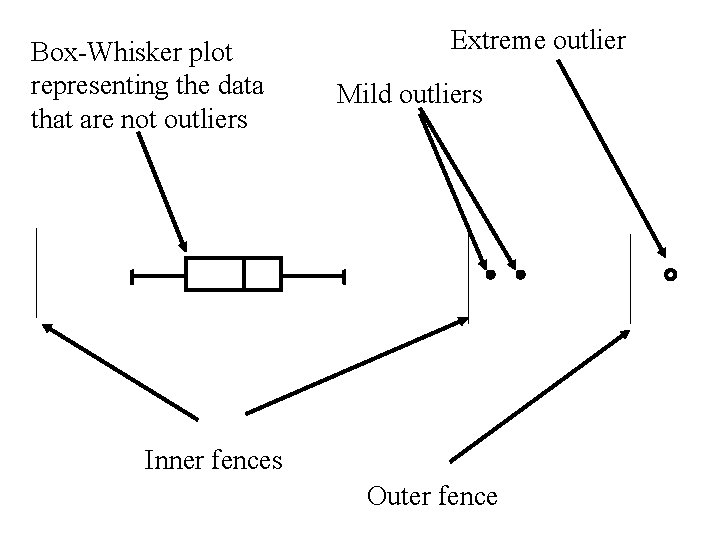
• Observations that are between the lower and upper inner fences are considered to be nonoutliers. • Observations that are outside the inner fences but not outside the outer fences are considered to be mild outliers. • Observations that are outside outer fences are considered to be extreme outliers.

• mild outliers are plotted individually in a box-plot using the symbol • extreme outliers are plotted individually in a box-plot using the symbol • non-outliers are represented with the box and whiskers with – Max = largest observation within the fences – Min = smallest observation within the fences

Box-Whisker plot representing the data that are not outliers Extreme outlier Mild outliers Inner fences Outer fence

Example Data collected on n = 109 countries in 1995. Data collected on k = 25 variables.

The variables 1. Population Size (in 1000 s) 2. Density = Number of people/Sq kilometer 3. Urban = percentage of population living in cities 4. Religion 5. lifeexpf = Average female life expectancy 6. lifeexpm = Average male life expectancy

7. literacy = % of population who read 8. pop_inc = % increase in popn size (1995) 9. babymort = Infant motality (deaths per 1000) 10. gdp_cap = Gross domestic product/capita 11. Region = Region or economic group 12. calories = Daily calorie intake. 13. aids = Number of aids cases 14. birth_rt = Birth rate per 1000 people

15. death_rt = death rate per 1000 people 16. aids_rt = Number of aids cases/100000 people 17. log_gdp = log 10(gdp_cap) 18. log_aidsr = log 10(aids_rt) 19. b_to_d =birth to death ratio 20. fertility = average number of children in family 21. log_pop = log 10(population)

22. cropgrow = ? ? 23. lit_male = % of males who can read 24. lit_fema = % of females who can read 25. Climate = predominant climate

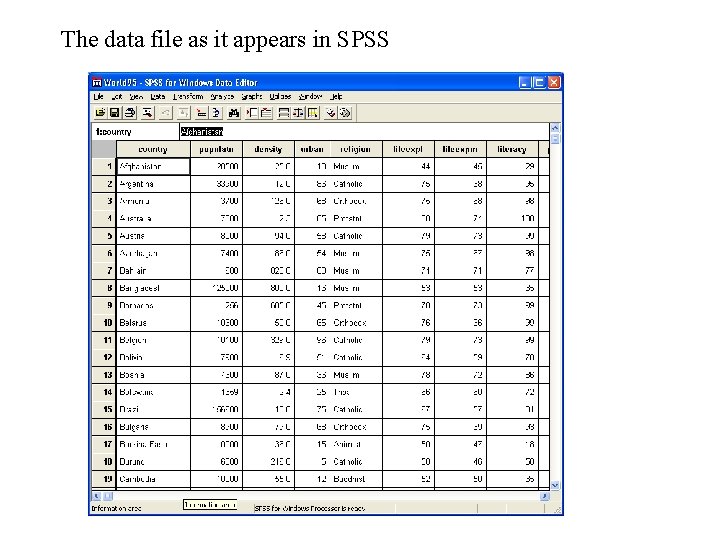
The data file as it appears in SPSS

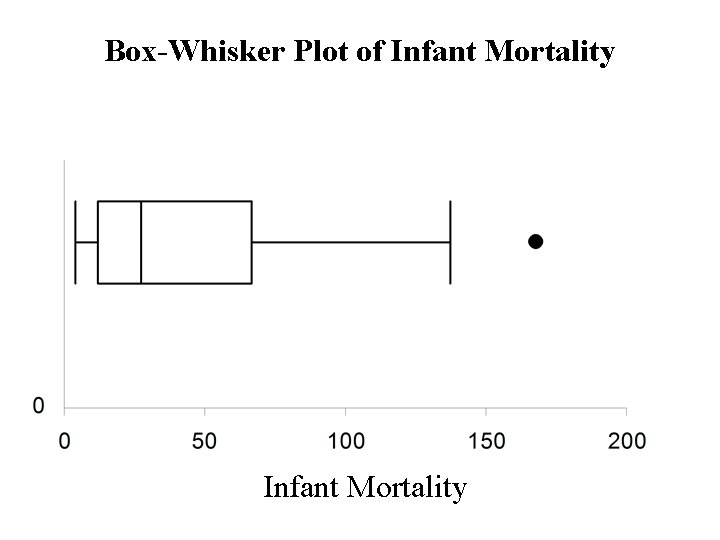
Consider the data on infant mortality Stem-Leaf diagram stem = 10 s, leaf = unit digit

Summary Statistics median = Q 2 = 27 Quartiles Lower quartile = Q 1 = the median of lower half Upper quartile = Q 3 = the median of upper half Interquartile range (IQR) IQR = Q 1 - Q 3 = 66. 5 – 12 = 54. 5

The Outer Fences lower = Q 1 - 3(IQR) = 12 – 3(54. 5) = - 151. 5 upper = Q 3 = 3(IQR) = 66. 5 + 3(54. 5) = 230. 0 No observations are outside of the outer fences The Inner Fences lower = Q 1 – 1. 5(IQR) = 12 – 1. 5(54. 5) = - 69. 75 upper = Q 3 = 1. 5(IQR) = 66. 5 + 1. 5(54. 5) = 148. 25 Only one observation (168 – Afghanistan) is outside of the inner fences – (mild outlier)

Box-Whisker Plot of Infant Mortality

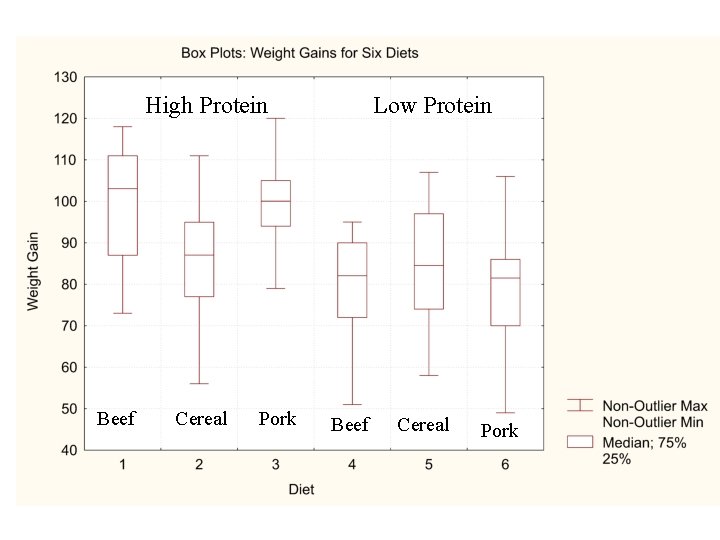
Example 2 In this example we are looking at the weight gains (grams) for rats under six diets differing in level of protein (High or Low) and source of protein (Beef, Cereal, or Pork). – Ten test animals for each diet

Table Gains in weight (grams) for rats under six diets differing in level of protein (High or Low) and source of protein (Beef, Cereal, or Pork) High Protein Level Source Diet Median Mean IQR PSD Variance Std. Dev. Low protein Beef Cereal Pork Beef Cereal Pork 1 73 102 118 104 81 107 100 87 111 103. 0 100. 0 24. 0 17. 78 229. 11 15. 14 2 98 74 56 111 95 88 82 77 86 92 87. 0 85. 9 18. 0 13. 33 225. 66 15. 02 3 94 79 96 98 102 108 91 120 105 100. 0 99. 5 11. 0 8. 15 119. 17 10. 92 4 90 76 90 64 86 51 72 90 95 78 82. 0 79. 2 18. 0 13. 33 192. 84 13. 89 5 107 95 97 80 98 74 74 67 89 58 84. 5 83. 9 23. 0 17. 04 246. 77 15. 71 6 49 82 73 86 81 97 106 70 61 82 81. 5 78. 7 16. 0 11. 05 273. 79 16. 55

High Protein Beef Cereal Pork Low Protein Beef Cereal Pork

Conclusions • Weight gain is higher for the high protein meat diets • Increasing the level of protein - increases weight gain but only if source of protein is a meat source

Next topic: Numerical Measures of Variability
 Objectives of measures of central tendency
Objectives of measures of central tendency Measures of central tendency median
Measures of central tendency median Measures of central tendency and variation
Measures of central tendency and variation Measures of central tendency
Measures of central tendency Mode in statistics
Mode in statistics Central tendency worksheet
Central tendency worksheet Range in central tendency
Range in central tendency How to do percentile calculation
How to do percentile calculation Measures of central tendency and variation
Measures of central tendency and variation Range of grouped data example
Range of grouped data example Measures of central tendency
Measures of central tendency Measures of central tendency symbols
Measures of central tendency symbols Measures of central tendency symbols
Measures of central tendency symbols Central tendency symbols
Central tendency symbols Lu 분해 예제
Lu 분해 예제 Central tendency of grouped data
Central tendency of grouped data Measures of central tendency notes
Measures of central tendency notes How to calculate mode for grouped data
How to calculate mode for grouped data Objectives of measures of central tendency
Objectives of measures of central tendency Statistics chapter 3 measures of central tendency
Statistics chapter 3 measures of central tendency Advantages of measures of central tendency
Advantages of measures of central tendency Summarion notation
Summarion notation Modus
Modus Central tendency
Central tendency Use of central tendency
Use of central tendency Median for even number
Median for even number Is range part of central tendency
Is range part of central tendency Importance of central tendency
Importance of central tendency Objective of central tendency
Objective of central tendency Central tendency
Central tendency How to get frequency distribution
How to get frequency distribution Fraktil adalah
Fraktil adalah Median rumus
Median rumus Central tendency bias
Central tendency bias Central tendency spss
Central tendency spss How to calculate mode from mean and median
How to calculate mode from mean and median Central tendency symbols
Central tendency symbols Central tendency and variability
Central tendency and variability Central tendency symbols
Central tendency symbols Central tendency and spread homework
Central tendency and spread homework Numerical description
Numerical description Numerical methods of descriptive statistics
Numerical methods of descriptive statistics Jack in the box
Jack in the box Numerical descriptive measures exercises
Numerical descriptive measures exercises Numerical descriptive measures
Numerical descriptive measures How to find mean deviation for grouped data
How to find mean deviation for grouped data Numerical descriptive measures
Numerical descriptive measures Numerical
Numerical Interquartile range formula for ungrouped data
Interquartile range formula for ungrouped data Numerical descriptive measures
Numerical descriptive measures Repeated-measures design
Repeated-measures design The perceptual tendency to group together stimuli
The perceptual tendency to group together stimuli Qg height tendency equation
Qg height tendency equation The societal tendency toward class stratification
The societal tendency toward class stratification Projected cognitive similarity is the tendency to
Projected cognitive similarity is the tendency to Bleeding tendency
Bleeding tendency Tendency to conform
Tendency to conform Get2 test
Get2 test What is the conflict in animal farm
What is the conflict in animal farm Pressure tendency
Pressure tendency Fuel system soak testing
Fuel system soak testing Bleeding tendency
Bleeding tendency Terminal values and instrumental values
Terminal values and instrumental values Diffraction is the tendency of light to:
Diffraction is the tendency of light to: Buoyancy is a tendency
Buoyancy is a tendency Actinide contraction
Actinide contraction Is the tendency to be careful scrupulous and persevering
Is the tendency to be careful scrupulous and persevering Weathervaning tendency is greatest when taxiing
Weathervaning tendency is greatest when taxiing Selfserving bias
Selfserving bias Actualising tendency
Actualising tendency Numerical variable
Numerical variable Counterdiscipline
Counterdiscipline Specific factors model numerical example
Specific factors model numerical example What is a numerical pattern
What is a numerical pattern Mathematical preliminaries in numerical computing
Mathematical preliminaries in numerical computing Numerical methods
Numerical methods Representing numerical data
Representing numerical data Tooth numbers
Tooth numbers Xiaolin wu circle
Xiaolin wu circle Erlanger classification
Erlanger classification Numerical differentiation examples
Numerical differentiation examples What is a numerical expression example
What is a numerical expression example Grometry
Grometry Visual numerical learning style
Visual numerical learning style Modified euler method formula
Modified euler method formula Contoh user requirement
Contoh user requirement Second derivative formula
Second derivative formula Newton backward interpolation formula
Newton backward interpolation formula Numerical stroop
Numerical stroop Relationships between two numerical variables
Relationships between two numerical variables Logo notasi
Logo notasi Numerical method
Numerical method Comparative advantage numerical example
Comparative advantage numerical example Bankers algorithm numerical
Bankers algorithm numerical Birge vieta method examples
Birge vieta method examples Pde project topics
Pde project topics Numerical expression examples
Numerical expression examples Chronicle of higher education
Chronicle of higher education Numerical summary
Numerical summary Genetics
Genetics Numerical calculations
Numerical calculations Numerical geometry of non-rigid shapes
Numerical geometry of non-rigid shapes Relative true error formula
Relative true error formula Graphical and numerical methods
Graphical and numerical methods A parameter is a numerical description of a
A parameter is a numerical description of a Numerical model
Numerical model Numerical optimization techniques for engineering design
Numerical optimization techniques for engineering design Numerical integration of discrete data
Numerical integration of discrete data Characteristic equation
Characteristic equation What is a numerical summary of a sample
What is a numerical summary of a sample Representing numerical data
Representing numerical data Numerical pattern
Numerical pattern Literal coefficient
Literal coefficient Numerical flux
Numerical flux