What is The Error How it is happened

What is The Error ? How it is happened ? 1

Definition • The Error in a computed quantity is defined as: Error = True Value – Approximate Value • Example: - True Value : phi = 3. 14159265358979 - Appr. Value : 22/7 = 3. 14285714 - Error = -0. 00126448926735 2

Kind of Error • The Absolute Error is measure the magnitude of the error • The Relatife Error is a measure of the error in relation to the size of the true value 3

Example • True value : 10 m Appr. Value : 9 m • True value : 1000 m Appr. Value : 999 m 4

Source of Error • Truncation Error – Caused by approximation used in the mathematical formula of the scheme • Round-off Error – Caused by the limited number of digits that represent numbers in a computer and – The ways numbers are stored and additions and substractions are performed in a computer 5

Background of The Truncation Error • Numerical solutions are mostly approximations for exact solution • Most numerical methods are based on approximating function by polynomials • How accurately the polynomial is approximating the true function ? • Comparing the polynomial to the exact solution it becames possible to evaluate the error, called truncation error 6

Taylor Series • The most important polynomials used to derived numerical schemes and analyze truncation errors • With an infinite power series, it is exactly represents a function within a certain radius about a given point 7

Taylor’s Theorem (See Introduction to Real Analysis by Bartle and Sherbert for proves) 8

Applications • For practice we denote • Find the Taylor expansion of sin(x) about answer: 9

• How about the Taylor expansion of Tan(x) at ? • The Taylor expansion of a function about is called the Maclaurin series. Thus, Maclaurin series for sin(x) is, • It is impossible in practical applications to include an infinite number of terms. Therefore, the Taylor series has to be truncated after a certain order term 10

• If the Taylor series is truncated after the N th order term, it is expressed as • Since cannot be found exactly, the error term is often approximated by 11

Example 1: Find the Taylor expansion of about which use the first two, three, four and five and evaluate for x= 0. 5, respectively. Answer: 12

13

Example 2: Find the Taylor expansion of about which use the first two, three, four and five and evaluate for x= 0. 5, respectively. Answer: 14

15

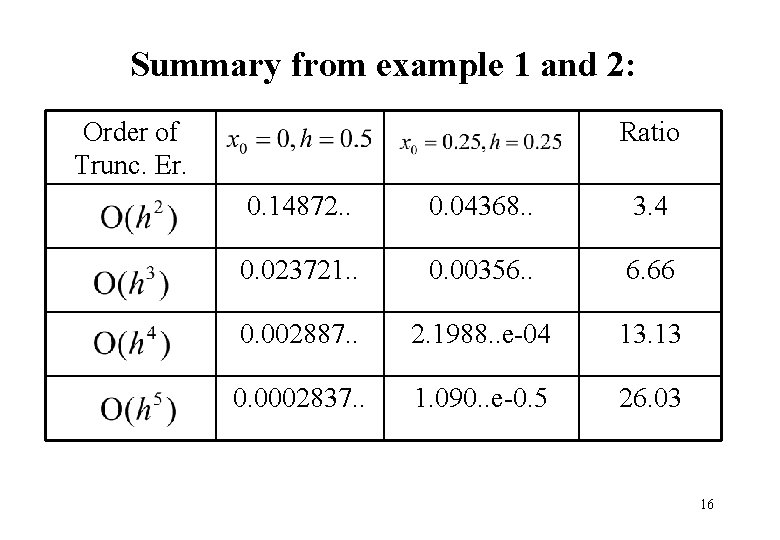
Summary from example 1 and 2: Order of Trunc. Er. Ratio 0. 14872. . 0. 04368. . 3. 4 0. 023721. . 0. 00356. . 6. 66 0. 002887. . 2. 1988. . e-04 13. 13 0. 0002837. . 1. 090. . e-0. 5 26. 03 16

Numbers on Computers • Computers do not use the decimal system in computations and memory but use the binary system • It caused by computer memory consists of a huge number of electronic and magnetic recording devices, of which each element has only “on” and “off” statuses 17

• Example: In a single precision, 4 bytes, or equivalently 32 bits, are used to store one real number. If a decimal number is given by input, it first converted to the closest binary in the normalized format: where a is always 1 and b’s are binary digit that are 0 or 1; z is an exponent which is also expressed in binary. 18

Numbers Store in Computer’s Memory for Single Precision (IBM 370) where s is as sign (+ or -), e is an exponent, and m is a mantissa including the a and b’s. Example: 19

Causes Round-off Error The summation of these two numbers becomes Because the mantissa has 24 bits, therefore, the result of this calculation is stored in memory as Thus, whenever 0. 00001 is added to 1. 5, the result gains 0. 0000000136 as an error which called round 20 off error

The effects of round-off error can be minimized by changing the computational algorithm although it must be devised case by case. Some useful strategies include: o Double precision o Grouping o Taylor expansions o Changing definition of variables o Rewriting the equation to avoid substraction 21

• Double Precision (IBM 370) In a double precision, 8 bytes, or equivalently 64 bits, are used to store one real number. In this format 1 bit is used for sign, 7 bits are used for exponent, and 56 bits are used for mantissa. • Grouping when the small numbers are computed, e. g. addition, substraction, etc. , grouping them helps to reduce round-off errors. For example, to add 0. 00001 to unity ten thousand times one can grouped into 100 groups and each group consists of 100 small values. 22

• Taylor Expansions as approaches 0, accuracy of a numerical evaluation for becomes very poor because round-off errors. By using Taylor expansion, we can rewrite the equation so that the accuracy for is improved as 23

• Rewriting the equation to avoid substraction consider the equation of for an increasing of values x, the calculation of the equation above has a loss-of-significance error. To avoid this error one can reformulate it to get 24