Ukuran Tendensi Sentral Nilai RataRata Median Modus mode

Ukuran Tendensi Sentral Nilai Rata-Rata, Median, Modus (mode)

Tendensi Sentral?

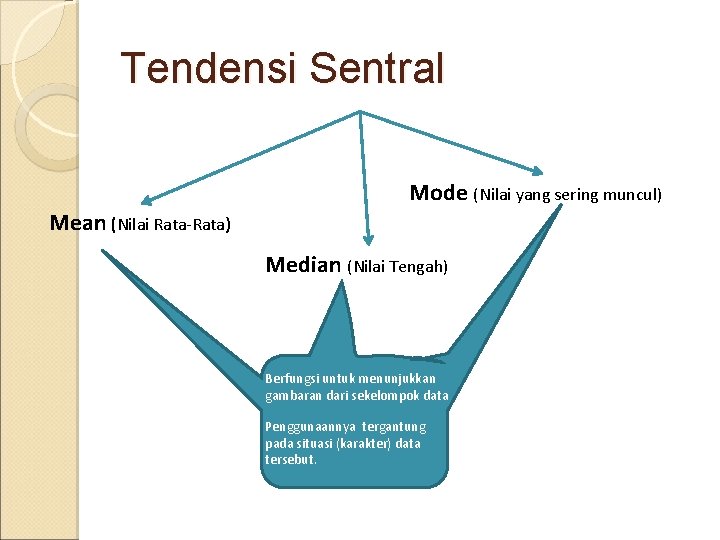
Tendensi Sentral Mode (Nilai yang sering muncul) Mean (Nilai Rata-Rata) Median (Nilai Tengah) Berfungsi untuk menunjukkan gambaran dari sekelompok data Penggunaannya tergantung pada situasi (karakter) data tersebut.

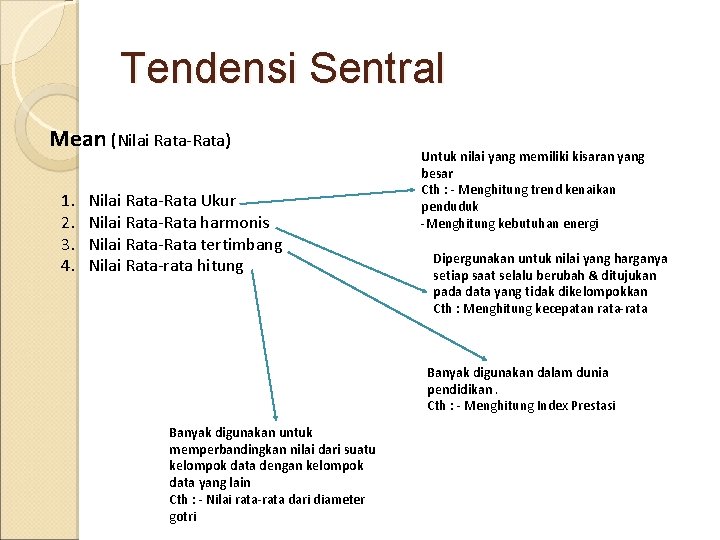
Tendensi Sentral Mean (Nilai Rata-Rata) 1. 2. 3. 4. Nilai Rata-Rata Ukur Nilai Rata-Rata harmonis Nilai Rata-Rata tertimbang Nilai Rata-rata hitung Untuk nilai yang memiliki kisaran yang besar Cth : - Menghitung trend kenaikan penduduk -Menghitung kebutuhan energi Dipergunakan untuk nilai yang harganya setiap saat selalu berubah & ditujukan pada data yang tidak dikelompokkan Cth : Menghitung kecepatan rata-rata Banyak digunakan dalam dunia pendidikan. Cth : - Menghitung Index Prestasi Banyak digunakan untuk memperbandingkan nilai dari suatu kelompok data dengan kelompok data yang lain Cth : - Nilai rata-rata dari diameter gotri

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata ukur (U)

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata ukur (U) Contoh 1 : Hitunglah rata-rata ukur dari data berikut ini : 10 ; 15 ; 16 ; 25 Penyelesaian : atau U = 15, 6508

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata ukur (U) Contoh 2: Titik Tengah 5 10 15 20 25 Σ Frekuensi 4 2 8 3 U = 13, 0945 1 18 Tentukan harga rata-rata dari data disamping :

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata ukur (U) Contoh 3: Cari kenaikan rata-rata pertahun dari tabel jumlah total tengah listrik yang dibangkitkan antara tahun 1954 – 1961 Cara 2 U = 1, 0372 Dari kedua jawaban tersebut kemudian dikalikan dengan 100% dan dikurangi 100 maka pertumbuhan relatif tercapai pada kisaran 3, 72 % 4, 04% perbedaan nilai ini terjadi dikarenakan proses pembulatan angka U = 1, 0404

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata Hermonis (H)

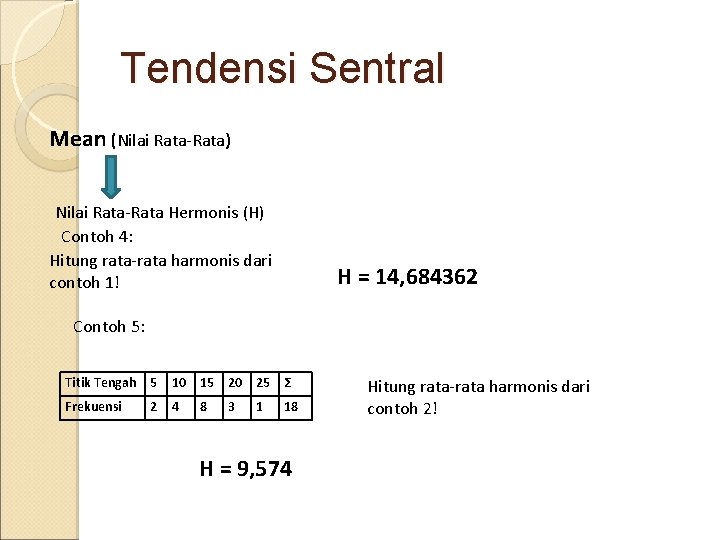
Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata Hermonis (H) Contoh 4: Hitung rata-rata harmonis dari contoh 1! H = 14, 684362 Contoh 5: Titik Tengah 5 10 15 20 25 Σ Frekuensi 4 2 8 3 1 18 H = 9, 574 Hitung rata-rata harmonis dari contoh 2!

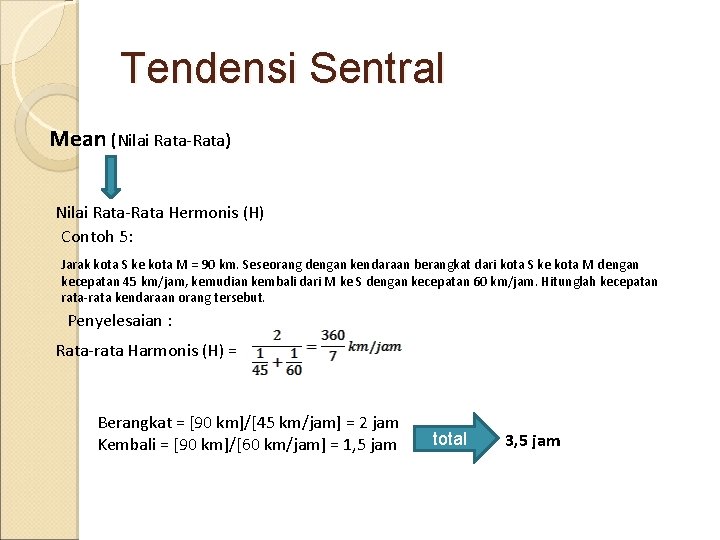
Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata Hermonis (H) Contoh 5: Jarak kota S ke kota M = 90 km. Seseorang dengan kendaraan berangkat dari kota S ke kota M dengan kecepatan 45 km/jam, kemudian kembali dari M ke S dengan kecepatan 60 km/jam. Hitunglah kecepatan rata-rata kendaraan orang tersebut. Penyelesaian : Rata-rata Harmonis (H) = Berangkat = [90 km]/[45 km/jam] = 2 jam Kembali = [90 km]/[60 km/jam] = 1, 5 jam total 3, 5 jam

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata Hitung

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata Hitung Contoh 6: Berikut ditunjukkan tabel distribusi dari muatan maksimum yang dapat ditahan oleh suatu jenis kabel yang dihasilkan oleh suatu pabrik kabel tertentu : Max. Load (ton) 9, 3 – 9, 7 9, 8 – 10, 2 10, 3 – 10, 7 10, 8 – 11, 2 11, 3 – 11, 7 11, 8 – 12, 2 12, 3 – 12, 7 12, 8 – 13, 2 Number of Cable 2 5 12 17 14 6 3 1 Hitunglah nilai rata-rata kekuatan kabel tersebut

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata Hitung Contoh 6: Dari tabel distribusi yang di ada dapat dibuat tabel sebagai berikut : Nilai rata-rata :

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata Hitung Contoh enam dapat dikerjakan dengan cara lain, yaitu metode computing origin Untuk data yang tidak dikelompokkan Untuk data yang dikelompokkan A = Nilai sembarang yang diambil

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata Hitung Contoh 7: Hitung nilai rata-rata dari data contoh soal nomor 6 Pertama menentukan nilai A = 11; maka didapat tabel frekuensi sbb : Maka nilai rata-ratanya : (dalam ton)

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata Hitung Selain metode computing origin, untuk menyelesaikan conto soal nomor 6 dapat juga menggunakan metode Coding methode Yaitu suatu cara dengan memberikan kode pada masing kelas. A= titik tengah dari sembarang data Pemberian angka / kode sesuai denan jumlah data.

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata Hitung Sehingga didapatkan Dimana : X =Nilai rata-rata A = Titik tengah = titik asal baru n = Jumlah data Ui=Kode ke-I C = interval K = Jumlah kelas fi = Frekuensi kelas ke i

Tendensi Sentral Mean (Nilai Rata-Rata) Nilai Rata-Rata Hitung Contoh 8: Hitung rata-rata dari contoh soal nomor 7 dengan cara coding system Dari tabel disamping didapat nilai rata-ratanya : Nilai rerata = A + CU A = 11 C = 0, 5

Tendensi Sentral Median (Nilai Tengah) Yaitu nilai yang membagi dua dari suatu urutan data sehingga banyaknya pengamatan dari masing -masing bagian tersebut sama 1. Menentukan median dari data yang dikelompokkan -Nilai median terletak pada data ke 30, yaitu di kelas yang ke III -Data ke 30 terletak pada urutan ke 15 pada kelas yang ke III -Nilai ke 15 tidak diketahui maka dicari dengan interpolasi Median = 0, 7315 + (15/20). (0, 004) = 0, 7345

Tendensi Sentral Median (Nilai Tengah) Dari penjelasan sebelumnya maka didapatkan hubungan secara matematis Dimana : Li = batas tepi kelas median n = jumlah data Σfi = jumlah sebelum kelas median fm = frekuensi kelas median C = Interval kelas

Tendensi Sentral 2. Menentukan median dengan cara grafis a. Dengan menggunakan Ogive PT : PQ = ST : QR PT : 0, 004 = (50 -25) : (58, 33 -25) PT : 0, 004 = 25 : 28, 33 PT = (25 x 0, 004) / 28, 33 = 0, 003

Tendensi Sentral a. Dengan menggunakan Histogram Dimana : LCB = Lower Class Boundaries (batas tepi bawah) L = Luas total seluruh histogram Σfi = Total frekuensi sebelum luasan histogram dimana median terletak C = Interval Fm = frekuensi kelas median

Tendensi Sentral Mode (Modus) a. Mode data yang tidak dikelompokkan b. Mode data yang dikelompokkan Dimana : Li = Batas tepi bawah kelas mode Δ 1 = Selisih antara frekuensi didalam kelas mode dengan frekuensi kelas yang mendahuluinya. Δ 2 = Selisih antara frekuensi kelas mode dengan frekuensi dari kelas berikutnya. C = Interval Kelas.

Tendensi Sentral Mode (Modus) Contoh 6: Nilai mode distribusi dari data disamping adalah?

Tendensi Sentral Mode (Modus) c. Mencari mode dengan cara grafik OS 1 + S 1 T 1 = 0, 7315 + S 1 T 1 = UT UT : TV = PS : QR UT : TV = (20 -10) : (20 -14) = 10 : 6 UT + TV = Interval = 0, 004 UT = (10/16) x 0, 004 = 0, 0025 Mode = 0, 7135 + 0, 0025 = 0, 7340