UKURAN PEMUSATAN Nilai ratarata Modus dan Median sumedana

UKURAN PEMUSATAN • Nilai rata-rata • Modus dan Median sumedana 12@yahoo. com 1

NILAI RATA-RATA A. Rata-rata hitung untuk data tak berbobot. sumedana 12@yahoo. com 2

• untuk data berbobot, lihat contoh berikut x f f. x 10 2 20 15 2 30 20 4 80 25 6 150 30 4 120 35 3 105 21 505 sumedana 12@yahoo. com 3

MENGHITUNG NILAI RATA-RATA DARI DATAkelas” TERKELOMPOK • Dengan cara “tanda No urut Kelas Interval Frekuensi Tanda kelas f. x f x 40 50 1 2 35, 5 45, 5 35, 5 91 - 60 - 70 - 80 - 90 - 100 5 15 25 20 12 55, 5 65, 5 75, 5 85, 5 95, 5 278 983 1888 1710 1146 80 6130 1 2 31 41 - 3 4 5 6 7 51 61 71 81 91 sumedana 12@yahoo. com 4

• Dengan cara “rata-rata duga (AM)” No urut 1 2 3 4 5 6 7 Kelas Interval 31 41 51 61 71 81 91 - 40 50 60 70 80 90 100 sumedana 12@yahoo. com Frekuensi f 1 2 5 15 25 20 12 80 d f. d -4 -3 -2 -1 0 1 2 -4 -6 -10 -15 0 20 24 9 5

B. Nilai rata-rata ukur (U) jika terdapat beberapa nilai data yang seolah membentuk deret geometri dan berlaku hubungan maka banyak digunakan untuk data teknik atau yang bersifat enginering sumedana 12@yahoo. com 6

contoh • Hitung nilai rata-rata dari data berikut 560, 8, 33, 136, 17, 67, 275 Setelah disusun : 8, 17, 33, 67, 136, 275, 560 Perhatikan : 17 33 67 136 275 560 8 17 33 67 136 275 sumedana 12@yahoo. com 7

C. Nilai rata-rata harmonis sumedana 12@yahoo. com 8

D. Nilai rata-rata kuadratis (NRK) dari kumpulan bilangan yang merupakan urutan maka NRK banyak digunakan dalam ilmu fisika atau teknik yg banyak hubungannya dengan fisika sumedana 12@yahoo. com 9

MODUS • Gejala dengan frekuensi tertinggi • Gejala yang paling sering muncul sumedana 12@yahoo. com 10

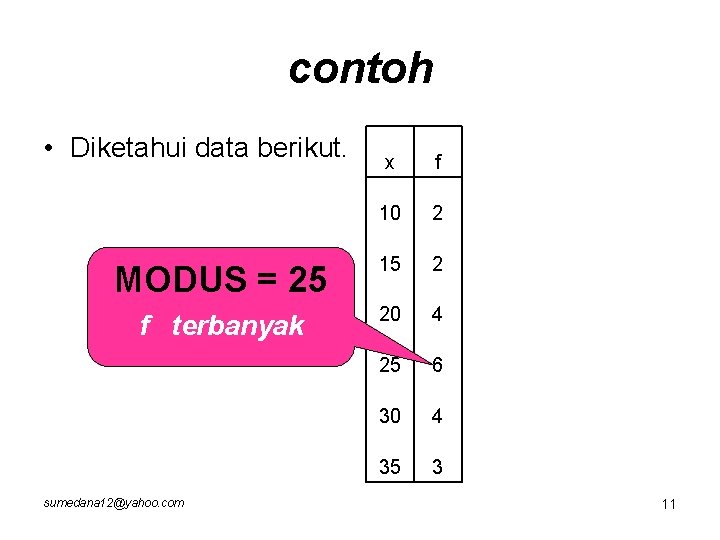
contoh • Diketahui data berikut. MODUS = 25 f terbanyak sumedana 12@yahoo. com x f 10 2 15 2 20 4 25 6 30 4 35 3 11

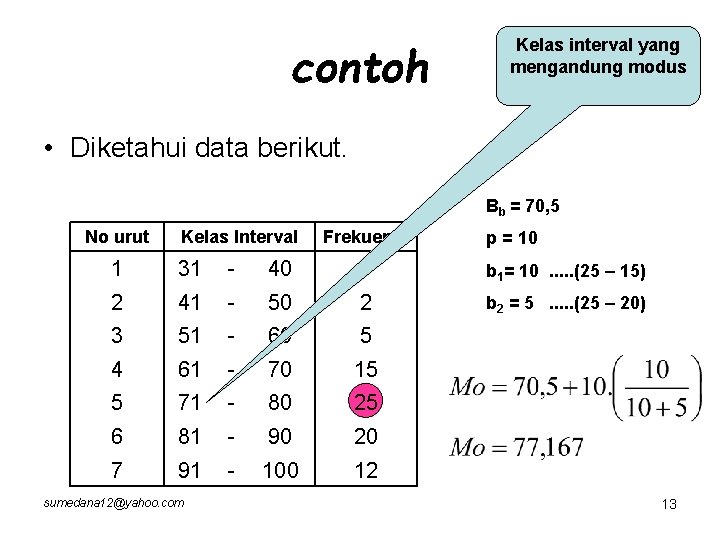
MODUS UNTUK DATA TERKELOMPOK • Dihitung dengan rumus : Mo = modus Bb = batas bawah kelas yg mengandung modus p = panjang kelas interval b 1 = selisih frekuensi yg mengandung modus dengan frekuensi sebelumnya sumedana 12@yahoo. com b 2 = selisih frekuensi yg mengandung modus dengan frekuensi sesudahnya 12

contoh Kelas interval yang mengandung modus • Diketahui data berikut. Bb = 70, 5 No urut Kelas Interval Frekuensi p = 10 1 31 - 40 1 b 1= 10 . . . (25 – 15) 2 41 - 50 2 b 2 = 5 . . . (25 – 20) 3 51 - 60 5 4 61 - 70 15 5 71 - 80 25 6 81 - 90 20 7 91 - 100 12 sumedana 12@yahoo. com 13

MEDIAN • data yang terletak di tengah-tengah setelah data itu disusun menurutan nilainya sehingga membagi dua sama besar sumedana 12@yahoo. com 14

• median = 65 mengandung makna bahwa separo data bernilai kurang dari atau sama dengan 65 dan separonya lagi bernilai sama dengan atau lebih dari 65 sumedana 12@yahoo. com 15

contoh • diketahui data berikut : median ada di antara 5 dan 6. median = (5+6)/2 = 5, 5 2, 3, 3, 6, 9, 12, 4, 5, 6, 14 carilah median. • sebelum ditentukan, data disusun dulu sesuai urutannya 2, 3, 3, 4, 5, 6, 6, 9, 12, 14 sumedana 12@yahoo. com 16

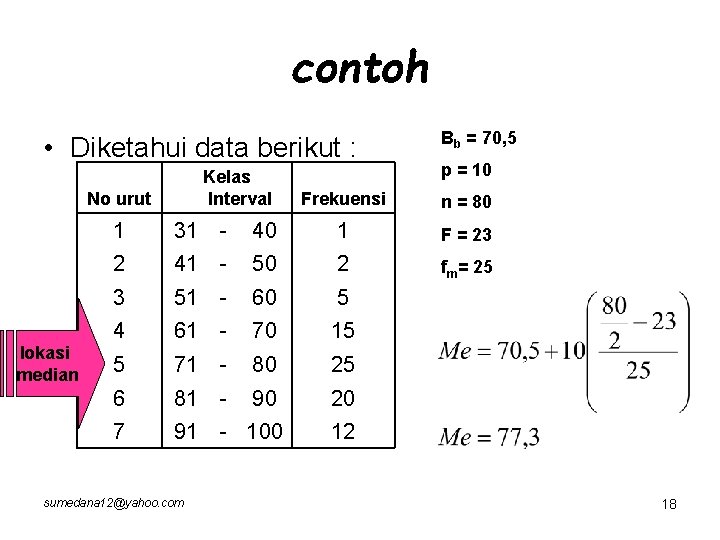
MEDIAN UNTUK DATA TERKELOMPOK • Dihitung dengan rumus : Me = median Bb = batas bawah kelas yg mengandung median p = panjang kelas interval n = banyaknya data (frekuensi) F = frekuensi kumulatif sebelum kelas interval yang mengandung median fm = frekuensi kelas interval yang mengandung median sumedana 12@yahoo. com 17

contoh • Diketahui data berikut : Kelas Interval No urut lokasi median Bb = 70, 5 p = 10 Frekuensi n = 80 1 31 - 40 1 F = 23 2 41 - 50 2 fm= 25 3 51 - 60 5 4 61 - 70 15 5 71 - 80 25 6 81 - 90 20 7 91 - 100 12 sumedana 12@yahoo. com 18

HUBUNGAN EMPIRIS ANTARA RATA-RATA, MEDIAN DAN MODUS • Hubungan empiris yang dapat diandalkan Modus + 2. Rata-rata = 3. Median sumedana 12@yahoo. com 19

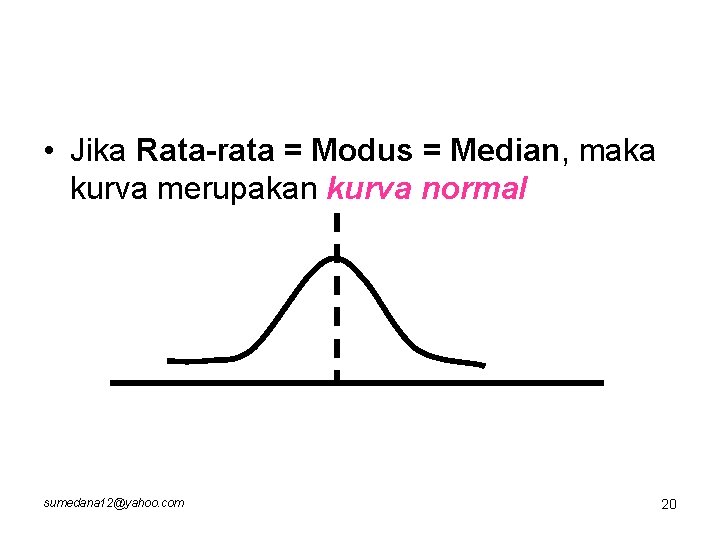
• Jika Rata-rata = Modus = Median, maka kurva merupakan kurva normal sumedana 12@yahoo. com 20

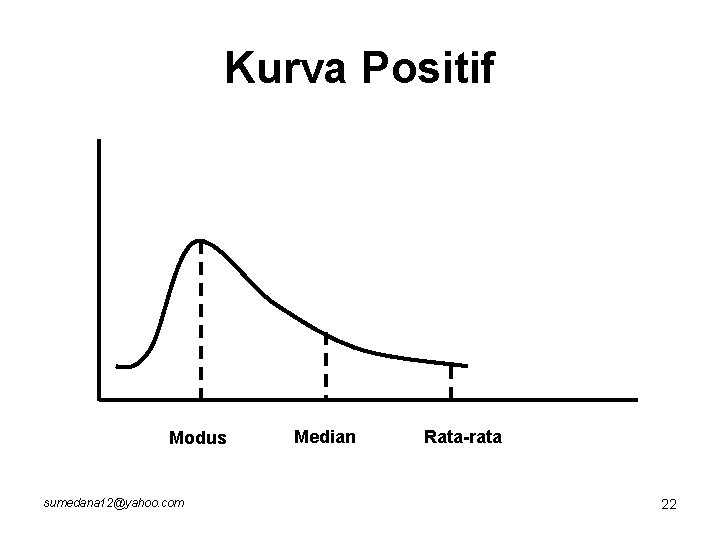
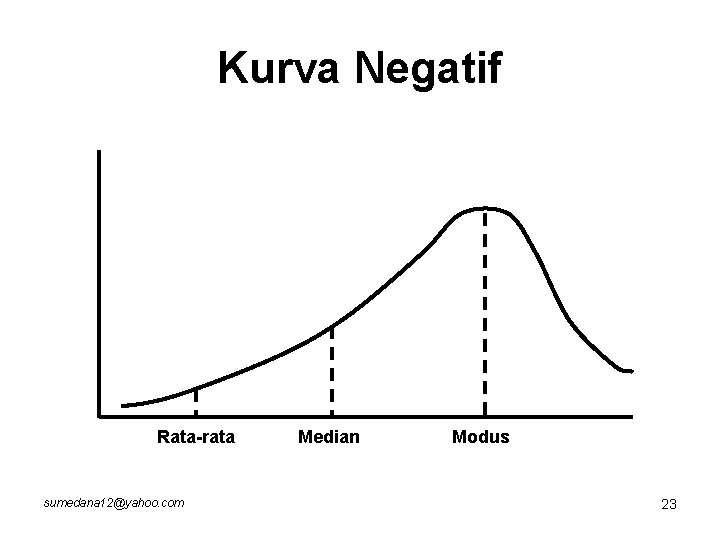
• Jika Rata-rata ≠ Modus ≠ Median, maka kurva mungkin positif dan mungkin juga negatif sumedana 12@yahoo. com 21

Kurva Positif Modus sumedana 12@yahoo. com Median Rata-rata 22

Kurva Negatif Rata-rata sumedana 12@yahoo. com Median Modus 23