UKURAN PENYEBARAN DATA UKURAN PENYEBARAN DATA Ukuran penyebaran

UKURAN PENYEBARAN DATA

UKURAN PENYEBARAN DATA Ukuran penyebaran data adalah suatu ukuran yang menyatakan seberapa besar nilai-nilai data berbeda atau bervariasi dengan nilai ukuran pusatnya atau seberapa besar penyimpangan nilai-nilai data dengan nilai pusatnya. 1. Jangkauan ( Range ) Jangkauan adalah selisih antara nilai maksimum dan nilai minimum yang terdapat dalam data. Jangkauan dapat dihitung dengan rumus: R = X maks – X min Contoh : Tentukan range dari data : 10, 6, 8, 2, 4 Jawab : R = Xmaks – Xmin = 10 – 2 = 8 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA 2. Simpangan Rata-rata Simpangan rata-rata dari sekumpulan bilangan adalah: nilai rata-rata hitung harga mutlak simpangan-simpangannya. a. Data tunggal SR = Contoh : Nilai ulangan matamatika dari 6 siswa adalah : 7, 5, 6, 3, 8, 7. Tentukan simpangan rata-ratanya! Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Jawab: = = 6 SR = = = Hal. : 1, 33 STATISTIK Adaptif

UKURAN PENYEBARAN DATA b. Data berbobot / data kelompok SR = x = data ke-i (data berbobot ) = titik tengah kelas interval ke-i (data kelompok ) f = frekuensi Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Contoh : Tentukan simpangan rata-rata dari data berikut : Hal. : Data Frekwensi x 3– 5 2 4 6– 8 4 7 9 – 11 8 10 12 - 14 6 13 Jumlah 20 STATISTIK Adaptif

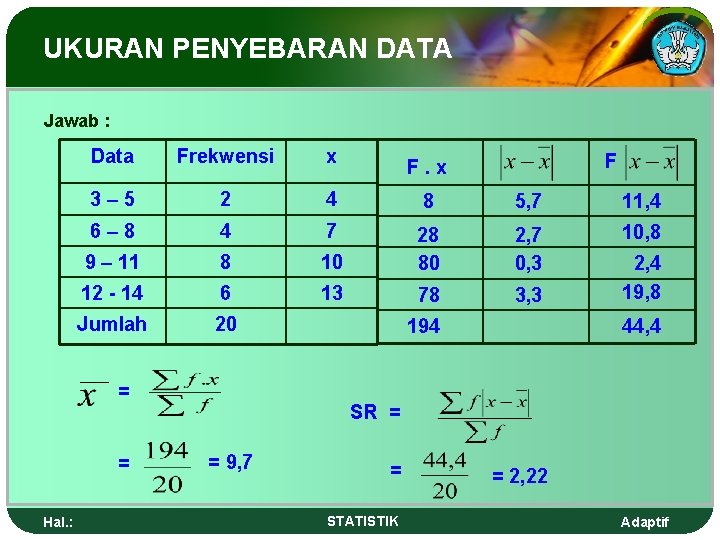
UKURAN PENYEBARAN DATA Jawab : Data Frekwensi x 3– 5 2 4 8 5, 7 11, 4 6– 8 4 7 8 10 2, 7 0, 3 10, 8 9 – 11 28 80 12 - 14 6 13 78 3, 3 Jumlah 20 = = Hal. : F F. x 194 2, 4 19, 8 44, 4 SR = = 9, 7 = STATISTIK = 2, 22 Adaptif

UKURAN PENYEBARAN 3. Simpangan Baku / standar deviasi Simpangan Baku (S) dari sekumpulan bilangan adalah akar dari jumlah deviasi kuadrat dari bilangan-bilangan tersebut dibagi dengan banyaknya bilangan atau akar dari rata-rata deviasi kuadrat. a. Data Tunggal S = atau S = Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Contoh : Tentukan simpangan baku dari data : 2, 3, 5, 8, 7. x Jawab : = =5 S = = 2 -3 9 3 -2 4 5 0 0 8 3 9 7 2 4 26 = Hal. : STATISTIK Adaptif

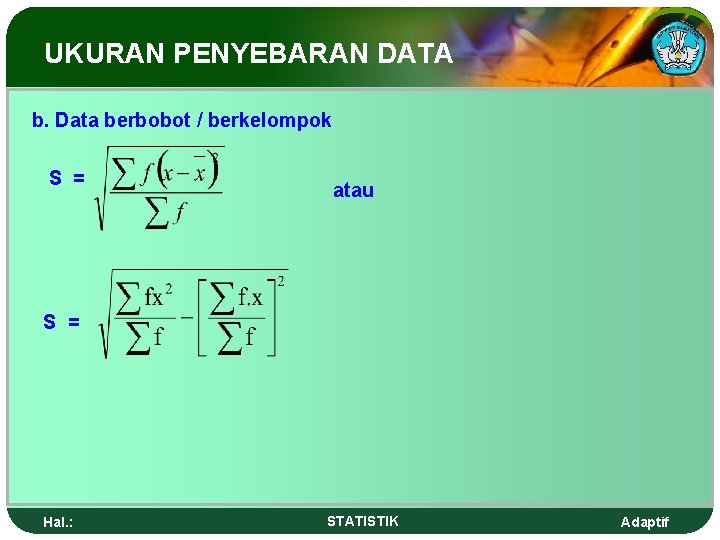
UKURAN PENYEBARAN DATA b. Data berbobot / berkelompok S = atau S = Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Contoh: Tentukan standar deviasi dari data berikut Hal. : Data Frekw x 3– 5 2 4 6– 8 4 7 9 – 11 8 10 12 - 14 6 13 Jumlah 20 STATISTIK Adaptif

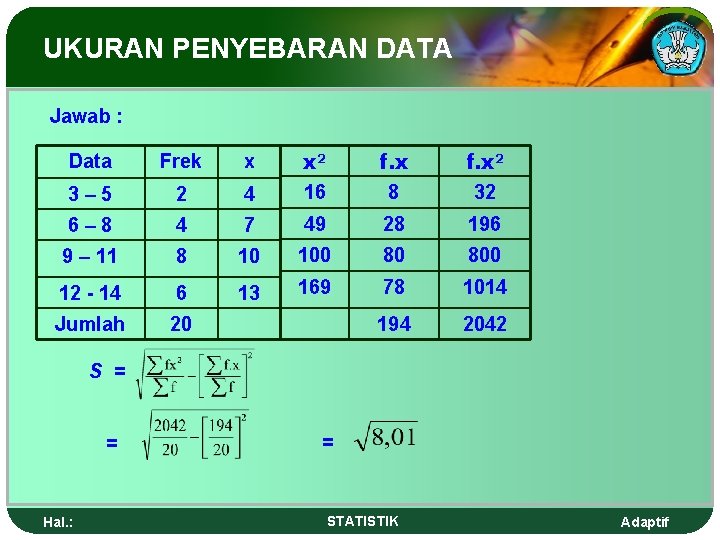
UKURAN PENYEBARAN DATA Jawab : Data Frek x x 2 f. x 2 3– 5 2 4 16 8 32 6– 8 4 7 49 28 196 9 – 11 8 10 100 80 800 12 - 14 6 13 169 78 1014 Jumlah 20 194 2042 S = = Hal. : = STATISTIK Adaptif

UKURAN PENYEBARAN DATA 4. Kuartil adalah nilai yang membagi kelompok data atas empat bagian yang sama setelah bilangan-bilangan itu diurutkan. Dengan garis bilangan letak kuartil dapat ditunjukkan sebagai berikut: Q 1 Q 2 Q 3 Menentukan nilai Kuartil a. Data tunggal b. Letak Qi = data ke c. dengan i = 1, 2, 3 Hal. : dan n = banyaknya data STATISTIK Adaptif

UKURAN PENYEBARAN DATA Contoh : Hasil pendataan usia, dari 12 anak balita (dalam tahun) diketahui sebagai berikut : 4, 3, 4, 4, 2, 1, 1, 2, 1, 3, 3, 4 , tentukan : a. Kuartil bawah (Q 1) b. Kuartil tengah (Q 2) c. Kuartil atas (Q 3) Jawab : Data diurutkan : 1, 1, 1, 2, 2, 3, 3, 3, 4, 4 a. Letak Q 1 = data ke – = data ke- 3 ¼ Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Nilai Q 1 = data ke-3 + ¼ (data ke 4 – data ke 3) = 1 + ¼ (2 – 1) = 1¼ b. Letak Q 2 = data ke 6½ Nilai Q 2 = data ke 6 + ½ (data ke 7 – data ke 6) = 3 + ½ (3 – 3) = 3 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA c. Letak Q 3 = data ke 9 ¾ Nilai Q 3 = data ke 9 + ¾ (data ke 10 - data ke 9) = 4 + ¾ (4 – 4) = 4 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Jangkauan Semi Inter Kuartil /Simpangan Kuartil (Qd) didefinisikan sebagai berikut: Qd = ½ (Q 3 – Q 1) b. Data Kelompok Nilai Qi = b + p dengan i = 1, 2, 3 b = tepi bawah kelas Qi p = panjang kelas F = jumlah frekuensi sebelum kelas Qi f = frekuensi kelas Qi n = jumlah data Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Contoh : Tentukan simpangan kuartil dari data : Nilai 45 -49 50 -54 55 -59 60 -64 65 -69 70 -74 f 3 6 10 12 5 4 Jumlah 40 Hal. : Jawab : Untuk menentukan Q 1 kita perlu = ¼ x 40 data atau 10 data, jadi Q 1 terletak pada kelas interval ke 3. Dengan b = 54, 5 ; p = 5; F = 9; f = 10 Nilai Q 1 = 54, 5 + 5 = 54, 5 + 0, 5 = 55 STATISTIK Adaptif

UKURAN PENYEBARAN DATA Untuk menetukan Q 3 diperlukan = ¾ x 40 data atau 30 data, jadi Q 3 terletak pada kelas interval ke-4, dengan b = 59, 5; p = 5; F = 19 ; f = 12 Nilai Q 3 = 59, 5 + 5 = 59, 5 + 4, 58 = 64, 08 Jadi, jangkauan semi interkuartil atau simpangan kuartil dari data di atas adalah Qd = ½ (Q 3 –Q 1) = ½ (64, 08 – 55) = 4, 54 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA 5. Persentil dari sekumpulan bilangan adalah nilai yang membagi kelompok bilangan tersebut atas 100 bagian yang sama banyaknya setelah bilangan tersebut diurutkan dari yang terkecil sampai yang terbesar. a. Data tunggal / berbobot Letak Pi = data ke dengan i = 1, 2, …, 99 Contoh : Diketahui data : 9, 3, 8, 4, 5, 6, 8, 7, 5, 7 Tentukan P 20 dan P 70 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Jawab : Data diurutkan : 3 , 4, 5, 5, 6, 7, 7 , 8, 8, 9 Letak P 20 = data ke Nilai P 20 = data ke 2 + = 4+ = data ke 2 (data ke 3 – data ke 2) (5 – 4) =4 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Letak P 70 = data ke 7 Nilai P 70 = data ke 7 + =7+ (data ke 8 - data ke 7) (8– 7) =7 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN b. Data kelompok Nilai Pi = b + p , dengan i = 1, 2, . . , 99 Jangkauan Persentil = P 90 – P 10 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Contoh : Tentukan Jangkauan persentil dari data berikut : Nilai F Hal. : 50 - 59 60 - 69 70 - 79 80 - 89 90 - 99 7 10 15 12 6 Jumlah 50 STATISTIK Adaptif

UKURAN PENYEBARAN DATA Jawab : Untuk menentukan P 10 diperlukan = x 50 data = 5 data, artinya P 10 terletak pada kelas interval pertama dengan b = 49, 5 ; p = 10 ; F =0 ; f = 7 Nilai P 10 = 49, 5 + 7, 14 = 56, 64 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Untuk menetukan P 90 diperlukan = x 50 data = 45 data, artinya P 90 terletak pada kelas interval ke 5, dengan b = 89, 5; F = 44; f = 6. Nilai P 90 = 89, 5 + 1, 67 = 91, 17 Jangkauan Persentil = P 90 – P 10 = 91, 17 – 56, 64 = 34, 53 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Latihan: 1. Nilai tes matematika dari 5 orang siswa adalah sebagai berikut : 7, 6, 7, 8, 7 besarnya simpangan rata-rata dari data tesebut adalah…. Jawab : x = 7 6 7 8 7 0 1 0 Jml 2 Hal. : =7 SR = = = 0, 4 STATISTIK Adaptif

UKURAN PENYEBARAN DATA 2. Standar deviasi (simpangan baku) dari data 4, 6, 7, 6, 3, 4 adalah… Jawab : x = = 5 S = = 4 6 7 6 3 4 Jml (x - ) -1 1 2 1 -2 -1 (x- )2 1 1 4 1 12 = Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA 3. Hasil tes penerimaan pegawai baru suatu perusahaan tercatat sebagai berikut : Nilai Frekuensi 30 -39 40 -49 50 -59 60 -69 70 -79 80 -89 90 -99 3 8 10 20 18 14 7 Hal. : Jika perusahaan akan menerima 75% dari pendaftar yang mengikuti tes tersebut, berapakah nilai minimum yang dapat diterima? STATISTIK Adaptif

UKURAN PENYEBARAN DATA Jawab : Q 1 75% Untuk menentukan Q 1 diperlukan ¼ x 80 data = 20 data, artinya Q 1 terletak pada kelas interval ke 3, dengan b = 49, 5; p = 10; F = 11; f = 10; Nilai Q 1 = 49, 5 + 10 = 58, 5 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA 4. Hasil ulangan program Teknologi Industri dari 50 siswa kelas III pada salah satu SMK adalah sebagai berikut: Nilai F 50 -59 60 -69 70 -79 80 -89 90 -99 7 10 15 12 6 Tentukan nilai P 40 dari data tersebut! Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Jawab: Untuk menentukan P 40 diperlukan = x 50 data atau 20 data, artinya P 40 terletak pada kelas interval ketiga, dengan b = 69, 5 ; p = 10 ; F = 17 dan f = 15. Nilai P 40 = 69, 5 + 10 = 72, 5 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA 5. Hasil tes pelajaran Matematika 15 orang siswa adalah sebagai berikut : 30, 45, 50, 55, 50, 60, 65, 85, 70, 75, 55, 60, 35, 30. Jangkauan semi interkuartil (Qd) dari data di atas adalah…. . Jawab : Data diurutkan : 30, 35, 45, 50, 55, 60, 60, 65, 70, 75, 85. Letak Q 1 = data ke-4 Nilai Q 1 = data ke-4 = 45 Letak Q 3 = data ke-12 Nilai Q 3 = data ke 12 = 65 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Jangkauan semi interkuartil (Qd) = ½ ( Q 3 – Q 1 ) = ½ ( 65 – 45 ) = 10 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA 6. Koefisien Variasi Koefisien variasi adalah perbandingan antara simpangan standar dengan nilai rata-rata yang dinyatakan dengan persentase. Koefisien variasi berguna untuk melihat sebaran data dari rata-rata hitungnya. Besarnya Koefisien Variasi dinyatakan dengan rumus, KV = x 100% KV = koefisien variasi S = simpangan standar = rata-rata Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Contoh 1: Nilai rata-rata matematika Kelas III Mesin 1 adalah 80 dengan simpangan standar 4, 5. Jika nilai rata-rata Kelas III Mesin 2 adalah 70 dengan simpangan standar 5, 2. Hitunglah koefisien variasi masing-masing. Jawab : KV III Mesin 1 = x 100% = 5, 6% KV III Mesin 2 = x 100% = 7, 4% Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Contoh 2 : Standar deviasi sekelompok data adalah 1, 5 sedang koefisien variasinya adalah 12, 5%. Mean kelompok data tersebut adalah…. Jawab : KV = x 100% 12, 5% = x 100% = = 12 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA 7. Angka Baku digunakan untuk mengetahui kedudukan suatu objek yang sedang diselidiki dibandingkan terhadap nilai rata-rata kumpulan objek tersebut. Angka Baku (nilai standar) dapat dihitung dengan menggunakan rumus : Z = x = nilai data = nilai rata-rata s = standar deviasi Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Contoh 1: Seorang siswa mendapat nilai matematika 70 dengan rata-rata 60 dan standar deviasi 12, nilai Bahasa Inggris 80 dengan rata 75 dan simpangan standarnya 15, manakah kedudukan nilai yang paling baik ? Jawab : Zm = = 0, 83 Zb = = 0, 33 Jadi kedudukan nilai matematika lebih baik dari pada nilai Bahasa Inggris. Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Contoh 2 : Rata-rata dan simpangan standar upah pesuruh kantor masing-masing adalah Rp 65. 000, 00 dan Rp 1. 500, 00. Jika Pak Darmawan salah seorang pesuruh yang upahnya Rp 67. 250, 00, nilai standar upah Pak Darmawan adalah…. Jawab : Z= = 1, 5 Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Ukuran Keruncingan / kurtosis Kurtosis adalah derajat kelancipan suatu distribusi jika dibandingkan dengan Distribusi normal Untuk menghitung tingkat keruncingan suatu kurva (koefisien kurtosis) dapat Digunakan rumus : KK = Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Keterangan : Jika nilai KK > 3 kurva leptokurtis (puncaknya runcing sekali) KK < 3 kurva platikurtis (puncaknya agak mendatar) KK = 0 kurva mesokurtis (puncaknya tidak begitu runcing atau distribusi normal) Contoh : Dari sekelompok data yang disusun dalam tabel distribusi frekuensi diketahui nilai Q 1 = 55, 24 ; Q 3 = 73, 64 ; P 10 = 44, 5 ; P 90 = 82, 5. Besarnya koefisien kurtosis kurva data tersebut adalah…. Hal. : STATISTIK Adaptif

UKURAN PENYEBARAN DATA Jawab : KK = = = 0, 242 Karena KK < 3 maka kurva distribusi tersebut platikurtik. Hal. : STATISTIK Adaptif