UKURAN PEMUSATAN DATA UKURAN PEMUSATAN Merupakan nilai tunggal

UKURAN PEMUSATAN DATA

UKURAN PEMUSATAN Merupakan nilai tunggal yang mewakili semua data atau kumpulan pengamatan dimana nilai tersebut menunjukkan pusat data. Yang termasuk ukuran pemusatan : 1. Rata-rata hitung 2. Median 3. Modus 4. Rata-rata ukur 5. Rata-rata harmonis

1. RATA-RATA HITUNG Rumus umumnya : 1. Untuk data yang tidak mengulang 2. Untuk data yang mengulang dengan frekuensi tertentu

RATA-RATA HITUNG (lanjutan) 1. Dalam Tabel Distribusi Frekuensi Interval Kelas Nilai Tengah (X) Frekuensi f. X 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 15 28 41 54 67 80 93 3 4 4 8 12 23 6 45 112 164 432 804 1840 558 Σf = 60 Σf. X = 3955

RATA-RATA HITUNG (lanjutan) 2. Dengan Memakai Kode (U) Interval Kelas Nilai Tengah (X) U Frekuensi f. U 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 15 28 41 54 67 80 93 -3 -2 -1 0 1 2 3 3 4 4 8 12 23 6 -9 -8 -4 0 12 46 18 Σf = 60 Σf. U = 55

RATA-RATA HITUNG (lanjutan) 3. Dengan pembobotan Masing-masing data diberi bobot. Misal A memperoleh nilai 65 untuk tugas, 76 untuk mid dan 70 untuk ujian akhir. Bila nilai tugas diberi bobot 2, Mid 3 dan Ujian Akhir 4, maka rata-rata hitungnya adalah :

2. MEDIAN

2. MEDIAN Untuk data berkelompok

2. MEDIAN (lanjutan) Contoh : Interval Kelas Frekuensi 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 3 4 4 8 12 23 6 Σf = 60 Letak median ada pada data ke 30, yaitu pada interval 6173, sehingga : L 0 = 60, 5 F = 19 f = 12

3. MODUS Untuk data berkelompok

3. MODUS (lanjutan) Contoh : Interval Kelas Frekuensi 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 3 4 4 8 12 23 6 Σf = 60 Data yang paling sering muncul adalah pada interval 74 -86, sehingga : L 0 = 73, 5 b 1 = 23 -12 = 11 b 2 = 23 -6 =17

HUBUNGAN EMPIRIS ANTARA NILAI RATA-RATA HITUNG, MEDIAN, DAN MODUS Ada 3 kemungkinan kesimetrian kurva distribusi data : 1) Jika nilai ketiganya hampir sama maka kurva mendekati simetri. 2) Jika Mod<Med<rata-rata hitung, maka kurva miring ke kanan. 3) Jika rata-rata hitung<Med<Mod, maka kurva miring ke kiri.

KELEBIHAN & KEKURANGAN MEAN, MEDIAN, MODUS UKURAN PEMUSATAN v RATA-RATA HITUNG KELEBIHAN v v v MEDIAN v v v MODUS v v KEKURANGAN Mempertimbangkan semua nilai Dapat menggambarkan mean populasi Variasinya stabil Cocok untuk data homogen v Tidak peka atau tidak terpengaruh oleh nilai ekstrem Cocok untuk data heterogen v Tidak peka oleh nilai ektrem Cocok untuk data homogen maupun hiterogen v v Peka atau mudah terpengaruh oleh nilai ektrem Kurang baik untuk data heterogen Tidak mempertimbangkan semua nilai Kurang dapat menggambarkan mean populasi Kurang menggambarkan mean populasi Modus bisa lebih dari satu

HUBUNGAN EMPIRIS ANTARA NILAI RATA-RATA HITUNG, MEDIAN, DAN MODUS (lanjutan) Jika distribusi data tidak simetri, maka terdapat hubungan : Rata-rata hitung-Modus = 3 (Rata-rata hitung-Median)

4. RATA-RATA UKUR Digunakan apabila nilai data satu dengan yang lain berkelipatan. Untuk data tidak berkelompok Untuk data berkelompok

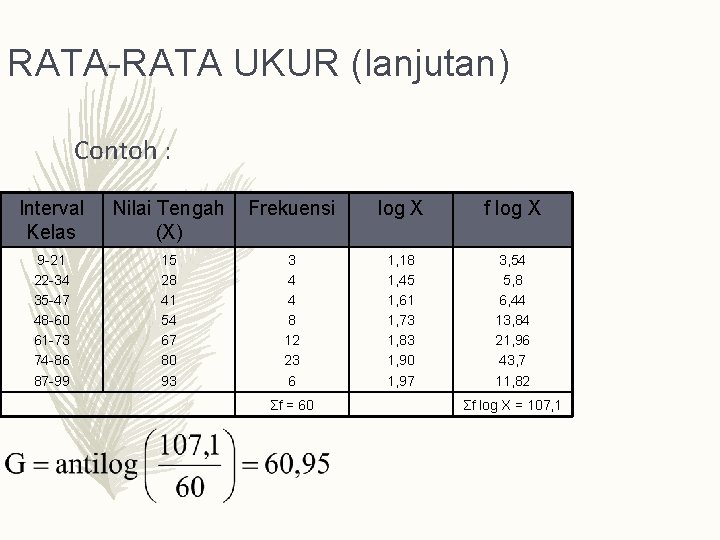
RATA-RATA UKUR (lanjutan) Contoh : Interval Kelas Nilai Tengah (X) Frekuensi log X f log X 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 15 28 41 54 67 80 93 3 4 4 8 12 23 6 1, 18 1, 45 1, 61 1, 73 1, 83 1, 90 1, 97 3, 54 5, 8 6, 44 13, 84 21, 96 43, 7 11, 82 Σf = 60 Σf log X = 107, 1

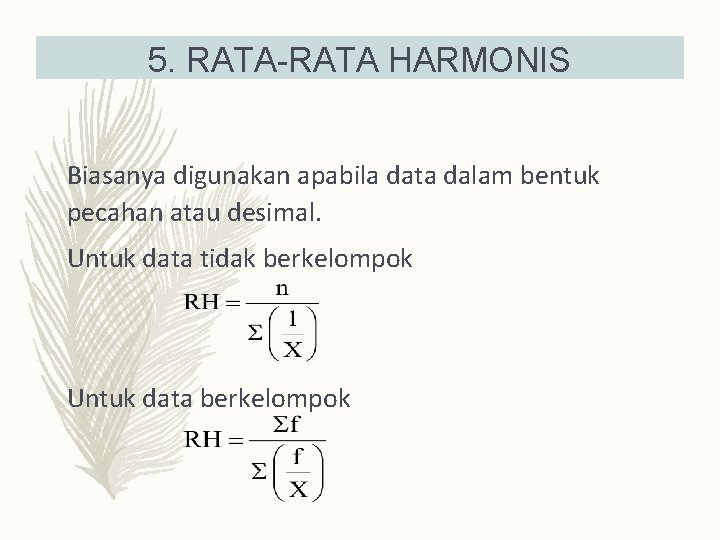
5. RATA-RATA HARMONIS Biasanya digunakan apabila data dalam bentuk pecahan atau desimal. Untuk data tidak berkelompok Untuk data berkelompok

5. RATA-RATA HARMONIS (lanjutan) Contoh : Interval Kelas Nilai Tengah (X) Frekuensi f/X 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 15 28 41 54 67 80 93 3 4 4 8 12 23 6 0, 2 0, 143 0, 098 0, 148 0, 179 0, 288 0, 065 Σf = 60 Σf / X = 1, 121

KUARTIL, DESIL, PERSENTIL 1. Kuartil Kelompok data yang sudah diurutkan (membesar atau mengecil) dibagi empat bagian yang sama besar. Ada 3 jenis yaitu kuartil pertama (Q 1) atau kuartil bawah, kuartil kedua (Q 2) atau kuartil tengah, dan kuartil ketiga (Q 3) atau kuartil atas.

KUARTIL (lanjutan) Untuk data tidak berkelompok Untuk data berkelompok L 0 = batas bawah kelas kuartil F = jumlah frekuensi semua kelas sebelum kelas kuartil Qi f = frekuensi kelas kuartil Qi

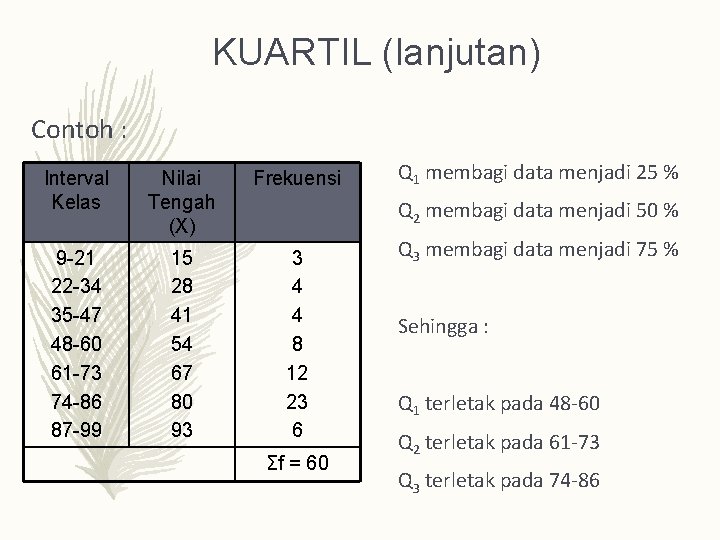
KUARTIL (lanjutan) Contoh : Interval Kelas Nilai Tengah (X) Frekuensi 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 15 28 41 54 67 80 93 3 4 4 8 12 23 6 Q 1 membagi data menjadi 25 % Q 2 membagi data menjadi 50 % Σf = 60 Q 3 membagi data menjadi 75 % Sehingga : Q 1 terletak pada 48 -60 Q 2 terletak pada 61 -73 Q 3 terletak pada 74 -86

KUARTIL (lanjutan) Untuk Q 1, maka : Untuk Q 2, maka : Untuk Q 3, maka :

50, 45, 60, 75, 80, 78, 90, 100 Langkah pertama yang dilakukan adalah mengurutkan data: 40, 45, 50, 60, 75, 78, 80, 90, 100

KUARTIL, DESIL, PERSENTIL (lanjutan) 2. Desil Kelompok data yang sudah diurutkan (membesar atau mengecil) dibagi sepuluh bagian yang sama besar.

DESIL (lanjutan) Untuk data tidak berkelompok Untuk data berkelompok L 0 = batas bawah kelas desil Di F = jumlah frekuensi semua kelas sebelum kelas desil Di f = frekuensi kelas desil Di

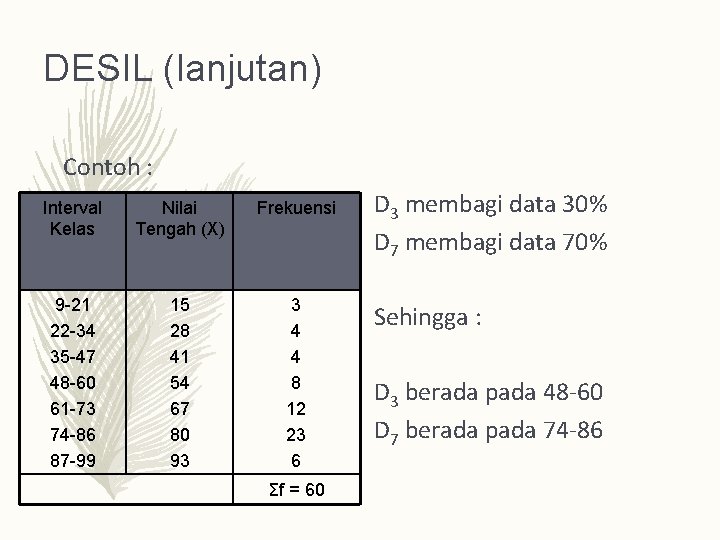
DESIL (lanjutan) Contoh : Interval Kelas Nilai Tengah (X) Frekuensi 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 15 28 41 54 67 80 93 3 4 4 8 12 23 6 Σf = 60 D 3 membagi data 30% D 7 membagi data 70% Sehingga : D 3 berada pada 48 -60 D 7 berada pada 74 -86

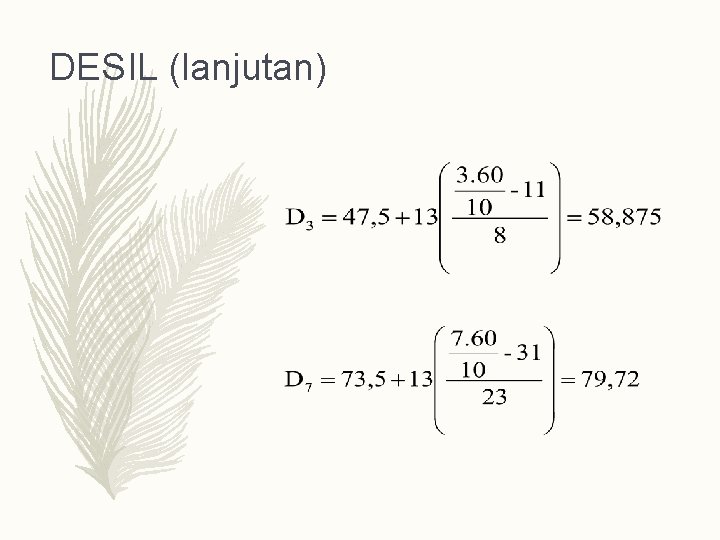
DESIL (lanjutan)

KUARTIL, DESIL, PERSENTIL (lanjutan) 3. Persentil Untuk data tidak berkelompok Untuk data berkelompok