Ukuran pemusatan data digunakan agar data yang diperoleh

Ukuran pemusatan data digunakan agar data yang diperoleh mudah untuk dibaca dan dipahami. Ukuran pemusatan data terdiri atas mean, median, dan modus.

1. Rata-rata / mean menjumlahkan seluruh angka data yang selanjutnya dibagi dengan banyaknya jumlah data

contoh Nilai ulangan matematika Anto pada semster 1 adalah 6, 8, 5, 7, 9, dan 7. Maka meannya adalah : 6 + 8 + 5 + 7 + 9 + 7 = 42 : 6 = 7

Mean data kelompok Misalkan sekumpulan data terdiri atas nilai X 1, X 2, X 3 … Xn dan memiliki frekuensi f 1, f 2, f 3, … fn maka mean dapat dicari dengan rumus : Contoh : Tentukan mean dari data berikut ! 6, 5, 6, 7, 8, 9, 5, 6, 8, 9, 9, 6, 7, 4, 5, 8, 7, 4, 8, 5

Jawab : Data diatas akan lebih mudah dikerjakan bila disajikan dalam tabel Tabel frekuensi :

Median • Contoh 1 Median adalah nilai tengah dari sekupulan data yang telah diurutkan dari terkecil ke terbesar. Median dipengaruhi oleh jumlah data, jika jumlah dta ganjil maka mediannya adalah nilai tengah dari data yang telah diurutkan, dan jika jumlah data genap maka mediannya adalah mean dari dua bilangan yang ditengah setelh data diurutkan. • Tentukan median dari data berikut! 3, 5, 4, 6, 8, 7, 3 Jawab : Jumlah data = 7 (ganjil) Data diurutkan akan menjadi seperti berikut: 3, 3, 4, 5, 6, 7, 8 Nilai 5 ada ditengah data yang telah diurutkan, maka 5 merupakan median. Contoh 2 : Tentukan median dari data berikut ! 9, 6, 5, 4, 3, 7, 8, 5 Jawab : Jumlah data = 8 (genap) Data diurutkan akan menjadi seperti berikut : 3, 4, 5, 5, 6, 7, 8, 9 nilai 5 dan 6 ada ditengah data yang telah diurutkan, maka mediannya adalah 5 + 6 / 2 = 5, 5

Median Data Kelompok Keterangan: Md = Median b = tepi bawah kelas median n = banyak data/jumlah sampel p = Panjang kelas interval F = Jumlah semua frekuensi sebelum kelas median f = Frekuensi Kelas Median

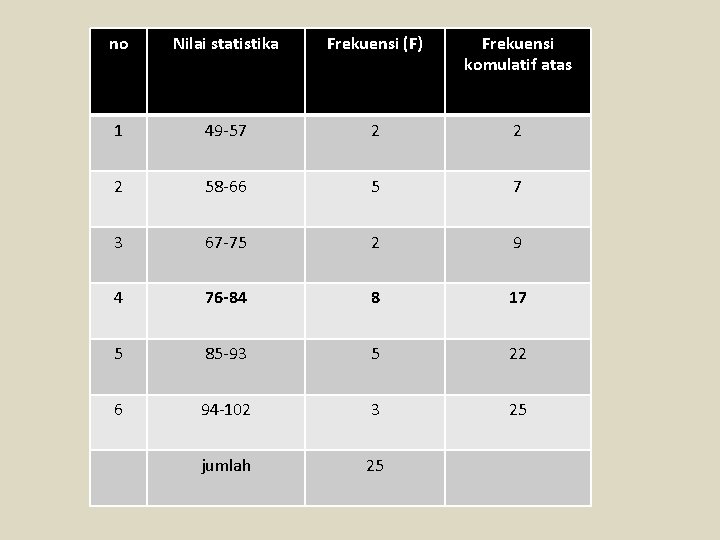
no Nilai statistika Frekuensi (F) Frekuensi komulatif atas 1 49 -57 2 2 2 58 -66 5 7 3 67 -75 2 9 4 76 -84 8 17 5 85 -93 5 22 6 94 -102 3 25 jumlah 25

Modus adalah nilai data yang paling sering muncul atau nilai data yang frekuensinya paling banyak, modus dinotasikan dengan Mo. Contoh : Tentukan modus dari data berikut ! 4, 8, 7, 4, 6, 3, 6, 8, 6, 3 Jawab : Data yang paling sering muncul adalah 6, maka Mo = 6

Keterangan Mo = Modus b = Batas kelas interval dengan frekuensi terbanyak p = Panjang kelas interval b 1 = Frekuensi pada kelas modus (frekuensi pada kelas interval yang terbanyak) dikurangi frekuensi kelas interval terdekat sebelumnya b 2 = Frekuensi pada kelas modus (frekuensi pada kelas interval yang terbanyak) dikurangi frekuensi kelas interval berikutnya contoh soal : Tentukan nilai modus data kelompok dari data berikut : 49, 54, 59, 59, 64, 66, 69, 74, 76, 78, 79, 79, 79, 84, 87, 89, 89, 92, 99

Kuartil adalah bilangan yang 'dapat dianggap‘ membagi data yang telah diurutkan menurut besarnya, dari yang terkecil ke yang terbesar, menjadi empat sub kelompok yang sama banyak. Ada 3 macam kuartil yakni: - Kuartil pertama (Q 1) - Kuartil kedua (Q 2) yang juga merupakan median, dan - Kuartil ketiga (Q 3) Nilai kuartil tidak harus terdapat pada data.

• Kuartil ke-i ialah bilangan yang 'dapat dianggap' sebagai data (skor) yang urutan besarnya bernomor i(n+1) : 4, i = 1, 2, 3 sehingga kuartil ke-i yang dilambangkan dengan Qi ditentukan oleh: Qi = i(n+1) : 4, dengan i = 1, 2, 3

contoh a. Berikut data berat badan (dalam satuan kilogram) dari 11 orang siswa: 49, 44, 62, 54, 38, 40, 53, 46, 45, 36, 42. Tentukan Q 1, Q 2, dan Q 3. b. Dari 11 siswa yang diukur tinggi badannya (dalam satuan sentimeter), diperoleh data sebagai berikut: 170, 162, 157, 158, 165, 173, 160, 159, 171, 168, 175, 180. Tentukan Q 1, Q 2, dan Q 3. c. Selama 12 hari dilakukan pengamatan terhadap jumlah pengunjung sebuah supermarket yang baru dibuka sehingga diperoleh data: 96, 70, 82, 50, 84, 71, 28, 64, 72, 68, 72, 50. Tentukan Q 1, Q 2, dan Q 3 ?

Jawab: a. Data diurutkan sehingga diperoleh: 36 38 40 42 44 45 46 49 53 54 62 (n = 11) Selanjutnya, Q 1, Q 2, dan Q 3 ditentukan sebagai berikut: Q 1 = skor ke 1(11+1) : 4 = skor ke 12 : 4 = skor ke 3 = 40. Jadi, Q 1 = 40 Q 2 = skor ke 2(11+1) : 4 = skor ke 24 : 4 = skor ke 6 = 45. Jadi, Q 2 = 45 Q 3 = skor ke 3(11+1) : 4 = skor ke 36 : 4 = skor ke 9 = 53. Jadi, Q 3 = 53

Desil ialah bilangan yang 'dapat dianggap‘ membagi data yang telah diurutkan menurut besarnya, dari yang terkecil ke yang terbesar, menjadi sepuluh sub kelompok yang sama banyak. Dengan demikian terdapat 9 macam desil yakni mulai dari desil pertama (D 1) sampai dengan desil kesembilan (D 9).

Desil ke-i ialah bilangan yang 'dapat dianggap' sebagai data (skor) yang urutan besarnya bernomor i(n+1) : 10 , i = 1 , 2 , 3 , … , 9 sehingga desil ke-i yang dilambangkan dengan (Di) Di ditentukan oleh: Di = skor ke i(n+1) : 10 , dengan I = 1, 2, 3, 4, 5, 6, 7, 8, 9 Sebagaimana kuartil, nilai desil juga tidak harus terdapat pada data.

contoh • Tentukan nilai D 6 dari data pengamatan terhadap jumlah pengunjung sebuah toko buku yang baru dibuka sebagai berikut: 9, 9, 10, 13, 14, 17, 19, 21, 22, 23, 25, 27, 29, 33, 35, 39, 43, 47. Jawab: Data sudah diurutkan yakni: 9, 9, 10, 13, 14, 17, 19, 21, 22, 23, 25, 27, 29, 33, 35, 39, 43, 47. ( n= 20)

Selanjutnya D 6 ditentukan sebagai berikut: D 6 = skor ke 6(20+1) : 10 = 126 : 10 = skor ke 12, 6 D 6 = skor ke 12 + 0, 6 ( skor ke-13 – skor ke-12) = 25 + 0, 6 ( 27 – 25) = 25 + 1, 2 = 26, 2

Presentil Persentil ialah bilangan yang 'dapat dianggap‘ membagi data yang telah diurutkan menurut besarnya, dari yang terkecil ke yang terbesar, menjadi 100 sub kelompok yang sama banyak. Dengan demikian terdapat 99 macam persentil yakni mulai dari persentil pertama (P 1) sampai dengan persentil ke sembilan puluh sembilan (P 99). Mudah dipahami bahwa Median = Q 2 = D 5 = P 50

• Serupa dengan cara menghitung kuartil dan desil di atas, persentil ke-i ialah bilangan yang 'dapat dianggap' sebagai data (skor) yang urutan besarnya bernomor i(n+1) : 100, dengan i = 1, 2, 3, … , 99 sehingga persentil ke-i yang dilambangkan dengan Pi ditentukan oleh: Pi = skor i(n+1) : 100, dengan i = 1, 2, 3, … , 99 Sebagaimana kuartil dan desil, nilai persentil juga tidak harus terdapat pada data.

Selesai