Valid and Invalid Arguments Lecture 3 Section 1

Valid and Invalid Arguments Lecture 3 Section 1. 3 Mon, Jan 23, 2006

Arguments An argument is a sequence of statements. ¢ The last statement is the conclusion. ¢ All the other statements are the premises. ¢ A mathematical proof is an argument. ¢

Argument Forms An argument form is a sequence of statement forms. ¢ The last statement form is the conclusion. ¢ All the other statement forms are the premises. ¢ A mathematical proof follows an argument form. ¢

Validity of an Argument Form An argument form is valid if its conclusion is true when its premises are true. ¢ Otherwise, the argument form is invalid. ¢ An invalid argument form is called a fallacy. ¢

Validity of an Argument ¢ An argument is valid if its argument form is valid, whether or not its premises are true.

The Form of an Argument Let the premises be P 1, …, Pn. ¢ Let the conclusion be C. ¢ The argument form is valid if P 1 Pn C is a tautology. ¢

Example I will ride my bike today. ¢ If it is raining and I ride my bike, then I will get wet. ¢ It is raining. ¢ Therefore, I will get wet. ¢

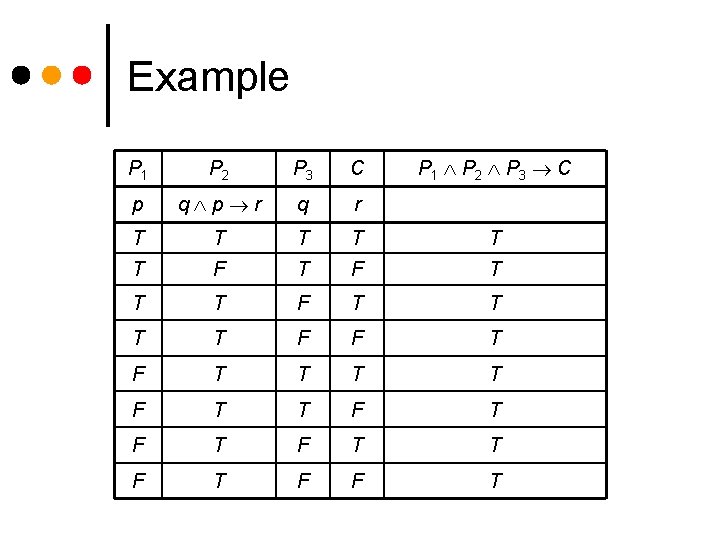
Example ¢ ¢ p = “I will ride my bike today. ” q = “It is raining. ” r = “I will get wet. ” Argument form: p q p r q r

Example P 1 P 2 P 3 C P 1 P 2 P 3 C p q p r q r T T T F T T F F T T T T F T F T T F F T

Example: Invalid Argument Forms with True Conclusions ¢ An argument form may be invalid even though its conclusion is true. If I eat my vegetables, I’ll be big and strong. l I’m big and strong. l Therefore, I ate my vegetables. l ¢ A true conclusion does not ensure that the argument form is valid.

Example: Valid Argument Forms with False Conclusions ¢ An argument form may be valid even though its conclusion is false. If I wait until the last minute to do my homework, then it will be a lot easier. l I wait until the last minute to do my homework. l Therefore, it will be a lot easier. l ¢ A false conclusion does not mean that the argument form is invalid.

Example: Valid Argument Forms with False Conclusions ¢ Another example. If 1 + 1 = 2, then pigs can fly. l 1 + 1 = 2. l Therefore, pigs can fly. l

Modus Ponens Modus ponens is the argument form p q ¢ This is also called a direct argument. ¢

Examples of Modus Ponens If it is raining, then I am carrying my umbrella. It is raining. Therefore, I am carrying my umbrella. ¢ If pigs can fly, then I am carrying my umbrella. Pigs can fly. Therefore, I am carrying my umbrella. ¢

Modus Tollens Modus tollens is the argument form p q q p ¢ This is also called an indirect argument. ¢ It is equivalent to replacing p q with q p and then using modus ponens. ¢

Examples of Modus Tollens If it is raining, then I am carrying my umbrella. I am not carrying my umbrella. Therefore, it is not raining. ¢ If pigs can fly, then I am carrying my umbrella. I am not carrying my umbrella. Therefore, pigs cannot fly. ¢

Other Argument Forms From the specific to the general p p q ¢ From the general to the specific p q p ¢

Other Argument Forms Elimination p q ¢ Transitivity p q q r p r ¢

Other Argument Forms ¢ Division into Cases p q p r q r r

Fallacies A fallacy is an invalid argument form. ¢ Two common fallacies ¢ The fallacy of the converse. l The fallacy of the inverse. l

The Fallacy of the Converse The fallacy of the converse is the invalid argument form p q q p ¢ This is also called the fallacy of affirming the consequent. ¢

Example ¢ If it is raining, then I am carrying an umbrella. Therefore, it is raining.

Fallacy of the Inverse The fallacy of the inverse is the invalid argument form p q p q ¢ This is also called the fallacy of denying the antecedent. ¢

Example ¢ If pigs can fly, then I am carrying an umbrella. Pigs cannot fly. Therefore, I am not carrying an umbrella.