Graphical Visualization A Particular Theory A proof The























- Slides: 38






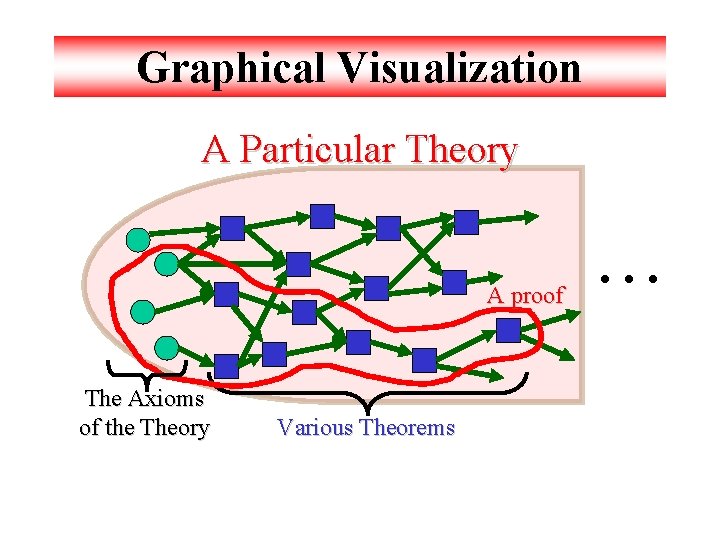
Graphical Visualization A Particular Theory A proof The Axioms of the Theory Various Theorems …




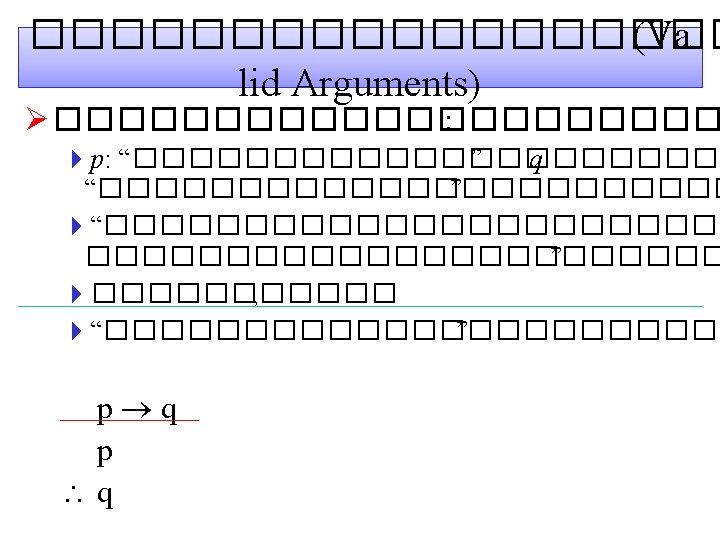
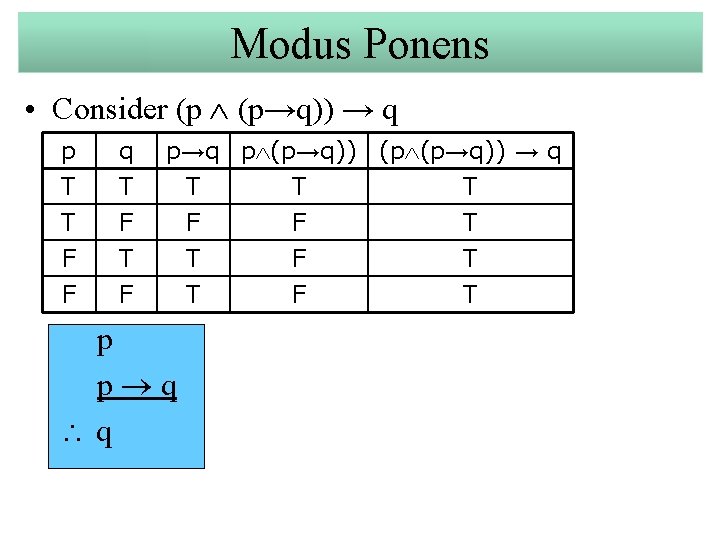
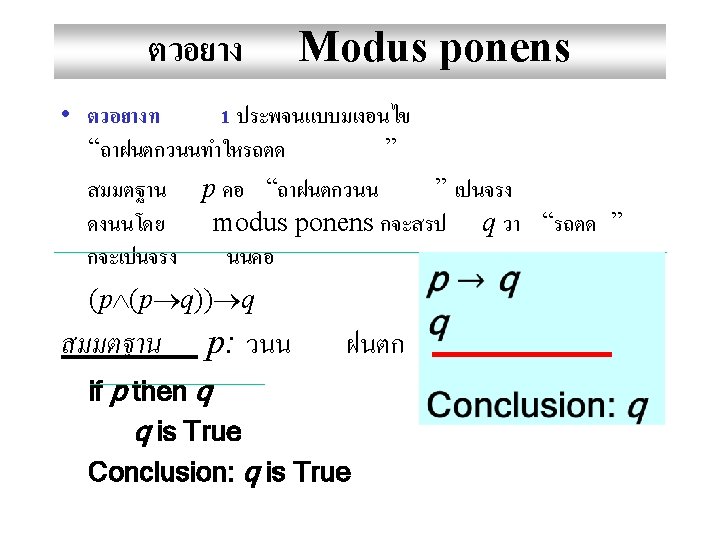
Modus Ponens • Consider (p (p→q)) → q p T T F q T F F p→q p (p→q)) (p (p→q)) → q T T T F F T T F T p p q q T F T


Modus Tollens • Assume that we know: ¬q and p → q – Recall that p → q ¬q → ¬p • Thus, we know ¬q and ¬q → ¬p • We can conclude ¬p q p


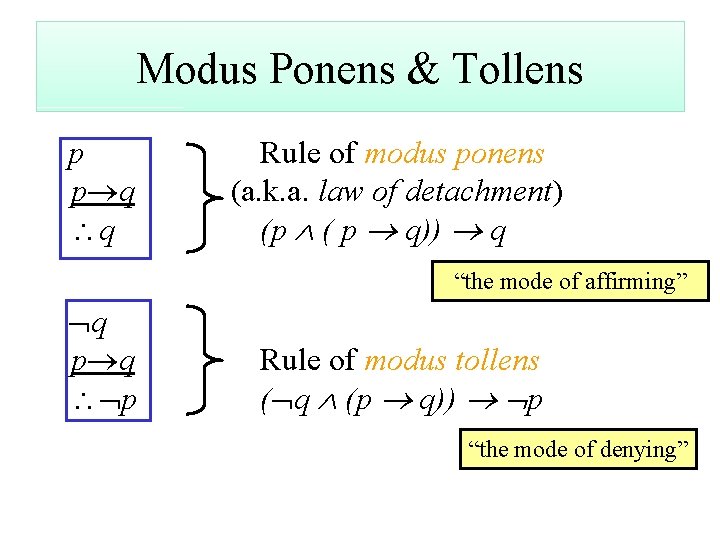
Modus Ponens & Tollens p p q q Rule of modus ponens (a. k. a. law of detachment) (p ( p q)) q “the mode of affirming” q p q p Rule of modus tollens ( q (p q)) p “the mode of denying”




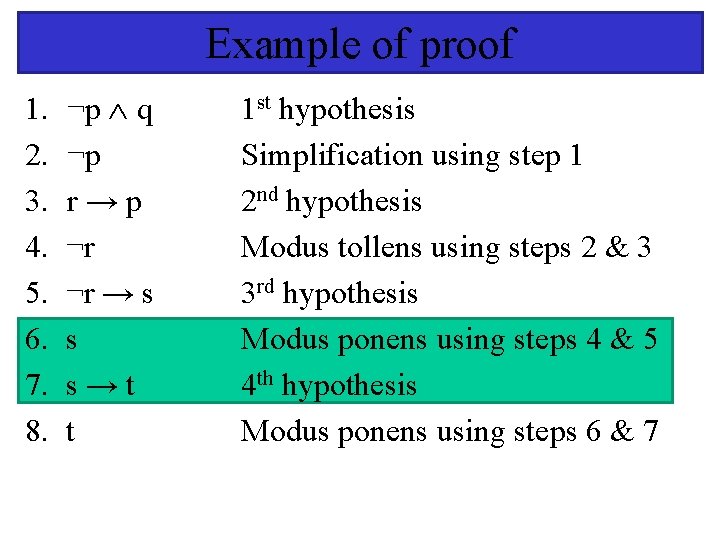
Example of proof 1. ¬p q 2. ¬p 1 st hypothesis Simplification using step 1

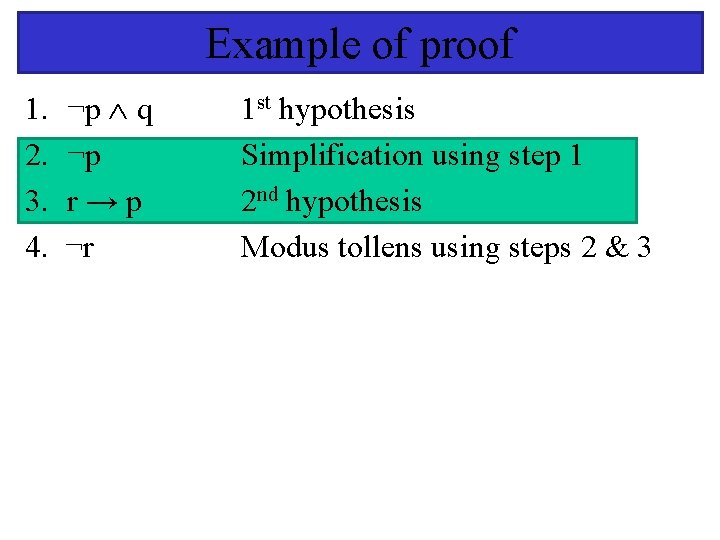
Example of proof 1. ¬p q 2. ¬p 3. r → p 4. ¬r 1 st hypothesis Simplification using step 1 2 nd hypothesis Modus tollens using steps 2 & 3

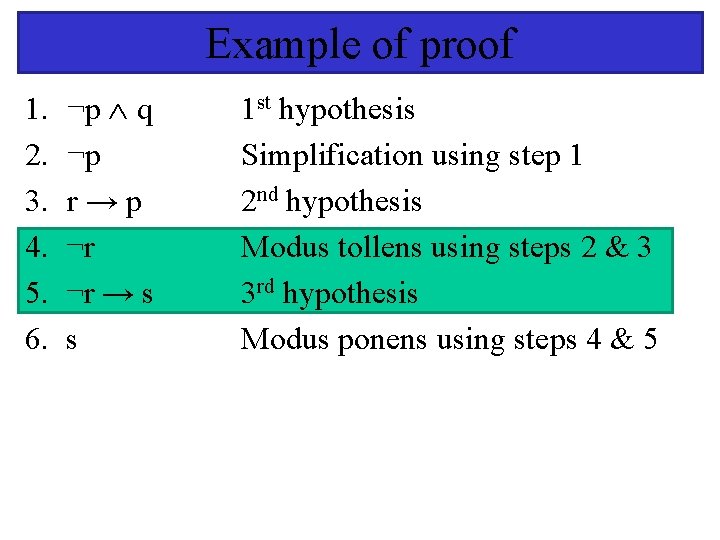
Example of proof 1. 2. 3. 4. 5. 6. ¬p q ¬p r → p ¬r ¬r → s s 1 st hypothesis Simplification using step 1 2 nd hypothesis Modus tollens using steps 2 & 3 3 rd hypothesis Modus ponens using steps 4 & 5

Example of proof 1. 2. 3. 4. 5. 6. 7. 8. ¬p q ¬p r → p ¬r ¬r → s s s → t t 1 st hypothesis Simplification using step 1 2 nd hypothesis Modus tollens using steps 2 & 3 3 rd hypothesis Modus ponens using steps 4 & 5 4 th hypothesis Modus ponens using steps 6 & 7

More Rules of Inference • Conjunction: if p and q are true separately, then p q is true • Resolution: If p q is true, and ¬p r is true, then q r must be true

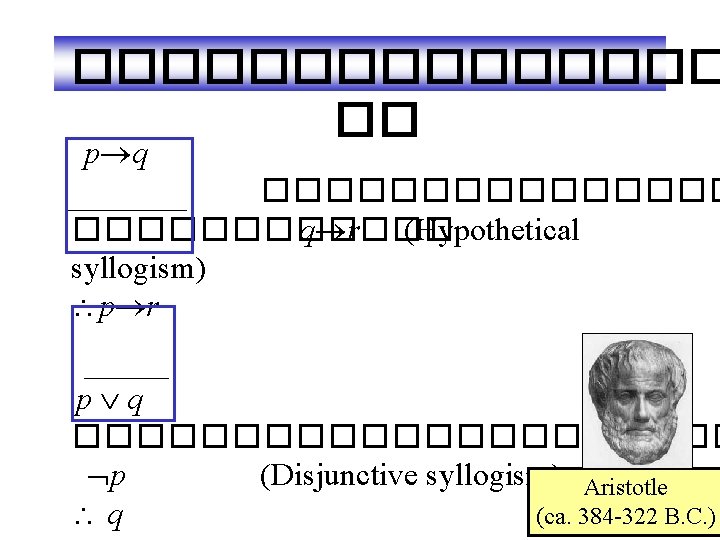
�������� �� p q �������� q r (Hypothetical syllogism) p r p q ����������� p (Disjunctive syllogism) Aristotle (ca. 384 -322 B. C. ) q

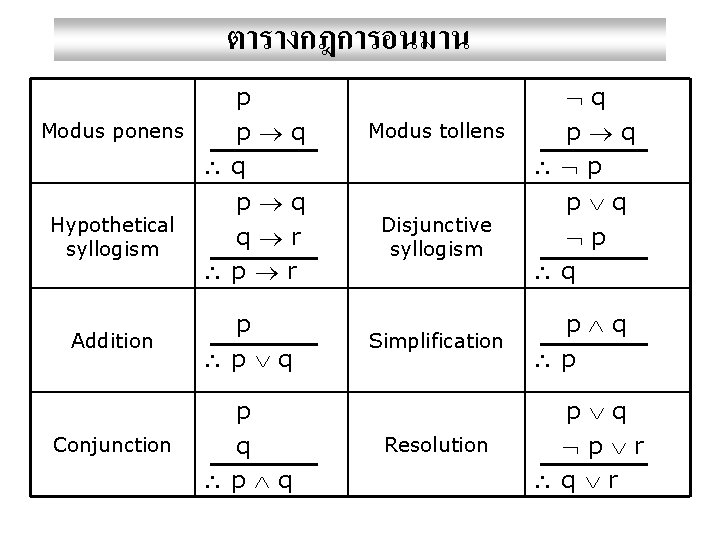
ตารางกฎการอนมาน p Modus ponens p q q Hypothetical syllogism p q q r p r Addition p p q Conjunction p q Modus tollens q p q p Disjunctive syllogism p q Simplification p q p Resolution p q p r q r

Resolution p q r T T T F F F F T T T T F F F T F F


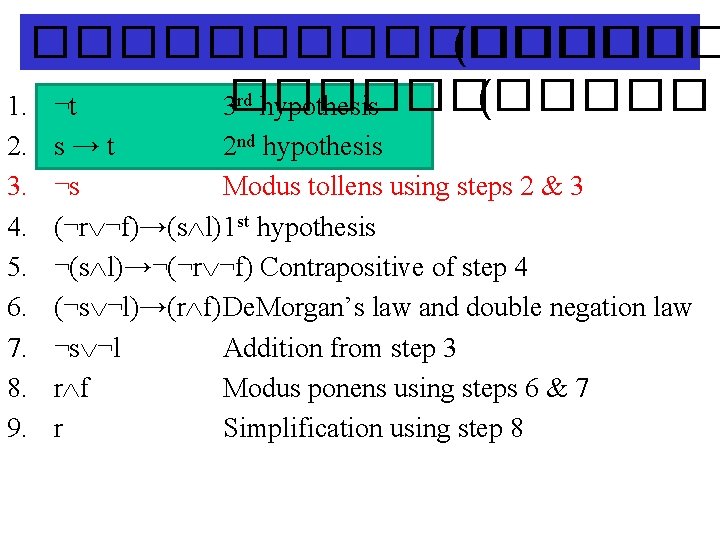
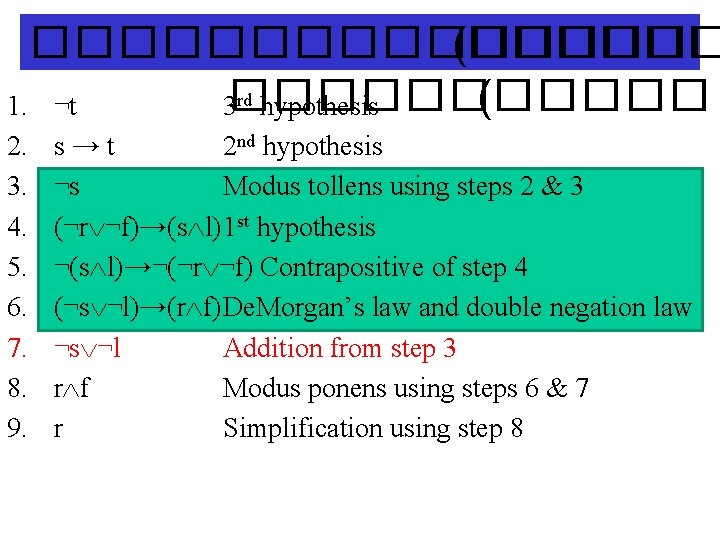
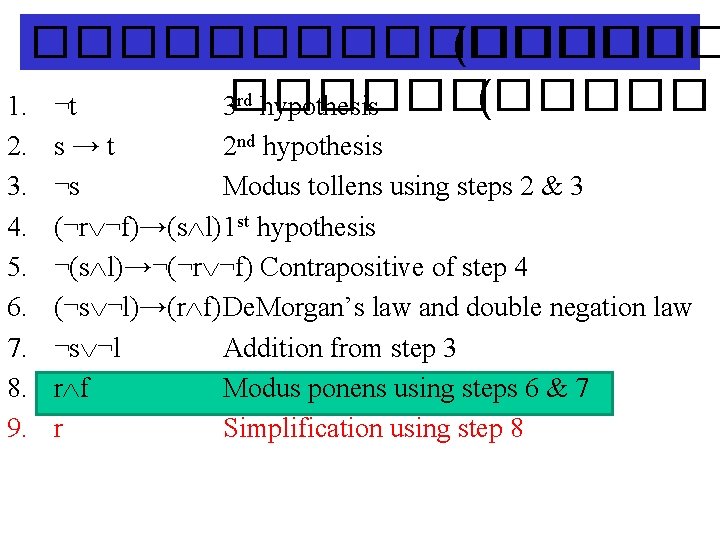
�������� (������ rd hypothesis ( 1. ¬t 3������ 2. 3. 4. 5. 6. 7. 8. 9. s → t 2 nd hypothesis ¬s Modus tollens using steps 2 & 3 (¬r ¬f)→(s l)1 st hypothesis ¬(s l)→¬(¬r ¬f) Contrapositive of step 4 (¬s ¬l)→(r f)De. Morgan’s law and double negation law ¬s ¬l Addition from step 3 r f Modus ponens using steps 6 & 7 r Simplification using step 8

�������� (������ rd hypothesis ( 1. ¬t 3������ 2. 3. 4. 5. 6. 7. 8. 9. s → t 2 nd hypothesis ¬s Modus tollens using steps 2 & 3 (¬r ¬f)→(s l)1 st hypothesis ¬(s l)→¬(¬r ¬f) Contrapositive of step 4 (¬s ¬l)→(r f)De. Morgan’s law and double negation law ¬s ¬l Addition from step 3 r f Modus ponens using steps 6 & 7 r Simplification using step 8

�������� (������ rd hypothesis ( 1. ¬t 3������ 2. 3. 4. 5. 6. 7. 8. 9. s → t 2 nd hypothesis ¬s Modus tollens using steps 2 & 3 (¬r ¬f)→(s l)1 st hypothesis ¬(s l)→¬(¬r ¬f) Contrapositive of step 4 (¬s ¬l)→(r f)De. Morgan’s law and double negation law ¬s ¬l Addition from step 3 r f Modus ponens using steps 6 & 7 r Simplification using step 8

�������� (������ rd hypothesis ( 1. ¬t 3������ 2. 3. 4. 5. 6. 7. 8. 9. s → t 2 nd hypothesis ¬s Modus tollens using steps 2 & 3 (¬r ¬f)→(s l)1 st hypothesis ¬(s l)→¬(¬r ¬f) Contrapositive of step 4 (¬s ¬l)→(r f)De. Morgan’s law and double negation law ¬s ¬l Addition from step 3 r f Modus ponens using steps 6 & 7 r Simplification using step 8




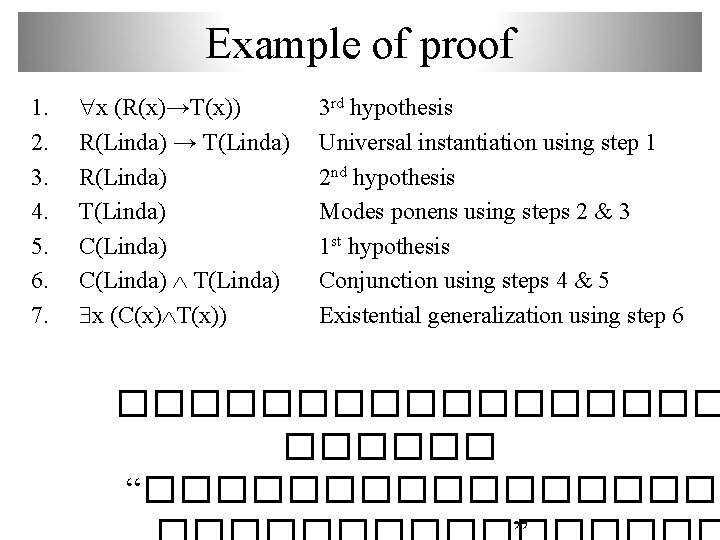
Example of proof 1. 2. 3. 4. 5. 6. 7. x (R(x)→T(x)) R(Linda) → T(Linda) R(Linda) T(Linda) C(Linda) T(Linda) x (C(x) T(x)) 3 rd hypothesis Universal instantiation using step 1 2 nd hypothesis Modes ponens using steps 2 & 3 1 st hypothesis Conjunction using steps 4 & 5 Existential generalization using step 6 ��������� “���������

Example of proof • Given the hypotheses: – “There is someone in this class who x (C(x) F(x)) has been to France” x (F(x)→L(x)) – “Everyone who goes to France visits the Louvre” • Can you conclude: “Someone in this class has visited the Louvre”? x (C(x) L(x))

Example of proof 1. 2. 3. 4. 5. 6. 7. 8. 9. x (C(x) F(x)) C(y) F(y) C(y) x (F(x)→L(x)) F(y) → L(y) C(y) L(y) x (C(x) L(x)) 1 st hypothesis Existential instantiation using step 1 Simplification using step 2 2 nd hypothesis Universal instantiation using step 5 Modus ponens using steps 3 & 6 Conjunction using steps 4 & 7 Existential generalization using step 8 Thus, we have shown that “Someone in this class has visited the Louvre”

How do you know which one to use? • Experience! • In general, use quantifiers with statements like “for all” or “there exists”