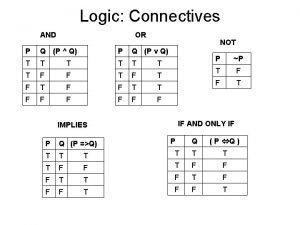
Ch 1 5 Basic Proof Methods II Proof

Ch 1. 5: Basic Proof Methods II Proof by Contraposition of P => Q Suppose ~Q …proof details here…. Therefore, ~P (via a direct proof) Thus, ~Q => ~P. Therefore, P => Q

Example 1 Let m be an integer. Prove that if m^2 is even, then m is even. Proof: Suppose that m is odd. Then m = 2 k +1 for some integer k. It follows that m^2 = (2 k+1)^2 = 4 k^2 + 4 k + 1 m^2 = 2(2 k^2 + 2 k) + 1 m^2 = 2 n+1, where n = 2 n+1 is an integer. Thus m^2 is odd. Therefore, m odd implies m^2 is odd. Hence m^2 even implies m even, by contraposition.

Example 2 Prove Let x be a positive real number. Prove that if x > 1, then x^2 – 1 > 0. Proof: Suppose x is positive and x^2 -1 <= 0. Then (x-1)(x+1) <= 0. It follows that 0 < x <= 1. Therefore, x^2 -1 <= 0 implies x <= 1. Hence for x positive, x > 1 implies x^2 – 1 > 0, by contraposition.

Contradiction Proof by Contradiction. Want to prove P. Suppose ~P …proof details here…. Therefore, Q. …proof details here…. Therefore, ~Q. Thus, Q/ ~Q, a contradiction. Therefore, P. Note: Q is not necessarily known at onset of proof.

Example 3 Prove that sqrt(2) is irrational. Proof: Assume false: sqrt(2) = p/q for integers p, q. WLOG, assume p & q have no common factors. Then 2 = p^2/q^2 => 2 q^2 = p^2. Thus p^2 is even, and hence p is even (by Example 1). Since p & q have no common factors, q is odd. Now p is even, so p = 2 k for some integer k. Thus p^2 = 4 k^2, hence 2 q^2 = 4 k^2 (since 2 q^2 = p^2). Then q^2 = 2 k^2, and therefore q is even (by Example 1). This is a contradiction. Hence sqrt(2) is irrational.

Example 4 Prove that the set of primes is infinite. Proof: Assume false: Let {p 1, p 2, …pk} be the set of primes, k in N. Let n = (p 1*p 2*…*pk) + 1. Since n is in N, it has a prime divisor q > 1. (See Ch 2. 5. ) Thus q divides n. Now q is in {p 1, p 2, …pk}, so it divides p 1*p 2*…*pk. Therefore, q divides n - p 1*p 2*…*pk. (See Ch 1. 4, p 32. ) But n - p 1*p 2*…*pk = 1. Thus q divides 1, which implies q = 1. This is a contradiction. Hence the set of primes is infinite.

Biconditional Two-Part Proof of a Biconditional P Q. Show P => Q by any method Also, show Q => P by any method. Therefore, P Q.

Example 5 Let a be a prime; b, c in N. Prove that a|bc iff a|b or a|c. Proof: Let a be a prime and b, c in N. (=>) Suppose a|bc. Then bc = ka, for some k in N. Also, b = p 1 p 2…pm, c = q 1 q 2…qn, pi and qi prime. Then bc = (p 1 p 2…pm)(q 1 q 2…qn) Since a is prime and a|bc, a = pi for some i or a = qj for some j. Thus either b is an integer multiple of a or c is an integer multiple of a. Therefore a|b or a|c.

Example 5 Let a be a prime; b, c in N. Prove that a|bc iff a|b or a|c. Proof: Let a be a prime and b, c in N. (<=) Suppose a|b or a|c. Then b = ma for some m in N or c = na, for some n in N. Thus bc = (ma)c = (mc)a = ka, k = mc in N or bc = b(na) = (bn)a = ja, j = bn in N Therefore a|b or a|c.

Example 6 Sometimes it is possible to prove both case of a biconditional simultaneously.

Basic Proof Methods Summary In this section and the last one we learned how to prove P => Q using a direct proof and a proof by contraposition. We learned how to prove P using contradiction. We learned how to prove P Q by proving the cases P => Q and Q => P separately or simultaneously. Sometimes we can prove a proposition by more than one method. See example on page 41. Most propositions can be proved true or false. Some cannot, and they are called undecidables. (This doesn’t happen in Math 240!).

Homework Read Ch 1. 5 Do 43(3 a-d, 4 a, b, 6 a-c, 7 a, b, 12 a-d)
- Slides: 12