STATISTIK 1 Pertemuan 5 Ukuran Pemusatan dan Penyebaran

STATISTIK 1 Pertemuan 5: Ukuran Pemusatan dan Penyebaran Data Kelompok Dosen Pengampu MK: Evellin Lusiana, S. Si, M. Si

Mean Data Berkelompok Jika nilai n buah data adalah x 1, x 2, x 3, … xn, dan masing frekuensi adalah f 1, f 2, f 3, … fn, maka mean data tersebut didefinisikan sebagai berikut. = jumlah hasil perkalian setiap data dan frekuensinya fi = frekuensi data ke-I xi = data ke-i (atau xi= ½. (batas bawah + batas) fi = N = jumlah data

Median Data Berkelompok Med = median Lo = tepi bawah kelas median c = panjang kelas interval kelas median n = banyaknya data pengamatan F = jumlah frekuensi sebelum kelas median f = frekuensi kelas median Kelas median = ½ n

Modus Data Berkelompok Mod = Lo = c = n = b 1 = modus tepi bawah kelas modus panjang kelas interval kelas modus banyaknya data pengamatan selisih antara frekuensi kelas modus dengan frekuensi kelas sebelum kelas modus b 2 = selisih antara frekuensi kelas modus dengan frekuensi kelas setelah kelas modus Kelas modus = kelas dengan frekuensi tertinggi

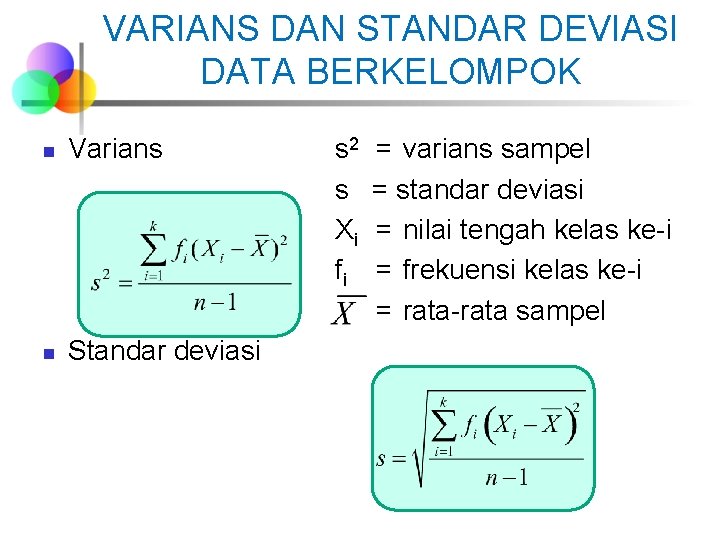
VARIANS DAN STANDAR DEVIASI DATA BERKELOMPOK n Varians n Standar deviasi s 2 s Xi fi = varians sampel = standar deviasi = nilai tengah kelas ke-i = frekuensi kelas ke-i = rata-rata sampel

Contoh: Berikut ini adalah data jumlah nasabah yg dilayani oleh CS di salah satu cabang Bank A selama 20 hari. 24, 35, 17, 21, 24 , 37, 26, 46, 58, 30, 32, 13, 12, 38, 41, 43, 44, 27, 53, 27

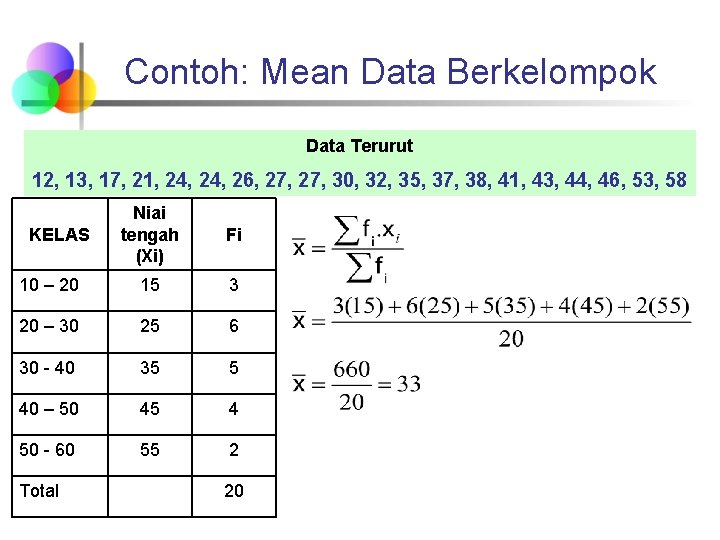
Contoh: Mean Data Berkelompok Data Terurut 12, 13, 17, 21, 24, 26, 27, 30, 32, 35, 37, 38, 41, 43, 44, 46, 53, 58 Niai tengah (Xi) Fi 10 – 20 15 3 20 – 30 25 6 30 - 40 35 5 40 – 50 45 4 50 - 60 55 2 KELAS Total 20

Contoh: Median Data Berkelompok n Niai tengah (Xi) Fi 10 – 20 15 3 20 – 30 25 6 KELAS n n n 30 - 40 35 5 40 – 50 45 4 50 - 60 55 2 Total 20 n Letak median = ½ 20 = 10 Kelas median = 30 -40 c = 40 – 30 = 10 n = 20 F = 3+6 =9 f = 5 Lo = 30 – 0, 5 = 29, 5

Contoh: Modus Data Berkelompok Niai tengah (Xi) Fi 10 – 20 15 3 20 – 30 25 6 30 - 40 35 5 40 – 50 45 4 50 - 60 55 2 KELAS Total 20 Kelas modus = 20 -30 Lo = 20 -0. 5=19. 5 c = 30 -20 =10 n = 20 b 1 = 6 -3 = 3 b 2 = 6 -5 = 1 Banyaknya nasabah yg paling sering dilayani oleh CS adalah sebanyak 27 org/hari

Contoh: Varians Data Berkelompok KELAS Niai tengah (Xi) 10 – 20 15 15 -33=-18 (-18)2=324 3 3(324)= 972 20 – 30 25 25 -33=-8 (-8)2=64 6 6(64)=384 30 - 40 35 35 -33=2 22=4 5 5(4)=20 40 – 50 45 45 -33=12 122=144 4 4(144)=576 50 - 60 55 55 -33=22 222=484 2 2(484)=968 20 2920 Total Fi Selisih jlh nasabah yg dilayani CS antar hari adalah 12 org/hr

Latihan n n Jumlah penduduk berumur 20 tahun ke atas yang bekerja menurut jam kerja selama seminggu. Jam Kerja 0 – 10 10 – 20 20 – 30 Frekuensi 3 7 10 30 – 40 5 Hitung mean, median, modus, varians

TUGAS 1. Sebuah firma audit akuntansi Rowatti dan Kopell khusus menangani pajak penghasilan dari para profesional seperti dokter, arsitek, pengacara, dsb. Firma tersebut mempekerjakan 20 akuntan. Tahun lalu, jumlah pajak yang ditangani setiap akuntan adalah sebagai berikut 53 ** 55 41 15 34 ** ** 45 51 64 20 23 34 ** 18 21 26 24 26 ** : diisi 2 angka nim terakhir n Buat tabel distribusi frekuensi dari data tsb n Dari tabel frekuensi yg ada, hitunglah n n mean, median, dan modus. Interpretasi! Varians dan standar deviasi. Interpretasikan nilai standar deviasi yg diperoleh