An Introduction to Statistics Two Branches of Statistical

An Introduction to Statistics

Two Branches of Statistical Methods n Descriptive statistics n Techniques for describing data in abbreviated, symbolic fashion n Inferential statistics n Drawing inferences based on data. Using statistics to draw conclusions about the population from which the sample was taken.

Populations and Samples n A parameter is a characteristic of a population n e. g. , the average height of all Americans. n A statistics is a characteristic of a sample n e. g. , the average height of a sample of Americans. n Inferential statistics infer population parameters from sample statistics n e. g. , we use the average height of the sample to estimate the average height of the population

Descriptive Statistics Numerical Data Properties Shape Central Tendency Variation Skewness Mean Range Kurtosis Median Interquartile Range Standard Deviation Mode Variance

Ordering the Data: Frequency Tables n Frequency table (distribution) n A listing in order of magnitude of each score achieved and the number of times the score occurred. n Grouped frequency table (distribution) n Range of scores in each of several equally sized intervals n Why Frequency Tables? n Gives some order to a set of data n Can examine data for outliers n Is an introduction to distributions

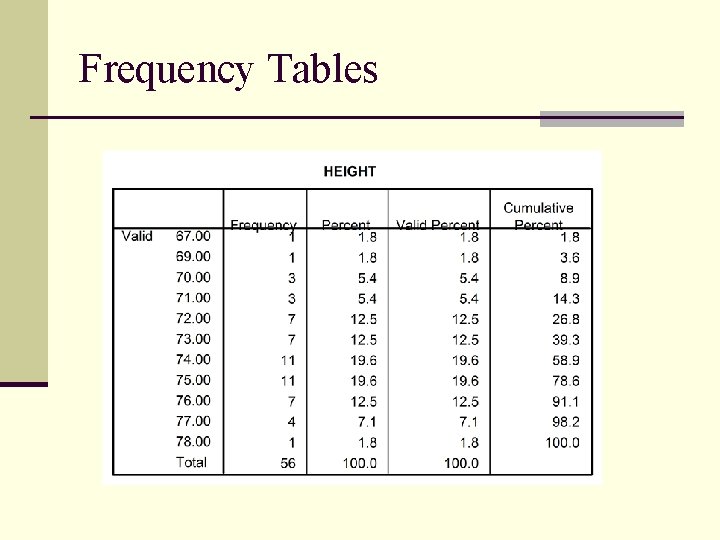
Frequency Tables

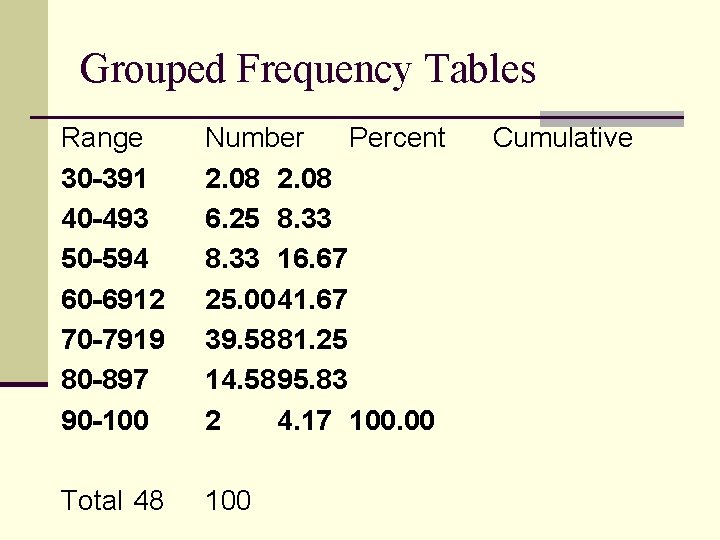
Grouped Frequency Tables Range 30 -391 40 -493 50 -594 60 -6912 70 -7919 80 -897 90 -100 Number Percent 2. 08 6. 25 8. 33 16. 67 25. 0041. 67 39. 5881. 25 14. 5895. 83 2 4. 17 100. 00 Total 48 100 Cumulative

Making a Frequency Table List each possible value, from highest to lowest 2) Go one by one through the scores, making a mark for each score next to its value on the list 3) Make a table showing how many times each value on your list was used 4) Calculate the percentage of scores for each value 1)

Making a Stem-and-Leaf Plot n Each data point is broken down into a “stem” and a “leaf. ” Select one or more leading digits for the stem values. The trailing digit(s) becomes the leaves n First, “stems” are aligned in a column. n Record the leaf for every observation beside the corresponding stem value

Stem and Leaf Plot n n n n n Stem-and-leaf of Shoes 12 63 (33) 43 25 12 8 4 4 2 2 1 1 1 N = 139 Leaf Unit = 1. 0 0 223334444444 0 5555555666667777777888888899999 1 00000001111222223333444 1 55556667777888 2 00000023 2 5557 3 0023 3 4 00 4 50 5 6 6 7 75

Stem and Leaf / Histogram Stem Leaf 2 3 4 5 1 2 3 4 2 3 6 8 8 5 By rotating the stem-leaf, we can see the shape of the distribution of scores. 6 Leaf Stem 4 3 8 3 2 8 5 1 2 3 2 2 3 4 5

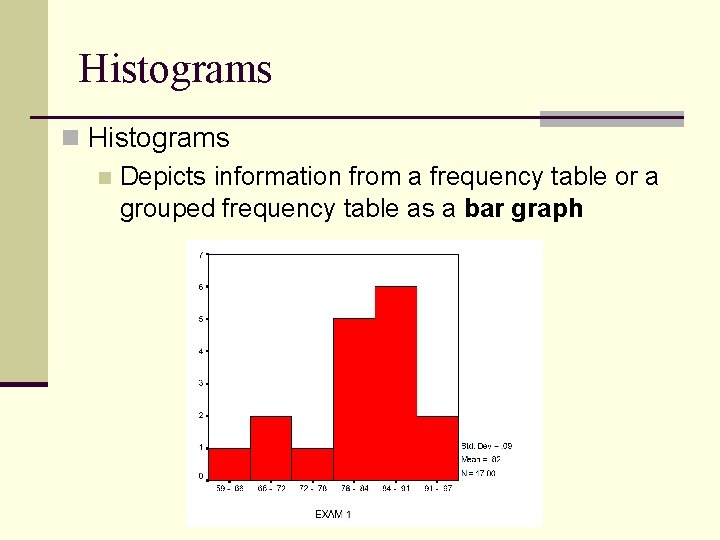
Histograms n Depicts information from a frequency table or a grouped frequency table as a bar graph

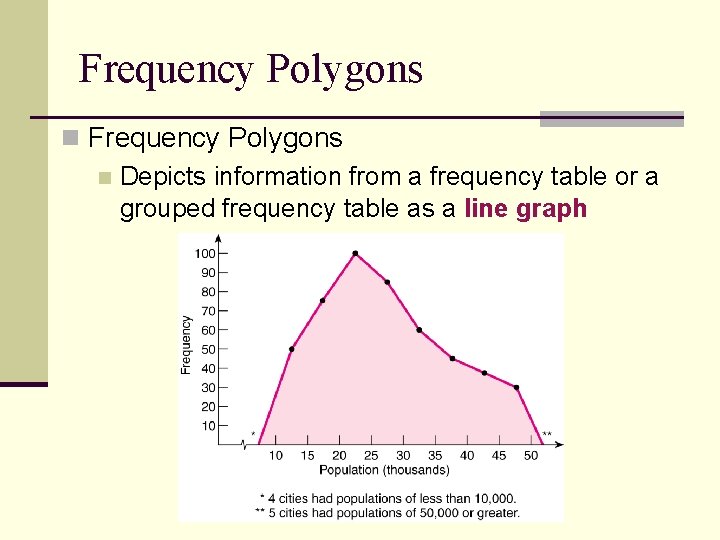
Frequency Polygons n Depicts information from a frequency table or a grouped frequency table as a line graph

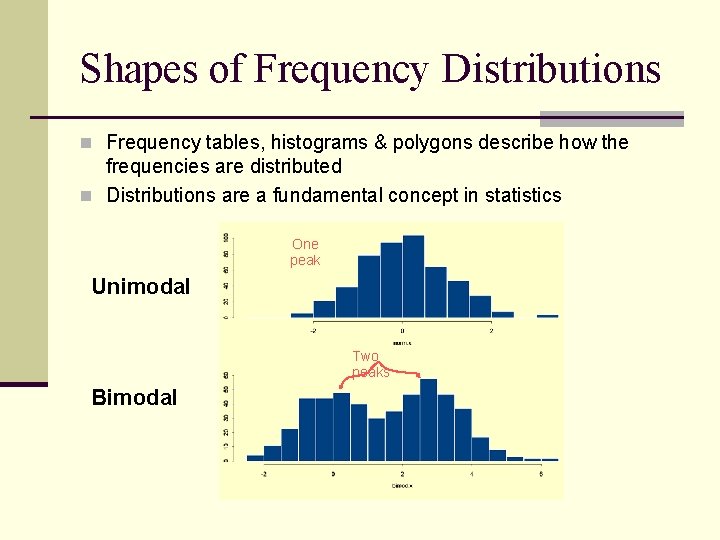
Shapes of Frequency Distributions n Frequency tables, histograms & polygons describe how the frequencies are distributed n Distributions are a fundamental concept in statistics One peak Unimodal Two peaks Bimodal

Symmetrical vs. Skewed Frequency Distributions n Symmetrical distribution n Approximately equal numbers of observations above and below the middle n Skewed distribution n One side is more spread out that the other, like a tail n Direction of the skew n n n Positive or negative (right or left) Side with the fewer scores Side that looks like a tail

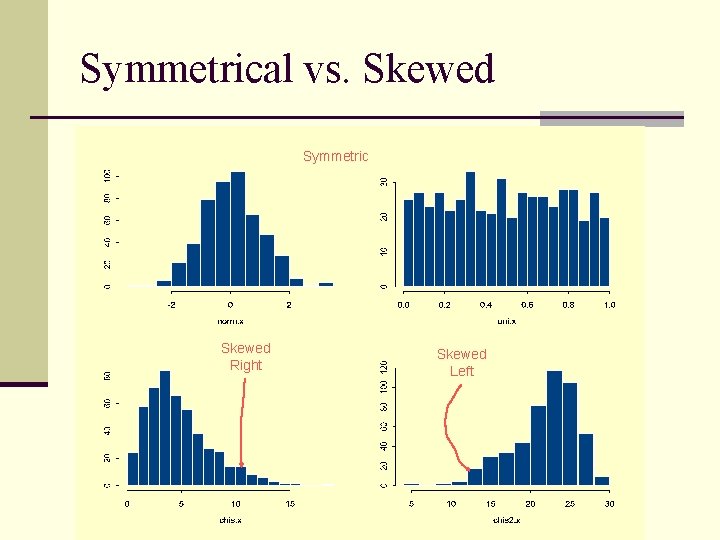
Symmetrical vs. Skewed Symmetric Skewed Right Skewed Left

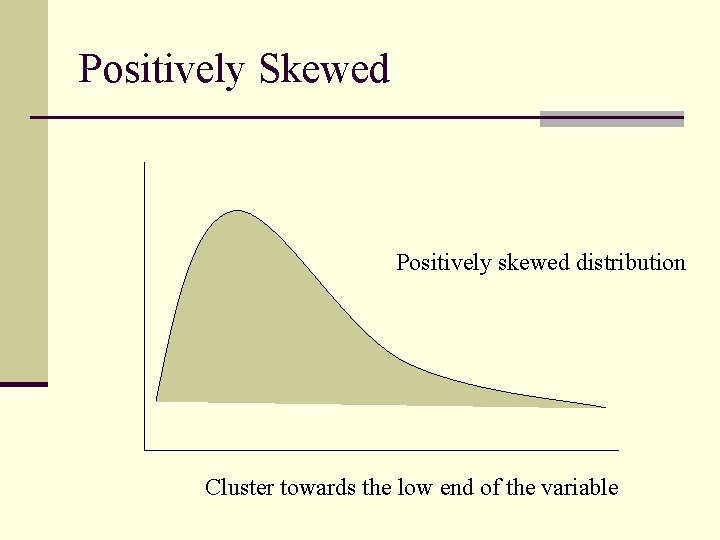
Positively Skewed Positively skewed distribution Cluster towards the low end of the variable

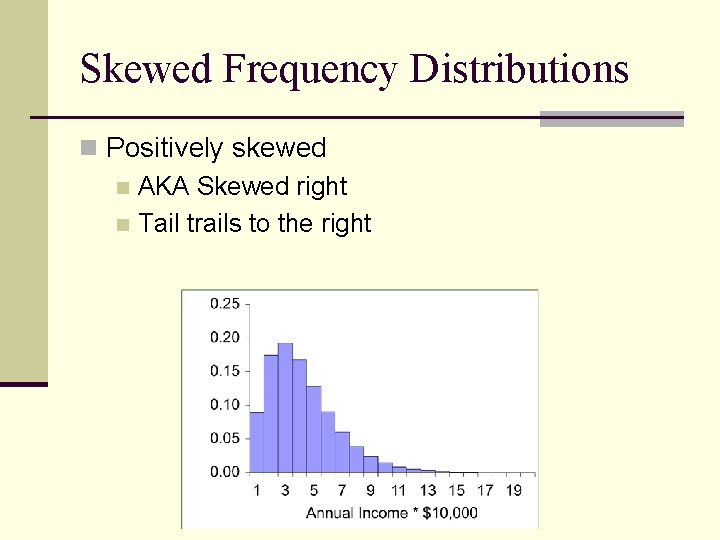
Skewed Frequency Distributions n Positively skewed n AKA Skewed right n Tail trails to the right

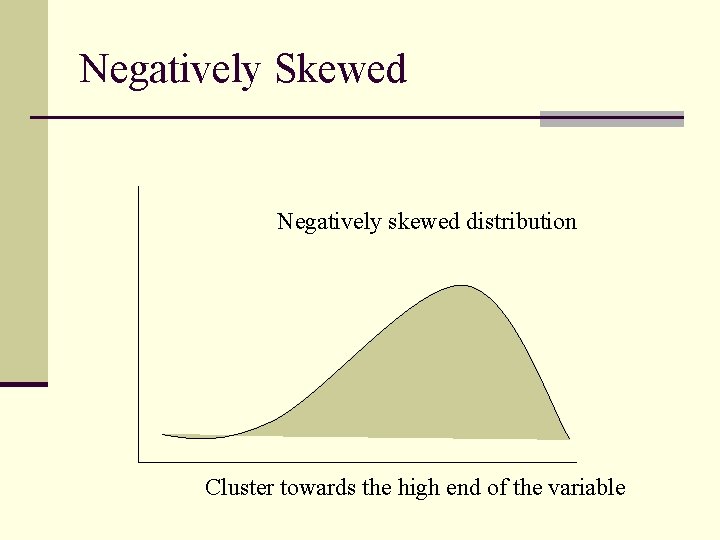
Negatively Skewed Negatively skewed distribution Cluster towards the high end of the variable

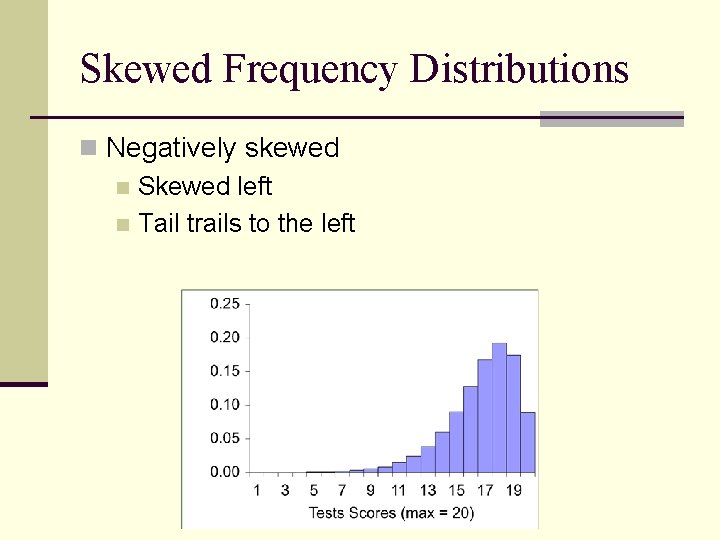
Skewed Frequency Distributions n Negatively skewed n Skewed left n Tail trails to the left

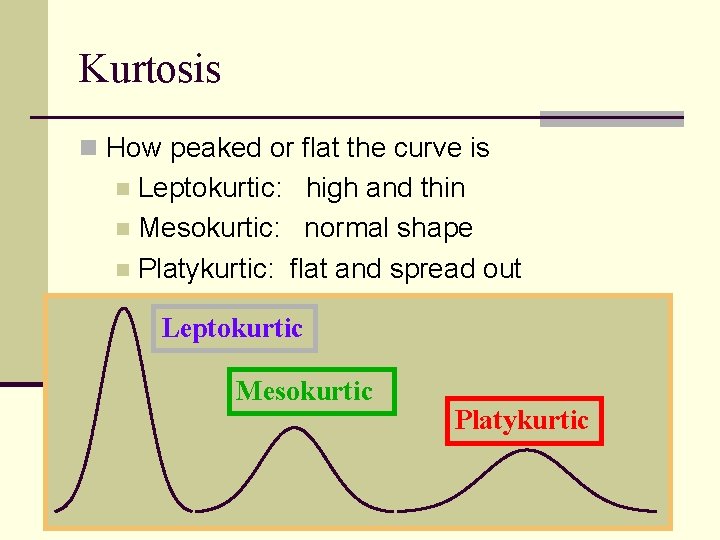
Kurtosis n How peaked or flat the curve is Leptokurtic: high and thin n Mesokurtic: normal shape n Platykurtic: flat and spread out n Leptokurtic Mesokurtic Platykurtic

Comparing the Kurtosis of Three Curves Curve A: Mesokurtic (Intermediate)

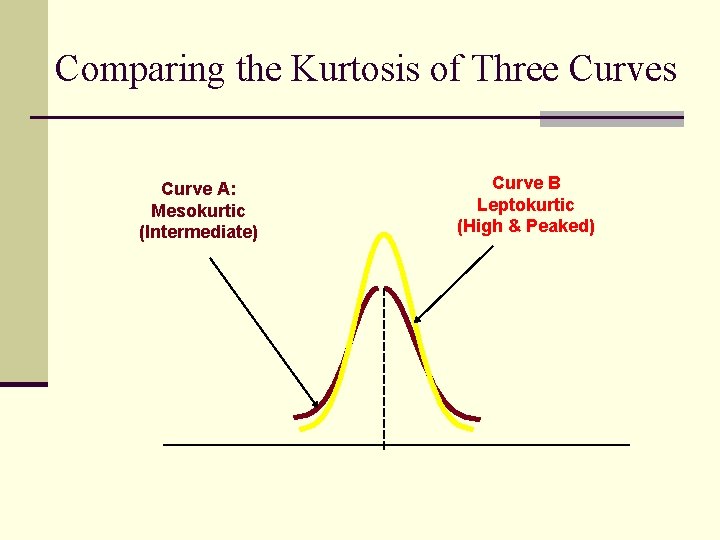
Comparing the Kurtosis of Three Curves Curve A: Mesokurtic (Intermediate) Curve B Leptokurtic (High & Peaked)

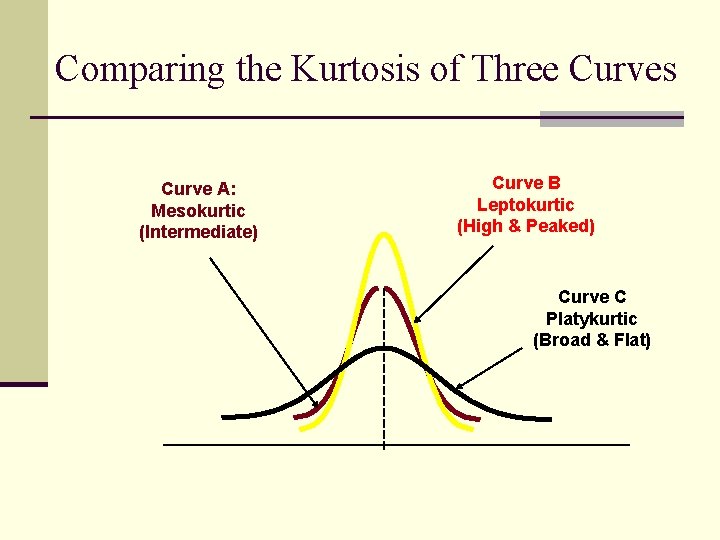
Comparing the Kurtosis of Three Curves Curve A: Mesokurtic (Intermediate) Curve B Leptokurtic (High & Peaked) Curve C Platykurtic (Broad & Flat)

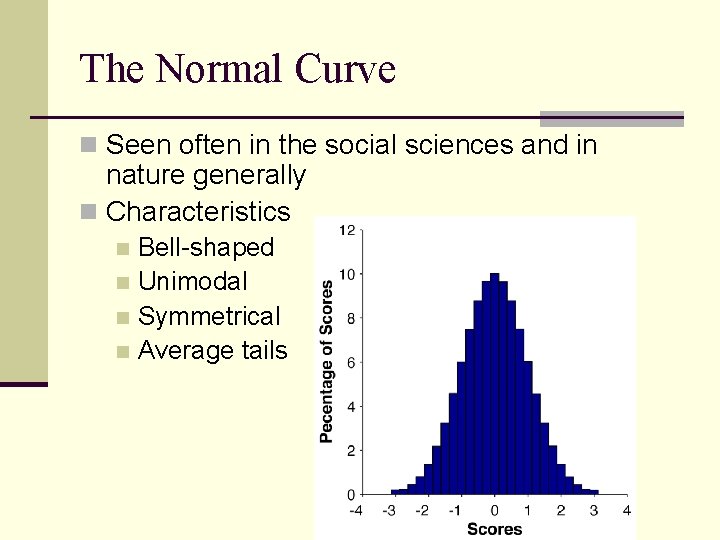
The Normal Curve n Seen often in the social sciences and in nature generally n Characteristics Bell-shaped n Unimodal n Symmetrical n Average tails n

Central Tendency n Give information concerning the average or typical score of a number of scores mean n median n mode n

Central Tendency: The Mean n The Mean is a measure of central tendency n What most people mean by “average” n Sum of a set of numbers divided by the number of numbers in the set

Central Tendency: The Mean n so if = the number of numbers in X (10 for this example) n then n. N

Central Tendency: The Mean n Important conceptual point: The mean is the balance point of the data in the sense that if we took each individual score (X) and subtracted the mean from them, some are positive and some are negative. If we add all of those up we will get zero. Also, the sum of the absolute values of the negative numbers is equal to the sum of the absolute values of the positive numbers

Central Tendency: The Median n Middlemost or most central item in the set of ordered numbers; it separates the distribution into two equal halves n If odd n, middle value of sequence if X = [1, 2, 4, 6, 9, 10, 12, 14, 17] n then 9 is the median n n If even n, average of 2 middle values n if X = [1, 2, 4, 6, 9, 10, 11, 12, 14, 17] n then 9. 5 is the median; i. e. , (9+10)/2 n Median is not affected by extreme values

Central Tendency: The Mode n The mode is the most frequently occurring number in a distribution if X = [1, 2, 4, 7, 7, 7, 8, 10, 12, 14, 17] n then 7 is the mode n n Mode is not affected by extreme values n There may be no mode or several modes

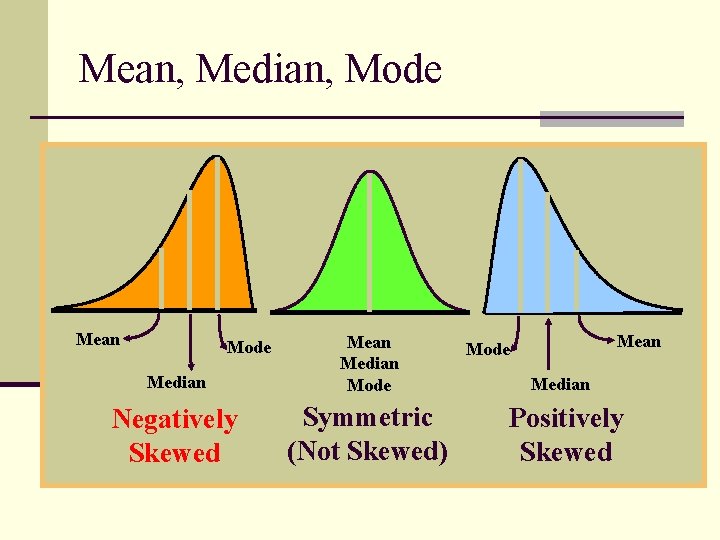
Mean, Median, Mode Mean Median Mode Negatively Skewed Symmetric (Not Skewed) Mode Mean Mode Median Positively Skewed

When to Use What n Mean is a great measure. But, there are time when its usage is inappropriate or impossible. Nominal data: Mode n The distribution is bimodal: Mode n You have ordinal data: Median or mode n Are a few extreme scores: Median n

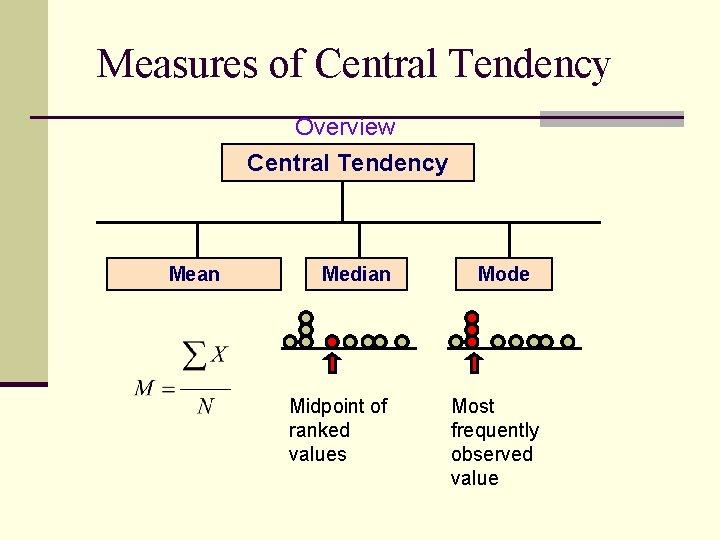
Measures of Central Tendency Overview Central Tendency Mean Median Midpoint of ranked values Mode Most frequently observed value

Variability n How tightly clustered or how widely dispersed the values are in a data set. n Example n Data set 1: [0, 25, 50, 75, 100] n Data set 2: [48, 49, 50, 51, 52] n Both have a mean of 50, but data set 1 clearly has greater Variability than data set 2.

Variability: The Range n The Range is one measure of variability n The range is the difference between the maximum and minimum values in a set n Example n n n Data set 1: [0, 25, 50, 75, 100]; R: 100 -0 = 100 Data set 2: [48, 49, 50, 51, 52]; R: 52 -48 = 4 The range ignores how data are distributed and only takes the extreme scores into account

Quartiles n Split Ordered Data into 4 Quarters 25% 25% n = first quartile n = second quartile= Median n = third quartile 25%

Variability: Interquartile Range n n Difference between third & first quartiles Interquartile Range = Q 3 - Q 1 n Spread in middle 50% n Not affected by extreme values

Variability: Standard Deviation n “The Standard Deviation tells us approximately how far the scores vary from the mean on average” The typical deviation in a given distribution

Variability: Standard Deviation n Standard Deviation can be calculated with the sum of squares (SS) divided by N

Variability: Standard Deviation n n let X = [3, 4, 5 , 6, 7] M=5 (X - M) = [-2, -1, 0, 1, 2] ñsubtract M from each number in X (X - M)2 = [4, 1, 0, 1, 4] ñsquared deviations from the mean S (X - M)2 = 10 ñ sum of squared deviations from the mean (SS) n S (X - M)2 /N = 10/5 = 2 ñ average squared deviation from the mean n S (X - M)2 /N = 2 = 1. 41 ñ square root of averaged squared deviation

Variability: Standard Deviation n n let X = [1, 3, 5, 7, 9] M=5 (X - M) = [-4, -2, 0, 2, 4 ] ñsubtract M from each number in X (X - M)2 = [16, 4, 0, 4, 16] ñsquared deviations from the mean S (X - M)2 = 40 ñ sum of squared deviations from the mean (SS) n S (X - M)2 /N = 40/5 = 8 ñ average squared deviation from the mean n S (X - M)2 /N = 8 = 2. 83 ñ square root of averaged squared deviation

Variability: Standard Deviation n The square of the standard deviation is called the variance Standard Deviation Variance

Standard Deviation & Standard Scores n Z scores are expressed in the following way n Z scores express how far a particular score is from the mean in units of standard deviation n if (X - M) = SD then (X - M)/SD = 1, and X is said to be one standard deviation above the mean

Standard Deviation & Standard Scores n Z scores provide a common scale to express deviations from a group mean

Standard Deviation and Standard Scores n Let’s say someone has an IQ of 145 and is 52 inches tall IQ in a population has a mean of 100 and a standard deviation of 15 n Height in a population has a mean of 64” with a standard deviation of 4 n n How many standard deviations is this person away from the average IQ? n How many standard deviations is this person away from the average height?