Numerical Differentiation 1 Numerical Differentiation First order derivatives

Numerical Differentiation 1

Numerical Differentiation First order derivatives p High order derivatives p. Examples p 2

Motivation How do you evaluate the derivative of a tabulated function. p How do we determine the velocity and acceleration from tabulated measurements. p Time (second) Displacement (meters) 0 30. 1 5 48. 2 10 50. 0 15 40. 2 3

Recall 4

For small values of h, the difference quotient [f (x 0 + h) − f (x 0)]/h can be used to approximate f’(x 0) with an error bounded by M|h|/2, where M is a bound on |f’’(x)| for x between x 0 and x 0 +h. CISE 301_Topic 6 5

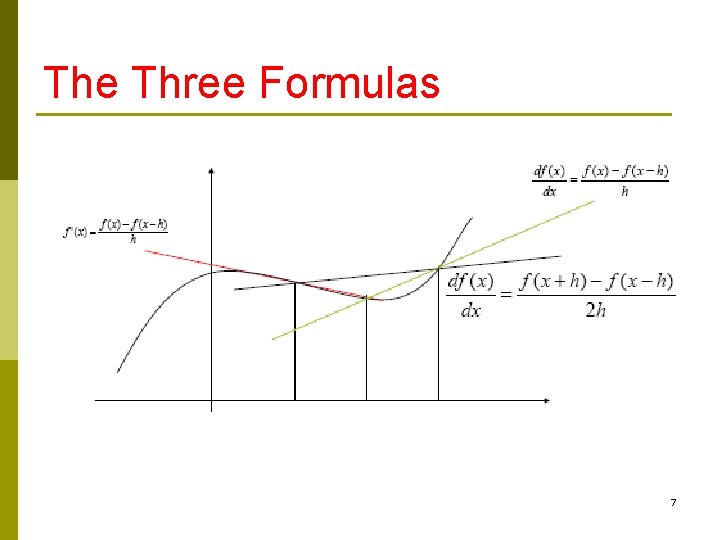
Three Formula 6

The Three Formulas 7

Forward/Backward Difference Formula 8

Central Difference Formula 9

The Three Formula (Revisited) 10

Higher Order Formulas 11

Other Higher Order Formulas 12

Example p Use forward, backward and centered difference approximations to estimate the first derivate of: f(x) = – 0. 1 x 4 – 0. 15 x 3 – 0. 5 x 2 – 0. 25 x + 1. 2 at x = 0. 5 using step size h = 0. 5 and h = 0. 25 p Note that the derivate can be obtained directly: f’(x) = – 0. 4 x 3 – 0. 45 x 2 – 1. 0 x – 0. 25 The true value of f’(0. 5) = -0. 9125 p In this example, the function and its derivate are known. However, in general, only tabulated data might be given. 13

Solution with Step Size = 0. 5 p p f(0. 5) = 0. 925, f(0) = 1. 2, f(1. 0) = 0. 2 Forward Divided Difference: f’(0. 5) (0. 2 – 0. 925)/0. 5 = -1. 45 | t| = |(-0. 9125+1. 45)/-0. 9125| = 58. 9% Backward Divided Difference: f’(0. 5) (0. 925 – 1. 2)/0. 5 = -0. 55 | t| = |(-0. 9125+0. 55)/-0. 9125| = 39. 7% Centered Divided Difference: f’(0. 5) (0. 2 – 1. 2)/1. 0 = -1. 0 | t| = |(-0. 9125+1. 0)/-0. 9125| = 9. 6% 14

Solution with Step Size = 0. 25 p p f(0. 5)=0. 925, f(0. 25)=1. 1035, f(0. 75)=0. 6363 Forward Divided Difference: f’(0. 5) (0. 6363 – 0. 925)/0. 25 = -1. 155 | t| = |(-0. 9125+1. 155)/-0. 9125| = 26. 5% Backward Divided Difference: f’(0. 5) (0. 925 – 1. 1035)/0. 25 = -0. 714 | t| = |(-0. 9125+0. 714)/-0. 9125| = 21. 7% Centered Divided Difference: f’(0. 5) (0. 6363 – 1. 1035)/0. 5 = -0. 934 | t| = |(-0. 9125+0. 934)/-0. 9125| = 2. 4% 15

Discussion p For both the Forward and Backward difference, the error is O(h) p Halving the step size h approximately halves the error of the Forward and Backward differences p The Centered difference approximation is more accurate than the Forward and Backward differences because the error is O(h 2) p Halving the step size h approximately quarters the error of the Centered difference. 16

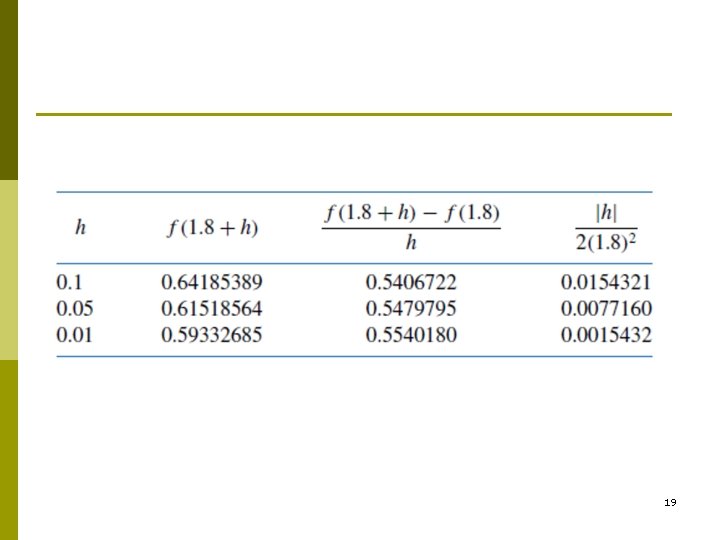
Example 2 Use the forward-difference formula to approximate the derivative of f (x) = ln x at x 0 = 1. 8 using h = 0. 1, h = 0. 05, and h = 0. 01, and determine bounds for the approximation errors. 17

Solution The forward-difference formula f (1. 8 + h) − f (1. 8) h with h = 0. 1 gives (ln 1. 9 − ln 1. 8)/0. 1 = (0. 64185389 − 0. 58778667)/0. 1 = 0. 5406722. Because f’’(x) = − 1/x 2 and 1. 8 < ξ < 1. 9, a bound for this approximation error is |hf’’(ξ )|/2 =|h|/2ξ 2 < 0. 1/2(1. 8)2 = 0. 0154321. 18

19