4 Numerical Methods Root Finding FixedPoint Iteration Successive

4 Numerical Methods Root Finding

Fixed-Point Iteration---- Successive Approximation Many problems also take on the specialized form: g(x)=x, where we seek, x, that satisfies this equation. In the limit, f(xk)=0, hence xk+1=xk f(x)=x g(x)

Fractals Images result when we deal with 2 dimensions. Such as complex numbers. Color indicates how quickly it converges or diverges.

Simple Fixed-Point Iteration Rearrange the function f(x)=0 so that x is on the left-hand side of the equation: x=g(x) Use the new function g to predict a new value of x - that is, xi+1=g(xi) The approximate error is given by:

Successive Approximations Begin Compute or choose initial object Compute next object Object sufficient? Yes End No

Fixed-point iterations

Example:

Iterative Solution Find the root of f(x) = e-x – x 1. Start with a guess say x 1=1, 2. Generate a) x 2=e-x 1 = e-1= 0. 368 b) x 3=e-x 2= e-0. 368 = 0. 692 c) x 4=e-x 3= e-0. 692=0. 500 In general: After a few more iteration we will get

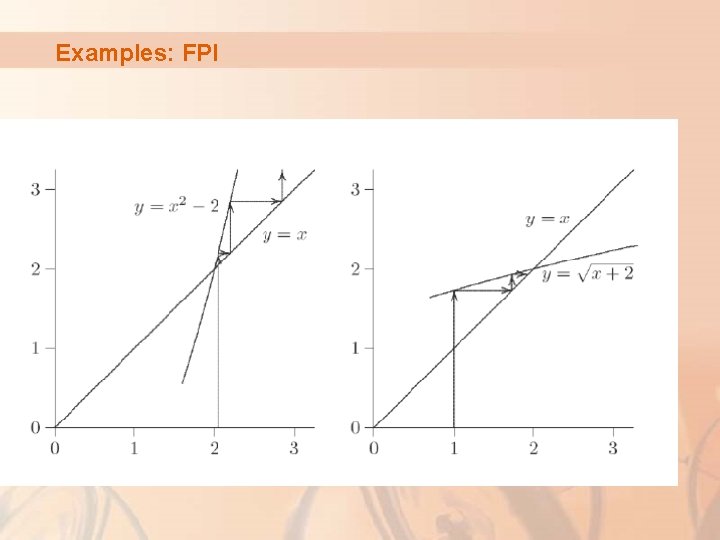
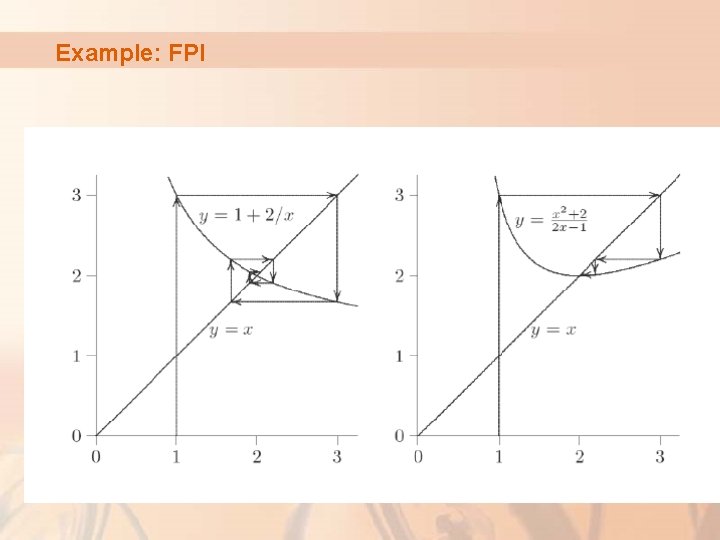
Problem Find a root near x=1. 0 and x=2. 0 Solution: § Starting at x=1, x=0. 292893 at 15 th iteration § Starting at x=2, it will not converge § Why? Relate to g'(x)=x. for convergence g'(x) < 1 § Starting at x=1, x=1. 707 at iteration 19 § Starting at x=2, x=1. 707 at iteration 12 § Why? Relate to

Examples

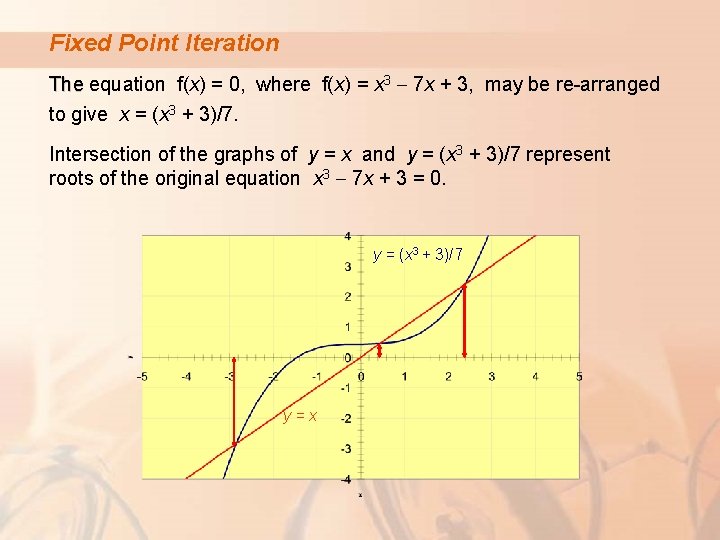
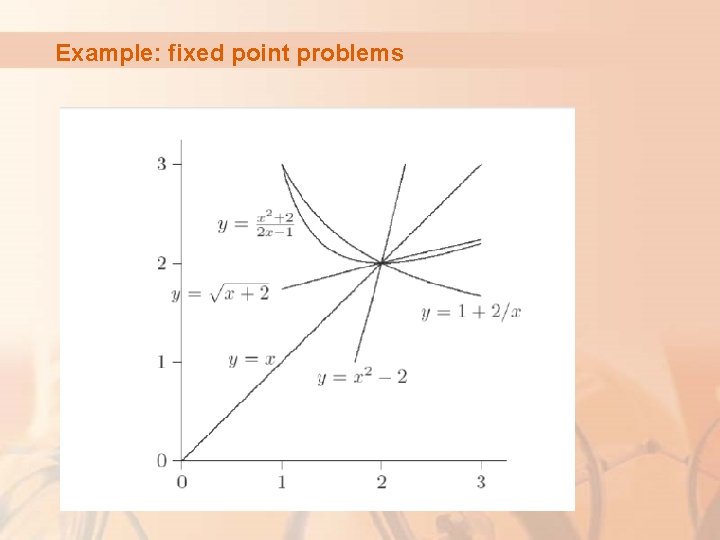
Fixed Point Iteration 3 - 7 x + 3, may be re-arranged The equation f(x) = 0, where f(x) = x The to give x = (x 3 + 3)/7. Intersection of the graphs of y = x and y = (x 3 + 3)/7 represent roots of the original equation x 3 - 7 x + 3 = 0. y = (x 3 + 3)/7 y = x

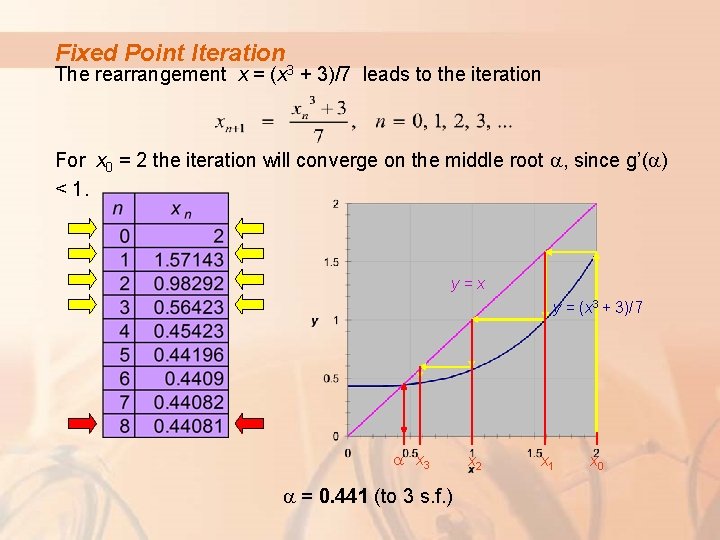
Fixed Point Iteration The rearrangement x = (x 3 + 3)/7 leads to the iteration To find the middle root a, let initial approximation x 0 = 2. etc. The iteration slowly converges to give a = 0. 441 (to 3 s. f. )

Fixed Point Iteration The rearrangement x = (x 3 + 3)/7 leads to the iteration For x 0 = 2 the iteration will converge on the middle root a, since g’(a) < 1. y = x y = (x 3 + 3)/7 a x 3 a = 0. 441 (to 3 s. f. ) x 2 x 1 x 0

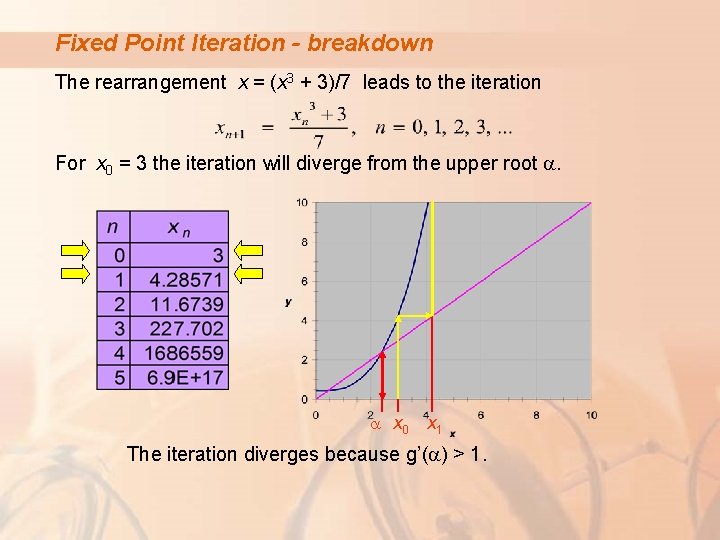
Fixed Point Iteration - breakdown The rearrangement x = (x 3 + 3)/7 leads to the iteration For x 0 = 3 the iteration will diverge from the upper root a. a x 0 x 1 The iteration diverges because g’(a) > 1.

Example: fixed point problems

Examples: FPI

Example: FPI

Convergence of FPI

Simple Fixed-Point Iteration Convergence

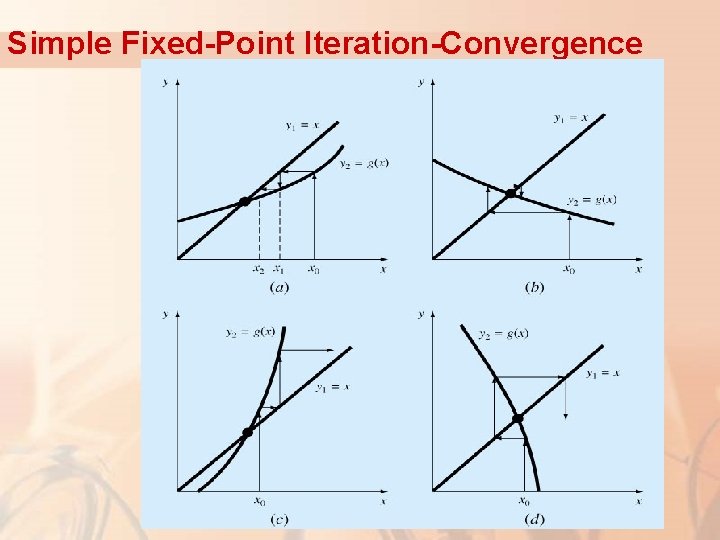
Simple Fixed-Point Iteration Convergence Fixed-point iteration converges if : • When the method converges, the error is roughly proportional to or less than the error of the previous step, therefore it is called “linearly convergent. ”

Simple Fixed-Point Iteration-Convergence

More on Convergence Graphically the solution is at the intersection of the two curves. We identify the point on y 2 corresponding to the initial guess and the next guess corresponds to the value of the argument x where y 1 (x) = y 2 (x). Convergence of the simple fixed-point iteration method requires that the derivative of g(x) near the root has a magnitude less than 1. a) b) c) d) Convergent, 0≤g’<1 Convergent, -1<g’≤ 0 Divergent, g’>1 Divergent, g’<-1 22

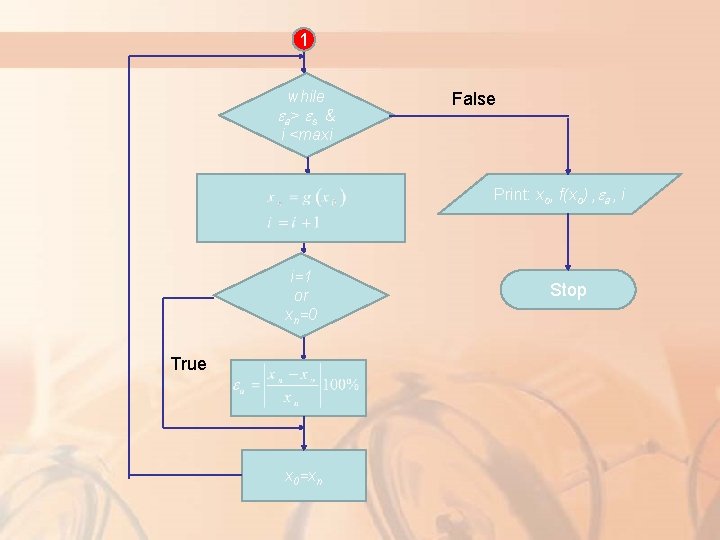
1 while a> s & i <maxi False Print: xo, f(xo) , a , i i=1 or xn=0 True x 0=xn Stop

Fixed Point Iteration 1. Use an initial guess x =1. 5 and y =3. 5 2. The iteration formulae: xi+1=(10 -xi 2)/yi and yi+1=57 -3 xiyi 2 3. First iteration, x=(10 -(1. 5)2)/3. 5=2. 21429 y=(57 -3(2. 21429)(3. 5)2=-24. 37516 4. Second iteration: x=(10 -2. 214292)/-24. 37516=-0. 209 y=57 -3(-0. 209)(-24. 37516)2=429. 709 5. Solution is diverging so try another iteration formula

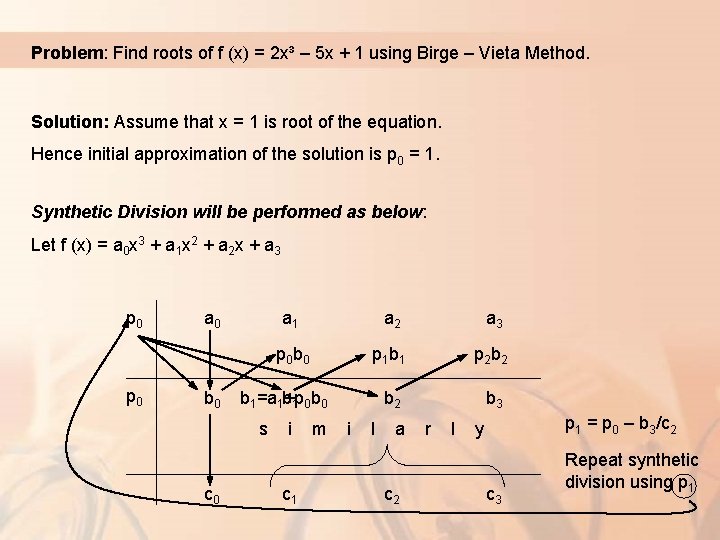
Birge – Vieta Method Used for finding roots of polynomial functions. Uses “synthetic division” of polynomial to extract factor of the given polynomial in the form of (x – p).

Problem: Find roots of f (x) = 2 x³ – 5 x + 1 using Birge – Vieta Method. Solution: Assume that x = 1 is root of the equation. Hence initial approximation of the solution is p 0 = 1. Synthetic Division will be performed as below: Let f (x) = a 0 x 3 + a 1 x 2 + a 2 x + a 3 p 0 a 0 b 0 a 1 a 2 a 3 p 0 b 0 p 1 b 1 p 2 b 2 b 3 b 1=a 1 b+p 1 0 b 0 p 1 = p 0 – b 3/c 2 s i m i l a r l y c 0 c 1 c 2 c 3 Repeat synthetic division using p 1

Birge-Vieta Method NR method with f(x) and f'(x) evaluated using Horner’s method Once a root is found, reduce order of polynomial

Iteration No. 1: 1 1 2 2 2 0 -5 1 2 2 -3 -2 2 4 1 -1 p 1 = p 0 – b 3/c 2 = 1 – (-2)/1 = 3 Iteration No. 2: 3 3 2 2 2 0 -5 1 6 18 39 6 13 40 6 36 147 12 49 187 p 2 = p 1 – b 3/c 2 = 3 – 40/49 = 2. 1837 Not required

Iteration No. 5: 1. 5185 2 2 2 0 -5 1 3. 037 4. 6117 -0. 5896 3. 037 -0. 3883 3. 037 9. 2234 6. 074 8. 8351 0. 4104 p 5 = p 4 – b 3/c 2 = 1. 5185 – 0. 4104/8. 8351 = 1. 4721 Iteration No. 6: 1. 4721 2 2 2 0 -5 1 2. 9442 4. 3342 -0. 9801 2. 9442 -0. 6658 0. 01986 2. 9442 8. 6683 5. 8884 8. 0025 p 6 = p 5 – b 3/c 2 = 1. 4721 – 0. 01986/8. 0025 = 1. 469624

the equation x 3+x 2 -3 x-3 using Birge-Vieta Method where x 0 = 2. Using the synthetic division, 2|1 -3 | 2 6 |1 3 3¬f(x 0) | 2 10 |1 5 13¬f ’(x 0) Now, x 1 = 2 – 3/13 = 1. 7692

Examples Determine the lowest positive root of: f(x) = 8 e-x sin (x) - 1 Using the Newton-Raphson method (three iterations, x 0 = 0. 3) and Using the secant method (four iterations, x-1 = 0. 5 and x 0 = 0. 4). Using the modified secant method (three iterations, x 0 = 0. 3, d = 0. 01).

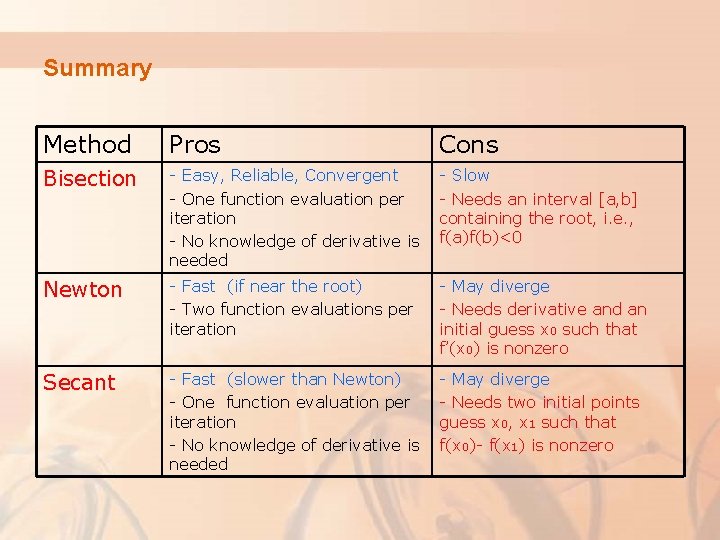
Summary Method Pros Cons Bisection - Easy, Reliable, Convergent - One function evaluation per iteration - No knowledge of derivative is needed - Slow - Needs an interval [a, b] containing the root, i. e. , f(a)f(b)<0 Newton - Fast (if near the root) - Two function evaluations per iteration - May diverge - Needs derivative and an initial guess x 0 such that f’(x 0) is nonzero Secant - Fast (slower than Newton) - One function evaluation per iteration - No knowledge of derivative is needed - May diverge - Needs two initial points guess x 0, x 1 such that f(x 0)- f(x 1) is nonzero