Numerical Descriptive Techniques 1 Summary Measures Describing Data

Numerical Descriptive Techniques 1

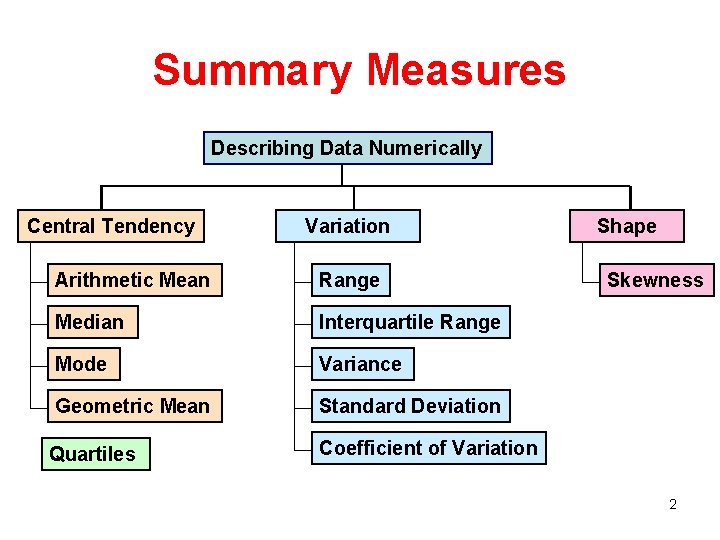
Summary Measures Describing Data Numerically Central Tendency Variation Arithmetic Mean Range Median Interquartile Range Mode Variance Geometric Mean Standard Deviation Quartiles Coefficient of Variation Shape Skewness 2

Measures of Central Location • Usually, we focus our attention on two types of measures when describing population characteristics: – Central location – Variability or spread The measure of central location reflects the locations of all the actual data points. 3

Measures of Central Location • The measure of central location reflects the locations of all the actual data points. • How? With two data points, the central location But if the third data point With one data point should fall in the middle appears on the left hand-side clearly the central between them (in order of the midrange, it should “pull” location is at the point to reflect the location of the central location to the left. itself. both of them). 4

The Arithmetic Mean • This is the most popular and useful measure of central location Sum of the observations Mean = Number of observations 5

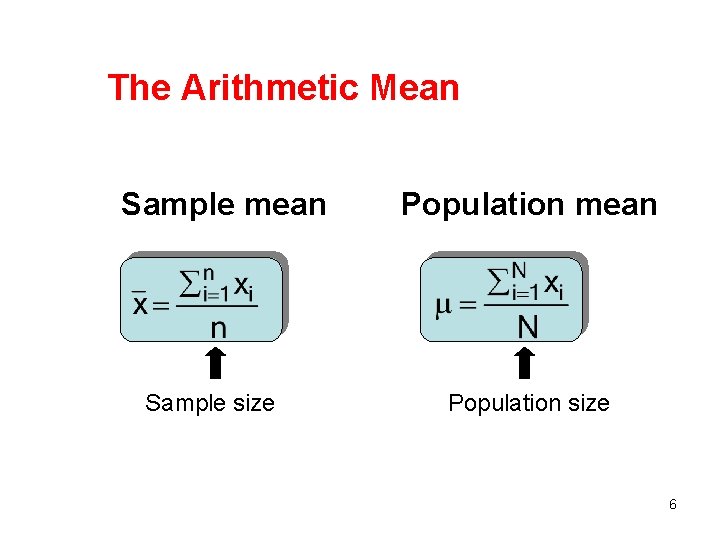
The Arithmetic Mean Sample mean Sample size Population mean Population size 6

The Arithmetic Mean • Example 1 The reported time on the Internet of 10 adults are 0, 7, 12, 5, 33, 14, 8, 0, 9, 22 hours. Find the mean time on the Internet. 0 7 22 11. 0 • Example 2 Suppose the telephone bills represent the population of meas The population mean is 42. 19 38. 45 45. 77 43. 59 7

The Arithmetic Mean • Drawback of the mean: It can be influenced by unusual observations, because it uses all the information in the data set. 8

The Median • The Median of a set of observations is the value that falls in the middle when the observations are arranged in order of magnitude. It divides the data in half. Example 3 Comment Suppose only 9 adults were sampled Find the median of the time on the internet (exclude, say, the longest time (33)) for the 10 adults of example 1 Odd number of observations Even number of observations 0, 0, 5, 5, 7, 7, 8, 8, , 9, 12, 14, 22, 33 0, 330, 5, 7, 8 8 9, 12, 14, 229 8. 5

The Median • Median of 8 2 9 11 1 6 3 n = 7 (odd sample size). First order the data. 1 2 3 6 8 9 11 Median • For odd sample size, median is the {(n+1)/2}th ordered observation. 10

The Median • The engineering group receives e-mail requests for technical information from sales and services person. The daily numbers for 6 days were 11, 9, 17, 19, 4, and 15. What is the central location of the data? • For even sample sizes, the median is the average of {n/2}th and {n/2+1}th ordered observations. 11

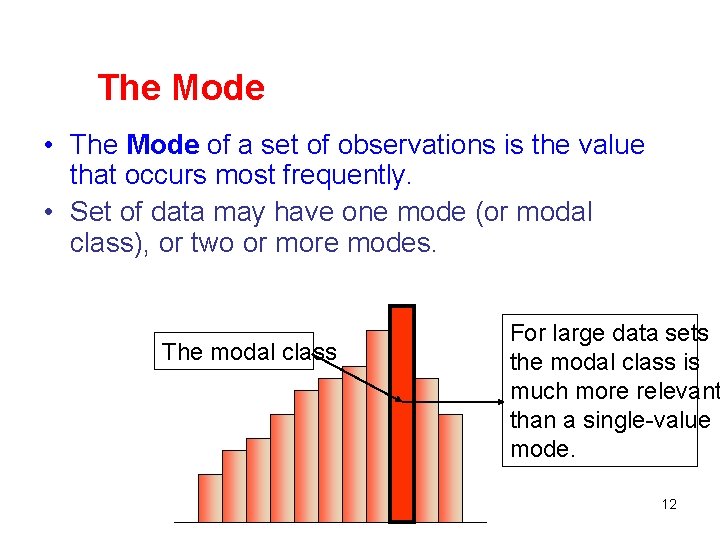
The Mode • The Mode of a set of observations is the value that occurs most frequently. • Set of data may have one mode (or modal class), or two or more modes. The modal class For large data sets the modal class is much more relevant than a single-value mode. 12

The Mode • Find the mode for the data in Example 1. Here are the data again: 0, 7, 12, 5, 33, 14, 8, 0, 9, 22 Solution • All observation except “ 0” occur once. There are two “ 0”. Thus, the mode is zero. • Is this a good measure of central location? • The value “ 0” does not reside at the center of this set (compare with the mean = 11. 0 and the median = 8. 5). 13

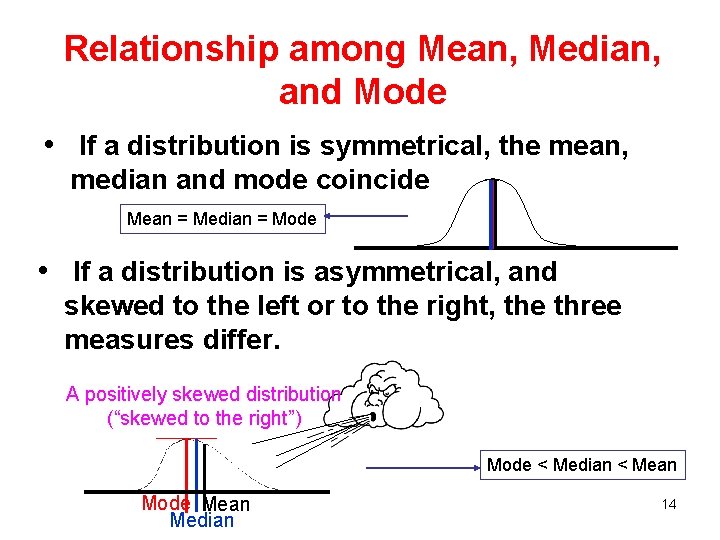
Relationship among Mean, Median, and Mode • If a distribution is symmetrical, the mean, median and mode coincide Mean = Median = Mode • If a distribution is asymmetrical, and skewed to the left or to the right, the three measures differ. A positively skewed distribution (“skewed to the right”) Mode < Median < Mean Mode Mean Median 14

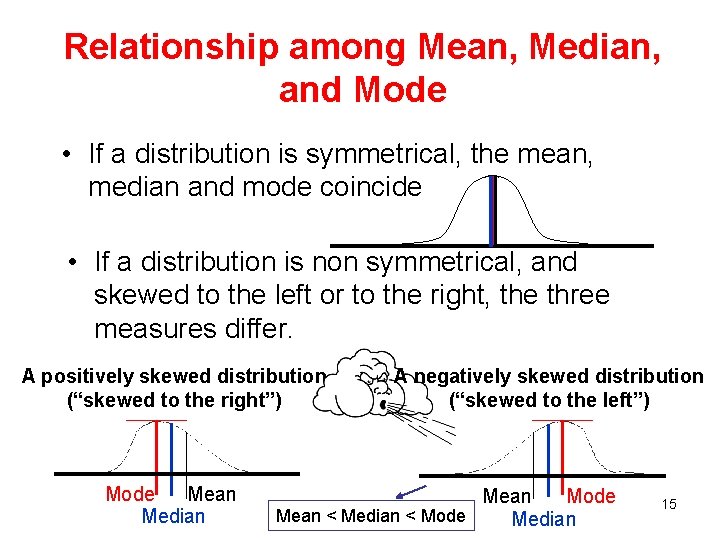
Relationship among Mean, Median, and Mode • If a distribution is symmetrical, the mean, median and mode coincide • If a distribution is non symmetrical, and skewed to the left or to the right, the three measures differ. A positively skewed distribution (“skewed to the right”) Mode Mean Median A negatively skewed distribution (“skewed to the left”) Mean Mode Mean < Median < Mode Median 15

Geometric Mean • The arithmetic mean is the most popular measure of the central location of the distribution of a set of observations. • But the arithmetic mean is not a good measure of the average rate at which a quantity grows over time. That quantity, whose growth rate (or rate of change) we wish to measure, might be the total annual sales of a firm or the market value of an investment. • The geometric mean should be used to measure the average growth rate of the values of a variable over time. 16

17

Example 18

19

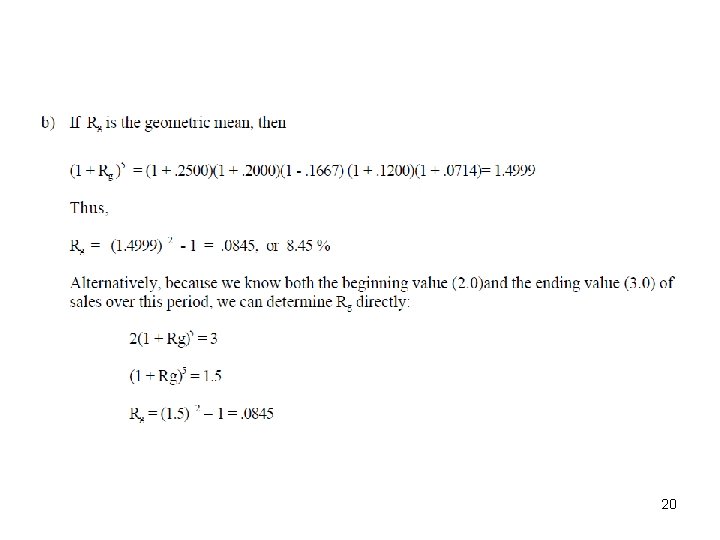
20

21

Measures of variability • Measures of central location fail to tell the whole story about the distribution. • A question of interest still remains unanswered: How much are the observations spread out around the mean value? 22

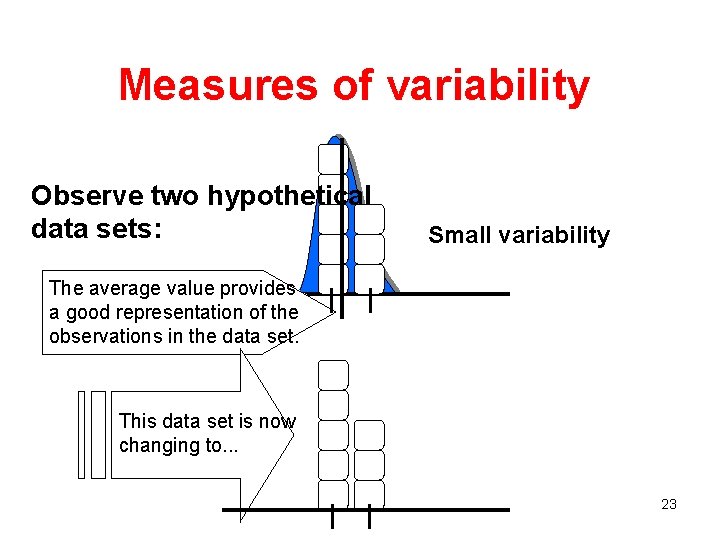
Measures of variability Observe two hypothetical data sets: Small variability The average value provides a good representation of the observations in the data set. This data set is now changing to. . . 23

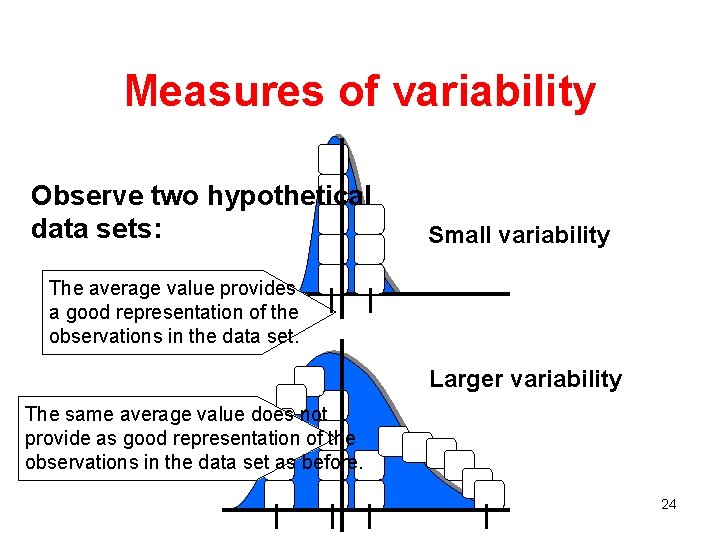
Measures of variability Observe two hypothetical data sets: Small variability The average value provides a good representation of the observations in the data set. Larger variability The same average value does not provide as good representation of the observations in the data set as before. 24

The range – The range of a set of observations is the difference between the largest and smallest observations. – Its major advantage is the ease with which it can be computed. – Its major shortcoming is its failure to provide information on the dispersion of the observations between the two end points. But, how do all the observations spread out? The range cannot assist in answering this question ? Range ? ? Smallest observation Largest observation 25

The Variance l l l This measure reflects the dispersion of all the observations The variance of a population of size N, x 1, x 2, …, x. N whose mean is m is defined as The variance of a sample of n observations x 1, x 2, …, xn whose mean is defined as 26

Why not use the sum of deviations? Consider two small populations: 9 -10= -1 11 -10= +1 8 -10= -2 A measure of dispersion A B 4 Can the sum of deviations Should agrees with this Be a good measure of dispersion? The sum of deviations observation. is zero for both populations, 8 9 10 therefore, 11 12 is not …but measurements in B a The mean of both good measure are more dispersed populations is 10. . . of dispersion. than those in A. 7 10 13 12 -10= +2 Sum = 0 4 -10 = - 6 16 -10 = +6 7 -10 = -3 16 13 -10 = +3 27 Sum = 0

The Variance Let us calculate the variance of the two popula Why is the variance defined as After all, the sum of squared the average squared deviation? deviations increases in Why not use the sum of squared magnitude when the variation deviations as a measure of of a data set increases!! 28 variation instead?

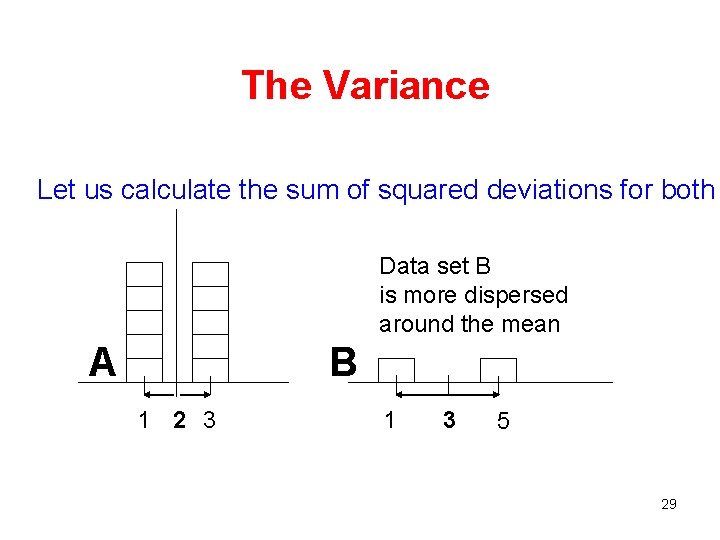
The Variance Let us calculate the sum of squared deviations for both Which data set has a larger dispersion? Data set B is more dispersed around the mean A B 1 2 3 1 3 5 29

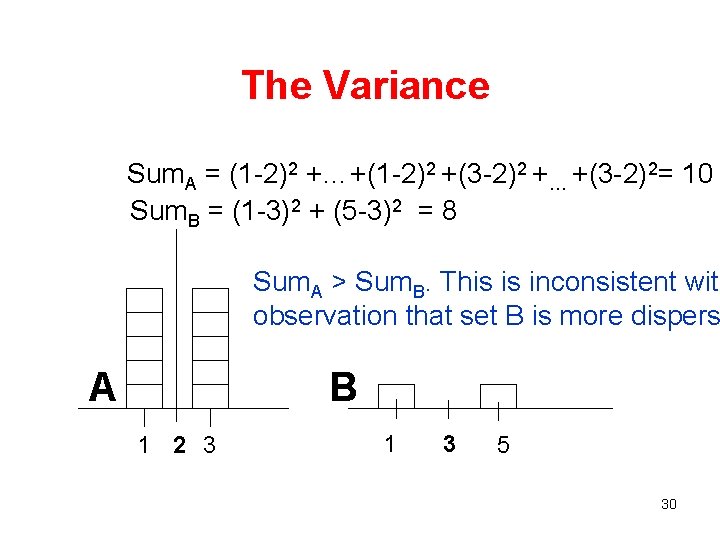
The Variance Sum. A = (1 -2)2 +…+(1 -2)2 +(3 -2)2 +… +(3 -2)2= 10 Sum. B = (1 -3)2 + (5 -3)2 = 8 Sum. A > Sum. B. This is inconsistent with observation that set B is more dispers A B 1 2 3 1 3 5 30

The Variance However, when calculated on “per observation” basis (variance), the data set dispersions are properly ranked. s. A 2 = Sum. A/N = 10/10 = 1 s. B 2 = Sum. B/N = 8/2 = 4 A B 1 2 3 1 3 5 31

The Variance • Example 4 – The following sample consists of the number of jobs six students applied for: 17, 15, 23, 7, 9, 13. Find its mean and variance • Solution 32

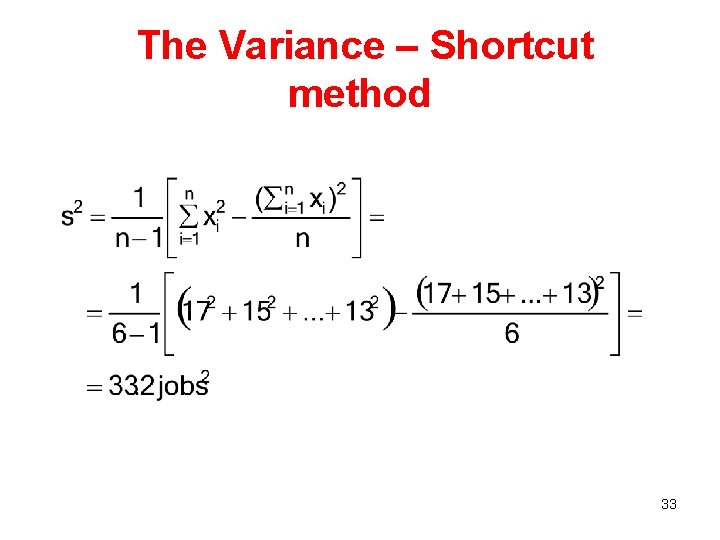
The Variance – Shortcut method 33

Standard Deviation • The standard deviation of a set of observations is the square root of the variance. 34

Standard Deviation • Example 5 – To examine the consistency of shots for a new innovative golf club, a golfer was asked to hit 150 shots, 75 with a currently used (7 -iron) club, and 75 with the new club. – The distances were recorded. – Which 7 -iron is more consistent? 35

Standard Deviation • Example 5 – solution Excel printout, from the “Descriptive Statistics” sub-menu. The innovation club is more consistent, and because the means are close, is considered a better club 36

Interpreting Standard Deviation • The standard deviation can be used to – compare the variability of several distributions – make a statement about the general shape of a distribution. • The empirical rule: If a sample of observations has a mound-shaped distribution, the interval 37

Interpreting Standard Deviation • Example 6 A statistics practitioner wants to describe the way returns on investment are distributed. – The mean return = 10% – The standard deviation of the return = 8% – The histogram is bell shaped. 38

Interpreting Standard Deviation Example 6 – solution • The empirical rule can be applied (bell shaped histogram) • Describing the return distribution – Approximately 68% of the returns lie between 2% and 18% [10 – 1(8), 10 + 1(8)] – Approximately 95% of the returns lie between -6% and 26% [10 – 2(8), 10 + 2(8)] – Approximately 99. 7% of the returns lie between -14% and 34% [10 – 3(8), 10 + 3(8)] 39

The Chebyshev’s Theorem • For any value of k 1, greater than 100(1 -1/k 2)% of the data lie within the interval from to . • This theorem is valid for any set of measurements (sample, population) of any shape!! k Interval Chebyshev Empirical Rule 1 2 3 at least 0% (1 -1/12) approximately 68% ) at least 75%(1 -1/22 approximately 95% ) at least 89%(1 -1/32 approximately 99. 7% 40

The Chebyshev’s Theorem • Example 7 – The annual salaries of the employees of a chain of computer stores produced a positively skewed histogram. The mean and standard deviation are $28, 000 and $3, 000, respectively. What can you say about the salaries at this chain? Solution At least 75% of the salaries lie between $22, 000 and $34, 000 28000 – 2(3000) 28000 + 2(3000) At least 88. 9% of the salaries lie between $$19, 000 and $37, 000 41 28000 – 3(3000) 28000 + 3(3000)

The Coefficient of Variation • The coefficient of variation of a set of measurements is the standard deviation divided by the mean value. • This coefficient provides a proportionate measure of variation. A standard deviation of 10 may be perceived large when the mean value is 100, but only moderately large when the mean value is 500 42

Sample Percentiles and Box Plots • Percentile – The pth percentile of a set of measurements is the value for which • p percent of the observations are less than that value • 100(1 -p) percent of all the observations are greater than that value. – Example • Suppose your score is the 60% percentile of a SAT test. Then 60% of all the scores lie here Your score 40% 43

Sample Percentiles • To determine the sample 100 p percentile of a data set of size n, determine a) At least np of the values are less than or equal to it. b) At least n(1 -p) of the values are greater than or equal to it. • Find the 10 percentile of 6 8 3 6 2 8 1 • Order the data: 1 2 3 6 6 8 • Find np and n(1 -p): 7(0. 10) = 0. 70 and 7(1 -0. 10) = 6. 3 A data value such that at least 0. 7 of the values are less than or equal to it 44 and at least 6. 3 of the values greater than or equal to it. So, the first observation is the 10 percentile.

Quartiles • Commonly used percentiles – First (lower)decile = 10 th percentile – First (lower) quartile, Q 1 = 25 th percentile – Second (middle)quartile, Q 2 = 50 th percentile – Third quartile, Q 3 = 75 th percentile – Ninth (upper)decile = 90 th percentile 45

Quartiles • Example 8 Find the quartiles of the following set of measurements 7, 8, 12, 17, 29, 18, 4, 27, 30, 2, 4, 10, 21, 5, 8 46

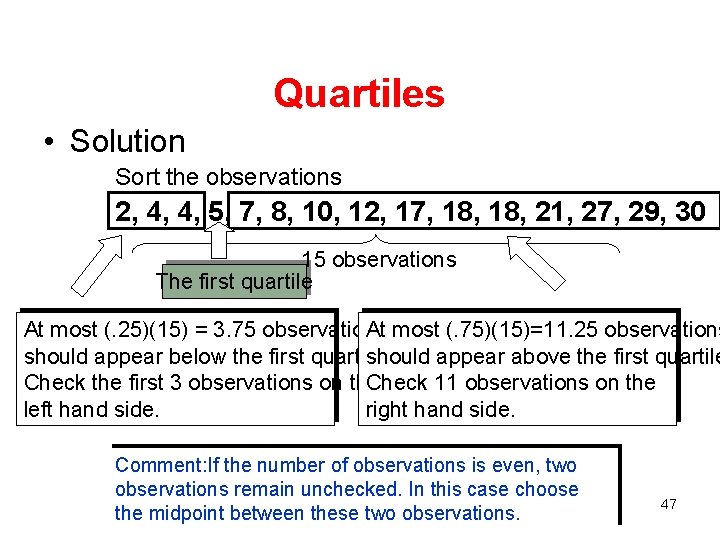
Quartiles • Solution Sort the observations 2, 4, 4, 5, 7, 8, 10, 12, 17, 18, 21, 27, 29, 30 15 observations The first quartile At most (. 25)(15) = 3. 75 observations At most (. 75)(15)=11. 25 observations should appear below the first quartile. should appear above the first quartile Check the first 3 observations on the Check 11 observations on the left hand side. right hand side. Comment: If the number of observations is even, two observations remain unchecked. In this case choose the midpoint between these two observations. 47

Location of Percentiles • Find the location of any percentile using the formula • Example 9 Calculate the 25 th, 50 th, and 75 th percentile of the data in Example 1 48

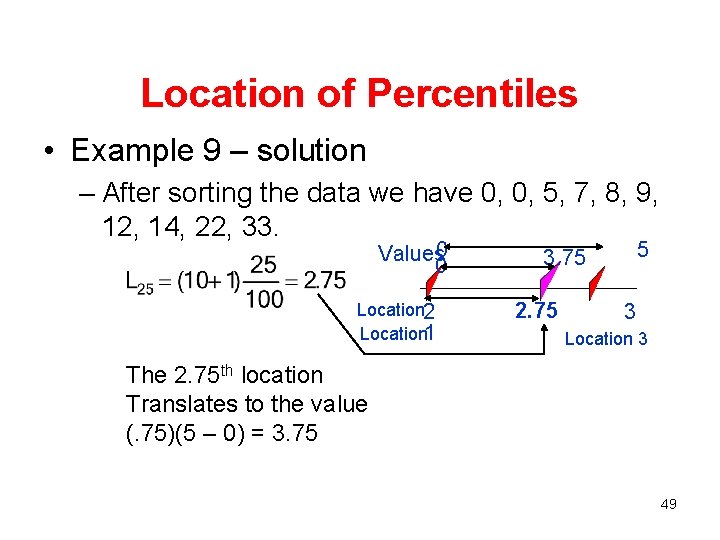
Location of Percentiles • Example 9 – solution – After sorting the data we have 0, 0, 5, 7, 8, 9, 12, 14, 22, 33. Values 0 5 3. 75 0 Location 2 3 2. 75 Location 1 Location 3 The 2. 75 th location Translates to the value (. 75)(5 – 0) = 3. 75 49

Location of Percentiles • Example 9 – solution continued The 50 th percentile is halfway between the fifth and sixth observations (in the middle between 8 and 9), that is 8. 5. 50

Location of Percentiles • Example 9 – solution continued The 75 th percentile is one quarter of the distance between the eighth and ninth observation that is 14+. 25(22 – 14) = 16. Eighth Ninth observation 51

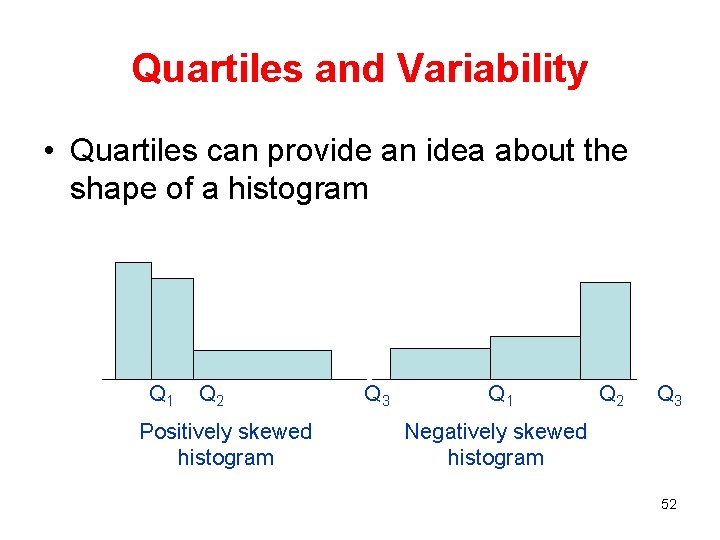
Quartiles and Variability • Quartiles can provide an idea about the shape of a histogram Q 1 Q 2 Q 3 Positively skewed histogram Q 1 Q 2 Q 3 Negatively skewed histogram 52

Interquartile Range • This is a measure of the spread of the middle 50% of the observations • Large value indicates a large spread of the observations Interquartile range = Q 3 – Q 1 53

Box Plot – This is a pictorial display that provides the main descriptive measures of the data set: • • • L - the largest observation Q 3 - The upper quartile Q 2 - The median Q 1 - The lower quartile S - The smallest observation 1. 5(Q 3 – Q 1) Whisker S Q 1 1. 5(Q 3 – Q 1) Q 2 Q 3 Whisker L 54

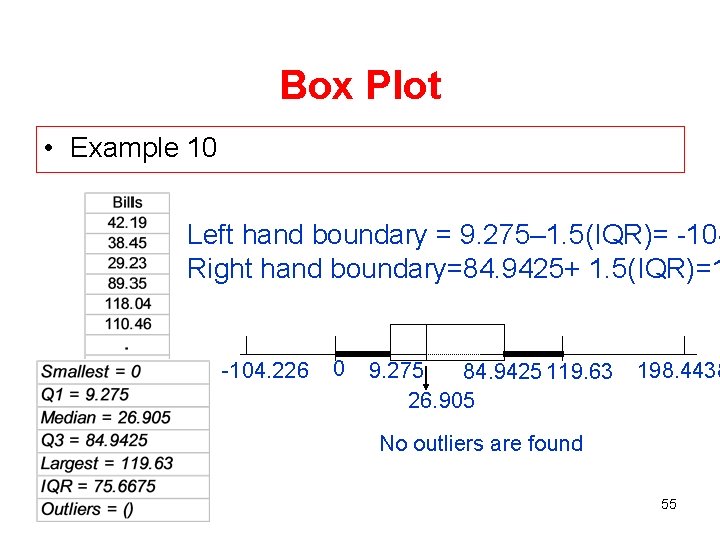
Box Plot • Example 10 Left hand boundary = 9. 275– 1. 5(IQR)= -104 Right hand boundary=84. 9425+ 1. 5(IQR)=1 -104. 226 0 9. 275 84. 9425 119. 63 26. 905 198. 4438 No outliers are found 55

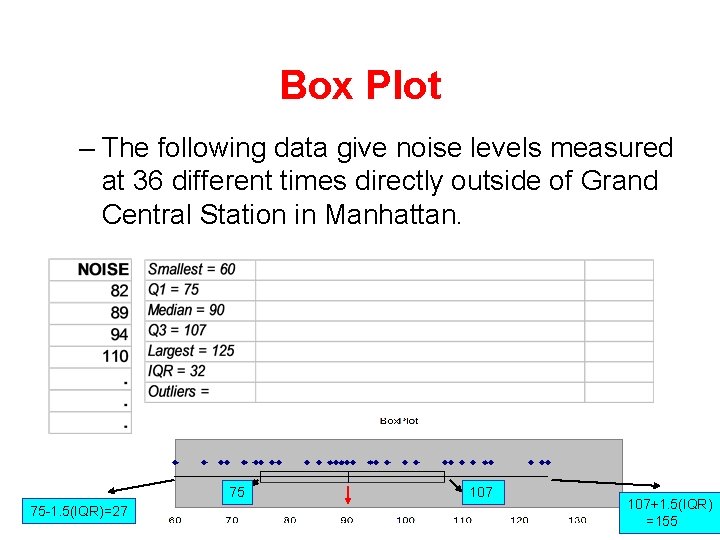
Box Plot – The following data give noise levels measured at 36 different times directly outside of Grand Central Station in Manhattan. 75 75 -1. 5(IQR)=27 107 56 107+1. 5(IQR) =155

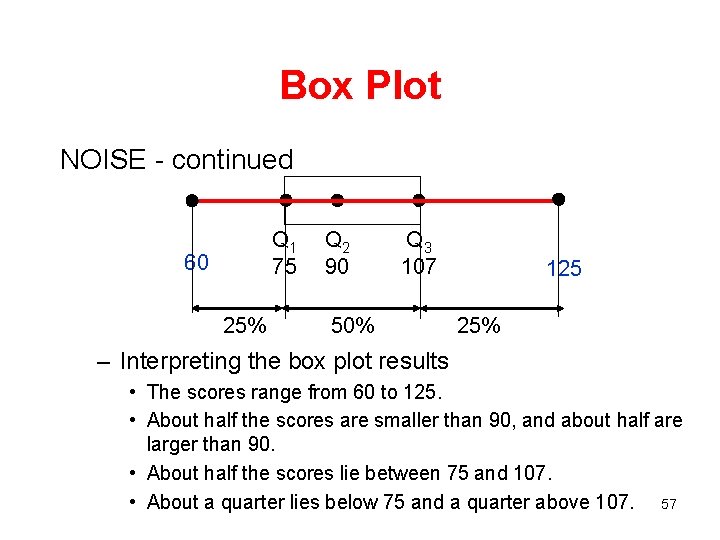
Box Plot NOISE - continued Q 1 75 60 25% Q 2 90 Q 3 107 50% 125 25% – Interpreting the box plot results • The scores range from 60 to 125. • About half the scores are smaller than 90, and about half are larger than 90. • About half the scores lie between 75 and 107. • About a quarter lies below 75 and a quarter above 107. 57

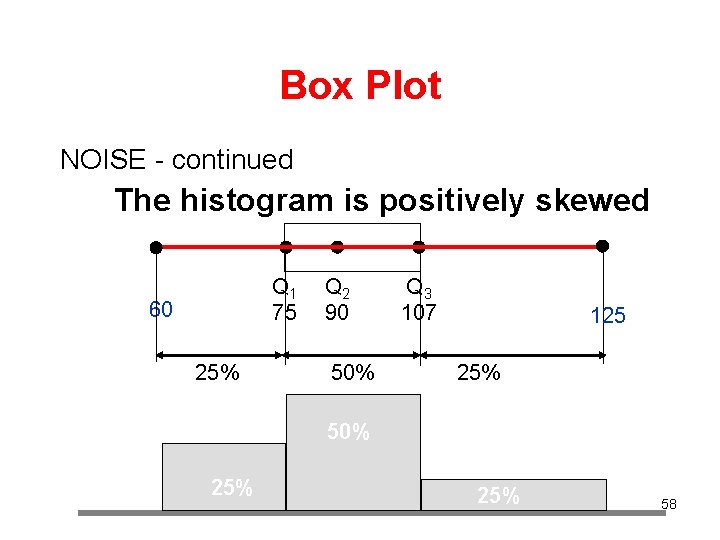
Box Plot NOISE - continued The histogram is positively skewed Q 1 75 60 25% Q 2 90 50% Q 3 107 125 25% 50% 25% 58

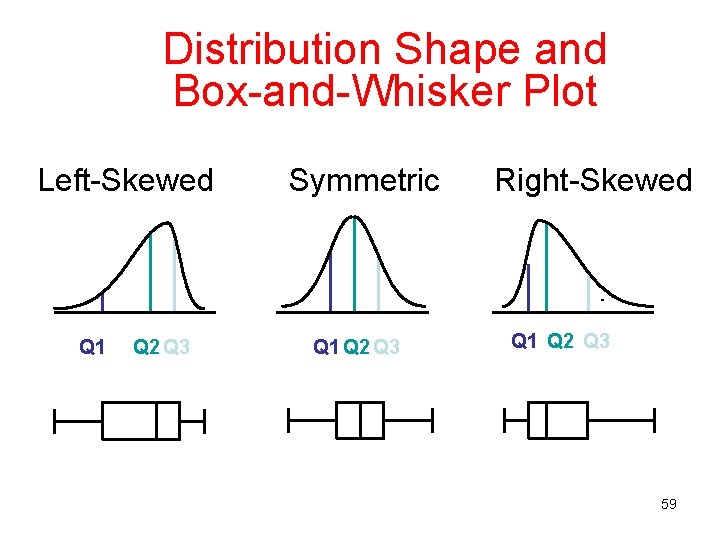
Distribution Shape and Box-and-Whisker Plot Left-Skewed Q 1 Q 2 Q 3 Symmetric Q 1 Q 2 Q 3 Right-Skewed Q 1 Q 2 Q 3 59

Box Plot • Example 11 – A study was organized to compare the quality of service in 5 drive through restaurants. – Interpret the results • Example 11 – solution – Minitab box plot 60

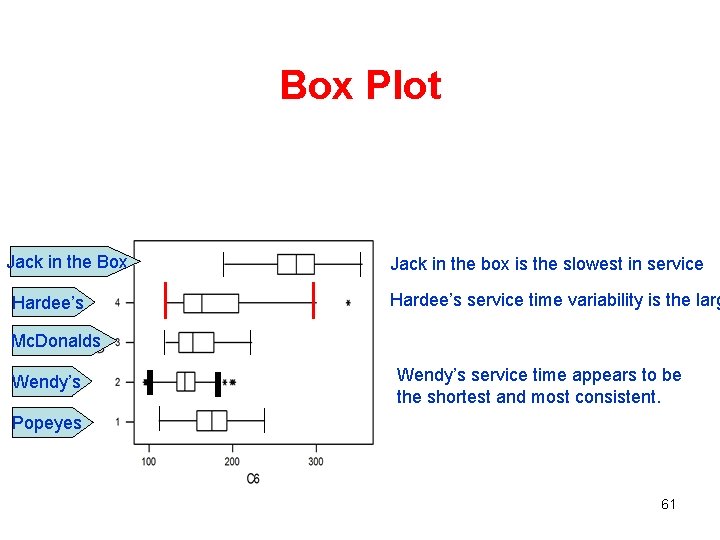
Box Plot Jack in the Box Hardee’s Jack in the box is the slowest in service Hardee’s service time variability is the larg Mc. Donalds Wendy’s service time appears to be the shortest and most consistent. Popeyes 61

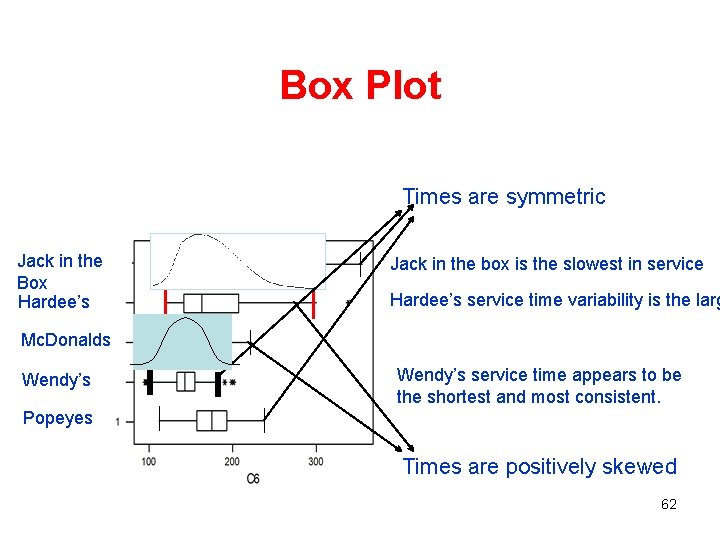
Box Plot Times are symmetric Jack in the Box Hardee’s Jack in the box is the slowest in service Hardee’s service time variability is the larg Mc. Donalds Wendy’s service time appears to be the shortest and most consistent. Popeyes Times are positively skewed 62

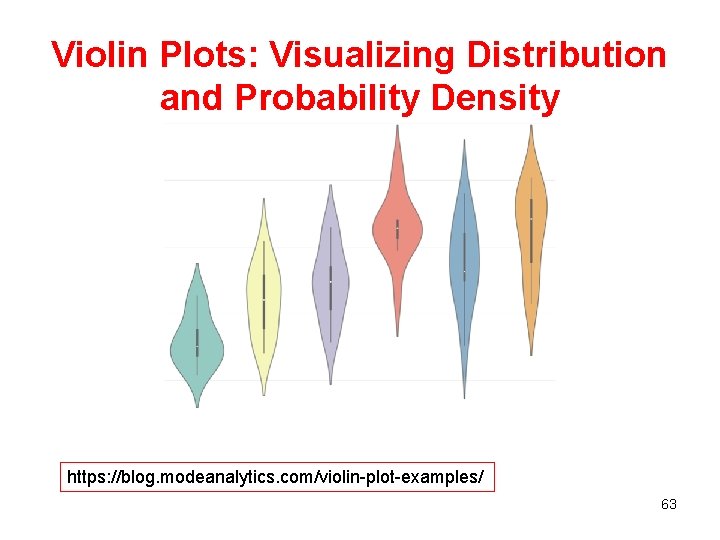
Violin Plots: Visualizing Distribution and Probability Density https: //blog. modeanalytics. com/violin-plot-examples/ 63

VIOLIN PLOTS • A Violin Plot is used to visualize the distribution of the data and its probability density. • This chart is a combination of a Box Plot and a Kernel Density Plot that is rotated and placed on each side, to show the distribution shape of the data. • Box Plots are limited in their display of the data, as their visual simplicity tends to hide significant details about how values in the data are distributed. For example, with Box Plots you can't see if the distribution is bimodal or multimodal. While Violin plots display more information, they can be more noisier than a Box Plot. 64

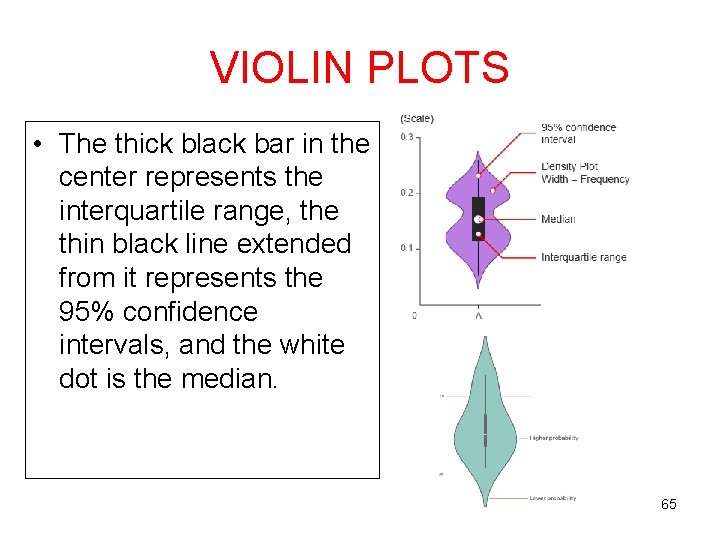
VIOLIN PLOTS • The thick black bar in the center represents the interquartile range, the thin black line extended from it represents the 95% confidence intervals, and the white dot is the median. 65

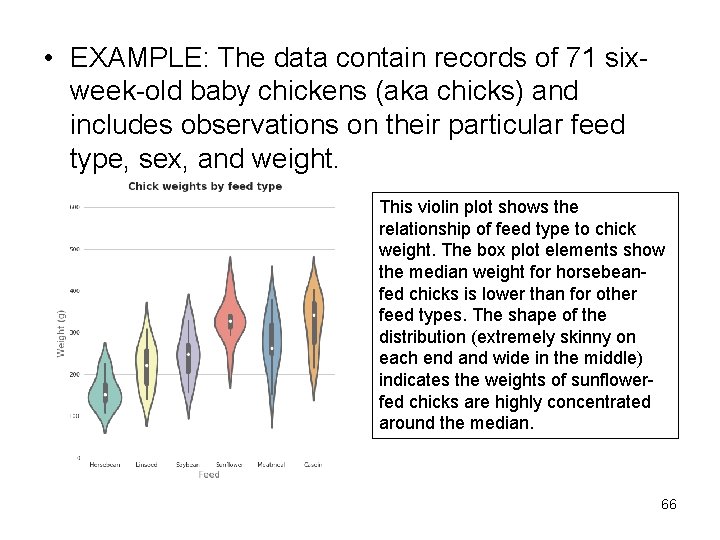
• EXAMPLE: The data contain records of 71 six week-old baby chickens (aka chicks) and includes observations on their particular feed type, sex, and weight. This violin plot shows the relationship of feed type to chick weight. The box plot elements show the median weight for horsebeanfed chicks is lower than for other feed types. The shape of the distribution (extremely skinny on each end and wide in the middle) indicates the weights of sunflowerfed chicks are highly concentrated around the median. 66

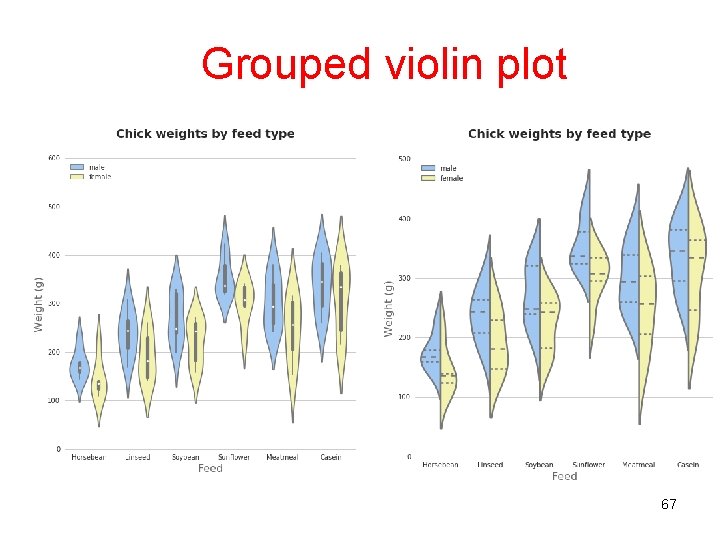
Grouped violin plot 67

VIOLIN PLOT IN R • Use ggplot 2 or vioplot. • Check the webpage http: //www. sthda. com/english/wiki/ggplot 2 -violinplot-quick-start-guide-r-software-and-datavisualization library(vioplot) plot(x, y, xlim=c(-5, 5), ylim=c(-2, 8)) vioplot(x, col=”gold”, horizontal=TRUE, at=-1, add=TRUE, lty=2, rect. Col=”gray”) vioplot(y, col=”blue”, horizontal=FALSE, at=-4, add=TRUE, lty=2) 68

KERNEL DENSITY ESTIMATION • A kernel is a special type of pdf with the added property that it must be even. Thus, a kernel is a function with the following properties • non-negative • real-valued • even • its definite integral over its support set must equal to 1 Some common pdfs are kernels; they include the Uniform(-1, 1) and standard normal distributions. 69

SOME KERNEL FUNCTIONS 70

What is Kernel Density Estimation? • Kernel density estimation is a non-parametric method of estimating the pdf of a continuous random variable. • It is non-parametric because it does not assume any underlying distribution for the variable. • Essentially, at every datum, a kernel function is created with the datum at its center – this ensures that the kernel is symmetric about the datum. The pdf is then estimated by adding all of these kernel functions and dividing by the number of data to ensure that it satisfies the 2 properties of a pdf. • Intuitively, a kernel density estimate is a sum of “bumps”. A “bump” is assigned to every datum, and the size of the “bump” represents the probability assigned at the neighborhood of values around that datum. 71

Constructing a Kernel Density Estimate: Step by Step 1. 2. Choose a kernel; the common ones are normal (Gaussian), uniform (rectangular), and triangular. At each datum xi, build the scaled kernel function where K() is the chosen kernel function, and h is the bandwidth (window width or smoothing parameter). 3. Add all of the individual scaled kernel functions and divide by n this places a probability 1/n of each xi. It also ensures that the kernel density estimate integrates to 1 over its support set. The density() function in R computes the values of the kernel density estimate. Applying the plot() function to an object created by density() will plot the estimate. Applying the summary() function to the object will reveal useful statistics about the estimate 72

Choosing the Bandwidth • The optimal bandwidth for a kernel density estimate is typically calculated on the basis of an estimate for the integrated squared error or the mean integrated squared error Both criteria should be minimized to obtain a good approximation of the unknown density. • Bandwidth describes how fast the weights fall off. If you're just using flat bins, you can just think of this as choosing how wide the bins are. In practice, it turns out that bandwidth is actually a lot more important than kernel shape. 73

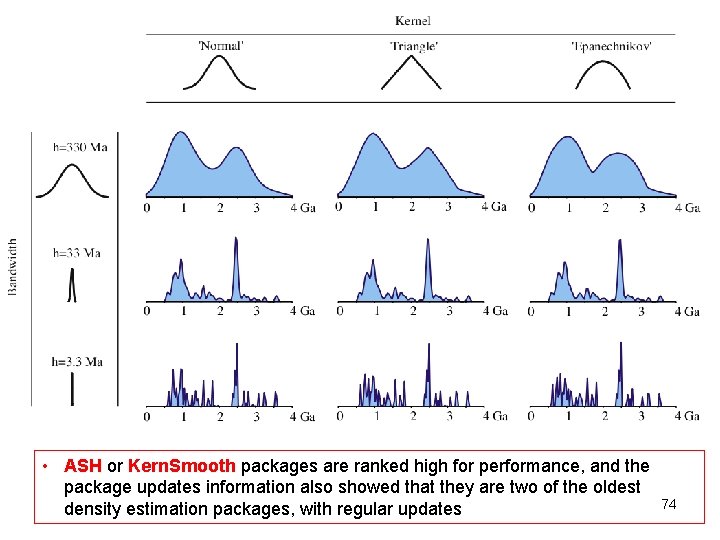
• ASH or Kern. Smooth packages are ranked high for performance, and the package updates information also showed that they are two of the oldest density estimation packages, with regular updates 74

Paired Data Sets and the Sample Correlation Coefficient • The covariance and the coefficient of correlation are used to measure the direction and strength of the linear relationship between two variables. – Covariance - is there any pattern to the way two variables move together? – Coefficient of correlation - how strong is the linear relationship between two variables 75

Covariance mx (my) is the population mean of the variable X (Y). N is the population size. x (y) is the sample mean of the variable X (Y). n is the sample size. 76

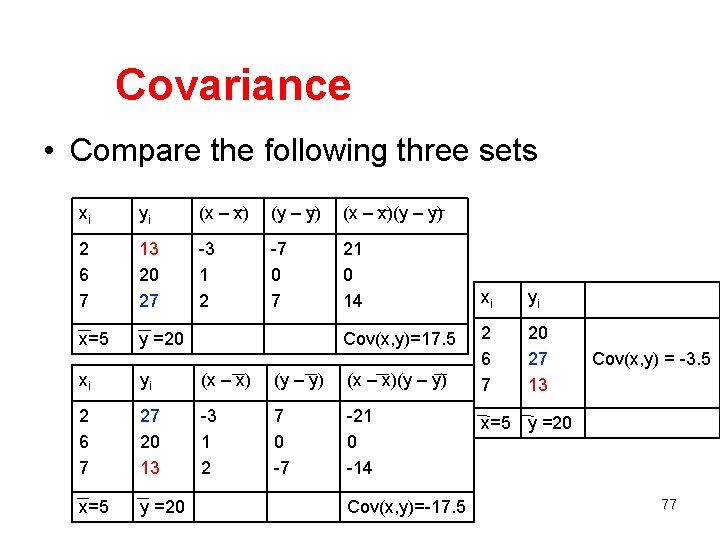
Covariance • Compare the following three sets xi yi (x – x) (y – y) (x – x)(y – y) 2 6 7 13 20 27 -3 1 2 -7 0 7 21 0 14 x=5 y =20 xi yi (x – x) (y – y) (x – x)(y – y) 2 6 7 27 20 13 -3 1 2 7 0 -7 -21 0 -14 x=5 y =20 Cov(x, y)=17. 5 Cov(x, y)=-17. 5 xi yi 2 6 7 20 27 13 Cov(x, y) = -3. 5 x=5 y =20 77

Covariance • If the two variables move in the same direction, (both increase or both decrease), the covariance is a large positive number. • If the two variables move in opposite directions, (one increases when the other one decreases), the covariance is a large negative number. • If the two variables are unrelated, the covariance will be close to zero. 78

The coefficient of correlation – This coefficient answers the question: How strong is the association between X and Y. 79

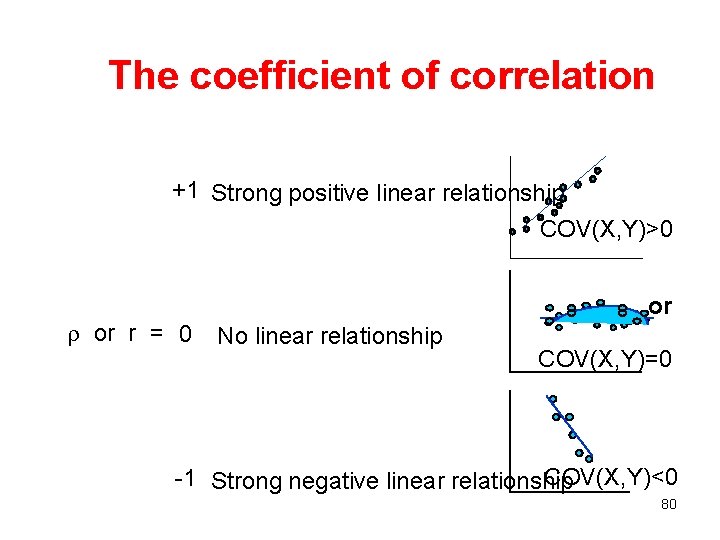
The coefficient of correlation +1 Strong positive linear relationship COV(X, Y)>0 r or r = 0 or No linear relationship COV(X, Y)=0 COV(X, Y)<0 -1 Strong negative linear relationship 80

The coefficient of correlation • If the two variables are very strongly positively related, the coefficient value is close to +1 (strong positive linear relationship). • If the two variables are very strongly negatively related, the coefficient value is close to -1 (strong negative linear relationship). • No straight line relationship is indicated by a coefficient close to zero. 81