Descriptive Statistics Numerical Methods Part 1 Measures of

Descriptive Statistics: Numerical Methods, Part 1 Measures of Location üThe Mean üThe Median üThe Mode üPercentiles üQuartiles

Mean The mean (or average) is the basic measure of location or “central tendency” of the data. • The sample mean sample statistic. is a • The population mean is a population statistic.

Sample Mean Where the numerator is the sum of values of n observations, or: The Greek letter Σ is the summation sign

Example: College Class Size We have the following sample of data for 5 college classes: 46 54 42 46 32 We use the notation x 1, x 2, x 3, x 4, and x 5 to represent the number of students in each of the 5 classes: X 1 = 46 x 2 = 54 x 3 = 42 x 4 = 46 x 5 = 32 Thus we have: The average class size is 44 students

Population Mean ( ) The number of observations in the population is denoted by the upper case N. The sample mean is a point estimator of the population mean

Median The median is the value in the middle when the data are arranged in ascending order (from smallest value to largest value). a. For an odd number of observations the median is the middle value. b. For an even number of observations the median is the average of the two middle values.

The College Class Size example First, arrange the data in ascending order: 32 42 46 46 54 Notice than n = 5, an odd number. Thus the median is given by the middle value. 32 42 46 46 54 The median class size is 46

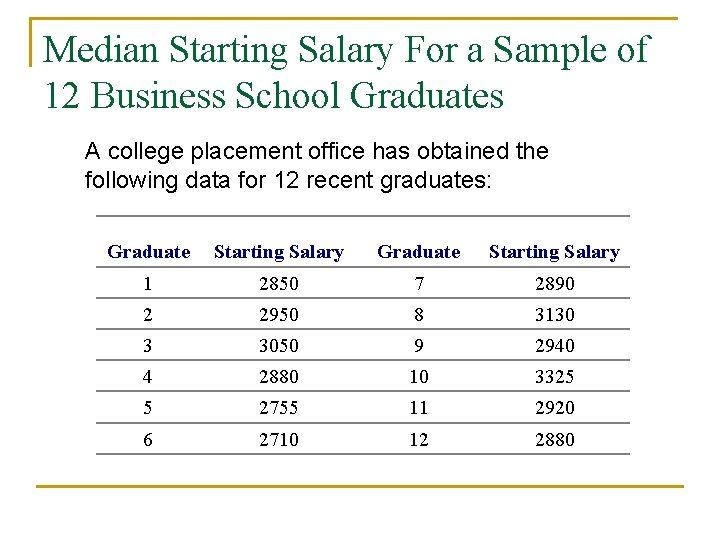
Median Starting Salary For a Sample of 12 Business School Graduates A college placement office has obtained the following data for 12 recent graduates: Graduate Starting Salary 1 2850 7 2890 2 2950 8 3130 3 3050 9 2940 4 2880 10 3325 5 2755 11 2920 6 2710 12 2880

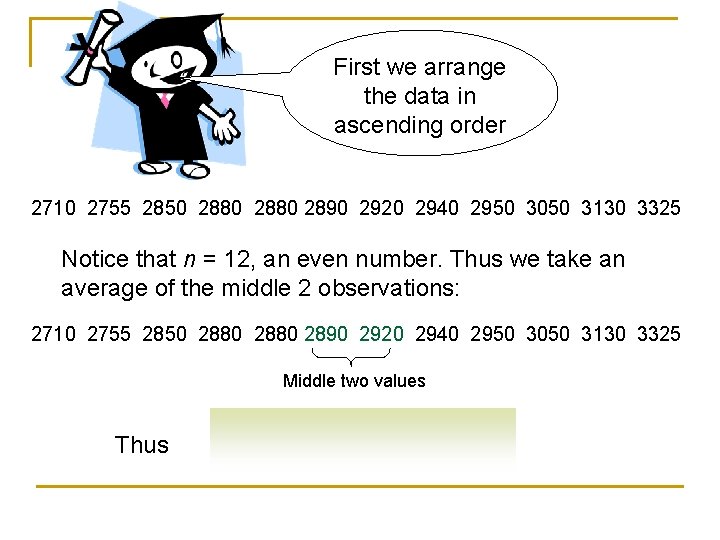
First we arrange the data in ascending order 2710 2755 2850 2880 2890 2920 2940 2950 3050 3130 3325 Notice that n = 12, an even number. Thus we take an average of the middle 2 observations: 2710 2755 2850 2880 2890 2920 2940 2950 3050 3130 3325 Middle two values Thus

Mode The mode is the value that occurs with greatest frequency Soft Drink Example Soft Drink Frequency Coke Classic 19 Diet Coke 8 Dr. Pepper 5 Pepsi Cola 13 Sprite 5 Total 50 The mode is Coke Classic. A mean or median is meaningless of qualitative data

Using Excel to Compute the Mean, Median, and Mode Enter the data into cells A 1: B 13 for the starting salary example. • To compute the mean, activate an empty cell and enter the following in the formula bar: =Average(b 2: b 13) and click the green checkmark. • To compute the median, activate an empty cell and enter the following in the formula bar: = Median(b 2: b 13) and click the green checkmark. • To compute the mode, activate an empty cell and enter the following in the formula bar: =Average(b 2: b 13) and click the green checkmark.

The Starting Salary Example Mean 2940 Median Mode 2905 2880

Percentiles The pth percentile is a value such that at least p percent of the observations are less than or equal to this value and at least (100 – p) percent of the observations are greater than or equal to this value. I scored in the 70 th percentile on the Graduate Record Exam (GRE)—meaning I scored higher than 70 percent of those who took the exam

Calculating the pth Percentile • Step 1: Arrange the data in ascendingorder (smallest value to largest value). • Step 2: Compute an index i where p is the percentile of interest and n in the number of observations. • Step 3: (a) If i is not an integer, round up. The next integer greater than i denotes the position of the pth percentile. (b) If i is an integer, the pth percentile is the average of values in i and i + 1

Example: Starting Salaries of Business Grads Let’s compute the 85 th percentile using the starting salary data. First arrange the data in ascending order. Step 1: 2710 2755 2850 2880 2890 2920 2940 2950 3050 3130 3325 Step 2: Step 3: Since 10. 2 in not an integer, round up to 11. The 85 thpercentile is the 11 th position (3130)

Quartiles are just specific percentiles Let: Q 1 = first quartile, or 25 th percentile Q 2 = second quartile, or 50 th percentile (also the median) Q 3 = third quartile, or 75 th percentile Let’s compute the 1 st and 3 rd percentiles using the starting salary data. Note we already computed the median for this sample—so we know the 2 nd quartile

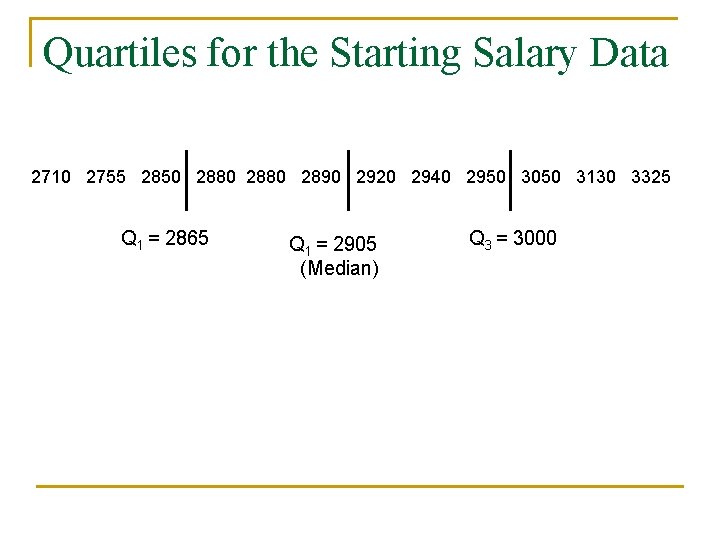
2710 2755 2850 2880 2890 2920 2940 2950 3050 3130 3325 Now find the 25 th percentile: Note that 3 is an integer, so to find the 25 th percentile we must average together the 3 rd and 4 th values: Q 1 = (2850 + 2880)/2 = 2865 Now find the 75 th percentile: Note that 9 is an integer, so to find the 75 th percentile we must average together the 9 th and 10 th values: Q 1 = (2950 + 3050)/2 = 3000

Quartiles for the Starting Salary Data 2710 2755 2850 2880 2890 2920 2940 2950 3050 3130 3325 Q 1 = 2865 Q 1 = 2905 (Median) Q 3 = 3000

Using Excel to Compute Percentiles and Quartiles Enter Data: Labels and starting salary data are entered into cells A 1: B 13 • Step 1: Activate any cell containing data in column B. • Step 2: Select the Data menu • Step 3; When the Sort dialog box appears: Sort by box, make sure that Starting Salary appears andthat Ascending is selected> Click OK