Measures of Location INFERENTIAL STATISTICS DESCRIPTIVE STATISTICS Statistics








- Slides: 16

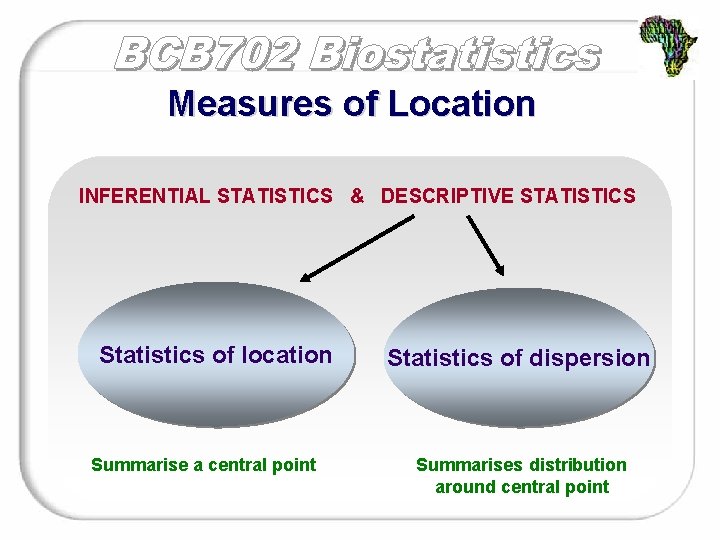
Measures of Location INFERENTIAL STATISTICS & DESCRIPTIVE STATISTICS Statistics of location Summarise a central point Statistics of dispersion Summarises distribution around central point

Measures of Location ARITHMETIC MEAN Sum all observation, then divide by number of observations For a sample: For a population:

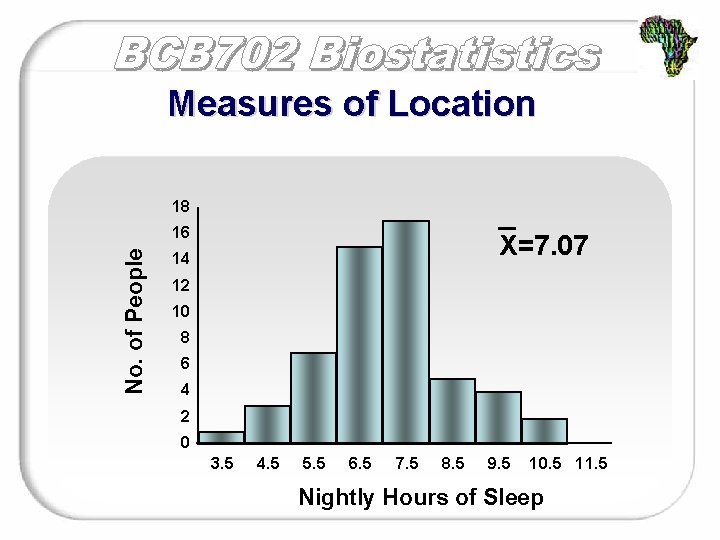
Measures of Location 18 No. of People 16 X=7. 07 14 12 10 8 6 4 2 0 3. 5 4. 5 5. 5 6. 5 7. 5 8. 5 9. 5 10. 5 11. 5 Nightly Hours of Sleep

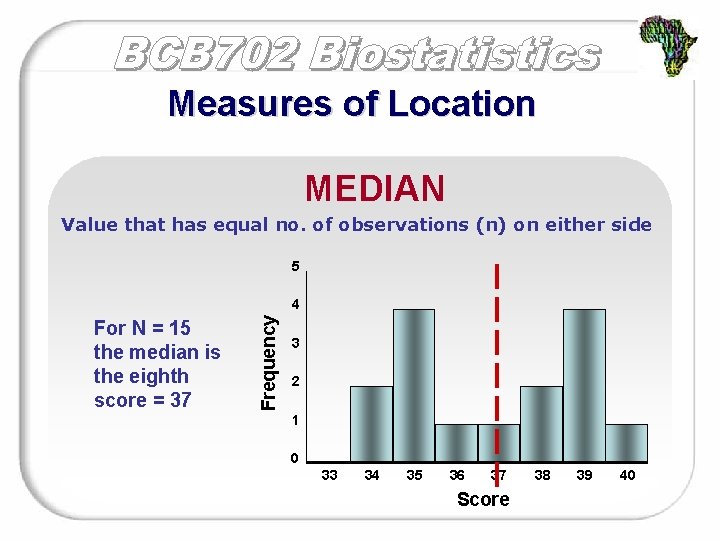
Measures of Location MEDIAN Value that has equal no. of observations (n) on either side 5 For N = 15 the median is the eighth score = 37 Frequency 4 3 2 1 0 33 34 35 36 37 Score 38 39 40

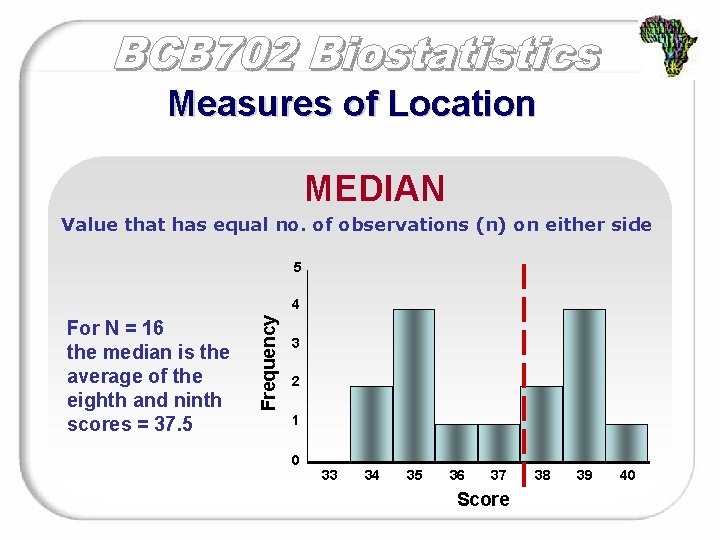
Measures of Location MEDIAN Value that has equal no. of observations (n) on either side 5 For N = 16 the median is the average of the eighth and ninth scores = 37. 5 Frequency 4 3 2 1 0 33 34 35 36 37 Score 38 39 40

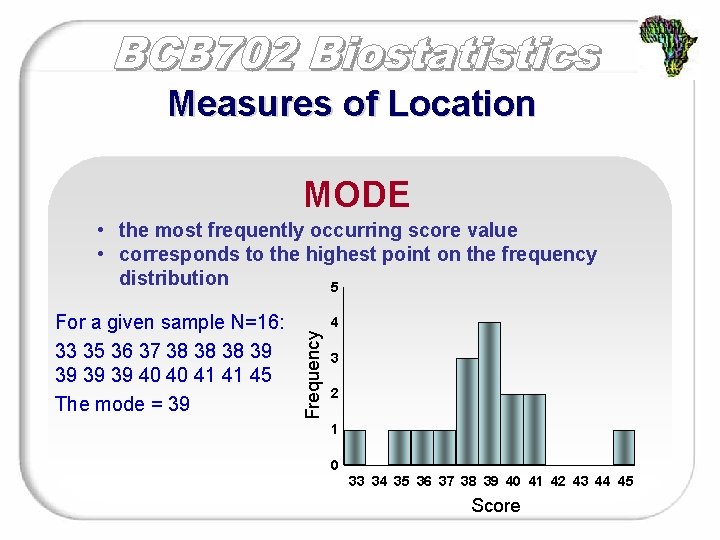
Measures of Location MODE • the most frequently occurring score value • corresponds to the highest point on the frequency distribution 5 4 Frequency For a given sample N=16: 33 35 36 37 38 38 38 39 39 40 40 41 41 45 The mode = 39 3 2 1 0 33 34 35 36 37 38 39 40 41 42 43 44 45 Score

Measures of Location Measures of central tendency Summary Advantages Mode quick & easy to compute l useful for nominal data l l Median sampling stability l related to variance l Mean not affected by extreme scores Disadvantages l poor sampling stability l somewhat poor sampling stability inappropriate for discrete data l affected by skewed distributions l

Measures of Location DISPERSION These are measures of how the observations are distributed around the mean

Measures of Location DISPERSION: Range

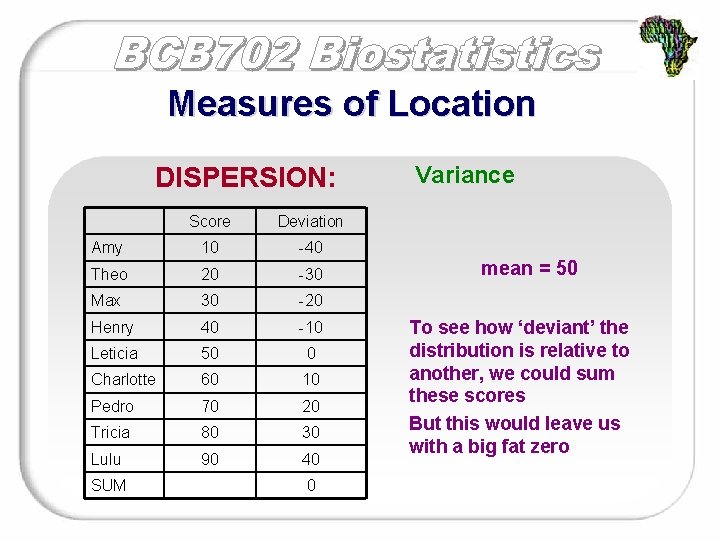
Measures of Location DISPERSION: Score Deviation Amy 10 -40 Theo 20 -30 Max 30 -20 Henry 40 -10 Leticia 50 0 Charlotte 60 10 Pedro 70 20 Tricia 80 30 Lulu 90 40 SUM 0 Variance mean = 50 To see how ‘deviant’ the distribution is relative to another, we could sum these scores But this would leave us with a big fat zero

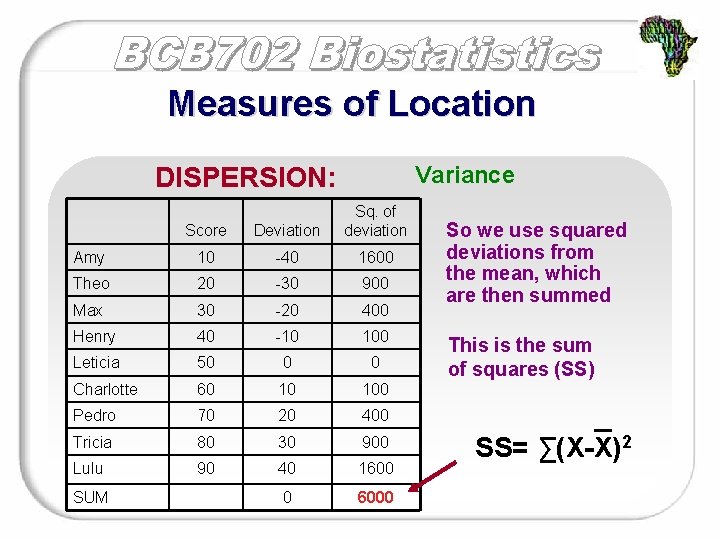
Measures of Location Variance DISPERSION: Score Deviation Sq. of deviation Amy 10 -40 1600 Theo 20 -30 900 Max 30 -20 400 Henry 40 -10 100 Leticia 50 0 0 Charlotte 60 10 100 Pedro 70 20 400 Tricia 80 30 900 Lulu 90 40 1600 0 6000 SUM So we use squared deviations from the mean, which are then summed This is the sum of squares (SS) SS= ∑(X-X)2

Measures of Location DISPERSION: Variance For a sample: (to correct for the fact that sample variance tends to underestimate pop variance) For a population: We take the “average” squared deviation from the mean and call it VARIANCE

Measures of Location DISPERSION: Standard deviation The standard deviation is the square root of the variance The standard deviation measures spread in the original units of measurement, while the variance does so in units squared. Variance is good for inferential stats. Standard deviation is nice for descriptive stats.

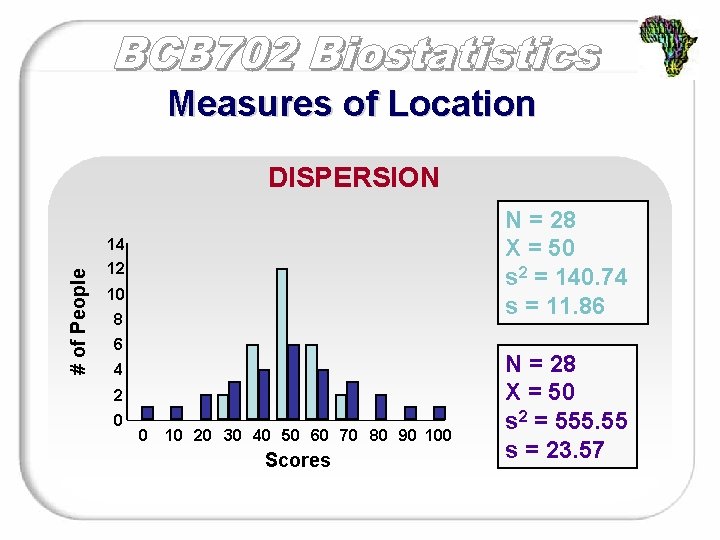
Measures of Location DISPERSION N = 28 X = 50 s 2 = 140. 74 s = 11. 86 # of People 14 12 10 8 6 4 2 0 0 10 20 30 40 50 60 70 80 90 100 Scores N = 28 X = 50 s 2 = 555. 55 s = 23. 57

Measures of Location DISPERSION For a sample: Mean Variance Standard Deviation For a population:

Measures of Location DISPERSION The Standard Error, or Standard Error of the Mean, is an estimate of the standard deviation of the sampling distribution of means, based on the data from one or more random samples e. g. 15 students each compile data sets of the heights of 20 people Numerically, it is equal to the square root of the quantity obtained when s squared is divided by the size of the sample. s = s X n and