Measures of Central Tendency MODE Grouped Data Prepared

































![Mo = 8. 5 + {[14 – 12] / [2(14) – 12 -10]}4 = Mo = 8. 5 + {[14 – 12] / [2(14) – 12 -10]}4 =](https://slidetodoc.com/presentation_image_h/9e094a0530ee4e98ee4215b314e0d742/image-38.jpg)

![Mo = 63. 5 + {[10 – 8] / [2(10) – 8 - 9]}3 Mo = 63. 5 + {[10 – 8] / [2(10) – 8 - 9]}3](https://slidetodoc.com/presentation_image_h/9e094a0530ee4e98ee4215b314e0d742/image-40.jpg)

![Mo = 6. 5 + {[8 – 4] / [2(8) – 4 - 5]}3 Mo = 6. 5 + {[8 – 4] / [2(8) – 4 - 5]}3](https://slidetodoc.com/presentation_image_h/9e094a0530ee4e98ee4215b314e0d742/image-42.jpg)



- Slides: 45

Measures of Central Tendency MODE (Grouped Data) Prepared by: Ryan L. Race Jenelyn A. Samsaman Rafaela M. Sarmiento Jorge O. Dela Cruz Maria Theresa S. Parajas Luning B. Federizo

Purpose/Rationale of this Module This module is designed to provide students with a step by step discussion on the computation of the mode for grouped data. It is to let the students discover for themselves how to compute for the mode (grouped data) through an easy visual presentation of the subject. Enjoy!

What Will You Learn From This Module? After studying this module, you should be able to: 1. Compute the mode for grouped data. 2. Use mode for grouped data to analyze and interpret data to solve problems in daily life.

Let’s See What You Already Know l Before you start studying this module, take the following test first to find out how prepared you are to solve for the mode of grouped data.

Find the mode of each of the following sets of numbers. a. 2, 4, 5, 1, 4, 6 Answer b. 77, 80, 90, 65, 77, 89, 80 Answer c. 1299, 2580, 4098, 9100, 1100 Answer

Answer: 4 Click me to answer letter b.

Answer: 77 and 80 Click me to answer letter c.

Answer: No Mode Go Back CONTINUE

For the next set of questions, refer to the given frequency distribution table of the grades of a group of students. CONTINUE

1. What is the modal class? Grades 90 – 94 Number of students 2 85 – 89 5 80 – 84 8 75 – 79 12 70 – 74 3 ANSWER

ANSWER: 75 – 79 The modal class is the class with the highest frequency. CONTINUE

2. What is the lower class boundary of the modal class? Grades 90 – 94 Number of students 2 85 – 89 5 80 – 84 8 (Modal Class) 75 – 79 70 – 74 ANSWER 12 3

ANSWER: Lmo = 74. 5 CONTINUE

3. What is the frequency of the modal class? Grades 90 – 94 85 – 89 80 – 84 (Modal Class) 75 – 79 70 – 74 Number of students 2 5 8 12 3 ANSWER

ANSWER: fmo = 12 CONTINUE

4. What is the frequency of the class preceding the modal class? Grades 90 – 94 85 – 89 80 – 84 (Modal Class) 75 – 79 70 – 74 Number of students 2 5 8 12 3 ANSWER

ANSWER: f 1 = 8 CONTINUE

5. What is the frequency of the class after the modal class? Grades 90 – 94 85 – 89 80 – 84 (Modal Class) 75 – 79 70 – 74 Number of students 2 5 8 12 3 ANSWER

ANSWER: f 2 = 3 CONTINUE

6. What is the class size? Grades 90 – 94 85 – 89 80 – 84 75 – 79 70 – 74 Number of students 2 5 8 12 3 ANSWER

ANSWER: i = 5 CONTINUE

Observe how the modal grade of the students is computed. Mode (Mo) = 74. 5 +{[( 12 – = 74. 5 + (4/13)5 8 )]/[2( 12 )– = 74. 5 + (20/13) = 76. 04 CONTINUE 8 – 3 ]} 5

74. 5 is the lower class boundary of the modal class (Lmo)

12 is the frequency of the modal class (fmo)

8 is the frequency of the class preceding the modal class (f 1)

3 is the frequency of the class after the modal class (f 2).

5 is the class size (i).

How did we solve for the modal grade of the students? Can you give the formula for the mode of grouped data? CONTINUE

To solve for the mode of grouped data, use the formula Mo = Lmo+{( fmo – f 1 )/( 2 fmo – f 1 – f 2 )}i where, Lmo is the lower class boundary of the modal class, fmo is the frequency of the modal class, f 1 is the frequency of the class preceding the modal class, f 2 is the frequency of the class after the modal class, and i is the class size. CONTINUE

Let’s Practice! The following distribution gives the number of hours allotted by 50 students to do their assignments in a week. Find the modal hour. SOLUTION Hours 1 -4 Number of Students 9 5 -8 12 9 - 12 14 13 - 16 10 17 - 20 4

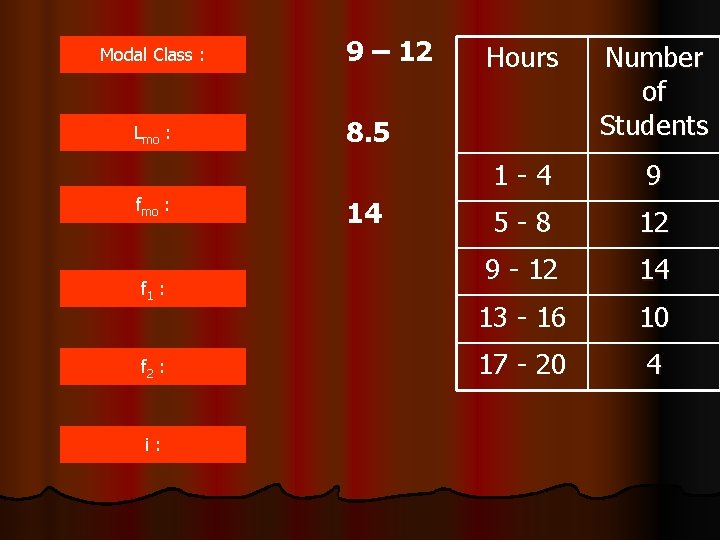
Modal Class : Lmo : f 1 : f 2 : i: Hours 1 -4 Number of Students 9 5 -8 12 9 - 12 14 13 - 16 10 17 - 20 4

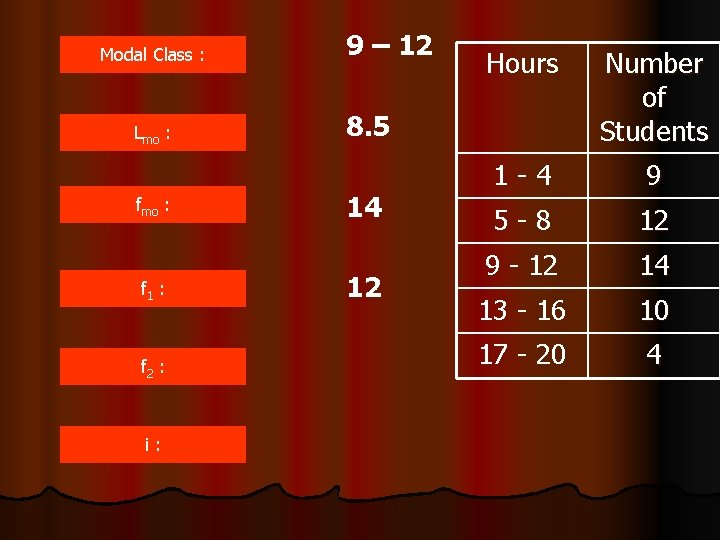
Modal Class : 9 – 12 Hours Number of Students 1 -4 9 5 -8 12 9 - 12 14 13 - 16 10 17 - 20 4 Lmo : f 1 : f 2 : i:

Modal Class : Lmo : f 1 : f 2 : i: 9 – 12 Hours Number of Students 1 -4 9 5 -8 12 9 - 12 14 13 - 16 10 17 - 20 4 8. 5

Modal Class : Lmo : f 1 : f 2 : i: 9 – 12 Hours Number of Students 1 -4 9 5 -8 12 9 - 12 14 13 - 16 10 17 - 20 4 8. 5 14

Modal Class : Lmo : f 1 : f 2 : i: 9 – 12 Hours Number of Students 1 -4 9 5 -8 12 9 - 12 14 13 - 16 10 17 - 20 4 8. 5 14 12

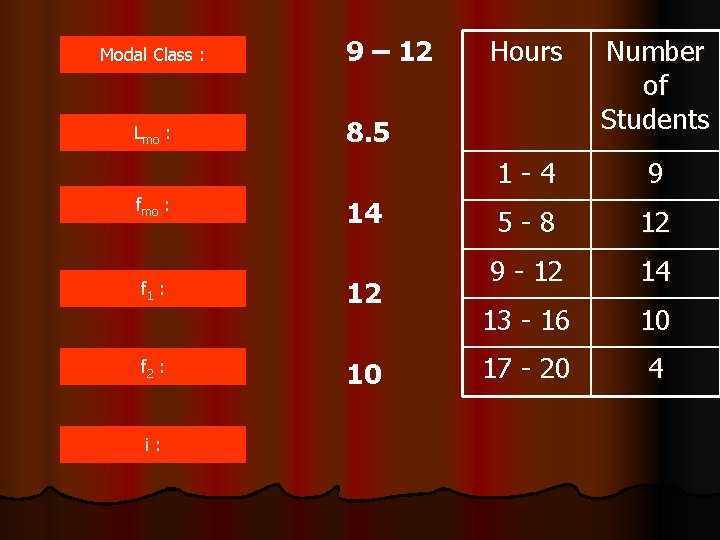
Modal Class : Lmo : fmo : 9 – 12 Number of Students 1 -4 9 5 -8 12 9 - 12 14 13 - 16 10 17 - 20 4 8. 5 14 f 1 : 12 f 2 : 10 i: Hours

Modal Class : 9 – 12 Lmo : 8. 5 fmo : 14 f 1 : 12 f 2 : 10 i: 4 Compute the mode
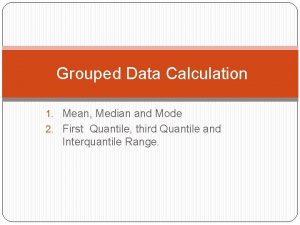
![Mo 8 5 14 12 214 12 104 Mo = 8. 5 + {[14 – 12] / [2(14) – 12 -10]}4 =](https://slidetodoc.com/presentation_image_h/9e094a0530ee4e98ee4215b314e0d742/image-38.jpg)
Mo = 8. 5 + {[14 – 12] / [2(14) – 12 -10]}4 = 8. 5 + (2/6)4 = 8. 5 + 1. 33 = 9. 83 CONTINUE

More Practice? Find the mode using the frequency distribution of the heights of 40 students. SOLUTION SKIP Height(inches) No. of Students 52 – 54 2 55 – 57 4 58 – 60 3 61 - 63 8 64 – 66 10 67 – 69 9 70 - 72 4
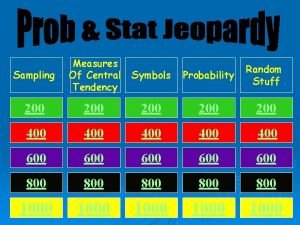
![Mo 63 5 10 8 210 8 93 Mo = 63. 5 + {[10 – 8] / [2(10) – 8 - 9]}3](https://slidetodoc.com/presentation_image_h/9e094a0530ee4e98ee4215b314e0d742/image-40.jpg)
Mo = 63. 5 + {[10 – 8] / [2(10) – 8 - 9]}3 = 63. 5 + (2/3)3 = 63. 5 + 2 = 65. 5 NEXT

EVALUATE YOURSELF Find the mode of 20 students whose scores on a 15 -point test are given in the following distribution: SOLUTION Scores 1– 3 No. of Students 1 4– 6 4 7– 9 8 10 – 12 5 13 - 15 2
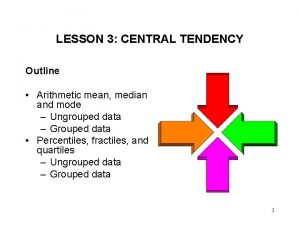
![Mo 6 5 8 4 28 4 53 Mo = 6. 5 + {[8 – 4] / [2(8) – 4 - 5]}3](https://slidetodoc.com/presentation_image_h/9e094a0530ee4e98ee4215b314e0d742/image-42.jpg)
Mo = 6. 5 + {[8 – 4] / [2(8) – 4 - 5]}3 = 6. 5 + (4/7)3 = 6. 5 + 1. 714 = 8. 21 NEXT

Try Another One A sample of 40 tourists traveled to Puerto Galera with the distribution based on the length of their stay (in years). Find the mode. SOLUTION Length of Stay (years) 1– 8 No. of Tourists 9 – 16 7 17 – 24 5 25 – 32 6 33 - 40 5 8


 Central tendency of grouped data
Central tendency of grouped data Mode of grouped data formula
Mode of grouped data formula Lower boundary of the modal class
Lower boundary of the modal class Central tendency symbols
Central tendency symbols Measures of central tendency
Measures of central tendency Objective of central tendency
Objective of central tendency Range in central tendency
Range in central tendency Objectives of central tendency
Objectives of central tendency Measures of central tendency
Measures of central tendency Measures of central tendency
Measures of central tendency Advantages of measures of central tendency
Advantages of measures of central tendency Central tendency worksheet
Central tendency worksheet Central tendency symbols
Central tendency symbols Central tendency symbols
Central tendency symbols Measures of central tendency and variation
Measures of central tendency and variation Statistics chapter 3 measures of central tendency
Statistics chapter 3 measures of central tendency Mode in statistics
Mode in statistics Measures of central tendency symbols
Measures of central tendency symbols Measures of central tendency notes
Measures of central tendency notes In quartiles central tendency median is
In quartiles central tendency median is How to do percentile calculation
How to do percentile calculation What is a mode ultrasound
What is a mode ultrasound Variance for grouped data
Variance for grouped data Mid range formula
Mid range formula Central tendancy bias
Central tendancy bias Central tendency and spread homework
Central tendency and spread homework Use of central tendency
Use of central tendency Central tendency
Central tendency How to calculate mode from mean and median
How to calculate mode from mean and median Contoh ukuran tendensi sentral
Contoh ukuran tendensi sentral Ukuran tendensi sentral
Ukuran tendensi sentral Fraktil adalah
Fraktil adalah Variance meaning
Variance meaning Importance of central tendency
Importance of central tendency Mean terkaan
Mean terkaan Central tendency symbols
Central tendency symbols Central tendencies statistics
Central tendencies statistics Objective of central tendency
Objective of central tendency Central tendency spss
Central tendency spss Summarion notation
Summarion notation Median even number
Median even number How to get frequency distribution
How to get frequency distribution Central tendency symbols
Central tendency symbols Repeated measures design
Repeated measures design Percentile formula for grouped data
Percentile formula for grouped data Variance formula for ungrouped data example
Variance formula for ungrouped data example