Measures of Central Tendency Section 2 3 Central


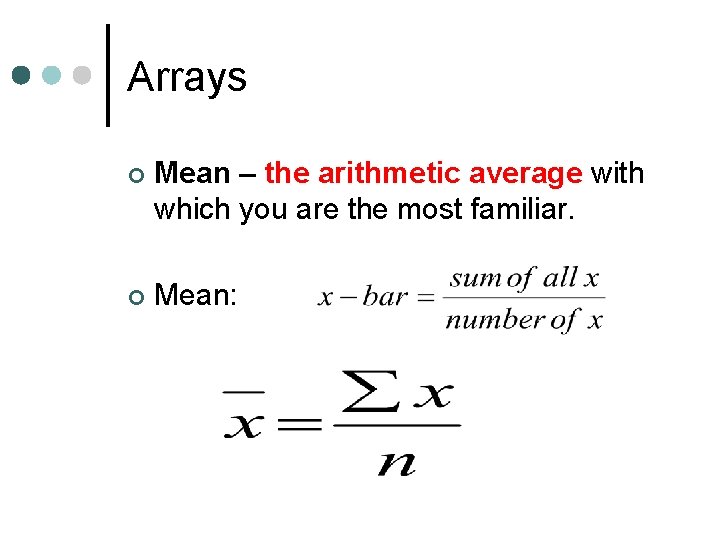


























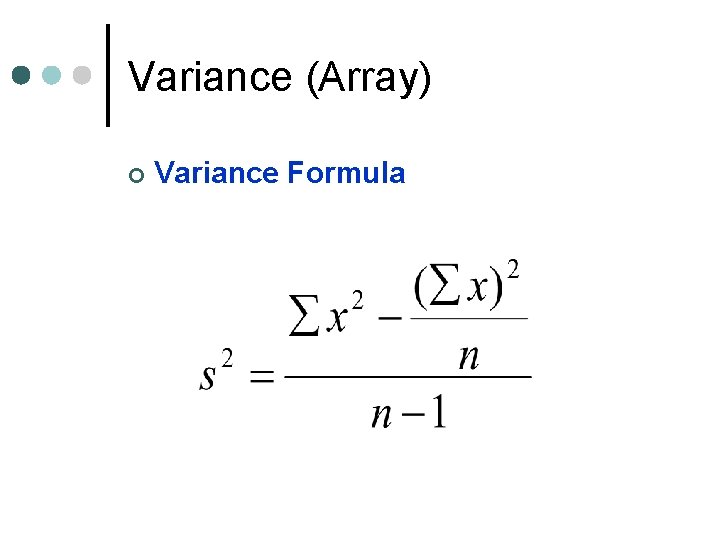







- Slides: 45

Measures of Central Tendency Section 2. 3

Central Values There are 4 values that are considered measures of the center. ¢ 1. Mean ¢ 2. Median ¢ 3. Mode ¢ 4. Midrange ¢
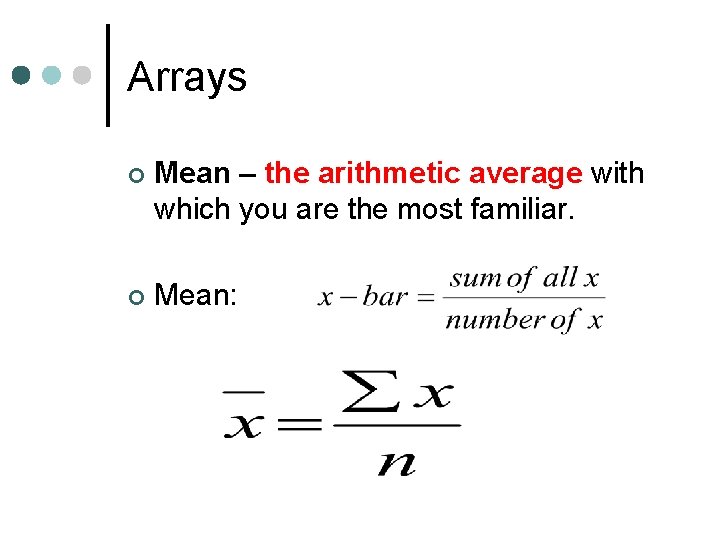
Arrays ¢ Mean – the arithmetic average with which you are the most familiar. ¢ Mean:

Sample and Population Symbols ¢ As we progress in this course there will be different symbols that represent the same thing. The only difference is that one comes from a sample and one comes from a population.

Symbols for Mean ¢ Sample Mean: ¢ Population Mean:

Rounding Rule ¢ Round answers to one decimal place more than the number of decimal places in the original data. ¢ Example: 2, 3, 4, 5, 6, 8 A Sample answer would be 4. 1

Example ¢ Find the mean of the array. ¢ 4, 3, 8, 9, 1, 7, 12

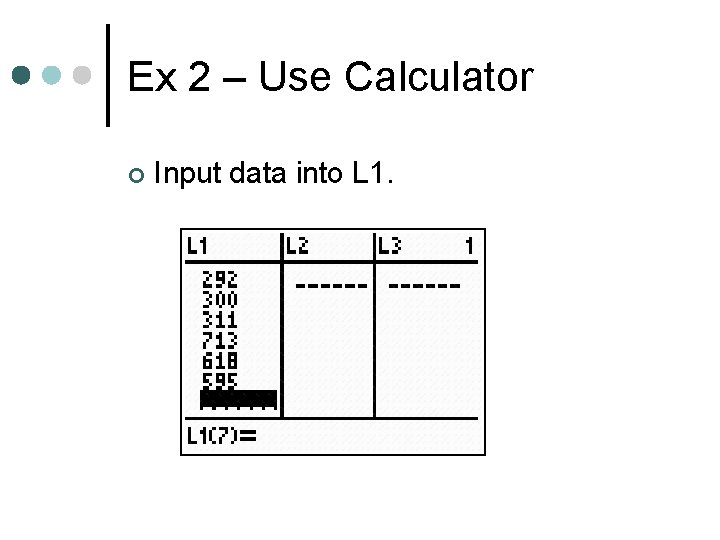
Example 2 – Use Calculator Find the mean of the array. 2. 0, 4. 9, 6. 5, 2. 1, 5. 1, 3. 2, 16. 6 Use your lists on the calculator and follow the steps.

Stat, Edit – input list

Stat, Calc, One-Var Stats, L 1

Or…. . (I like this way better!) ¢ ¢ ¢ 2 nd Stat Math 3: Mean (L#)

Rounding ¢ The mean (x-bar) is 5. 77. ¢ We used 2 decimal places because our original data had 1 decimal place.

Median – the middle number in an ordered set of numbers. Divides the data into two equal parts. ¢ Odd # in set: falls exactly on the middle number. ¢ Even # in set: falls in between the two middle values in the set; find the average of the two middle values. ¢

Example ¢ Find the median. ¢ A. 2, 3, 4, 7, 8 ¢ B. 6, 7, 8, 9, 9, 10 median = (8+9)/2 = 8. 5. - the median is 4.

Ex 2 – Use Calculator ¢ Input data into L 1.

Run “Stat, Calc, One-Variable Stats, L 1” ¢ Cursor all the way down to find “med” ¢

Or……. 2 nd ¢ Stat ¢ Math ¢ 4: Median(L#) ¢

Mode ¢ The number that occurs most often. ¢ Suggestion: Sort the numbers in L 1 to make it easier to see the grouping of the numbers. ¢ You can have a single number for the mode, no mode, or more than one number.

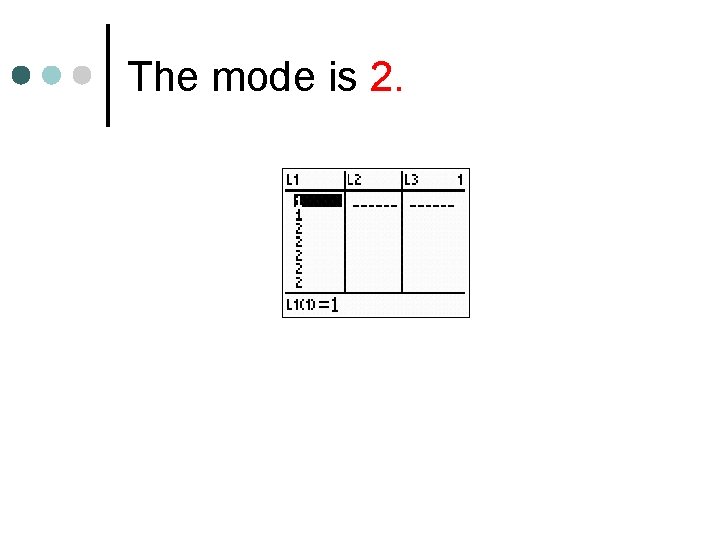
Example Find the mode. ¢ 1, 2, 2, 2, 1, 3, 3 ¢ Put numbers in L 1 and sort to see the groupings easier. ¢

The mode is 2.

Ex 2 ¢ Find the mode. ¢ A. 0, 1, 2, 3, 4 ¢ B. 4, 4, 6, 7, 8, 9, 6, 9 - 4 , 6, and 9 - no mode

Midrange ¢ The number exactly midway between the lowest value and highest value of the data set. It is found by averaging the low and high numbers.

Example ¢ Find the midrange of the set. ¢ 3, 3, 5, 6, 8

Measures of Dispersion…. . Arrays Section 2. 4

Dispersion ¢ The measure of the spread or variability ¢ No Variability – No Dispersion

Measures of Variation ¢ There are 3 values used to measure the amount of dispersion or variation. (The spread of the group) 1. Range 2. Variance 3. Standard Deviation

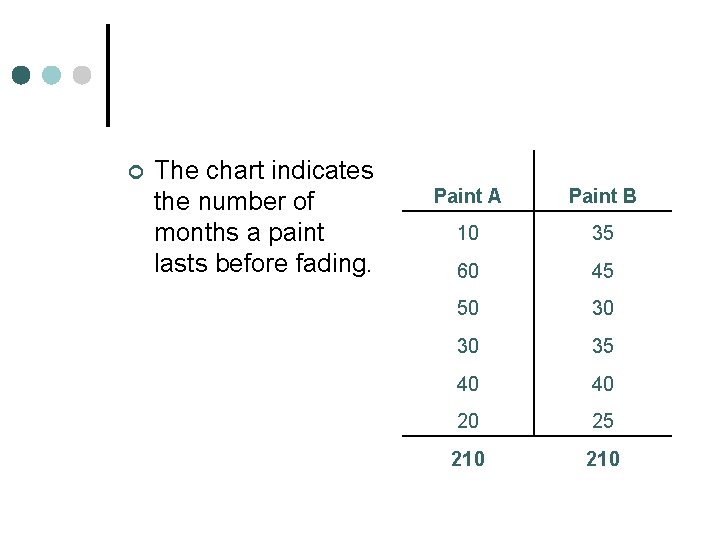
Why is it Important? ¢ You want to choose the best brand of paint for your house. You are interested in how long the paint lasts before it fades and you must repaint. The choices are narrowed down to 2 different paints. The results are shown below. Which paint would you choose?

¢ The chart indicates the number of months a paint lasts before fading. Paint A Paint B 10 35 60 45 50 30 30 35 40 40 20 25 210

Does the Average Help? ¢ Paint A: Avg = 210/6 = 35 months ¢ Paint B: Avg = 210/6 = 35 months ¢ They both last 35 months before fading. No help in deciding which to buy.

Consider the Spread ¢ Paint A: Spread = 60 – 10 = 50 months ¢ Paint B: Spread = 45 – 25 = 20 months ¢ Paint B has a smaller variance which means that it performs more consistently. Choose paint B.

Range ¢ The range is the difference between the lowest value in the set and the highest value in the set. ¢ Range = High # - Low #

Example ¢ Find the range of the data set. ¢ 40, 30, 15, 2, 100, 37, 24, 99 ¢ Range = 100 – 2 = 98

Deviation from the Mean ¢ A deviation from the mean, x – x bar, is the difference between the value of x and the mean x bar. We base our formulas for variance and standard deviation on the amount that they deviate from the mean. ¢ We’ll use a shortcut formula – not in book.
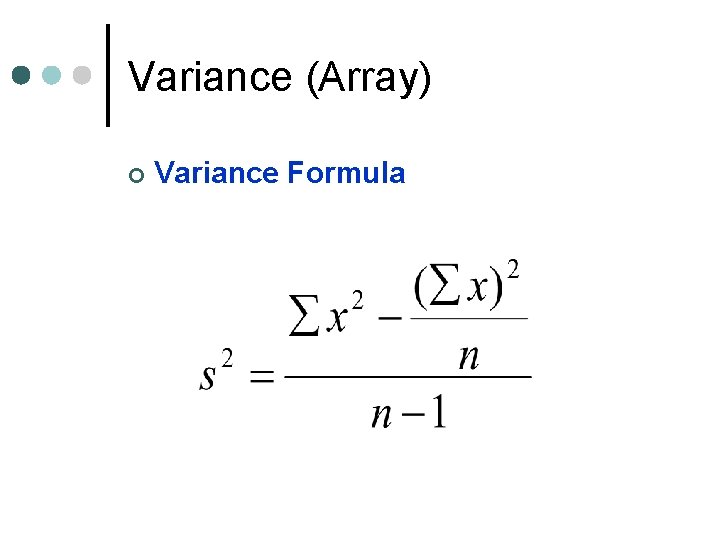
Variance (Array) ¢ Variance Formula

Standard Deviation ¢ The standard deviation is the square root of the variance.

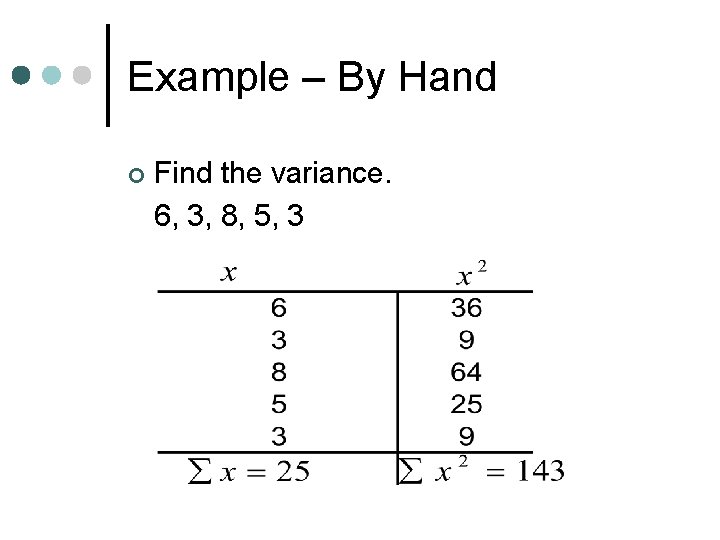
Example – By Hand ¢ Find the variance. 6, 3, 8, 5, 3


Find the standard deviation ¢ The standard deviation is the square root of the variance.

Same Example – Use Calculator ¢ Put numbers in L 1.

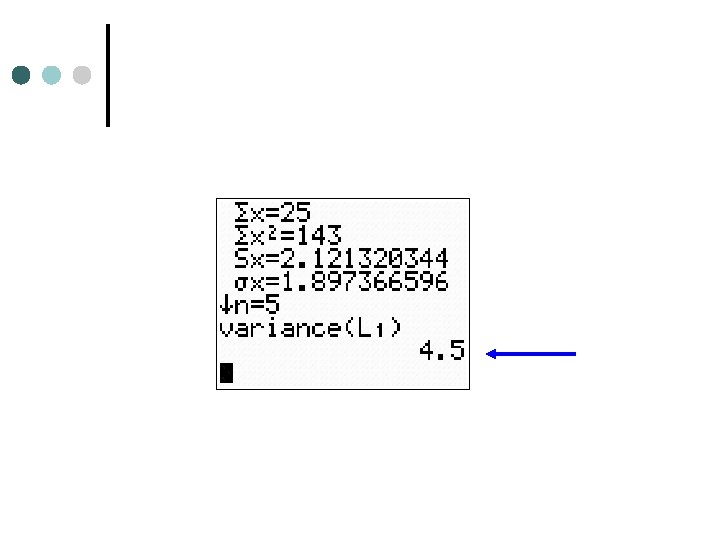
¢ Run “Stat, Calc, One-Variable Stats, L 1” and read the numbers. Remember you have to square the standard deviation to get variance.

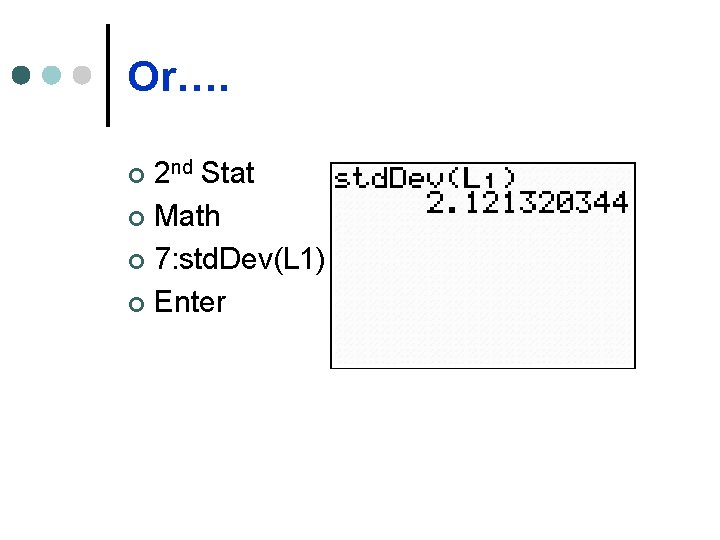
Or…. 2 nd Stat ¢ Math ¢ 7: std. Dev(L 1) ¢ Enter ¢

Variance – By Hand ¢ Square the ENTIRE number for the standard deviation not the rounded version you gave for your answer.

Variance on Calculator 2 nd Stat ¢ Math ¢ 8: Variance (L 1) ¢

