Sec 4 4 Composite Numerical Integration Sec 4








- Slides: 9

Sec: 4. 4 Composite Numerical Integration

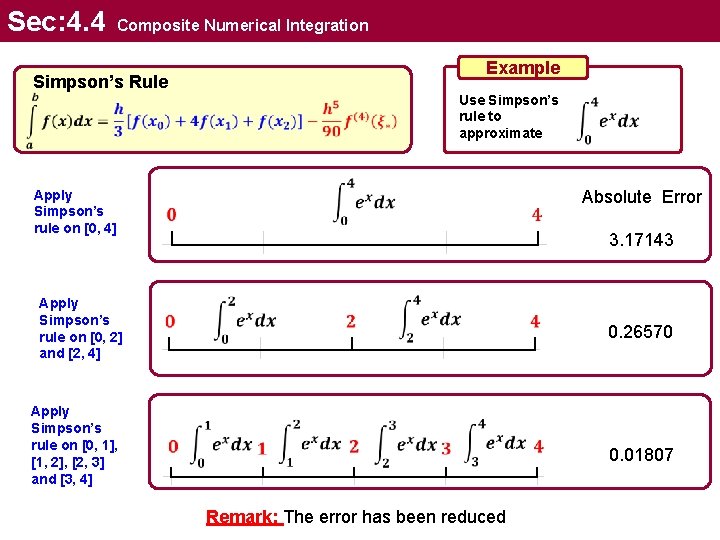
Sec: 4. 4 Composite Numerical Integration Example Simpson’s Rule Apply Simpson’s rule on [0, 4] Apply Simpson’s rule on [0, 2] and [2, 4] Apply Simpson’s rule on [0, 1], [1, 2], [2, 3] and [3, 4] Use Simpson’s rule to approximate Absolute Error 3. 17143 Remark: The error has been reduced 0. 26570 0. 01807

Sec: 4. 4 Composite Numerical Integration To generalize this procedure Simpson’s Rule 1) choose an even integer n 2) Subdivide the interval [a, b] into n subintervals 3) apply Simpson’s rule on each consecutive pair of subintervals

Sec: 4. 4 Composite Numerical Integration Extreme value theorem and Intermediate value theorem give Theorem Notice that the error term for the Composite Simpson’s rule is O(h 4), whereas it was O(h 5) for the standard Simpson’s rule. However, these rates are not comparable because of different values of h. Simpson’s Rule

Sec: 4. 4 Composite Numerical Integration The subdivision approach can be applied to any of the Newton. Cotes formulas. Such as the Trapezoidal and Midpoint rules The Trapezoidal rule requires only one interval for each application, so the integer n can be either odd or even. The Trapezoidal Rule Theorem The midpoint Rule

Sec: 4. 4 Composite Numerical Integration Composite Simpson’s rule Composite Trapezoidal rule Example (a) 360 (b) n=18 with 19 function evaluations 1+8+9+1 accurate to within about 1 e-5 (*) Composite Trapezoidal with n=18 requires 19 function evaluations 1+17+1 accurate only to about 5 e-3

Sec: 4. 4 Composite Numerical Integration Remarks: 1) The Newton-Cotes formulas are generally unsuitable for use over large integration intervals. High-degree formulas would be required 2) The values of the coefficients in these formulas are difficult to obtain. 3) The Newton-Cotes formulas are based on interpolatory polynomials that use equally-spaced nodes, a procedure that is inaccurate over large intervals because of the oscillatory nature of high-degree polynomials.

Sec: 4. 4 Composite Numerical Integration

Sec: 4. 4 Composite Numerical Integration