Gausss Law applications Chapter 24 Gausss Law The

Gauss’s Law: applications Chapter 24

Gauss’s Law The total flux within a closed surface … … is proportional to the enclosed charge. Gauss’s Law is always true, but is only useful for certain very simple problems with great symmetry.

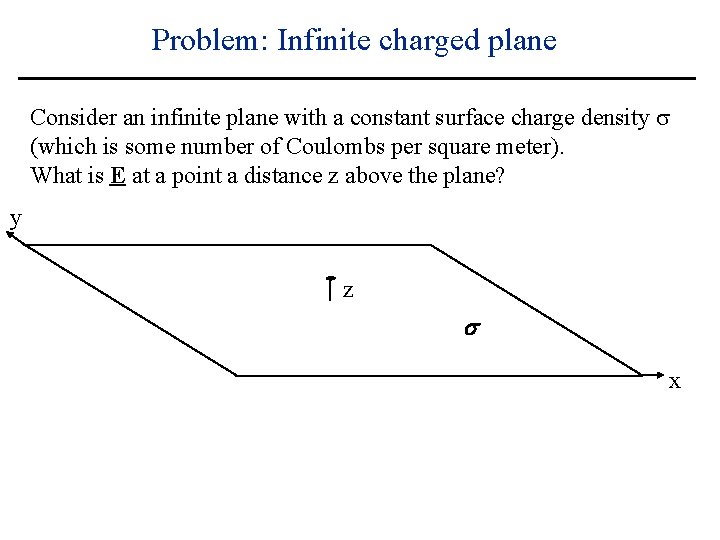
Problem: Infinite charged plane Consider an infinite plane with a constant surface charge density s (which is some number of Coulombs per square meter). What is E at a point a distance z above the plane? y z s x

Problem: Infinite charged plane Consider an infinite plane with a constant surface charge density s (which is some number of Coulombs per square meter). What is E at a point a distance z above the plane? y E z s x Step 1: Use symmetry

Problem: Infinite charged plane Consider an infinite plane with a constant surface charge density s (which is some number of Coulombs per square meter). What is E at a point a distance z above the plane? y E z s x Step 1: Use symmetry The electric field must point straight away from the plane (if s>0). Maybe the magnitude E depends on z, but the direction is fixed. And E is independent of x and y.

Problem: Infinite charged plane Consider an infinite plane with a constant surface charge density s (which is some number of Coulombs per square meter). What is E at a point a distance z above the plane? E y E z s E Step 1: Use symmetry x The electric field must point straight away from the plane (if s>0). Maybe the magnitude E depends on z, but the direction is fixed. And E is independent of x and y.

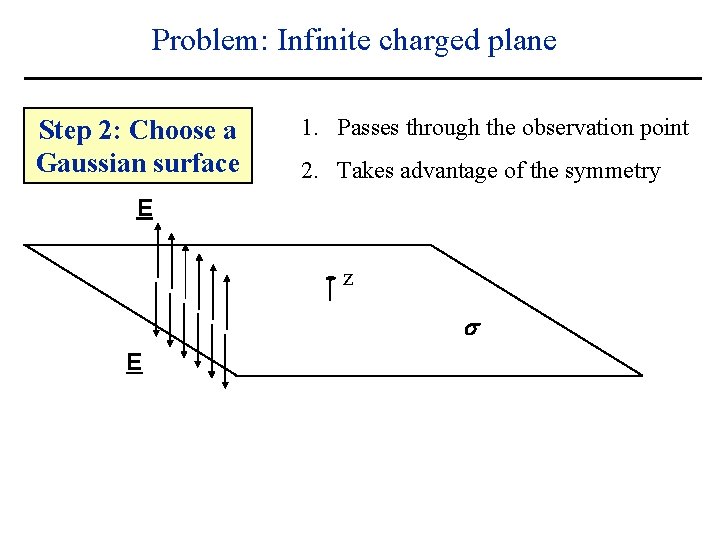
Problem: Infinite charged plane Step 2: Choose a Gaussian surface 1. Passes through the observation point 2. Takes advantage of the symmetry E z s E

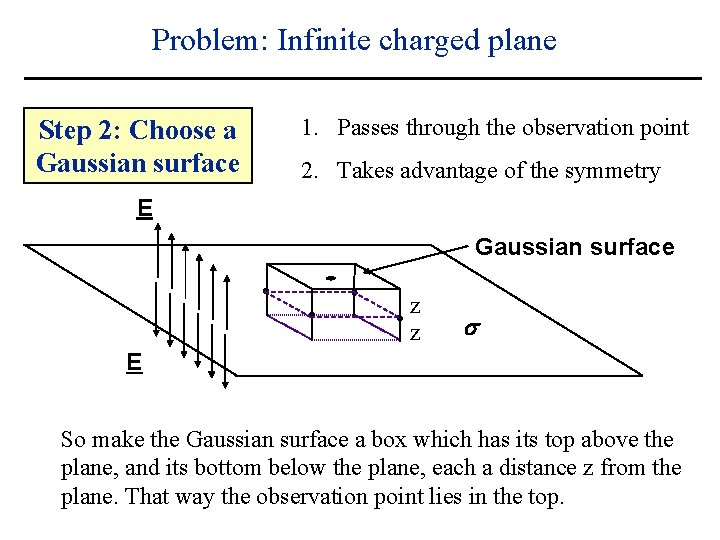
Problem: Infinite charged plane Step 2: Choose a Gaussian surface 1. Passes through the observation point 2. Takes advantage of the symmetry E Gaussian surface z z s E So make the Gaussian surface a box which has its top above the plane, and its bottom below the plane, each a distance z from the plane. That way the observation point lies in the top.

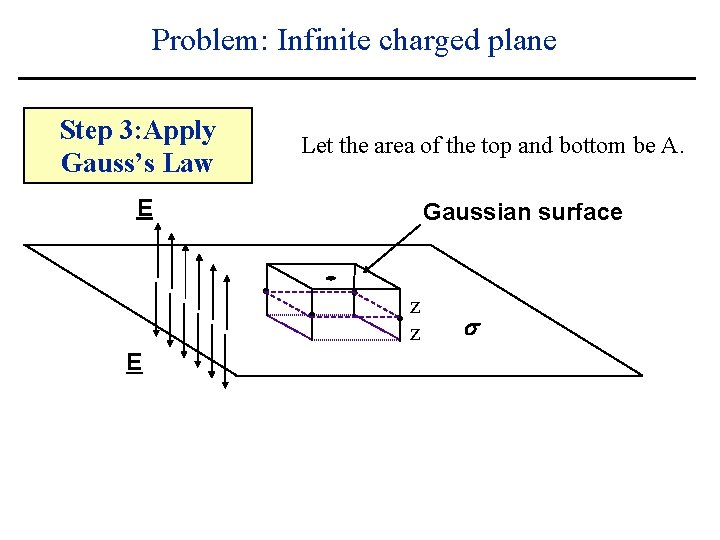
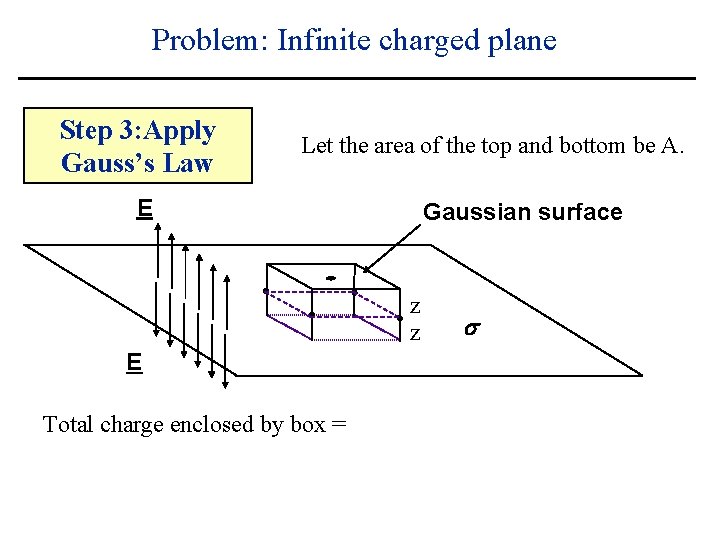
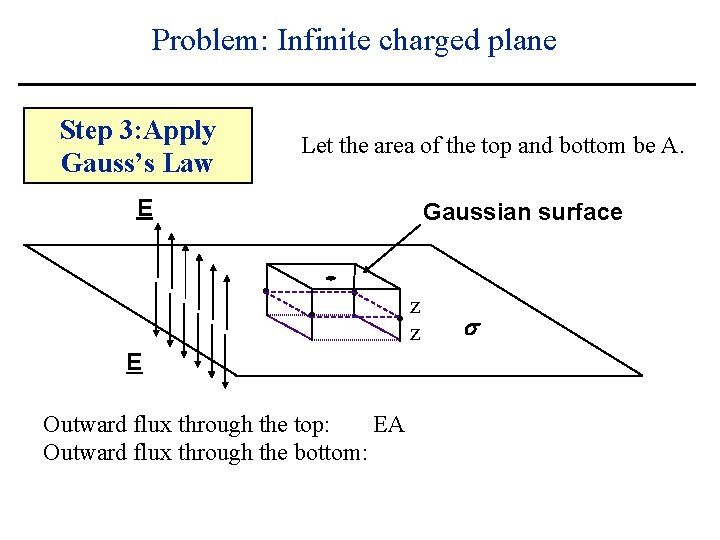
Problem: Infinite charged plane Step 3: Apply Gauss’s Law Let the area of the top and bottom be A. E Gaussian surface z z E s

Problem: Infinite charged plane Step 3: Apply Gauss’s Law Let the area of the top and bottom be A. E Gaussian surface z z E Total charge enclosed by box = s

Problem: Infinite charged plane Step 3: Apply Gauss’s Law Let the area of the top and bottom be A. E Gaussian surface z z E Total charge enclosed by box = As s

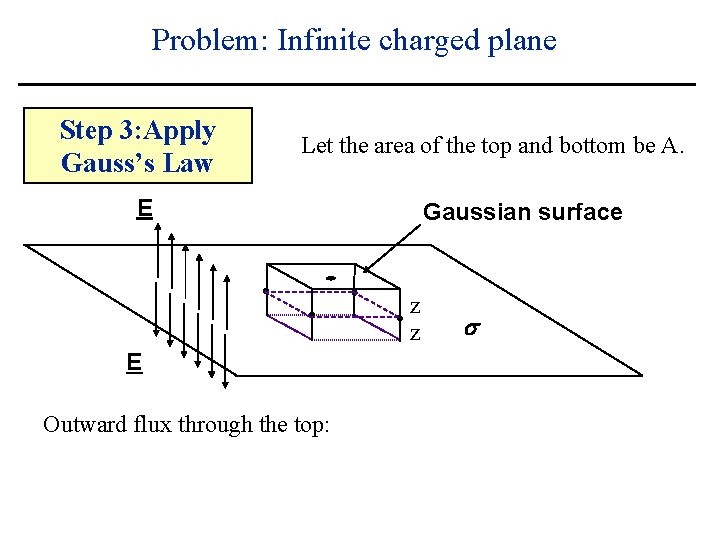
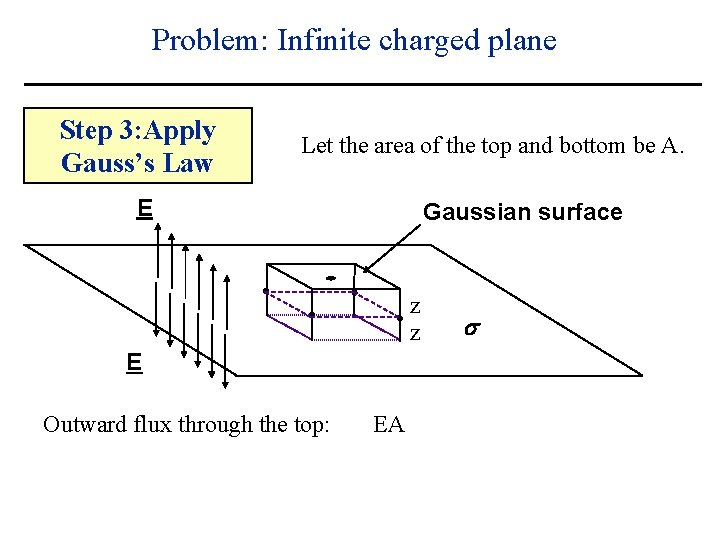
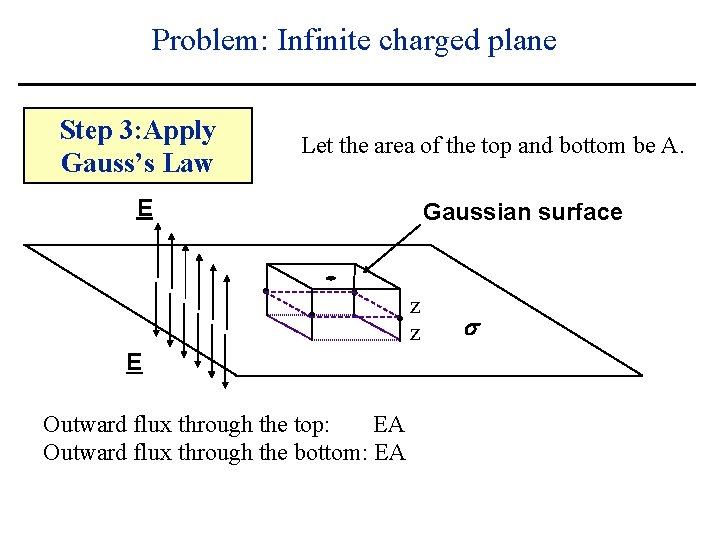
Problem: Infinite charged plane Step 3: Apply Gauss’s Law Let the area of the top and bottom be A. E Gaussian surface z z E Outward flux through the top: s

Problem: Infinite charged plane Step 3: Apply Gauss’s Law Let the area of the top and bottom be A. E Gaussian surface z z E Outward flux through the top: EA s

Problem: Infinite charged plane Step 3: Apply Gauss’s Law Let the area of the top and bottom be A. E Gaussian surface z z E Outward flux through the top: EA Outward flux through the bottom: s

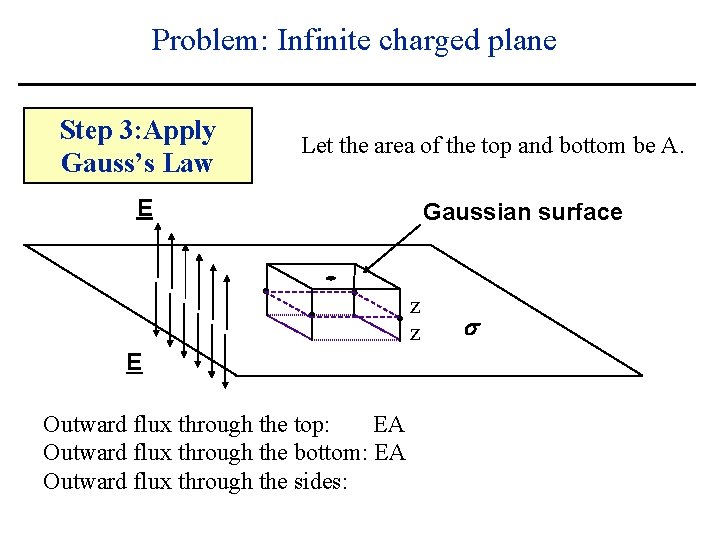
Problem: Infinite charged plane Step 3: Apply Gauss’s Law Let the area of the top and bottom be A. E Gaussian surface z z E Outward flux through the top: EA Outward flux through the bottom: EA s

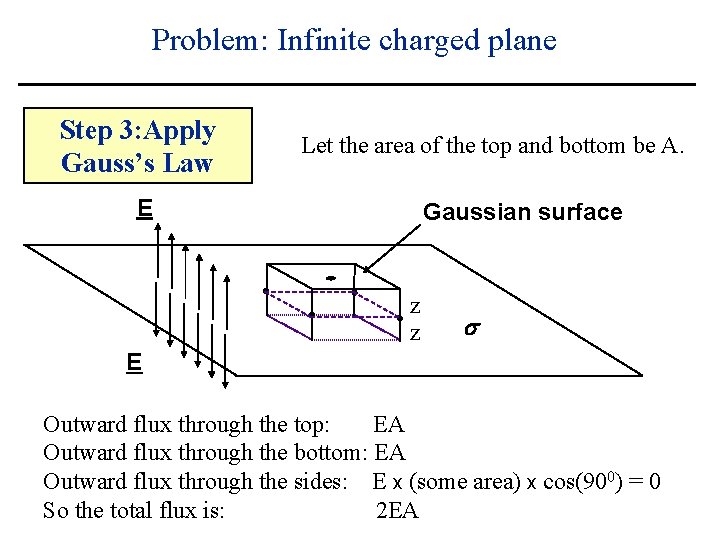
Problem: Infinite charged plane Step 3: Apply Gauss’s Law Let the area of the top and bottom be A. E Gaussian surface z z E Outward flux through the top: EA Outward flux through the bottom: EA Outward flux through the sides: s

Problem: Infinite charged plane Step 3: Apply Gauss’s Law Let the area of the top and bottom be A. E Gaussian surface z z s E Outward flux through the top: EA Outward flux through the bottom: EA Outward flux through the sides: E x (some area) x cos(900) = 0

Problem: Infinite charged plane Step 3: Apply Gauss’s Law Let the area of the top and bottom be A. E Gaussian surface z z s E Outward flux through the top: EA Outward flux through the bottom: EA Outward flux through the sides: E x (some area) x cos(900) = 0 So the total flux is: 2 EA

Problem: Infinite charged plane Step 3: Apply Gauss’s Law Let the area of the top and bottom be A. E Gaussian surface z z s E Gauss’s law then says that As/e 0=2 EA so that E=s/2 e 0, outward. This is constant everywhere in each half-space! Notice that the area A canceled: this is typical!

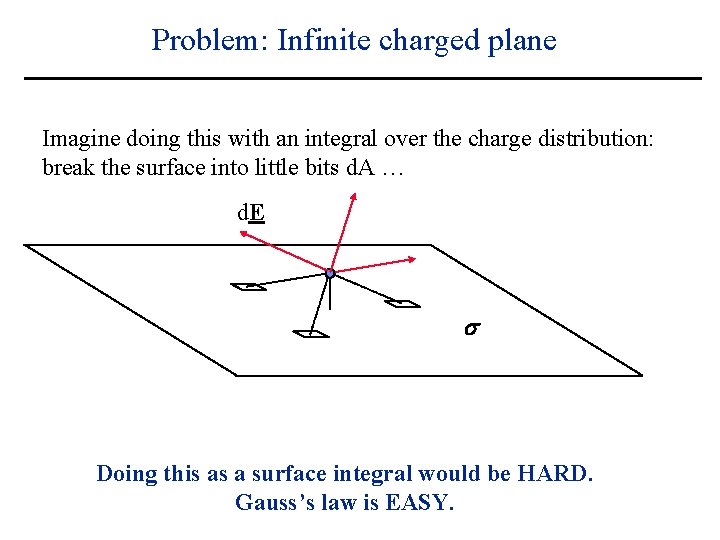
Problem: Infinite charged plane Imagine doing this with an integral over the charge distribution: break the surface into little bits d. A … d. E s Doing this as a surface integral would be HARD. Gauss’s law is EASY.

Example: An infinite thin line of charge. Charge per unit length l P y Find the electric field E at point P

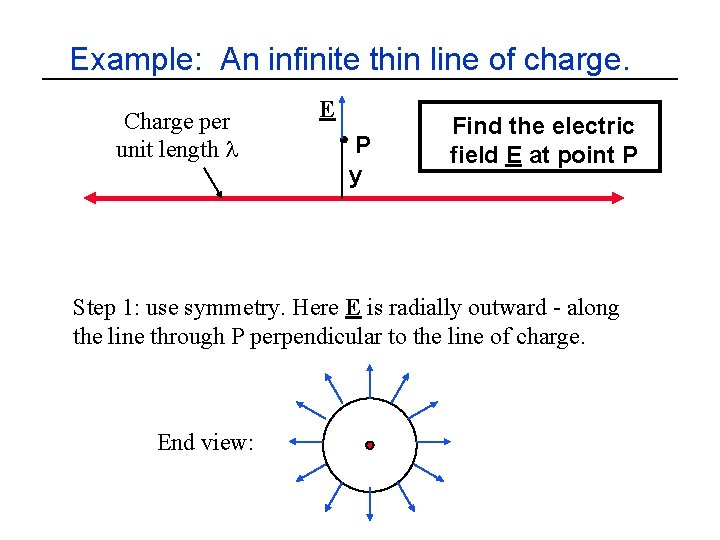
Example: An infinite thin line of charge. Charge per unit length l E P y Find the electric field E at point P Step 1: use symmetry. Here E is radially outward - along the line through P perpendicular to the line of charge. End view:

Example: An infinite thin line of charge. E P y Step 1: use symmetry. Here E is radially outward - along the line through P perpendicular to the line of charge. Step 2: choose a Gaussian surface - here a cylinder centered on the line of charge. Notice that E has the same magnitude at all points on this surface - and points radially outward.

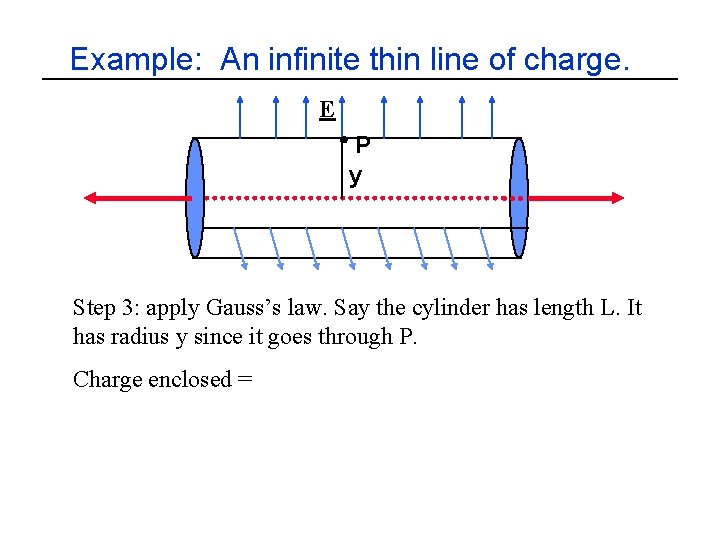
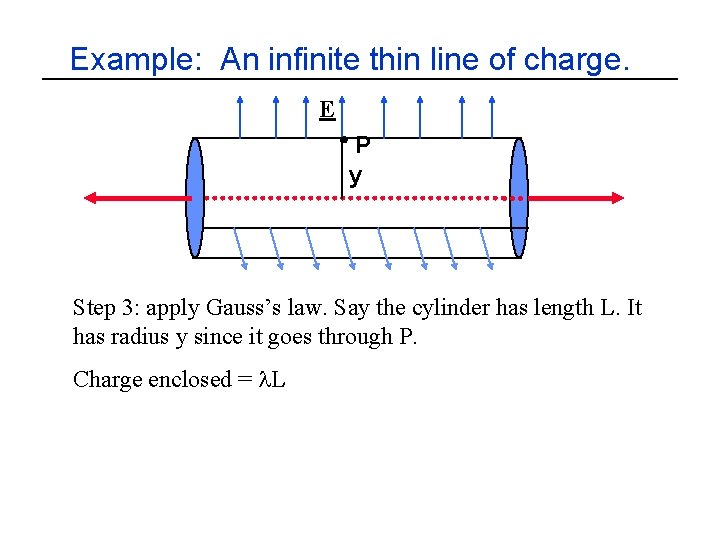
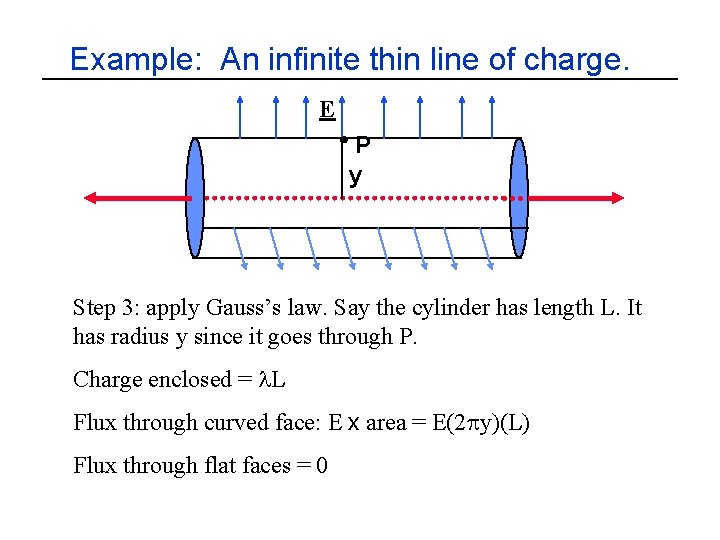
Example: An infinite thin line of charge. E P y Step 3: apply Gauss’s law. Say the cylinder has length L. It has radius y since it goes through P. Charge enclosed =

Example: An infinite thin line of charge. E P y Step 3: apply Gauss’s law. Say the cylinder has length L. It has radius y since it goes through P. Charge enclosed = l. L

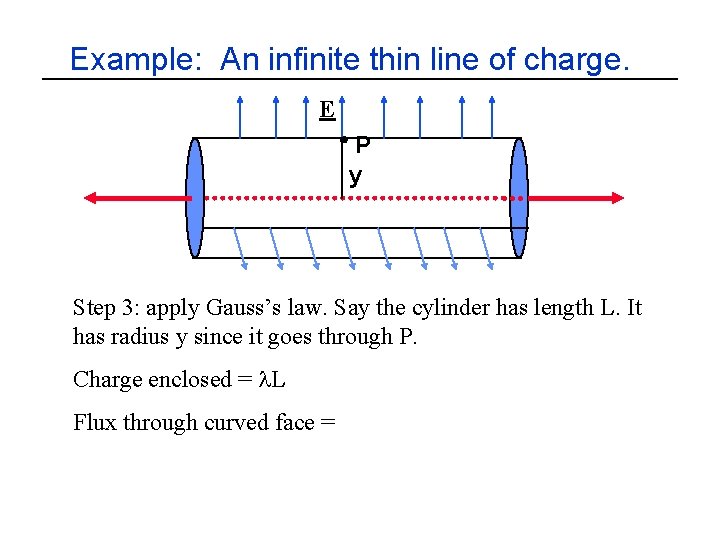
Example: An infinite thin line of charge. E P y Step 3: apply Gauss’s law. Say the cylinder has length L. It has radius y since it goes through P. Charge enclosed = l. L Flux through curved face =

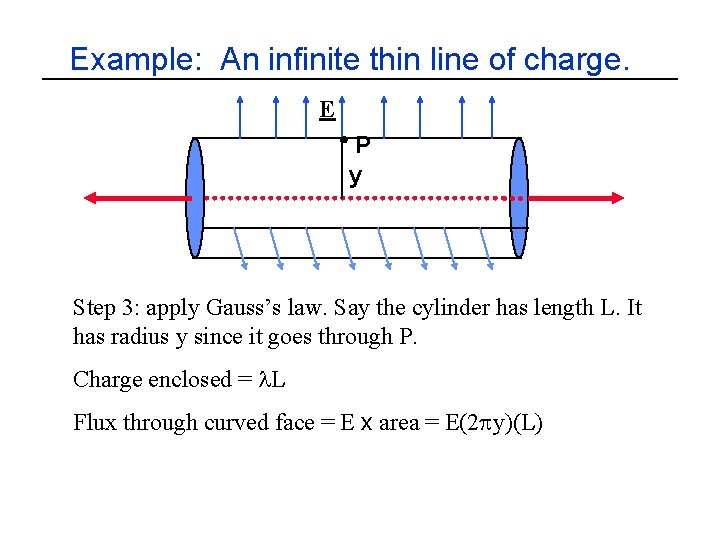
Example: An infinite thin line of charge. E P y Step 3: apply Gauss’s law. Say the cylinder has length L. It has radius y since it goes through P. Charge enclosed = l. L Flux through curved face = E x area = E(2 py)(L)

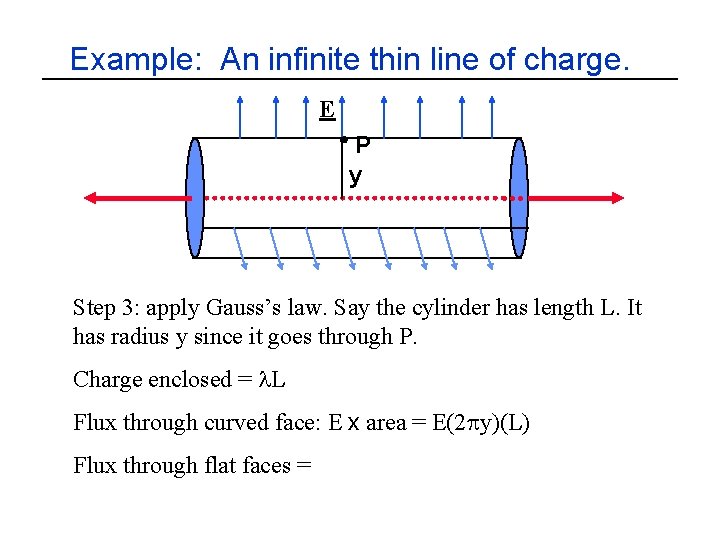
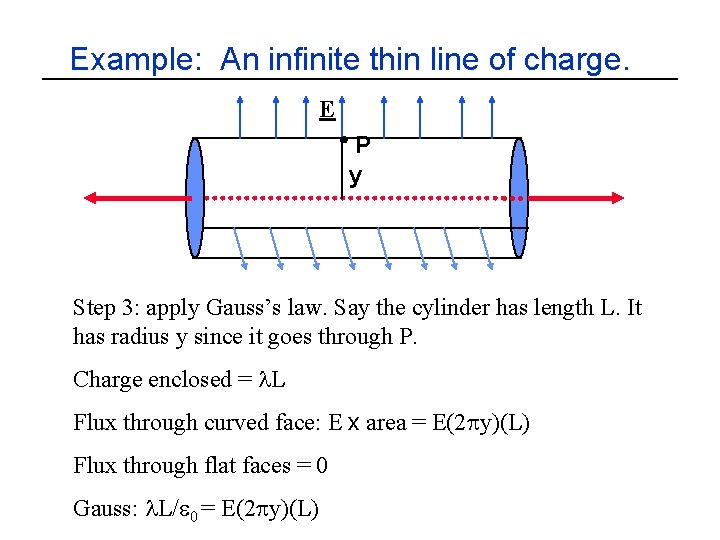
Example: An infinite thin line of charge. E P y Step 3: apply Gauss’s law. Say the cylinder has length L. It has radius y since it goes through P. Charge enclosed = l. L Flux through curved face: E x area = E(2 py)(L) Flux through flat faces =

Example: An infinite thin line of charge. E P y Step 3: apply Gauss’s law. Say the cylinder has length L. It has radius y since it goes through P. Charge enclosed = l. L Flux through curved face: E x area = E(2 py)(L) Flux through flat faces = 0

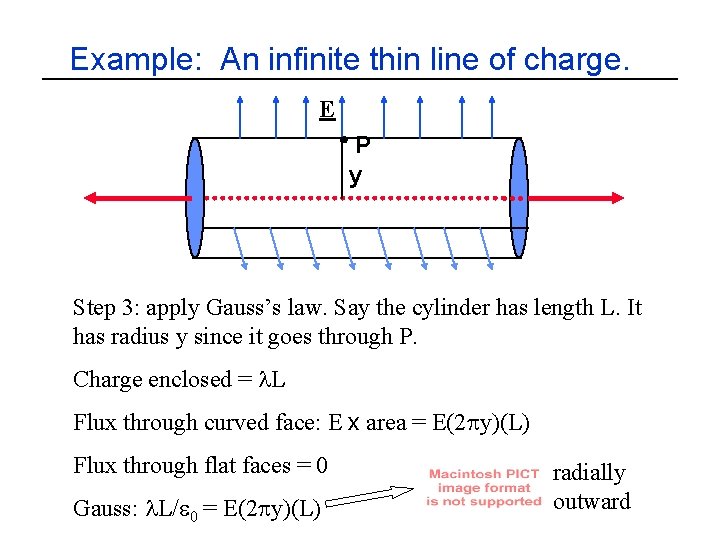
Example: An infinite thin line of charge. E P y Step 3: apply Gauss’s law. Say the cylinder has length L. It has radius y since it goes through P. Charge enclosed = l. L Flux through curved face: E x area = E(2 py)(L) Flux through flat faces = 0 Gauss: l. L/e 0 = E(2 py)(L)

Example: An infinite thin line of charge. E P y Step 3: apply Gauss’s law. Say the cylinder has length L. It has radius y since it goes through P. Charge enclosed = l. L Flux through curved face: E x area = E(2 py)(L) Flux through flat faces = 0 Gauss: l. L/e 0 = E(2 py)(L) radially outward

Conductors • A conductor is a material in which some of the electrons (~1 per atom) can move relatively freely. • Usually these are metals (Au, Cu, Ag, Al). • The conduction electrons tend to move together, like water in the ocean. An ordinary chunk of conductor is neutral, and the electrons, repelling one another and attracted by the background ions, spread uniformly. • If you place excess charge on a conductor, the charges move as far from each other as possible. • In a static situation, the electric field is zero everywhere inside a conductor. • In a static situation, all the excess charge (- or +) resides at the surface of a conductor.

Conductors Why is E=0 inside a conductor in equilibrium?

Conductors Why is E=0 inside a conductor in equilibrium? Conductors are full of free electrons, roughly one per cubic Angstrom. These are free to move. If E is nonzero in some region, then the conduction electrons there feel a force -e. E and start to move.

Conductors Why is E=0 inside a conductor in equilibrum? Conductors are full of free electrons, roughly one per cubic Angstrom. These are free to move. If E is nonzero in some region, then the conduction electrons there feel a force -e. E and start to move. In an electrostatics problem, the electrons adjust their positions until the force on every electron is zero (or else it would move!). That means when equilibrium is reached, E=0 everywhere inside a conductor.

Conductors Because E=0 inside, the inside of a conductor is neutral. Suppose there is an extra charge inside. Gauss’s law for the little spherical surface says there would be a nonzero E nearby. But there can’t be, within a metal! Consequently the interior of a metal is neutral. Any excess charge ends up on the surface.

Example: Charged Conducting Sphere Suppose you add an extra charge Q to a sphere of radius R. Find E everywhere.

Example: Charged Conducting Sphere Suppose you add an extra charge Q to a sphere of radius R. Find E everywhere. The excess charge Q goes to the surface, producing a surface charge s=Q/4 p. R 2 s

Example: Charged Conducting Sphere Suppose you add an extra charge Q to a sphere of radius R. Find E everywhere. The excess charge Q goes to the surface, producing a surface charge s=Q/4 p. R 2 s Outside: the spherical distribution acts as though it were all concentrated at the origin.

Example: Charged Conducting Sphere Suppose you add an extra charge Q to a sphere of radius R. Find E everywhere. The excess charge Q goes to the surface, producing a surface charge s=Q/4 p. R 2 s Outside: the spherical distribution acts as though it were all concentrated at the origin. So

Example: Charged Conducting Sphere Suppose you add an extra charge Q to a sphere of radius R. Find E everywhere. The excess charge Q goes to the surface, producing a surface charge s=Q/4 p. R 2 s Outside: the spherical distribution acts as though it were all concentrated at the origin. So Within a spherical shell the net electric field due to the shell is zero. So E(r)=0, r<R.

Conducting Spherical Shell with a Charge Inside Suppose you have a neutral conducting spherical shell of interior radius a and exterior radius b. Suppose there is a point charge q at the center of the cavity. Find E everywhere. b q a

Conducting Spherical Shell with a Charge Inside Suppose you have a neutral conducting spherical shell of interior radius a and exterior radius b. Suppose there is a point charge q at the center of the cavity. Find E everywhere. b q a In the cavity:

Conducting Spherical Shell with a Charge Inside Suppose you have a neutral conducting spherical shell of interior radius a and exterior radius b. Suppose there is a point charge q at the center of the cavity. Find E everywhere. b q a In the cavity:

Conducting Spherical Shell with a Charge Inside Suppose you have a neutral conducting spherical shell of interior radius a and exterior radius b. Suppose there is a point charge q at the center of the cavity. Find E everywhere. b q a In the cavity: Within the shell:

Conducting Spherical Shell with a Charge Inside Suppose you have a neutral conducting spherical shell of interior radius a and exterior radius b. Suppose there is a point charge q at the center of the cavity. Find E everywhere. b q a In the cavity: Within the shell:

Conducting Spherical Shell with a Charge Inside Suppose you have a neutral conducting spherical shell of interior radius a and exterior radius b. Suppose there is a point charge q at the center of the cavity. Find E everywhere. b q a In the cavity: Within the shell: Outside the shell:

Conducting Spherical Shell with a Charge Inside Suppose you have a neutral conducting spherical shell of interior radius a and exterior radius b. Suppose there is a point charge q at the center of the cavity. Find E everywhere. b q a In the cavity: Within the shell: Outside the shell: the only charge enclosed by a Gaussian sphere is q, so it must be the case that

Conducting Spherical Shell with a Charge Inside Suppose you have a neutral conducting spherical shell of interior radius a and exterior radius b. Suppose there is a point charge q at the center of the cavity. Find E everywhere. b q a In the cavity: Within the shell: Outside the shell: the only charge enclosed by a Gaussian sphere is q, so it must be the case that

Conducting Spherical Shell with a Charge Inside Suppose you have a neutral conducting spherical shell of interior radius a and exterior radius b. Suppose there is a point charge q at the center of the cavity. Find E everywhere. b q a In the cavity: Within the shell: Outside the shell: the only charge enclosed by a Gaussian sphere is q, so it must be the case that This result is more interesting if we think about why it happens.

Conducting Spherical Shell with a Charge Inside The key point is that within the conducting shell E(r)=0 (a<r<b). Draw a Gaussian sphere of radius r lying within the shell. q r

Conducting Spherical Shell with a Charge Inside The key point is that within the conducting shell E(r)=0 (a<r<b). Draw a Gaussian sphere of radius r lying within the shell. Gauss’s law says that E(4 pr 2)=Qenc/e 0, so that within the shell q r

Conducting Spherical Shell with a Charge Inside The key point is that within the conducting shell E(r)=0 (a<r<b). Draw a Gaussian sphere of radius r lying within the shell. Gauss’s law says that E(4 pr 2)=Qenc/e 0, so that within the shell q r What is Qenc?

Conducting Spherical Shell with a Charge Inside The key point is that within the conducting shell E(r)=0 (a<r<b). Draw a Gaussian sphere of radius r lying within the shell. Gauss’s law says that E(4 pr 2)=Qenc/e 0, so that within the shell q r What is Qenc? At first glance apparently q. But this cannot be right. The only way to get E=0 is if Qenc=0.

Conducting Spherical Shell with a Charge Inside The key point is that within the conducting shell E(r)=0 (a<r<b). Draw a Gaussian sphere of radius r lying within the shell. Gauss’s law says that E(4 pr 2)=Qenc/e 0, so that within the shell q r What is Qenc? At first glance apparently q. But this cannot be right. The only way to get E=0 is if Qenc=0. And the only way Qenc can be zero is if the central charge q attracts (“induces”) a charge -q to the inner surface of the shell - that is, induces a surface charge density s=-q/4 pa 2.

Conducting Spherical Shell with a Charge Inside With the induced surface charge, the total charge enclosed by the Gaussian sphere of radius r is q+(-q)=0, so indeed E=0 in the shell. - - - q+ - - -

Conducting Spherical Shell with a Charge Inside With the induced surface charge, the total charge enclosed by the Gaussian sphere of radius r is q+(-q)=0, so indeed E=0 in the shell. - - - q+ - - But the shell is neutral. -

Conducting Spherical Shell with a Charge Inside With the induced surface charge, the total charge enclosed by the Gaussian sphere of radius r is q+(-q)=0, so indeed E=0 in the shell. - - - q+ - - - But the shell is neutral. The only way to have a charge -q on the inner surface and still be neutral is if there is also a surface charge on the outer surface, a total charge +q.

Conducting Spherical Shell with a Charge Inside With the induced surface charge, the total charge enclosed by the Gaussian sphere of radius r is q+(-q)=0, so indeed E=0 in the shell. + + + - - q+ - + + + - - - - + + + But the shell is neutral. The only way to have a charge -q on the inner surface and still be neutral is if there is also a surface charge on the outer surface, a total charge +q.

Conducting Spherical Shell with a Charge Inside With the induced surface charge, the total charge enclosed by the Gaussian sphere of radius r is q+(-q)=0, so indeed E=0 in the shell. + + + - - q+ - + + + - - - - + But the shell is neutral. The only way to have a charge -q on the inner surface and still be neutral is if there is also a surface charge on the outer surface, a total charge +q. + + Hence a Gaussian surface drawn outside the shell encloses a charge q+(-q)+q=q, as though the shell were not even there.

Problem: Charged coaxial cable This picture is a cross section of an infinitely long line of charge, surrounded by an infinitely long cylindrical conductor. Find E. This represents the line of charge. Say it has a linear charge density of l (some number of C/m). b a Use symmetry! This is the cylindrical conductor. It has inner radius a, and outer radius b. Clearly E points straight out, and its amplitude depends only on r.

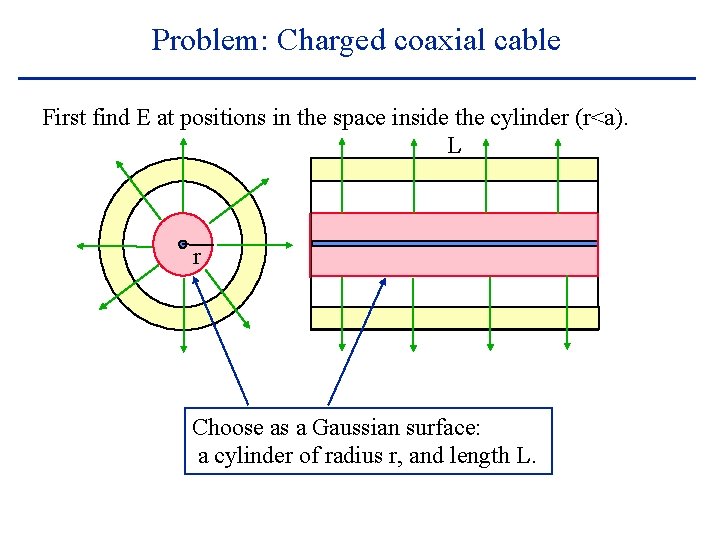
Problem: Charged coaxial cable First find E at positions in the space inside the cylinder (r<a). L r Choose as a Gaussian surface: a cylinder of radius r, and length L.

Problem: Charged coaxial cable First find E at positions in the space inside the cylinder (r<a). L r What is the charge enclosed? l. L What is the flux through the end caps? zero (cos 900) What is the flux through the curved face? E x (area) = E(2 pr. L) Total flux = E(2 pr. L) Gauss’s law E(2 pr. L) = l. L/e 0 so E(r) = l/ 2 pre 0

Problem: Charged coaxial cable Now find E at positions within the cylinder (a<r<b). There’s no work to do: within a conductor E=0. Still, we can learn something from Gauss’s law. Make the same kind of cylindrical Gaussian surface. Now the curved side is entirely within the conductor, where E=0; hence the flux is zero. + r Thus the total charge enclosed by this surface must be zero.

Problem: Charged coaxial cable There must be a net charge per unit length -l attracted to the inner surface of the metal, so that the total charge enclosed by this Gaussian surface is zero. - - + - r - -

Problem: Charged coaxial cable There must be a net charge per unit length –l attracted to the inner surface of the metal so that the total charge enclosed by this Gaussian surface is zero. + + + - - + + r + - And since the cylinder is neutral, these negative charges must have come from the outer surface. So the outer surface has a charge density per unit length of +l spread around the outer perimeter. + So what is the field for r>b?