Gases Pressure Its Measurement Pressure Gases exert pressure

Gases Pressure & Its Measurement

Pressure • Gases exert pressure on their surroundings. • Ex. Balloon filled with air – Air pushes against the elastic sides of the balloon and keeps it firm

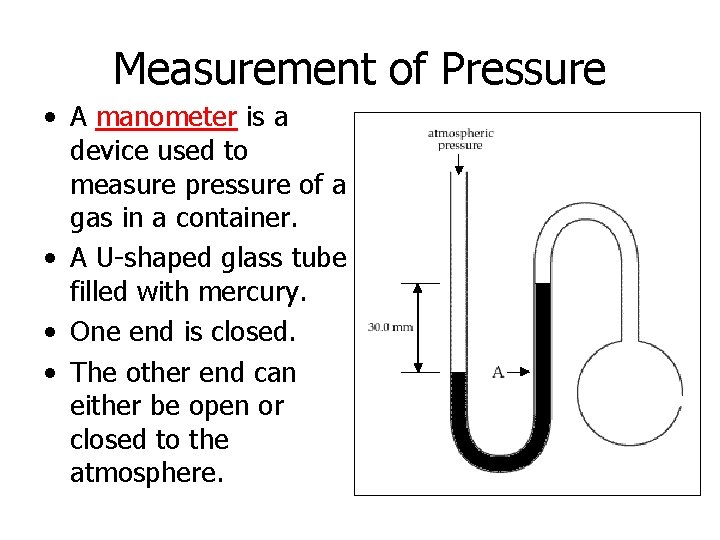
Measurement of Pressure • A manometer is a device used to measure pressure of a gas in a container. • A U-shaped glass tube filled with mercury. • One end is closed. • The other end can either be open or closed to the atmosphere.

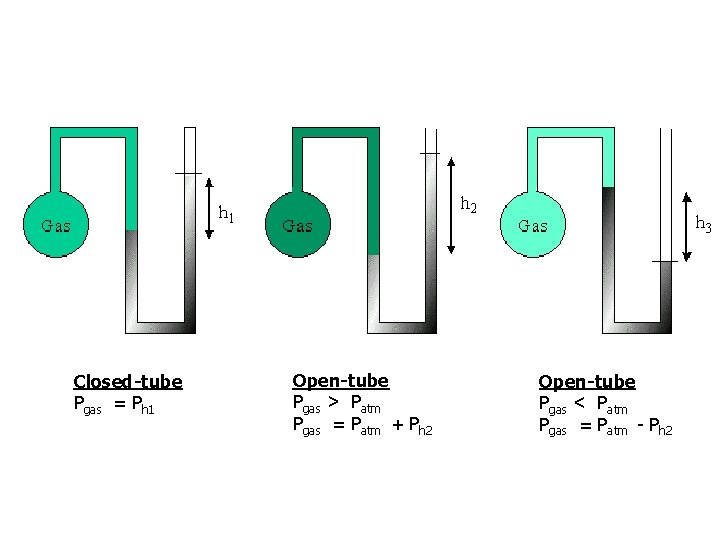
To Measure the Pressure of Gas in a Container In an open-tube manometer: 1) When the pressure of the gas is greater than atmospheric pressure: Gas pressure = atmospheric pressure + h (height of the Hg) 2) When the pressure of the gas is less than atmospheric pressure: Gas pressure = atmospheric pressure - h (height of the Hg) In a closed-tube manometer: • Closed-tube manometers look similar to regular manometers except that both ends are sealed and contains a vacuum. • Difference in mercury levels is equal to the pressure of the gas.

Closed-tube Pgas = Ph 1 Open-tube Pgas > Patm Pgas = Patm + Ph 2 Open-tube Pgas < Patm Pgas = Patm - Ph 2

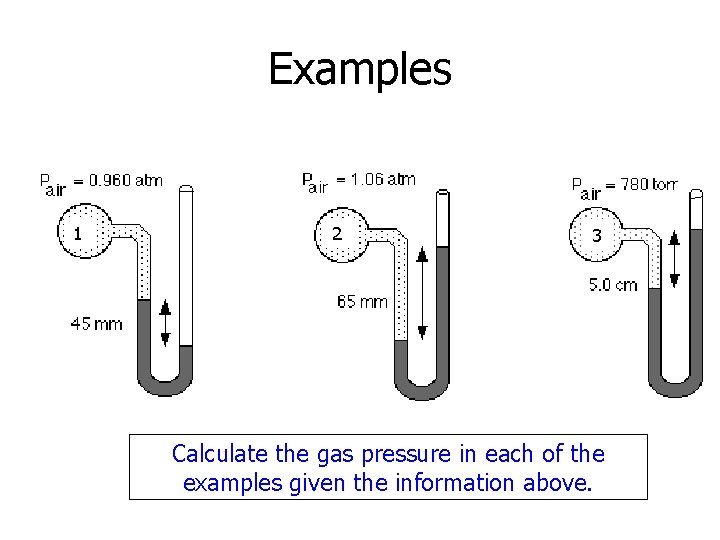
Examples 1 2 3 Calculate the gas pressure in each of the examples given the information above.

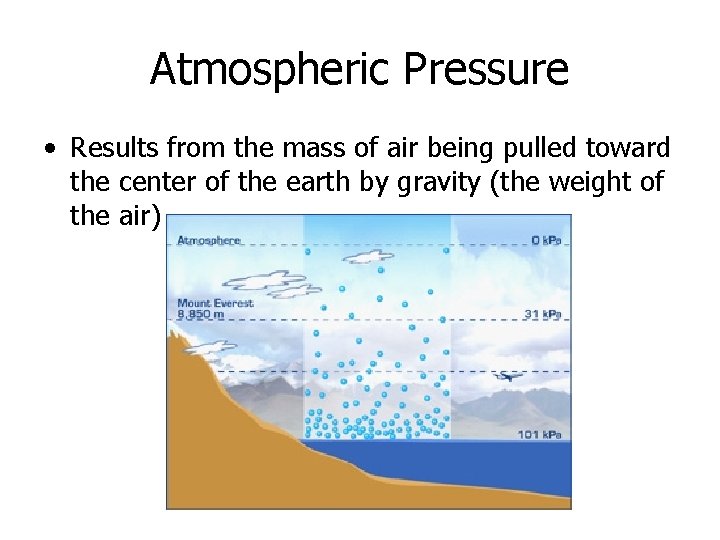
Atmospheric Pressure • Results from the mass of air being pulled toward the center of the earth by gravity (the weight of the air)

Measurement of Atmospheric Pressure • A barometer is a device that measures atmospheric pressure • A glass tube is filled with mercury and inverted in a dish of mercury at sea level.

Units of Pressure Unit of Pressure Abbreviation Equivalent torres torr 760 torr atmospheres atm 1 atm kilopascals k. Pa 101. 3 k. Pa millimeters of mercury mm Hg 760 mm Hg pounds per square inch psi or lb/in 2 14. 7 psi inches of mercury in Hg 29. 92 in Hg These quantities of pressure all equivalent to each other.

Examples Solve the following problems involving pressure conversions. 1. Today’s weather report stated that the atmospheric pressure as 0. 94 atm. What is the atmospheric pressure in mm Hg? 2. The air pressure inside an inflated rubber balloon is 0. 1 atm. What is this pressure in psi? 3. The atmospheric pressure atop Mt. Everest is approximately 30 k. Pa. What is this pressure in atmospheres?

Gases Boyle’s Law

Factors that Describe Gases • Four variables are generally used to describe a gas. The variables and their common units are 1. 2. 3. 4. pressure (P) in kilopascals volume (V) in liters temperature (T) in kelvins the number of moles (n)

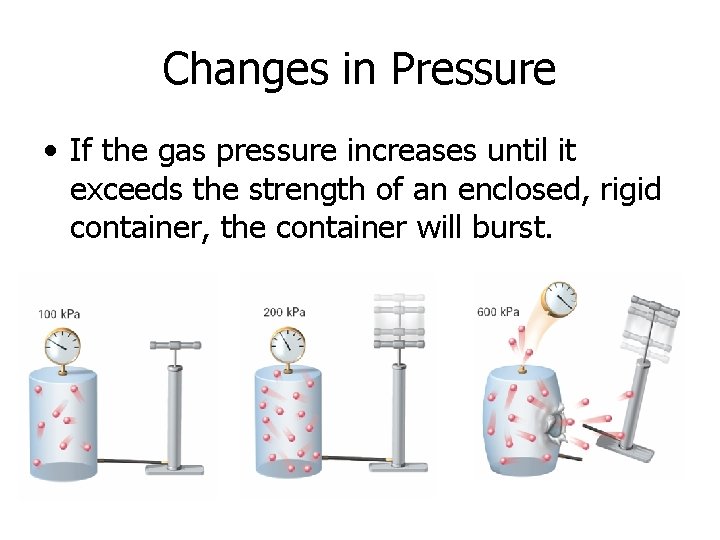
Changes in Pressure • If the gas pressure increases until it exceeds the strength of an enclosed, rigid container, the container will burst.

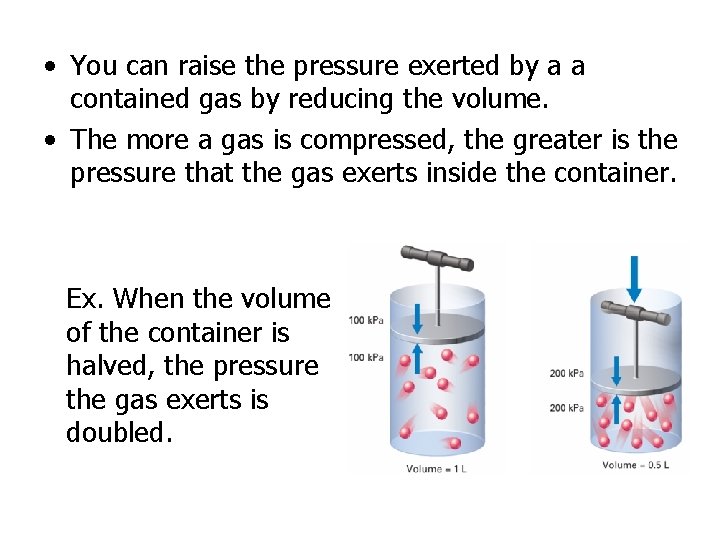
• You can raise the pressure exerted by a a contained gas by reducing the volume. • The more a gas is compressed, the greater is the pressure that the gas exerts inside the container. Ex. When the volume of the container is halved, the pressure the gas exerts is doubled.

Pressure is Related to Volume of a Gas Pressure Volume P x. V 1. 0 atm 2 L 2 2. 0 atm 1 L 2 3. 0 atm 4. 0 atm 0. 67 L 0. 5 L 2 2 P 1 V 1 = P 2 V 2 = P 3 V 3 = P 4 V 4 = K

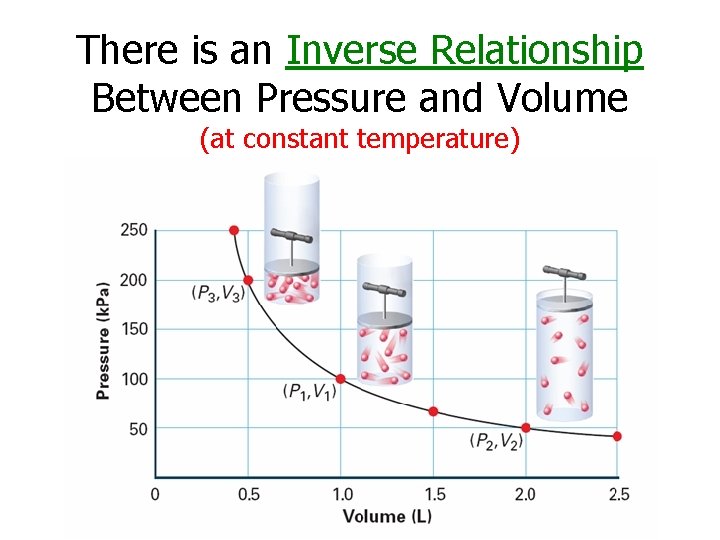
There is an Inverse Relationship Between Pressure and Volume (at constant temperature)

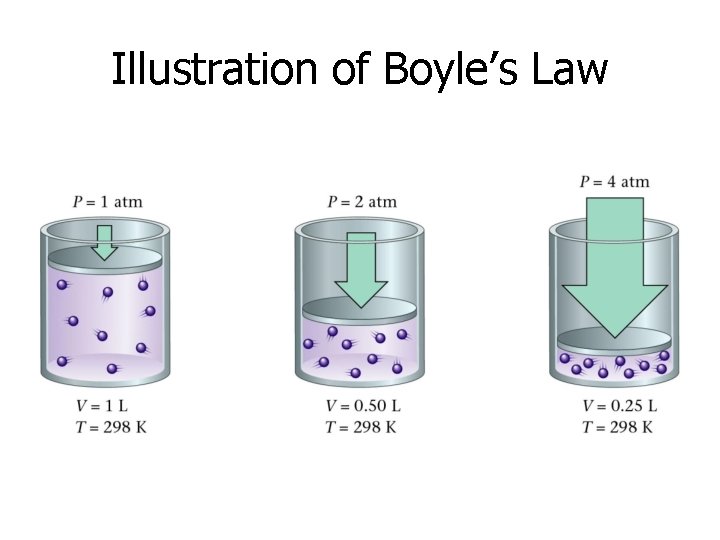
Boyle’s Law States that for a given mass of gas at constant temperature, the volume of the gas varies inversely with pressure.

Illustration of Boyle’s Law

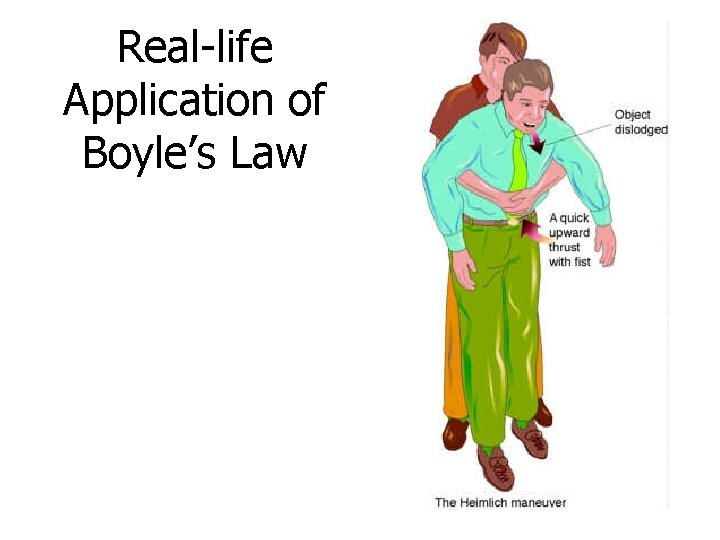
Real-life Application of Boyle’s Law

Try These! 1. A balloon contains 30. 0 L of helium gas at 101. 3 k. Pa. What is the volume of the helium when the balloon rises to an altitude where the pressure is only 25. 0 k. Pa? Assume that the temperature remains constant.

2. If the volume occupied by the air inn a bicycle pump is 525 cm 3, and the pressure changes from 73. 2 k. Pa to 122. 5 k. Pa as the piston is pushed down, what is the new volume occupied by the air?

3. If the volume of the air pump used to inflate a football decreases from 425 cm 3 to 305 cm 3, and the original pressure was 92. 5 k. Pa, what is the new air pressure in the pump?

Gases Charles’s Law

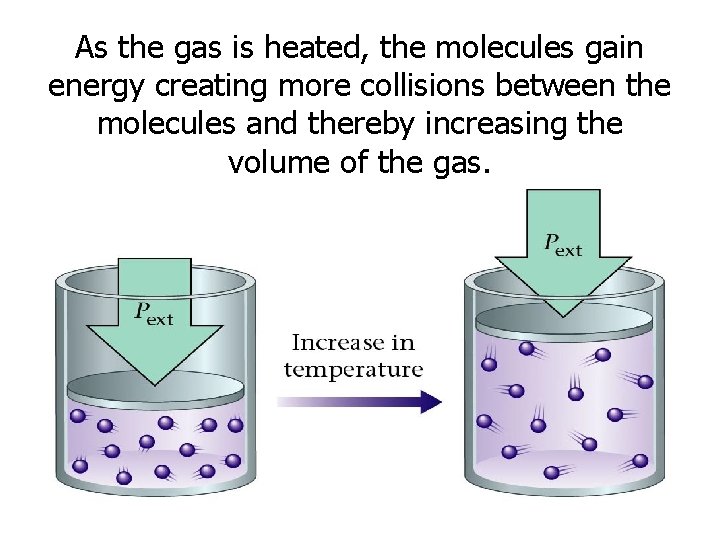
Changes in Temperature • As the temperature of an enclosed gas increases, the volume increases, if the pressure is constant.

As the gas is heated, the molecules gain energy creating more collisions between the molecules and thereby increasing the volume of the gas.

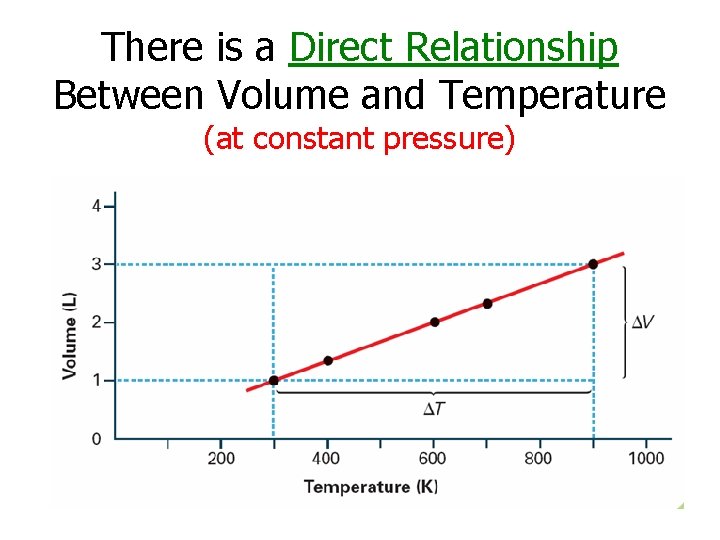
Charles’s Law States that the volume of a fixed mass of gas is directly proportional to its Kelvin temperature if the pressure is kept constant.

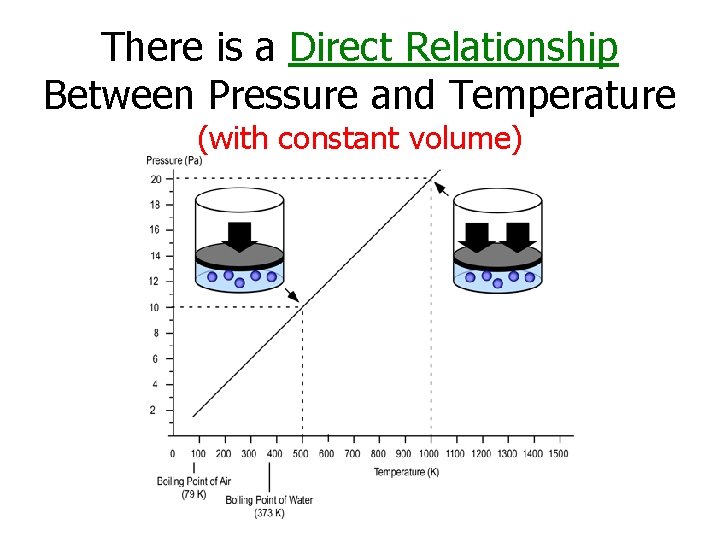
There is a Direct Relationship Between Volume and Temperature (at constant pressure)

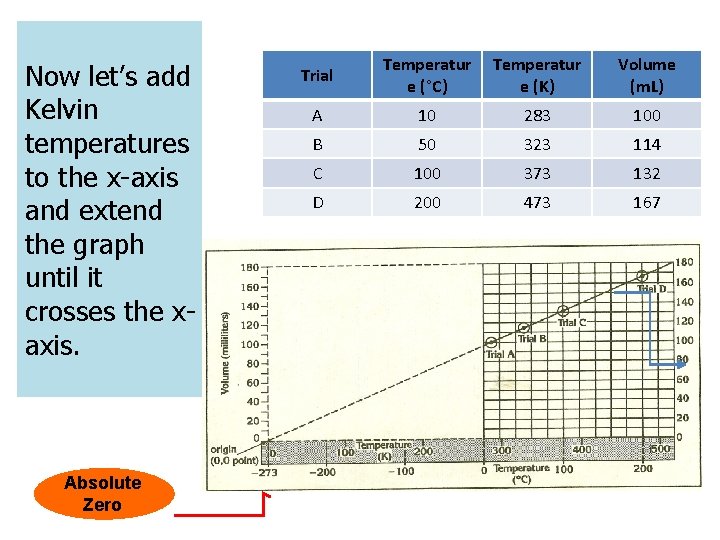
Kelvin Temperature Scale Remember: Boiling pt of water is 373 K Melting pt of water is 273 K Absolute zero (0 K) is -273°C How was this value determined?

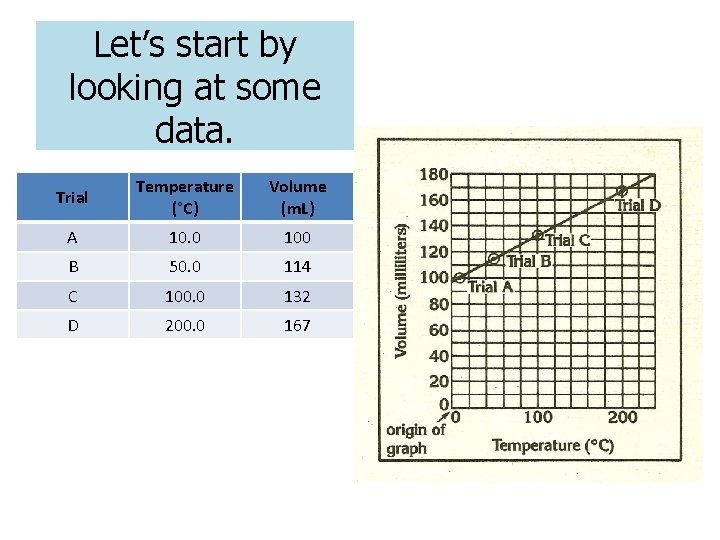
Let’s start by looking at some data. Trial Temperature (°C) Volume (m. L) A 10. 0 100 B 50. 0 114 C 100. 0 132 D 200. 0 167

Now let’s add Kelvin temperatures to the x-axis and extend the graph until it crosses the xaxis. Absolute Zero Trial Temperatur e (°C) Temperatur e (K) Volume (m. L) A 10 283 100 B 50 323 114 C 100 373 132 D 200 473 167

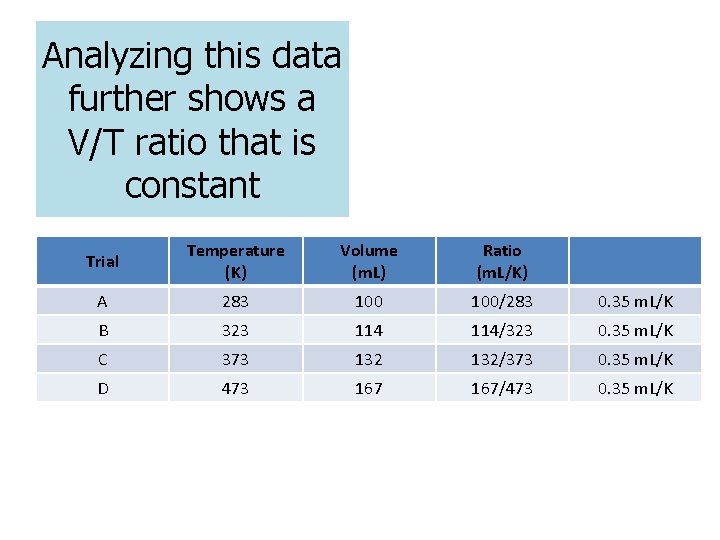
Analyzing this data further shows a V/T ratio that is constant Trial Temperature (K) Volume (m. L) Ratio (m. L/K) A 283 100/283 0. 35 m. L/K B 323 114/323 0. 35 m. L/K C 373 132/373 0. 35 m. L/K D 473 167/473 0. 35 m. L/K

Try These! 1. A balloon inflated in a room at 24°C has a volume of 4. 00 L. The balloon is then heated to a temperature of 58°C. What is the new volume if the pressure remains constant?

2. Calculate the final volume when a 75. 0 m. L sample of a gas is heated from 5°C to 60°C at constant pressure.

3. A 5. 00 L sample of a gas at 20°C is to be heated at constant pressure until it reaches a volume of 8. 00 L. To what Kelvin temperature must this sample be heated?

Gases Gay-Lussac’s Law Combined Gas Law

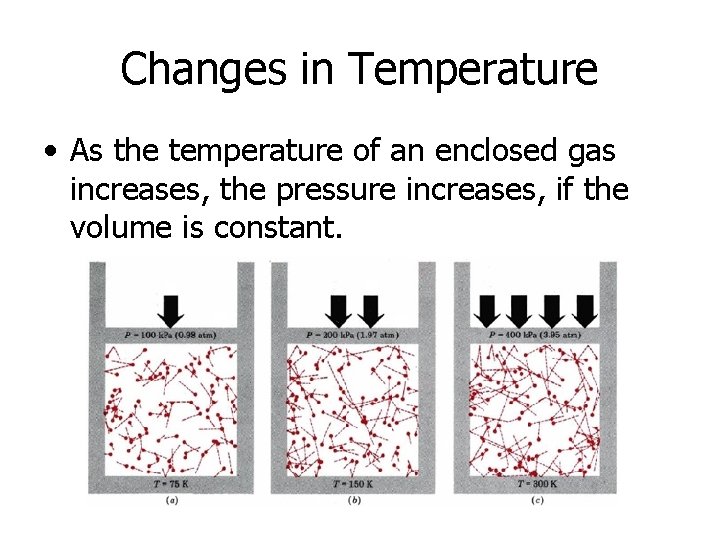
Changes in Temperature • As the temperature of an enclosed gas increases, the pressure increases, if the volume is constant.

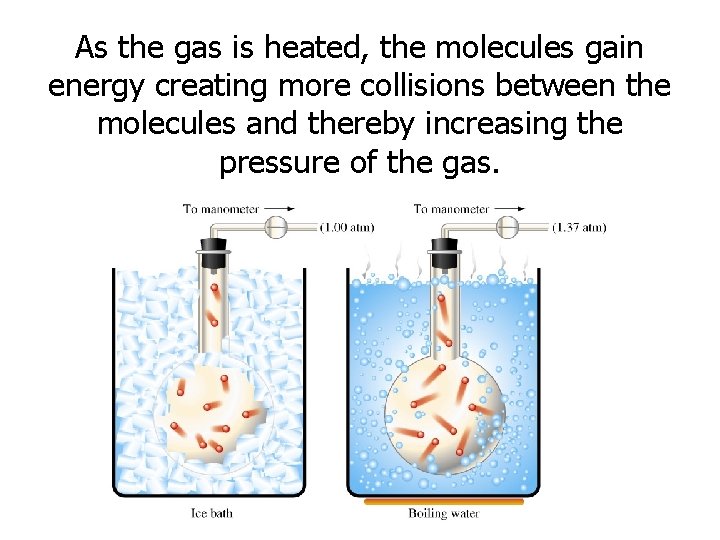
As the gas is heated, the molecules gain energy creating more collisions between the molecules and thereby increasing the pressure of the gas.

Gay-Lussac’s Law States that the pressure of a gas is directly proportional to its Kelvin temperature if the volume remains constant.

A pressure cooker demonstrates Gay-Lussac’s Law

There is a Direct Relationship Between Pressure and Temperature (with constant volume)

Try These! 1. A cylinder contains a gas which has a pressure of 125 k. Pa at a temperature of 200 K. Find the temperature of the gas when it has a pressure of 100 k. Pa.

2. Find the final pressure of a gas at 150 K, if the pressure of a gas is 210 k. Pa at 120 K.

3. 10. 0 L of a gas is found to exert 97. 0 k. Pa at 25. 0°C. What would be the required temperature to change the pressure to standard pressure?

Combined Gas Law • Describes the relationship among the pressure, temperature, and volume of an enclosed gas. (Combines Boyle’s Law, Charles’s Law, Gay-Lussac’s Law)

Try These! 1. 2. 00 L of a gas is collected at 25°C and 745. 0 mm Hg. What is the volume at STP?

2. A sample of a helium gas has a volume of 600. m. L and a pressure of 1. 50 atm at 298 K. What is the new pressure when the temperature is changed to 350 K and the volume is decreased to 250. m. L?

3. A 63. 5 m. L sample of gas at 300 K and 1. 2 atm is compressed to 25. 8 m. L at a temperature of 200 K. What is the final pressure of the gas?

Gases Ideal Gas Law Density of Gases at STP

“Ideal” Gases • Exhibit certain theoretical properties: 1. Obey all of the gas laws under all conditions • • all collisions between atoms or molecules are perfectly elastic there are no intermolecular attractive forces between atoms or molecules all the internal energy is in the form of kinetic energy any change in internal energy is accompanied by a change in temperature 2. In reality, there are no gases that fit this definition perfectly. We assume that gases are ideal to simplify our calculations.

Ideal Gas Law • Describes the relationship among the pressure, temperature, volume, and number of moles of an enclosed gas. PV = n. RT P = Pressure (in k. Pa or atm)V = Volume (in L) T = Temperature (in K) n = moles R = 8. 31 k. Pa • L or R =. 0821 atm • L K • mol R is constant. If we are given three of P, V, n, or T, we can solve for the unknown value.

• From the ideal gas law equation PV = n. RT we can also derive another equation. M) PV = n. RT PV = g RT M PM = g RT V PM = d. RT (n = g/M) (multiply both sides by (g/V = d)

Try These! 1) What volume is needed to store 0. 050 moles of helium gas at 202. 6 k. Pa and 400 K?

2) What pressure will be exerted by 20. 16 g hydrogen gas in a 7. 5 L cylinder at 20 o. C?

3) A 50 L cylinder is filled with argon gas to a pressure of 100. 0 atm at 30 o. C. How many moles of argon gas are in the cylinder?

4) How many grams of Cl 2(g) can be stored in a 10. 0 L container at 1000 k. Pa and 30°C?

5) At 150°C and 100 k. Pa, 1. 00 L of a compound has a mass of 2. 506 g. Calculate its molar mass.

6) 98 m. L of an unknown gas weighs 0. 087 g at STP. Calculate the molar mass of the gas. Can you determine the identity of this unknown gas?

Density of a Gas Density = mass (g) volume (m. L) = mass of 1 mole volume of 1 mole = gfm____ molar volume = gfm__ 22. 4 L

Try These! 1) What is the density of O 2 at STP? 2) What is the density of Cl 2 at STP? 3) What is the density of Kr at STP?

Gases Kinetic Molecular Theory Avogadro’s Hypothesis Graham’s Law Dalton’s Law

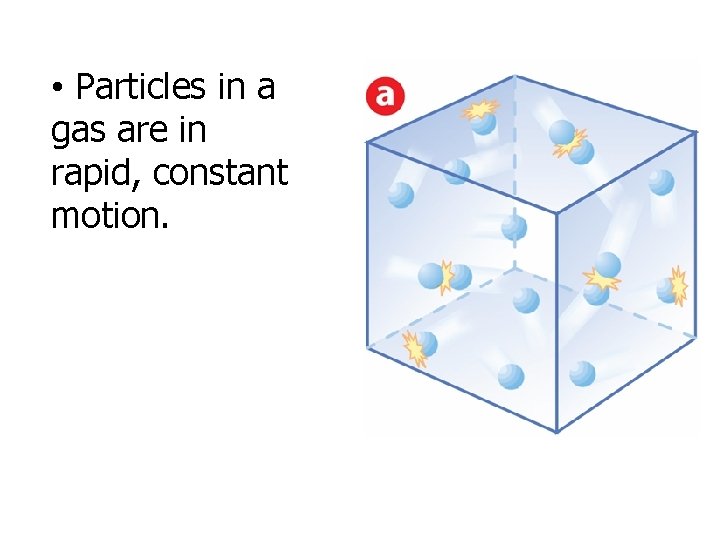
Kinetic Theory and a Model for Gases • The energy an object has because of its motion is called kinetic energy. • According to the kinetic theory, all matter consists of tiny particles that are in constant motion.

• Particles in a gas are in rapid, constant motion.

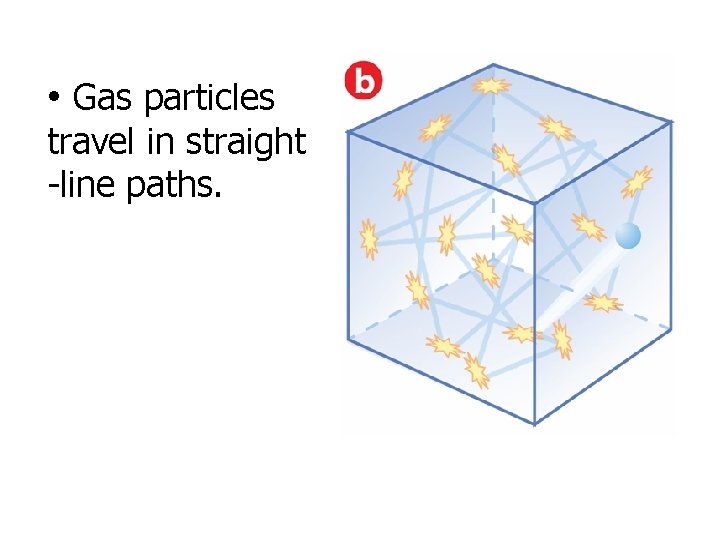
• Gas particles travel in straight -line paths.

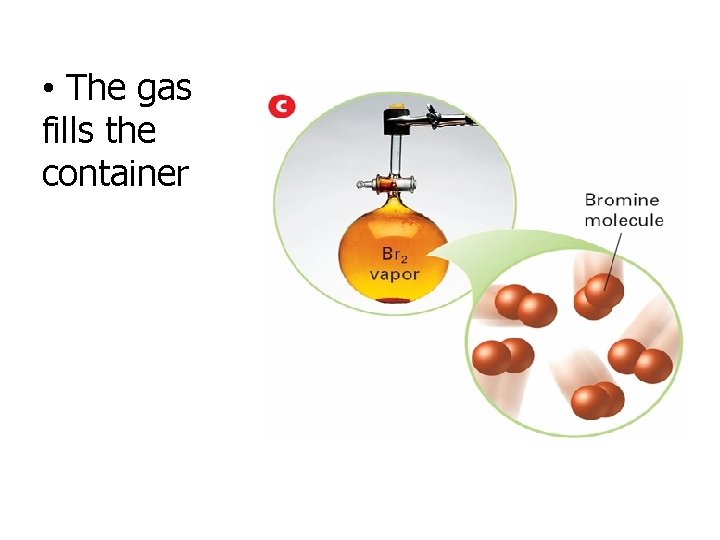
• The gas fills the container

Kinetic Theory of Gases • • • Gas laws describe how IDEAL gases behave Most gases obey these laws at STP REAL gases behave slightly differently under certain conditions 1. 2. • High Pressure Low Temperature Gases behave most like IDEAL gases under: 1. 2. Low Pressure High Temperature Remember: “PLIGHT”

Main Assumptions of the Gas Laws (There are 5!!!) 1. 2. 3. Gas molecules are very far apart (this explains why gases can be compressed) Gas particles are in continuous, straight-line, rapid motion (the pressure exerted by a gas is the result of this motion) Collisions between gas molecules are completely elastic (No loss of energy, therefore, the pressure of an enclosed gas remains the same if its temp & volume do not change)

4. Molecules of a gas do NOT attract or repel each other (there are no forces of attraction between gas particles) 5. The average kinetic energy of the particles is directly proportional to the Kelvin temperature Real gas behavior approaches ideal gas behavior when we can keep the particles far apart – that is, when the temperature is high and the pressure is low. Gases lose ideal behavior when the temperature is very low and the pressure is very high. WHY?

Real Gases • As pressure increases, the volume decreases BUT at some point the molecules are very close together and cannot be compressed any more. • At high pressure, attractive forces between gas molecules come into play because particles are closer together. • At low temperature, molecules are moving slower, so attractive forces come into play. This explains why at high pressure, volumes tend to be greater than predicted by Boyle’s Law. This explains why the volume of a gas is less at high pressure & low temperature than what would be predicted by Boyle’s & Charles’ laws

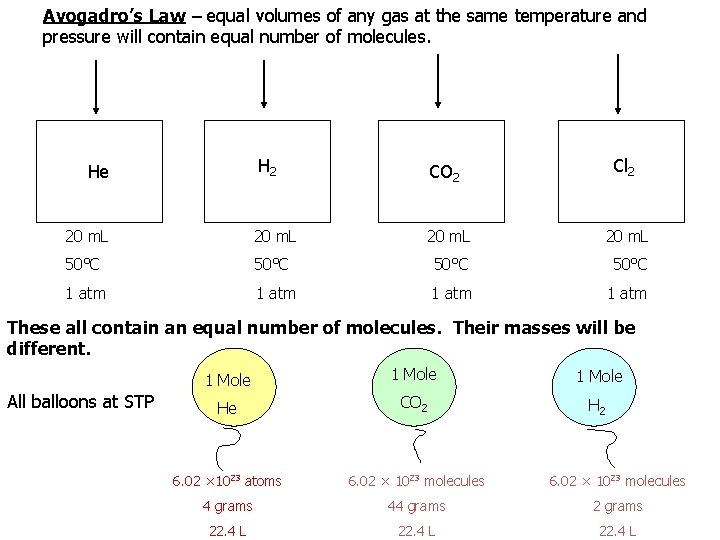
Avogadro’s Hypothesis • One of the basic concepts of chemistry “SAME – SAME” “Equal volumes of different gases at the same temperature and pressure contain the same number of molecules” 1 mole = 22. 4 liters = 6. 02 x 10 23 particles

Avogadro’s Law – equal volumes of any gas at the same temperature and pressure will contain equal number of molecules. H 2 CO 2 20 m. L 50°C 1 atm He Cl 2 These all contain an equal number of molecules. Their masses will be different. All balloons at STP 1 Mole He CO 2 H 2 6. 02 × 1023 atoms 6. 02 × 1023 molecules 4 grams 44 grams 22. 4 L

Example: Suppose we have a 12. 2 L sample containing 0. 50 mol of oxygen gas, O 2, at a pressure of 1 atm and a temperature of 25°C. If all of this O 2 is converted to O 3, at the same temperature and pressure, what will be the volume of the ozone formed? 3 O 2(g) 2 O 3(g) V 1 = V 2 n 1 n 2 so… 0. 50 mol O 2 x 2 mol O 3 = 0. 33 mol O 3 3 mol O 2 12. 2 L = V 2____ 0. 50 mol 0. 33 mol V 2 = 8. 1 L

Try This!!! Consider two samples of nitrogen gas (composed of N 2 molecules). Sample 1 contains 1. 5 mol of N 2 and has a volume of 36. 7 L at 25°C and 1 atm. Sample 2 has a volume of 16. 5 L at 25°C and 1 atm. Calculate the number of moles of N 2 in Sample 2.

Graham’s Law of Effusion • Effusion is the passing of gas molecules through a small hole in a container where no collisions occur between the molecules as they are passing through. • The random motion of the molecules prevent them from avoiding the small hole States that a gas will effuse at a rate that is inversely proportional to the square root of its molecular mass. Rate 1 = Rate 2 • Less dense gases will effuse faster Ex. Balloons do not stay inflated with gases forever • Helium filled balloon • Hydrogen filled balloon MM 2 MM 1

Example: If equal amounts of helium and argon are placed in a porous container and allowed to escape, which gas will escape faster and how much faster? MMHe = 4. 00 MMAr = 39. 95 x = 1 39. 95 4. 00 = 3. 16 times faster; He If the argon takes 20 sec to effuse, how long would it take for He? 20 sec Ar = 6. 33 sec for He to effuse 3. 16

Example: What is the molecular mass of a gas which diffuses 1/50 as fast as hydrogen? MMH 2 = 2. 02 MMother = x 1 = 50 1 2500 = 2. 02 x (square both sides) 2. 02 x (solve for x) X = 5050 g/mol

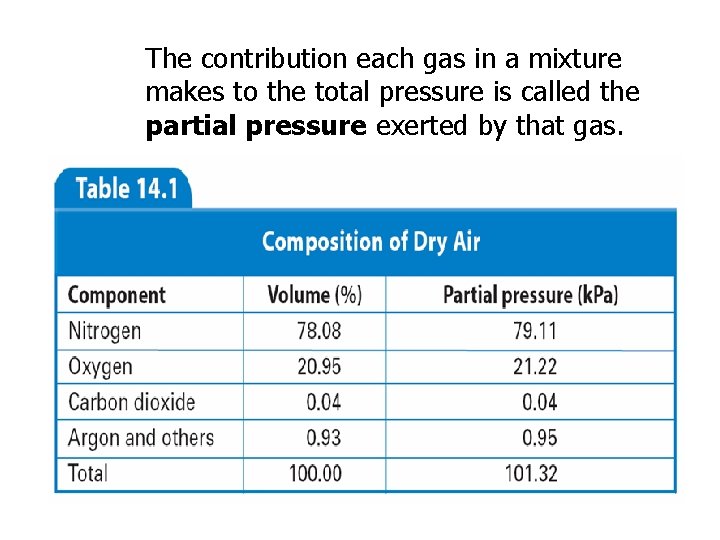
Dalton’s Law of Partial Pressure In a mixture of gases, the total pressure is equal to the sum of the pressures that each gas would exert by itself. PT = P 1 + P 2 + P 3 + …

Three gases are combined in container T

The contribution each gas in a mixture makes to the total pressure is called the partial pressure exerted by that gas.

The partial pressure of oxygen must be 10. 67 k. Pa or higher to support respiration in humans. The climber below needs an oxygen mask and a cylinder of compressed oxygen to survive.

Example: Air contains oxygen, nitrogen, carbon dioxide, and trace amounts of other gases. What is the partial pressure of oxygen (PO 2) at 101. 30 k. Pa of total pressure if the partial pressures of nitrogen, carbon dioxide, and other gases are 79. 10 k. Pa, 0. 040 k. Pa, and 0. 94 k. Pa, respectively? Ptotal = P 1 + P 2 + P 3 + … Ptotal = PO 2 + PN 2 + PCO 2 + Pother 101. 30 k. Pa = PO 2 + 79. 10 k. Pa + 0. 040 k. Pa + 0. 94 k. Pa PO 2 = 21. 22 k. Pa

Example: A container is filled with 5. 00 moles of nitrogen, 2. 00 moles of oxygen, and 4. 00 moles of hydrogen. If the mixture is at STP, what is the partial pressure of the hydrogen? N 2 = 5. 00 moles O 2 = 2. 00 moles H 2 = 4. 00 moles PH 2 = 4. 00 moles = x 11. 0 moles 101. 3 k. Pa 11 x = (4)(101. 3) PH 2 = x = 36. 8 k. Pa

Example: A 25. 0 m. L sample of nitrogen is collected over water at 20°C and 720. 0 torr pressure. What is the volume of the dry gas at STP? (Vapor pressure of water at 20°C = 17. 5 torr) PT = PN 2 + PH 2 O 720. 0 torr = PN 2 + 17. 5 torr PN 2 = 702. 5 torr P 1 V 1 = P 2 V 2 T 1 T 2 (702. 5 torr)(25. 0 m. L) = (760 torr)(V 2) 298 K 273 K VN 2 = 21. 2 m. L

Try These! 1. Gas samples A, B, and C are contained in a system at STP. The partial pressure of sample A is 50. 5 k. Pa and the partial pressure of sample B is 22. 8 k. Pa. What is the partial pressure of sample C?

2. When 10. 00 moles of gas A and 5. 00 moles of gas B are combined, the total pressure exerted by the gas mixture is 98. 0 k. Pa. What is the partial pressure exerted by gas A in the mixture?

3. A 32. 0 m. L sample of hydrogen is collected over water at 30°C and 750. 0 torr pressure. What is the volume of the dry gas at STP? (Vapor pressure of water at 30°C = 31. 9 torr)