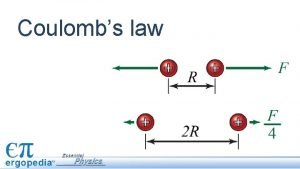
Coulombs Law Gausss Law Coulombs Law Discussion 1

Coulomb´s Law & Gauss´s Law Coulomb´s Law Discussion : 1. Experimental Law 2. Applicable to point charges only 3. Gives Force between charges at rest and not for Charges in motion 4. Coulomb interaction between charges is a long range force 5. Follows Newton’s third Law 6. Gives Force between charges at rest and not for charges in motion 7. Coulomb interaction is long range force

Physics Paper C BSc I
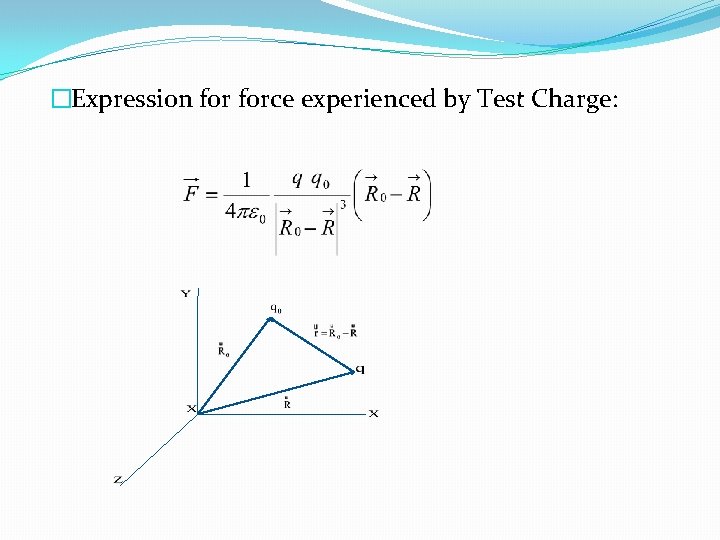
�Expression force experienced by Test Charge:

Important Definitions �Source Charge : A point charge which exerts electrostatic force and produces an electric field. �Test Charge: A point charge which experiences electrostatic force and detectes an electric field. �Source point: Location of source charge. �Test point/ Observation point : Location of test charge.

Electric Field � The space around a charged body within which its influence can be felt/ The space around a charged body within which it exerts force on a test charge. � Electric Field Intensity: Electric Field Intensity at a point is force experienced per unit test charge at that point. � Unit: NC-1 or Vm-1 � Vector Quantity

Principle of Superposition of Electric Fields �The electric field at any point due to a set of fixed charges is equal to the vector sum of electric fields due to individual charges. �For discrete distribution of charge

• For linear distribution of charge • For surface distribution of charge • For volume distribution of charge

Electric Dipole �A system consisting of two equal and opposite charges (–q and +q) separated by certain distance (2 l) � Electric dipole moment p -q 2 l +q Directed from negative to positive charge. � Monopole moment of electric dipole : Algebraic sum of charges and is equal to zero.
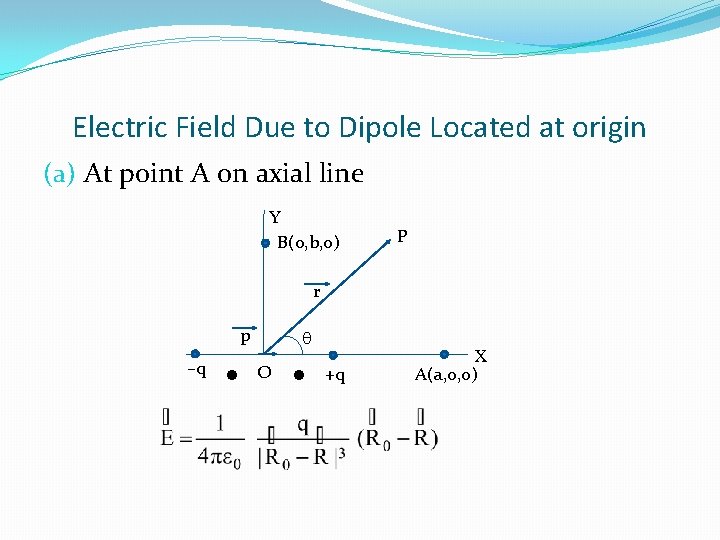
Electric Field Due to Dipole Located at origin (a) At point A on axial line Y B(0, b, 0) P r p –q l q O l +q X A(a, 0, 0)


(b) At a point on equatorial line

(c) At arbitrary point Y P r p –q l q O l +q X

Electric Field due to Infinite Linear Distribution of Y Charge L(0, y, 0) q R 0 R – 0 (x, 0, 0) X ldx +

Electric Field Due to z. Uniformly Charged Ring R dq ldl q O x P(x, 0, 0) y

Electric Field due to Uniformly Charged Circular Disc z a r O x dr y P(x, 0, 0) If =surface charge density Electric field at P(x, 0, 0) due to elementary ring


Electric Flux �The electric flux linked with an area is the number of electric force field lines crossing that area. �For uniform electric field �For non uniform electric field �Electric Flux may be + ve or – ve or zero �Outward Flux is + ve , Inward Flux is -ve

Gauss’s Law �The total electric flux through a closed surface is equal to times the charge enclosed by the surface when medium is vacuum. � If the closed surface encloses a no. of charges Where qnet is the net charge enclosed by the surface.

Differential form of Gauss’s Law • • It relates the electric field at any point in space to the volume charge density ρ at same point. It is a point equation. It is one of the Maxwell’s equations for electricity and magnetism. It can be used to find volume charge density at a given point if electric field intensity at that point is known.
- Slides: 19