Last Lecture Gausss law Using Gausss law for





- Slides: 16

Last Lecture Gauss’s law Using Gauss’s law for: spherical symmetry This lecture Using Gauss’s law for: line symmetry plane symmetry Conductors in electric fields

Coulomb’s law tutorial: Consider two positively charged particles, one of charge q 0 (particle 0) fixed at the origin, and another of charge q 1 (particle 1) fixed on the y-axis at (0, d 1, 0). What is the net force F on particle 0 due to particle 1? Express your answer (a vector) using any or all of k, q 0, q 1, d 1, x-hat, y-hat, and z-hat. Example of wrong answer: ( Answer: F = )

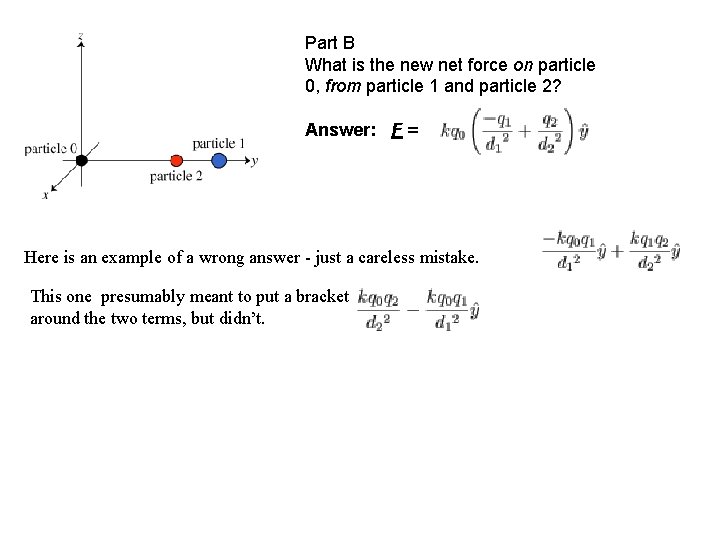
Part B What is the new net force on particle 0, from particle 1 and particle 2? Answer: F = Here is an example of a wrong answer - just a careless mistake. This one presumably meant to put a bracket around the two terms, but didn’t.

Part D What is the net force on particle 0 due solely to this charge 3? Answer: F = The answer here was close but still missing a factor of ½. The message is that accuracy matters.

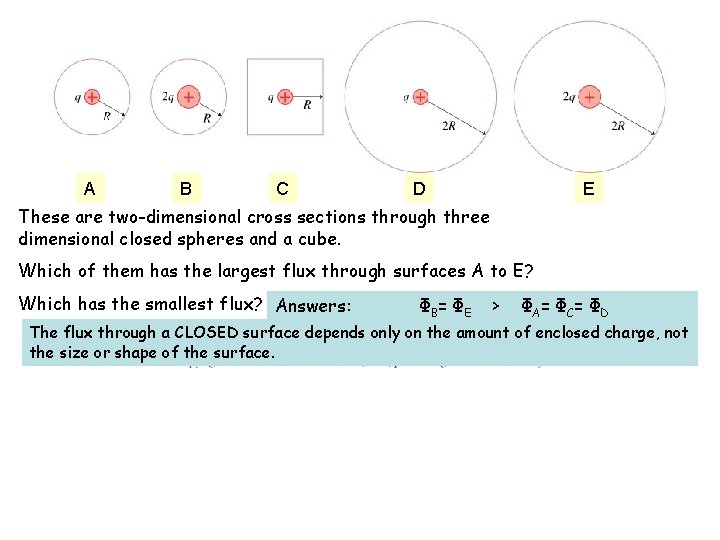
A B C D E These are two-dimensional cross sections through three dimensional closed spheres and a cube. Which of them has the largest flux through surfaces A to E? Which has the smallest flux? Answers: ΦB = ΦE > ΦA= ΦC= ΦD The flux through a CLOSED surface depends only on the amount of enclosed charge, not the size or shape of the surface.

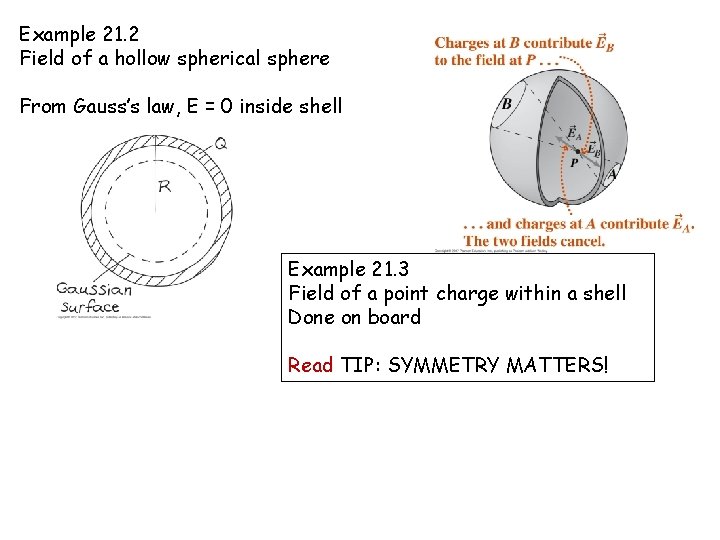
Example 21. 2 Field of a hollow spherical sphere From Gauss’s law, E = 0 inside shell Example 21. 3 Field of a point charge within a shell Done on board Read TIP: SYMMETRY MATTERS!

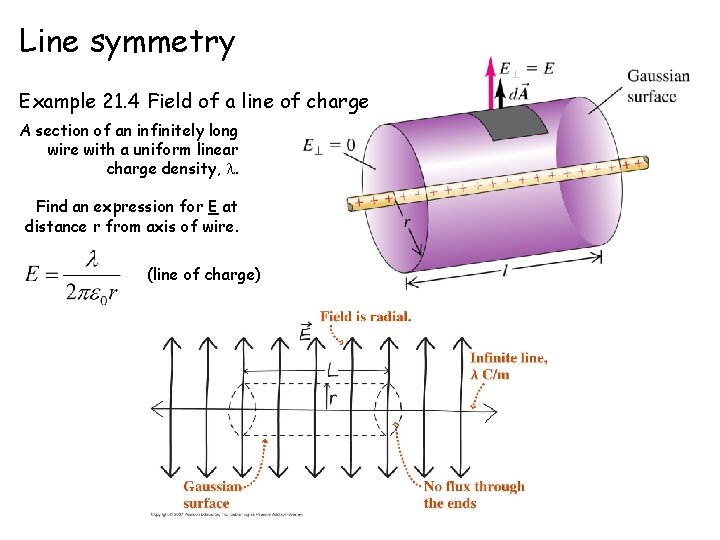
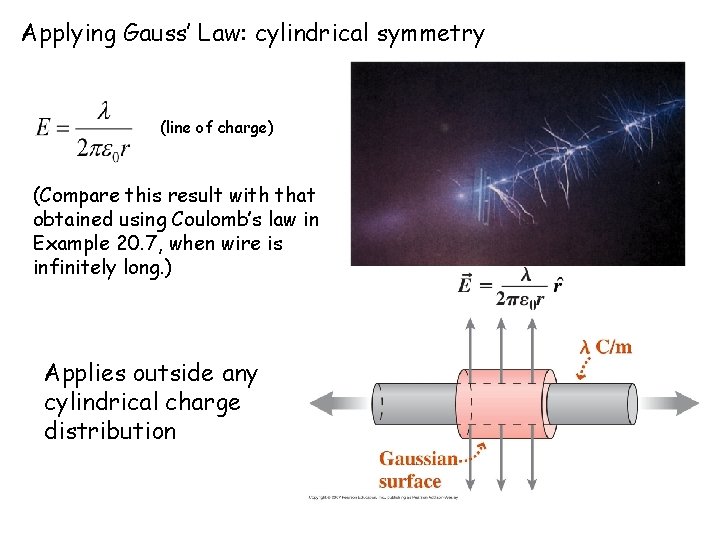
Line symmetry Example 21. 4 Field of a line of charge A section of an infinitely long wire with a uniform linear charge density, . Find an expression for E at distance r from axis of wire. (line of charge)

Applying Gauss’ Law: cylindrical symmetry (line of charge) (Compare this result with that obtained using Coulomb’s law in Example 20. 7, when wire is infinitely long. ) Applies outside any cylindrical charge distribution

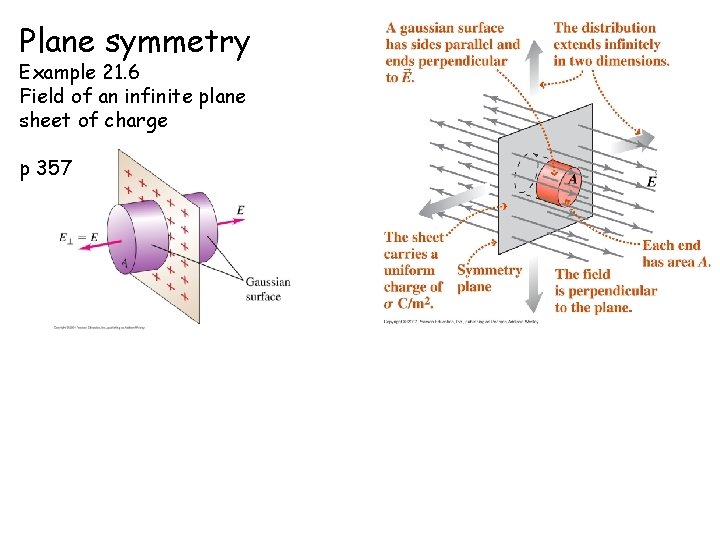
Plane symmetry Example 21. 6 Field of an infinite plane sheet of charge p 357

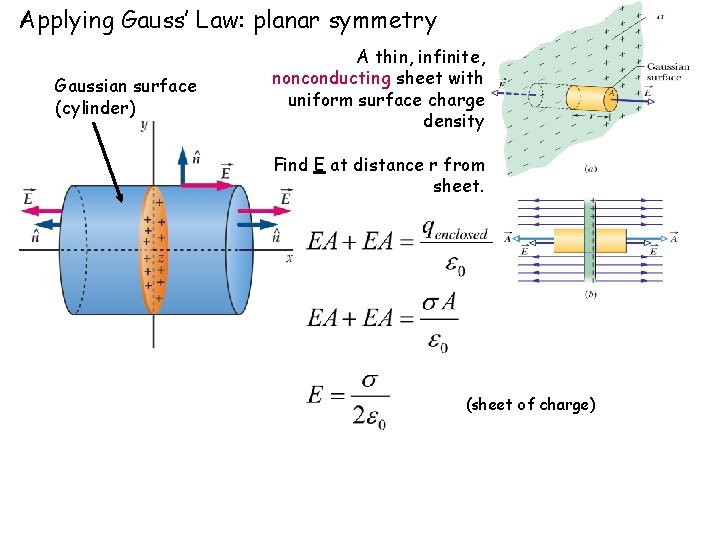
Applying Gauss’ Law: planar symmetry Gaussian surface (cylinder) A thin, infinite, nonconducting sheet with uniform surface charge density Find E at distance r from sheet. (sheet of charge)

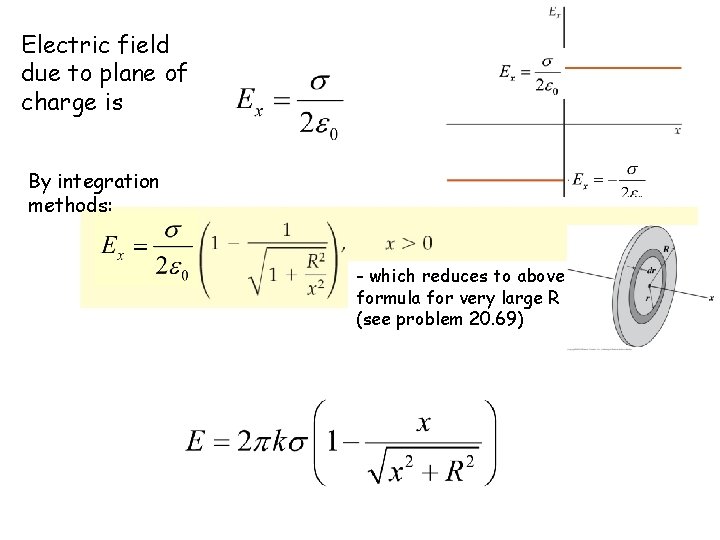
Electric field due to plane of charge is By integration methods: - which reduces to above formula for very large R (see problem 20. 69)

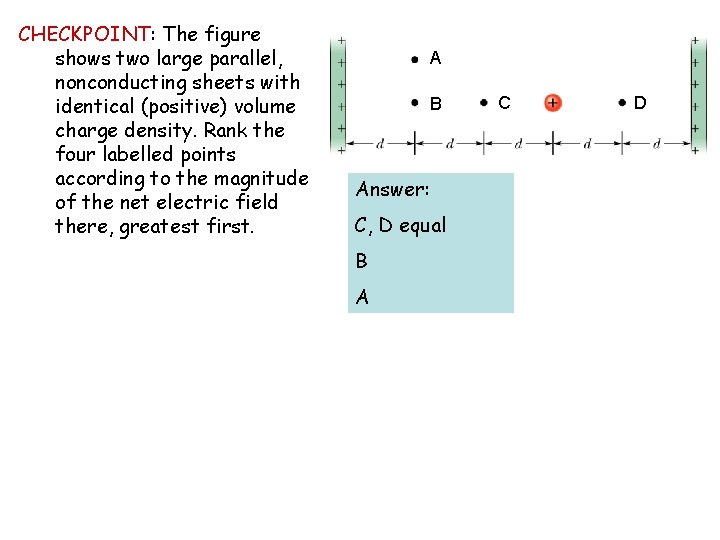
CHECKPOINT: The figure shows two large parallel, nonconducting sheets with identical (positive) volume charge density. Rank the four labelled points according to the magnitude of the net electric field there, greatest first. A B Answer: C, D equal B A C D

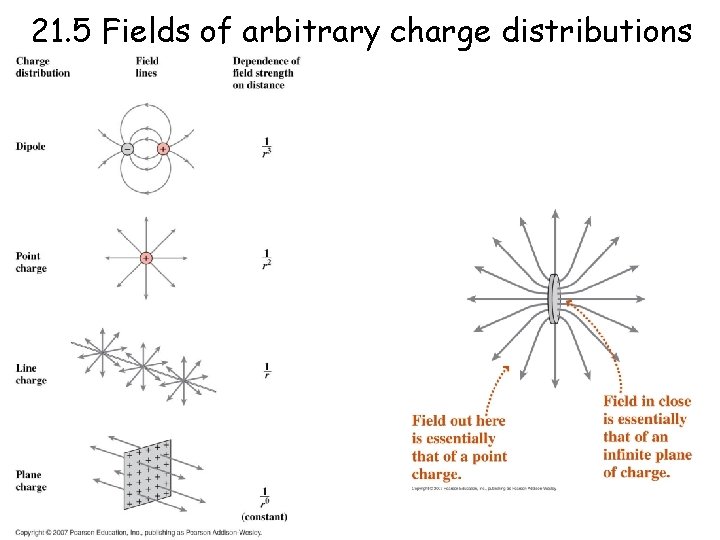
21. 5 Fields of arbitrary charge distributions

CHECKPOINT: There is a certain net flux I through a Gaussian sphere of radius r enclosing an isolated charged particle. Suppose the Gaussian surface is changed to (a) a larger Gaussian sphere, (b) a Gaussian cube with edge length equal to r, and (c) a Gaussian cube with edge length 2 r. In each case is the net flux through the new Gaussian surface A. greater than Answers: all equal as B. less than, or charge enclosed is C. equal to I ? the same

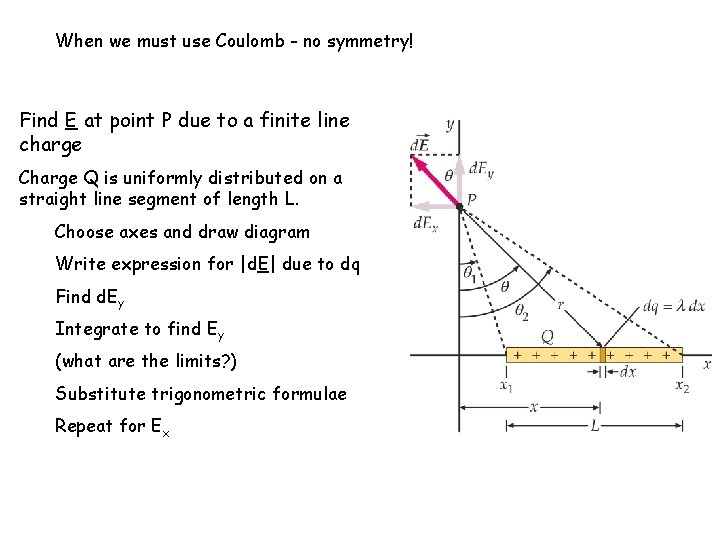
When we must use Coulomb - no symmetry! Find E at point P due to a finite line charge Charge Q is uniformly distributed on a straight line segment of length L. Choose axes and draw diagram Write expression for |d. E| due to dq Find d. Ey Integrate to find Ey (what are the limits? ) Substitute trigonometric formulae Repeat for Ex

True A or False? False F 1. If the net electric flux out of a closed surface is zero, the electric False field must be zero everywhere on the surface. 2. If the net electric flux out of a closed surface is zero, the charge False density must be zero everywhere inside the surface. 3. The electric field is zero everywhere within the material of a conductor in electrostatic equilibrium. 4. The tangential component of the electric field is zero at all points just outside the surface of a conductor in electrostatic equilibrium. True 5. True The normal component of the electric field is the same at all points False just outside the surface of a conductor in electrostatic equilibrium.