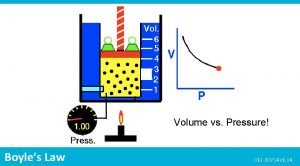
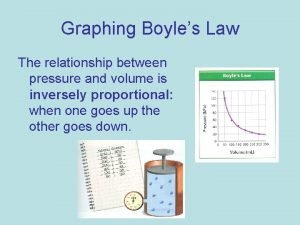
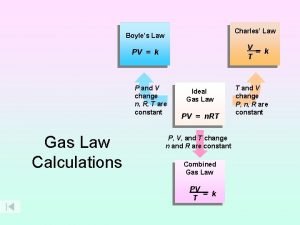
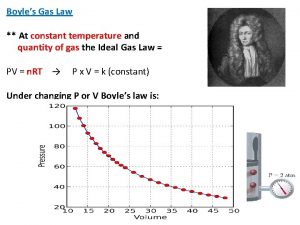
Boyles law PV constant k V 1 Charless

Boyle's law PV = constant (k) V 1 Charles's law = T 1 Avogadro’s law P 1 V 1 = P 2 V 2 T 2 V=kn Ideal gas equation d = PM RT PV = n. RT M = d. RT P Combined gas law P 2 V 2 P 1 V 1 = T 2 T 1 RT RT n Pt=(n 1+n 2+n 3…. ) = t V V ( (

Example: Calcium carbonate, Ca. CO 3(s), decomposes upon heating to give Ca. O(s) and CO 2(g). A sample of Ca. CO 3 is decomposed, and the carbon dioxide is collected in a 250 -m. L flask. After the decomposition is complete, the gas has a pressure of 1. 3 atm at a temperature of 31 °C. How many moles of CO 2 gas were generated? PV = n. RT

Example: The gas pressure in an aerosol can is 1. 5 atm at 25 °C. Assuming that the gas inside obeys the ideal-gas equation, what would the pressure be if the can were heated to 450 °C? PV = n. RT

Example: A large natural-gas storage tank is arranged so that the pressure is maintained at 2. 20 atm. On a cold day in December when the temperature is – 15 °C (4 °F), the volume of gas in the tank is 3. 25 × 103 m 3. What is the volume of the same quantity of gas on a warm July day when the temperature is 31 °C (88 °F)? P 1= 2. 20 atm V 1 = 3. 25 x 103 m 3 T 1= -15 o. C = -15+273 = 258 K P 2 = 2. 20 atm V 2 = ? T 2= -15 o. C = 31+273 = 304 K Answer: 3. 83 × 103 m 3 P 2 V 2 P 1 V 1 = T 2 T 1 V 2 V 1 = T 2 T 1

Partial Pressures • When one collects a gas over water, there is water vapor mixed in with the gas. • To find only the pressure of the desired gas, one must subtract the vapor pressure of water from the total pressure.

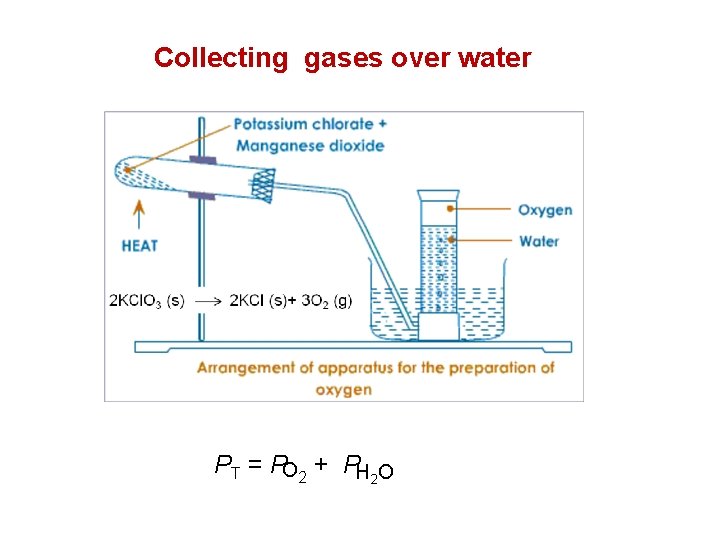
Collecting gases over water PT = PO 2 + PH 2 O

Example 2: Oxygen gas generated by the decomposition of potassium chlorate is collected over water. The volume of oxygen collected at 24 C and atmospheric pressure of 762 mm. Hg is 128 m. L. Calculate the mass (in grams) of oxygen gas obtained. The pressure of the water vapor at 24 C is 22. 4 mm. Hg. PT = PO 2 + PH 2 O P O 2 = P T - PH O = 762 mm. Hg – 22. 4 mm. Hg 2 =739. 6 mm. Hg = 739. 6 mm. Hg P = 0. 973 atm T = 273 + 24 = 297 K number of mole, n = V = 128 m. L = 0. 128 L M = molar mass = 32 g / mol R = 0. 08206 L. atm /K. mol m =mass in gram ? PV = n. RT = m= 1 atm = 0. 973 atm 760 mm. Hg m RT M PVM 0. 973 atm 0. 128 L 32 g / mol = 0. 163 g = RT 0. 0821 L. atm / K. mol 297 K m M

10. 7 Kinetic-molecular theory The kinetic-molecular theory is summarized by the following statements: 1. Gases consist of large numbers of molecules that are in continuous, random motion 2. The combined volume of all the molecules of the gas is negligible relative to the total volume in which the gas is contained 3. Attractive and repulsive forces between gas molecules are negligible 4. Energy can be transferred between molecules during collisions, but the average kinetic energy of the molecules does not change with time 5. The average kinetic energy of the molecules is proportional to the absolute temperature

Distribution of molecular speed Average kinetic energy of a gas molecules: = 12 mu 2 u, root-mean-square (rms) m, mass of individual molecule rms and average speed : If we have four objects with speeds of 4. 0, 6. 0, 10. 0 and 12. 0 m/s = ( ( 4. 02 + 6. 02 + 10. 02 + 12. 02 4 ( rms speed = 4. 0 + 6. 0 + 10. 0 + 12. 0 = 8 m/s 4 ( Average speed = The effect of temperature on molecular speeds 16 + 36 + 100+ 144 4 = 74 = 8. 6 m/s

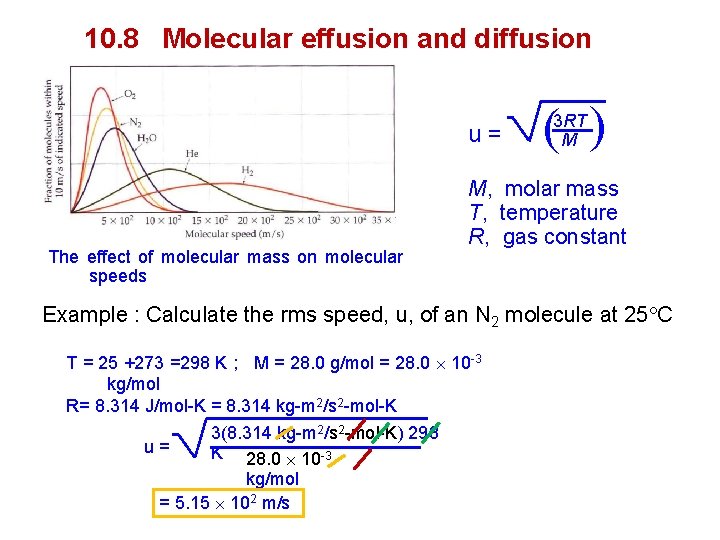
10. 8 Molecular effusion and diffusion The effect of molecular mass on molecular speeds ( ( u= 3 RT M M, molar mass T, temperature R, gas constant Example : Calculate the rms speed, u, of an N 2 molecule at 25 C T = 25 +273 =298 K ; M = 28. 0 g/mol = 28. 0 10 -3 kg/mol R= 8. 314 J/mol-K = 8. 314 kg-m 2/s 2 -mol-K 3(8. 314 kg-m 2/s 2 -mol-K) 298 u= K 28. 0 10 -3 kg/mol = 5. 15 102 m/s

The dependence of molecular speeds on mass has two consequences: 1. Effusion : escape of gas molecule through a tiny hole into an evacuated space Gas molecule effuse through a pinhole in the partitioning wall only when they happen to hit the hole 2. Diffusion : spread of one substance through a space or throughout a second substance Each short segment of line represents travel between collisions. The blue arrow indicates the net distance traveled by the molecule

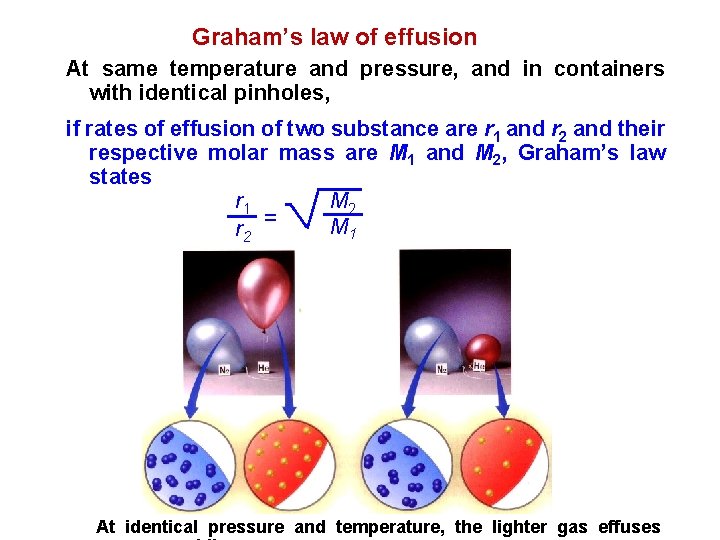
Graham’s law of effusion At same temperature and pressure, and in containers with identical pinholes, if rates of effusion of two substance are r 1 and r 2 and their respective molar mass are M 1 and M 2, Graham’s law states M 2 r 1 M 1 r 2 = At identical pressure and temperature, the lighter gas effuses

r. N 2 Example : Calculate the ratio of the effusion rates of N 2 and O 2, r. O 2 M N 2= 28 g/mol M O 2= 32 g/mol r. N 2 r. O 2 = = MO 2 M N 2 32 28 r. N 2 r. O 2 = 1. 07

10. 9 Real gases : Deviations from ideal behavior For a gas to exhibit idea behavior two assumptions are considered: 1. Intermolecular forces: The attractions and repulsions between the particles are negligible (i. e. , small or non existent intermolecular forces) 2. Negligible volume: A gas is made up of a large number of particles (atoms or molecules) whose size is negligible compared to the size of the container. These particles are also small compared to the distances between particles. Real molecules, however, do have finite volumes and they do attract one another

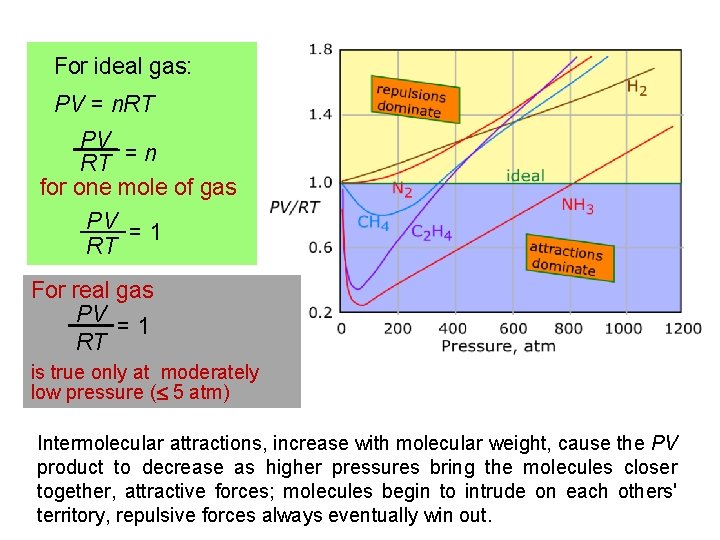
For ideal gas: PV = n. RT PV RT = n for one mole of gas PV = 1 RT For real gas PV = 1 RT is true only at moderately low pressure ( 5 atm) Intermolecular attractions, increase with molecular weight, cause the PV product to decrease as higher pressures bring the molecules closer together, attractive forces; molecules begin to intrude on each others' territory, repulsive forces always eventually win out.

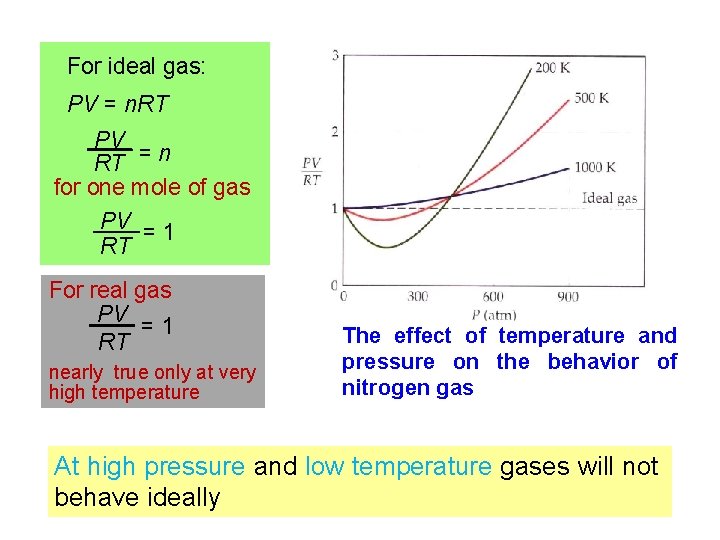
For ideal gas: PV = n. RT PV RT = n for one mole of gas PV = 1 RT For real gas PV =1 RT nearly true only at very high temperature The effect of temperature and pressure on the behavior of nitrogen gas At high pressure and low temperature gases will not behave ideally

The Van der Waals equation The two factor leading to deviations from ideal behavior 1. molecular attractions 2. molecular volume Van der Waal’s suggested correction for real gas : Pressure correction : Volume correction : Pideal = Preal 2 an + 2 V Videal = (Vreal – nb) “a” is a correction for intermolecular forces “nb” represents volume occupied by n moles of the gas Taking into account the corrections for pressure and volume: an 2 P + V 2 V – nb = n. RT Van der Waals equation a and b are van der Waals constants and different for different

Example : If a sample of 1. 00 mol of CO 2(g) is confined to a volume of 3. 00 L at 0. 0 C, calculate the pressure of the gas using (a) the idealgas equation and (b) the van der Waals equation. [For CO 2(g) a = 3. 59 atm. L 2/mol 2 and b = 0. 0427 L/mol] n = 1. 00 mol V = 3. 00 L T = 0 +273 = 273 K R = 0. 0821 L. atm/K. mol (a) For ideal gas : P= 1 mol 0. 0821 L. atm/K. mol 273 K n. RT = = 7. 471 atm V 3. 00 L 2 n. RT an (b) For real gas : P + = V -nb V 2 3. 59 atm. L 2/mol 2 (1 mol)2 an 2 = 2 V (3. 00 L)2 = 0. 399 atm V – nb = 3. 00 L – (1 mol 0. 0427 L/mol) = 2. 957 L 1. 0 mol 0. 0821 L. atm/K. mol 273 K P + 0. 399 atm = 2. 957 L P + 0. 399 atm = 7. 580 atm P = 7. 181 atm