4 Gausss law 4 1 Electric flux Uniform




- Slides: 12

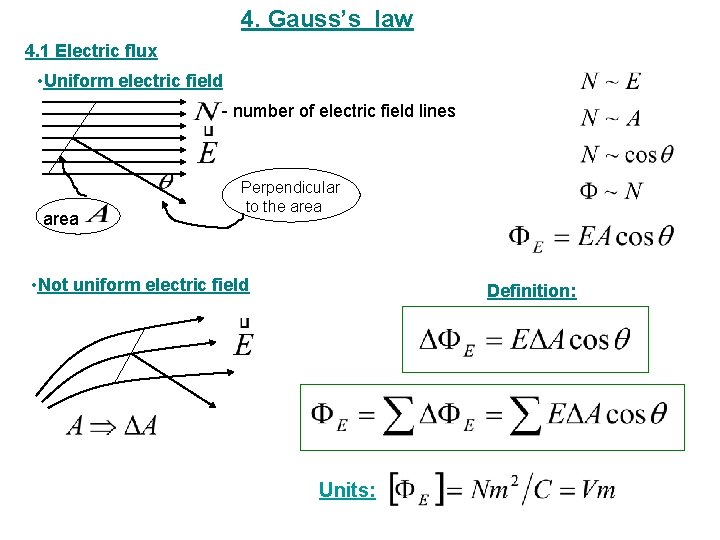
4. Gauss’s law 4. 1 Electric flux • Uniform electric field - number of electric field lines area Perpendicular to the area • Not uniform electric field Definition: Units:

Example: Flux through open surface Compare the electric flux through two squares of areas A 1 and A 2 (A 2>A 1) placed in a region with a uniform electric field E: (Side view) A 2 A. Φ 1 < Φ 2 θ θ A 1 A 2 cosθ E B. Φ 1 = Φ 2 C. Φ 1 > Φ 2 A 2 The number of lines going through them is the same. The effective area for the large square is A 2 cosθ = A 1 • If you reverse the direction of A, you reverse the sign of the flux • For an open surface, choose any direction • For a closed surface it is conventional to take the area vector pointing outwards Ф > 0 lines going out Ф < 0 lines coming in Ф = 0 no lines or a balance between incoming and outgoing lines

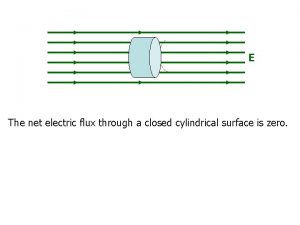
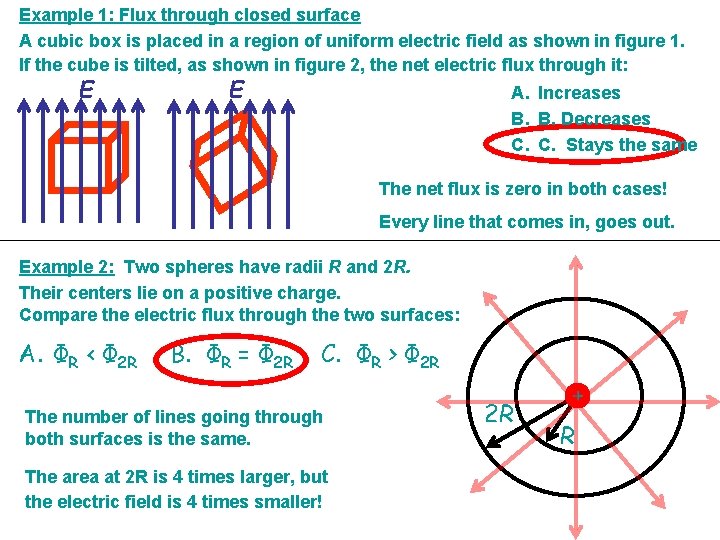
Example 1: Flux through closed surface A cubic box is placed in a region of uniform electric field as shown in figure 1. If the cube is tilted, as shown in figure 2, the net electric flux through it: E E A. Increases B. B. Decreases C. C. Stays the same The net flux is zero in both cases! Every line that comes in, goes out. Example 2: Two spheres have radii R and 2 R. Their centers lie on a positive charge. Compare the electric flux through the two surfaces: A. ΦR < Φ 2 R B. ΦR = Φ 2 R C. ΦR > Φ 2 R The number of lines going through both surfaces is the same. The area at 2 R is 4 times larger, but the electric field is 4 times smaller! 2 R + R

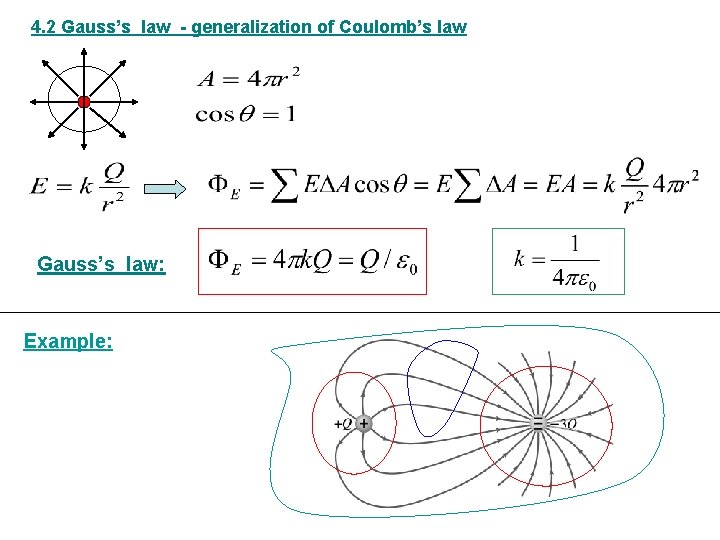
4. 2 Gauss’s law - generalization of Coulomb’s law Gauss’s law: Example:

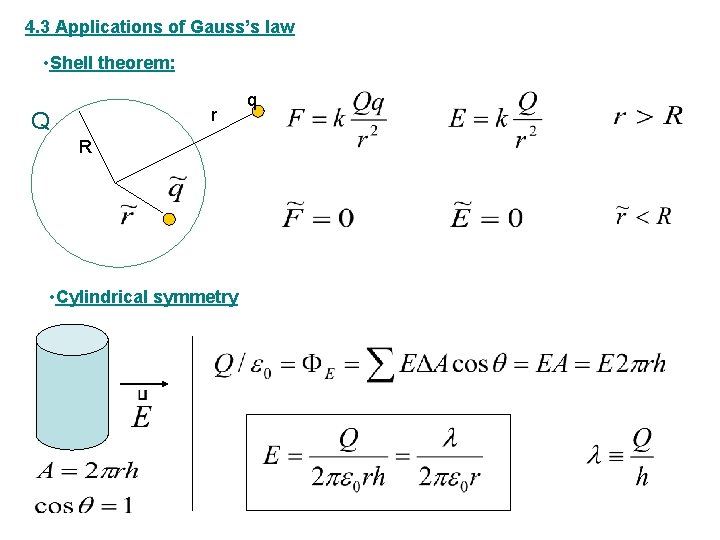
4. 3 Applications of Gauss’s law • Shell theorem: r Q R • Cylindrical symmetry q

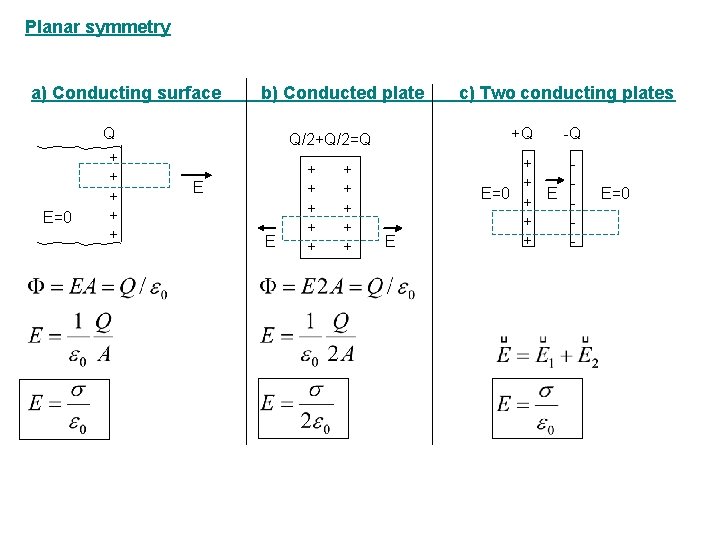
Examples (applications of Gauss’s law): Electric field created by Point charge, charged sphere or spherical shell (Spherical symmetry) Long cylinder or tube (Cylindrical symmetry) Conducting plane surface, and two conducting parallel plates (Planar symmetry) One conducting plate (Planar symmetry)

Planar symmetry a) Conducting surface b) Conducted plate Q E=0 + + +Q Q/2+Q/2=Q E E + + + + + c) Two conducting plates E -Q + + E=0 E + + + - E=0

Example: A solid metal sphere of radius 3. 00 m carries a total charge of 3. 5μC. What is the magnitude of the electric field at a distance from the sphere’s center of (a) 0. 15 m, (b) 2. 90 m, (c) 3. 10 m, and (d) 6. 00 m? (e) How would the answers differ if the sphere were a thin shell? (a) and (b) Inside a solid metal sphere the electric field is 0 (c) Outside a solid metal sphere the electric field is the same as if all the charge were concentrated at the center as a point charge: (d) Same reasoning as in part (c): (e) The answers would be no different for a thin metal shell

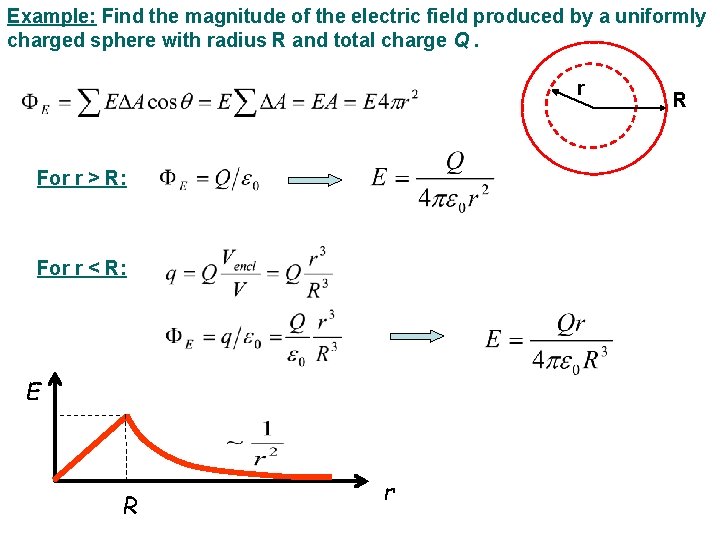
Example: Find the magnitude of the electric field produced by a uniformly charged sphere with radius R and total charge Q. r For r > R: For r < R: E R r R

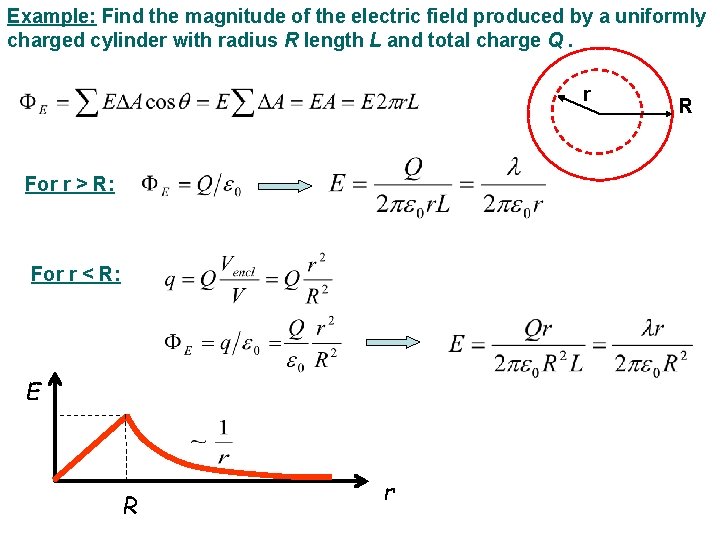
Example: Find the magnitude of the electric field produced by a uniformly charged cylinder with radius R length L and total charge Q. r For r > R: For r < R: E R r R

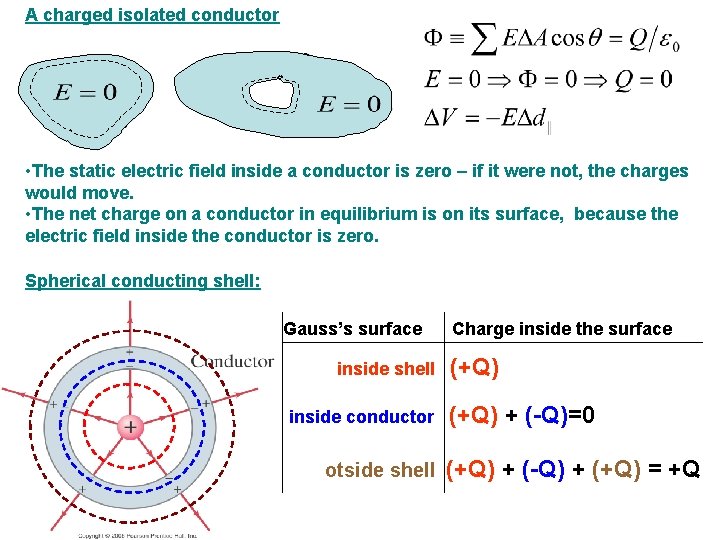
A charged isolated conductor • The static electric field inside a conductor is zero – if it were not, the charges would move. • The net charge on a conductor in equilibrium is on its surface, because the electric field inside the conductor is zero. Spherical conducting shell: Gauss’s surface inside shell inside conductor otside shell Charge inside the surface (+Q) + (-Q)=0 (+Q) + (-Q) + (+Q) = +Q

Example: Compare the magnitude of the electric field at point P before and after the shell is removed. Hint: Use Gauss’s law to find EP. A. Ebefore < Eafter B. Ebefore = Eafter σin σout C. Ebefore > Eafter In both cases, the symmetry is the same. We will use the same Gaussian surface: a sphere that contains point P. So the flux will look just the same: And the enclosed charge is also the same: Q. Therefore, Q P