DIFFERENTIATION Outcome 3 Using differentiation Application Finding the





































































- Slides: 93

DIFFERENTIATION Outcome 3 Using differentiation (Application) Finding the gradient for a polynomial Increasing / Decreasing functions Differentiating Brackets ( Type 1 ) Max / Min and inflexion Points Differentiating Harder Terms (Type 2) Curve Sketching Differentiating with Leibniz Notation Max & Min Values on closed Intervals Equation of a Tangent Line ( Type 3 ) Optimization Mind Map of Chapter

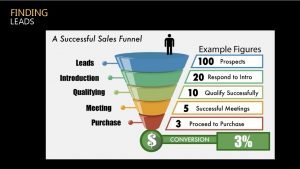
Gradients & Curves Outcome 3 Higher On a straight line the gradient remains constant, however with curves the gradient changes continually, and the gradient at any point is in fact the same as the gradient of the tangent at that point. S B The sides of the half-pipe are very steep(S) but it is not very steep near the base(B). Demo

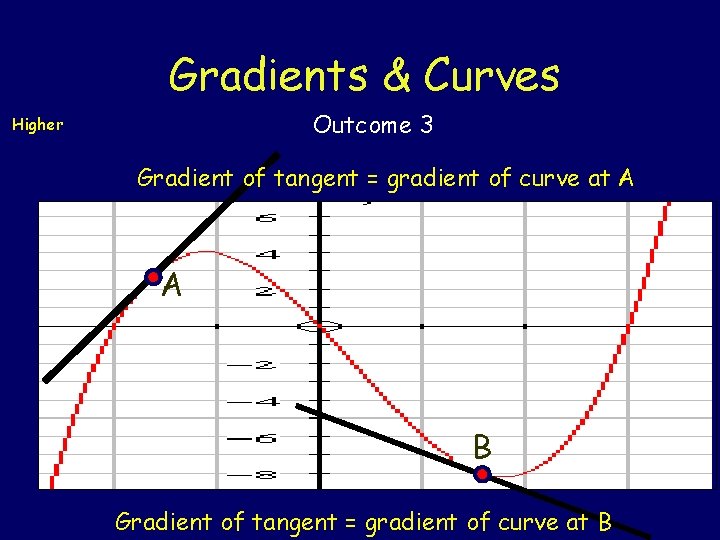
Gradients & Curves Outcome 3 Higher Gradient of tangent = gradient of curve at A A B Gradient of tangent = gradient of curve at B

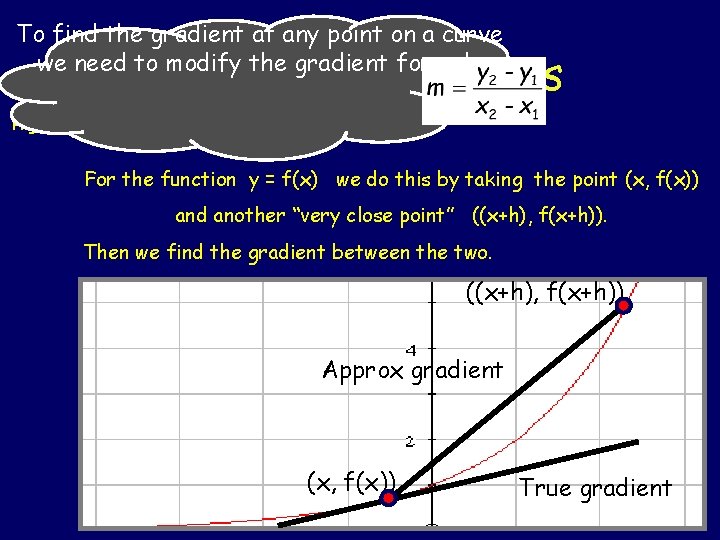
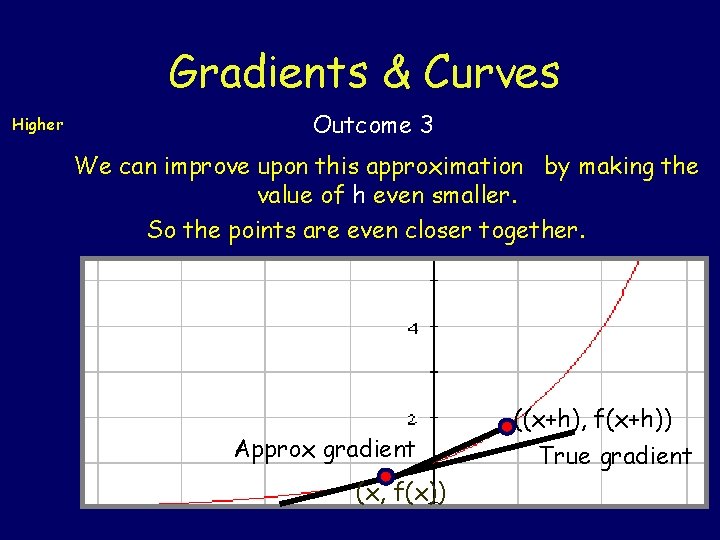
To find the gradient at any point on a curve we need to modify the gradient formula Gradients & Curves Higher Outcome 3 For the function y = f(x) we do this by taking the point (x, f(x)) and another “very close point” ((x+h), f(x+h)). Then we find the gradient between the two. ((x+h), f(x+h)) Approx gradient (x, f(x)) True gradient

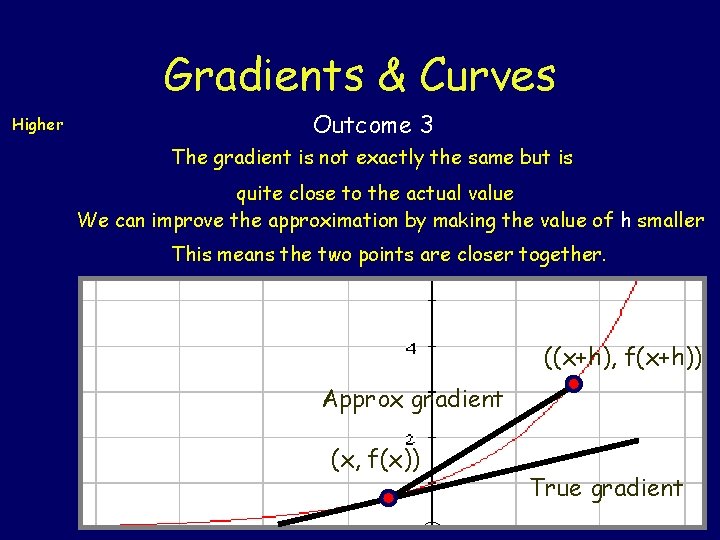
Gradients & Curves Higher Outcome 3 The gradient is not exactly the same but is quite close to the actual value We can improve the approximation by making the value of h smaller This means the two points are closer together. ((x+h), f(x+h)) Approx gradient (x, f(x)) True gradient

Gradients & Curves Higher Outcome 3 We can improve upon this approximation by making the value of h even smaller. So the points are even closer together. Approx gradient (x, f(x)) ((x+h), f(x+h)) True gradient

Derivative Higher Outcome 3 We have seen that on curves the gradient changes continually and is dependant on the position on the Finding the curve. ie the x-value of the given point. GRADIENT Differentiating The process of finding the gradient is called Finding the rate of DIFFERENTIATING change or FINDING THE DERIVATIVE (Gradient)

Derivative Outcome 3 Higher If the formula/equation of the curve is given by f(x) Then the derivative is called f '(x) - “f dash x” f(x) f '(x) There is a simple way 2 x 2 4 x 2 5 x 10 6 x 7 x 3 x 5 x 99 4 x 8 x 50 x 9 42 x 6 3 x 2 5 x 4 99 x 98 of finding f '(x) from f(x). Have guessed the rule yet !

Derivative Higher Rule for Differentiating Outcome 3 It can be given by this simple flow diagram. . . multiply by the power If reduce the power by 1 f(x) then f '(x) = axn n 1 = ax NB: the following terms & expressions mean the same GRADIENT, DERIVATIVE, RATE OF CHANGE, f '(x)

Derivative Higher Rule for Differentiating Outcome 3 To be able to differentiate it is VERY IMPORTANT that you are comfortable using indices rules

Special Points Outcome 3 Higher (I) f(x) = ax (Straight line function) If f(x) = ax = Index Laws ax 1 then f '(x) = 1 X ax 0 = 1 = a. X 1 = a So if g(x) = 12 x then Also using g '(x) = 12 y = mx + c The line y = 12 x has gradient 12, and derivative = gradient !!

Special Points Outcome 3 Higher (II) f(x) = a, (Horizontal Line) If f(x) = a X 1 = ax 0 then f '(x) = 0 X ax-1 So if g(x) = -2 then Also using formula Index Laws x 0 = 1 = 0 g '(x) = 0 y = c , (see outcome 1 !) The line y = -2 is horizontal so has gradient 0 !

ion t a i nt e i r = e d f Gra Dif Name : Differentiation techniques ge ion n t a a i ch = f ent r o e e f Rat Dif

Calculus Revision Differentiate

Calculus Revision Differentiate

Calculus Revision Differentiate

Derivative Outcome 3 Higher Example 1 A curve has equation f(x) = 3 x 4 Find the formula for its gradient and find the gradient when x = 2 Its gradient is f '(x) = 12 x 3 f '(2) = 12 X 23 = Example 2 12 X 8 = 96 A curve has equation f(x) = 3 x 2 Find the formula for its gradient and find the gradient when x = -4 Its gradient is f '(x) = 6 x At the point where x = -4 the gradient is f '(-4) = 6 X -4 = -24

Derivative Outcome 3 Higher Example 3 If g(x) = 5 x 4 - 4 x 5 then find g '(2). g '(x) = 20 x 3 - 20 x 4 g '(2) = 20 X 23 - 20 X 24 = 160 - 320 = -160

Derivative Outcome 3 Higher Example 4 h(x) = 5 x 2 - 3 x + 19 and so h '(-4) = 10 X (-4) - 3 h '(x) = 10 x - 3 = -40 - 3 = -43 Example 5 k(x) = 5 x 4 - 2 x 3 + 19 x - 8, find k '(10). k '(x) = 20 x 3 - 6 x 2 + 19 So k '(10) = 20 X 1000 - 6 X 100 + 19 = 19419

Derivative Outcome 3 Higher Example 6 : Find the points on the curve f(x) = x 3 - 3 x 2 + 2 x + 7 where the gradient is 2. NB: gradient = derivative = f '(x) We need ie f '(x) = 2 3 x 2 - 6 x + 2 = 2 or 3 x 2 - 6 x = 0 ie 3 x(x - 2) = 0 ie so 3 x = 0 or x-2=0 x = 0 or x = 2 Now using original formula f(0) = 7 f(2) = 8 -12 + 4 + 7 =7 Points are (0, 7) & (2, 7)

Calculus Revision Differentiate

Calculus Revision Differentiate Straight line form Differentiate

Calculus Revision Differentiate Straight line form Differentiate

Calculus Revision Differentiate Straight line form Chain Rule Simplify

Calculus Revision Differentiate Straight line form Differentiate

Calculus Revision Differentiate Straight line form Differentiate

Calculus Revision Differentiate Straight line form Differentiate

Brackets Outcome 3 Higher Basic Rule: Break brackets before you differentiate ! Example h(x) = 2 x(x + 3)(x -3) = 2 x(x 2 - 9) = 2 x 3 - 18 x So h'(x) = 6 x 2 -18

Calculus Revision Differentiate Multiply out Differentiate

Calculus Revision Differentiate multiply out differentiate

Calculus Revision Differentiate Straight line form multiply out Differentiate

Calculus Revision Differentiate multiply out Differentiate

Calculus Revision Differentiate multiply out Simplify Straight line form Differentiate

Calculus Revision Differentiate Multiply out Straight line form Differentiate

Fractions Higher Outcome 3 Reversing the above we get the following “rule” ! This can be used as follows …. .

Fractions Outcome 3 Higher Example f(x) = 3 x 3 - x + 2 x 2 x 2 = 3 x - x-1 + 2 x-2 f '(x) = 3 + x-2 - 4 x-3 = 3 + 1 - 4 x 2 x 3

Calculus Revision Differentiate Split up Straight line form Differentiate

Leibniz Notation Outcome 3 Higher Leibniz Notation is an alternative way of expressing derivatives to f'(x) , g'(x) , etc. If y is expressed in terms of x then the derivative is written as dy/dx. eg y = 3 x 2 - 7 x Example 19 dy/ dx = 6 x - 7. Q = 9 R 2 - 15 R 3 NB: So so Find d. Q/ d. R Q = 9 R 2 - 15 R-3 d. Q/ d. R = 18 R + 45 R-4 = 18 R + 45 R 4

Leibniz Notation Outcome 3 Higher Example 20 A curve has equation y = 5 x 3 - 4 x 2 + 7. Find the gradient where x = -2 ( differentiate ! ) gradient = dy/ dx = 15 x 2 - 8 x if x = -2 then gradient = 15 X (-2)2 - 8 X (-2) = 60 - (-16) = 76

Real Life Example Physics Outcome 3 Higher Newton’s 2 nd. Law of Motion s = ut + 1/2 at 2 Finding ds/ where s = distance & t = time. means “diff in dist” dt ie so but ds/ dt dt and this is “diff in time” speed or velocity = u + at = v so we get v = u + at Newton’s 1 st Law of Motion

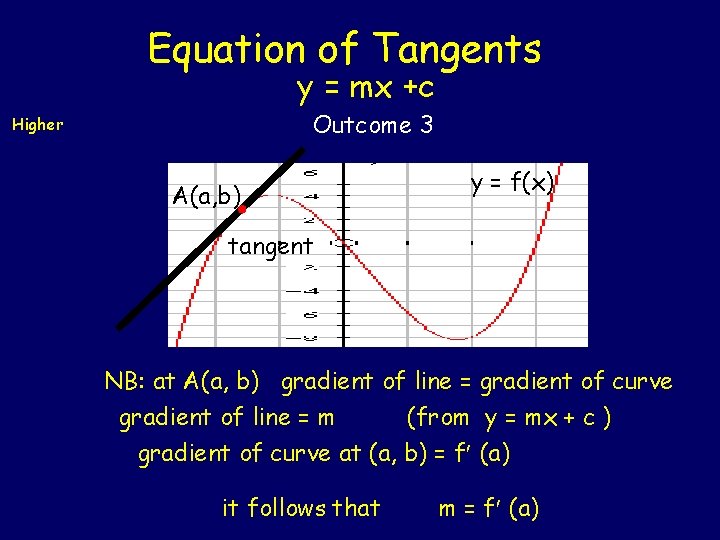
Equation of Tangents y = mx +c Outcome 3 Higher A(a, b) y = f(x) tangent NB: at A(a, b) gradient of line = gradient of curve gradient of line = m (from y = mx + c ) gradient of curve at (a, b) = f (a) it follows that m = f (a)

Straight line so need a point Equation ofwe. Tangents Higher plus the gradient then we can use the formula y - b = m(x - a). Outcome 3 Example 21 Find the equation of the tangent line to the curve y = x 3 - 2 x + 1 at the point where x = -1. Point: if x = -1 then y = (-1)3 - (2 X -1) + 1 = -1 - (-2) + 1 = 2 Gradient: when x = -1 dy/ dx point is (-1, 2) = 3 x 2 - 2 = 3 X (-1)2 - 2 = 3 -2 = 1 m=1

Equation of Tangents Outcome 3 Higher Now using y - b = m(x - a) we get y - 2 = 1( x + 1) or y-2=x+1 or y=x+3 point is (-1, 2) m=1

Equation of Tangents Outcome 3 Higher Example 22 Find the equation of the tangent to the curve y = 4 x 2 at the point where x = -2. (x 0) Also find where the tangent cuts the X-axis and Y-axis. Point: when Gradient: x = -2 then y = 4 = (-2)2 y = 4 x-2 when x = -2 then so dy/ dx dy/ = dx -8 = (-2)3 4/ = 1 4 point is (-2, 1) = -8 x-3 = -8/ -8 =1 -8 x 3 m=1

Equation of Tangents Outcome 3 Higher Now using y - b = m(x - a) we get y - 1 = 1( x + 2) or y-1=x+2 or y=x+3 Axes Tangent cuts Y-axis when x = 0 so y = 0 + 3 = 3 at point (0, 3) Tangent cuts X-axis when y = 0 so 0 = x + 3 or x = -3 at point (-3, 0)

Equation of Tangents Outcome 3 Higher Example 23 - (other way round) Find the point on the curve y = x 2 - 6 x + 5 where the gradient of the tangent is 14. gradient of tangent = gradient of curve dy/ so dx = 2 x - 6 = 14 2 x = 20 x = 10 Put x = 10 into y = x 2 - 6 x + 5 Giving y = 100 - 60 + 5 = 45 Point is (10, 45)

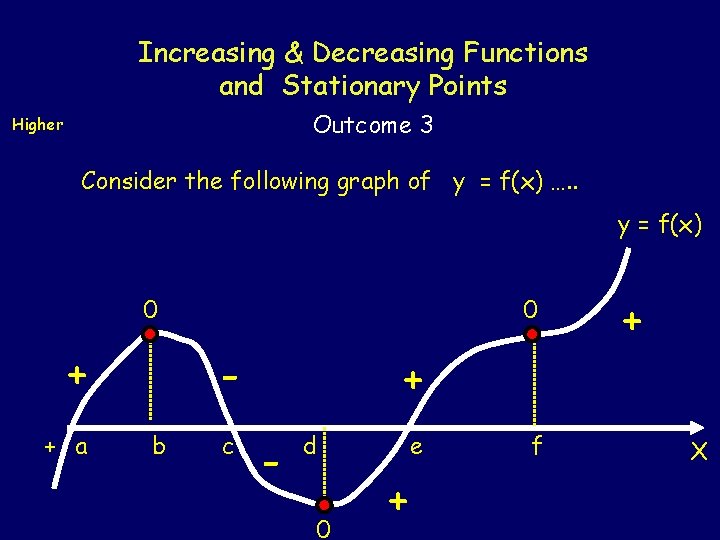
Increasing & Decreasing Functions and Stationary Points Outcome 3 Higher Consider the following graph of y = f(x) …. . y = f(x) 0 + + a 0 b c + - d 0 e + f + X

Increasing & Decreasing Functions and Stationary Points Higher Outcome 3 In the graph of y = f(x) The function is increasing if the gradient is positive i. e. f (x) > 0 when x < b or d < x < f or x > f. The function is decreasing if the gradient is negative and f (x) < 0 when b < x < d. The function is stationary if the gradient is zero and f (x) = 0 when x = b or x = d or x = f. These are called STATIONARY POINTS. At x = a, x = c and x = e the curve is simply crossing the X-axis.

Increasing & Decreasing Functions and Stationary Points Outcome 3 Higher Example 24 For the function f(x) = 4 x 2 - 24 x + 19 determine the intervals when the function is decreasing and increasing. f (x) = 8 x - 24 so 8 x - 24 < 0 8 x < 24 x<3 2 – 24 = -8 f(x) decreasing when f (x) < 0 Check: f (2) = 8 X f(x) increasing when f (x) > 0 Check: f (4) = 8 X 4 – 24 = 8 so 8 x - 24 > 0 8 x > 24 x>3

Increasing & Decreasing Functions and Stationary Points Outcome 3 Higher Example 25 For the curve y = 6 x – 5/x 2 Determine if it is increasing or decreasing when x = 10. y = 6 x - 5 x-2 x 2 so dy/ dx = 6 + 10 x-3 = 6 + 10 x 3 when x = 10 Since dy/ dx = 6+ 10/ 1000 = 6. 01 > 0 then the function is increasing.

Increasing & Decreasing Functions and Stationary Points Higher Outcome 3 Example 26 Show that the function g(x) = 1/3 x 3 -3 x 2 + 9 x -10 is never decreasing. g (x) = x 2 - 6 x + 9 = (x - 3)= (x - 3)2 Squaring a negative or a positive value produces a positive value, while 02 = 0. So you will never obtain a negative by squaring any real number. Since (x - 3)2 0 for all values of x then g (x) can never be negative so the function is never decreasing.

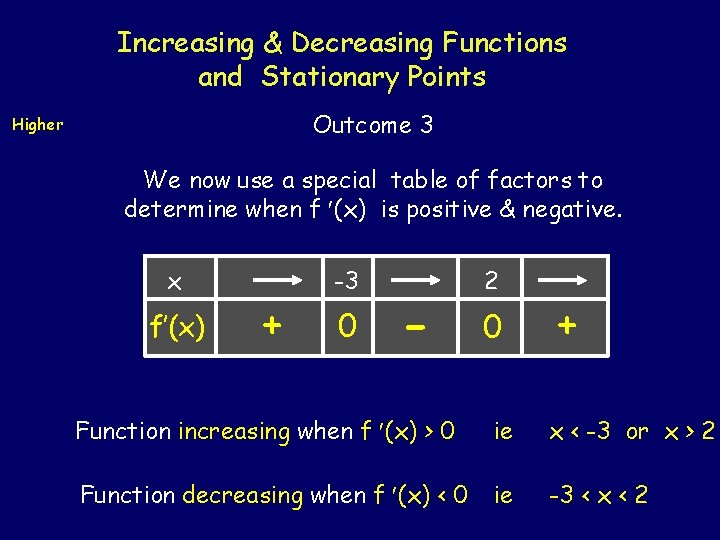
Increasing & Decreasing Functions and Stationary Points Outcome 3 Higher Example 27 Determine the intervals when the function f(x) = 2 x 3 + 3 x 2 - 36 x + 41 is (a) Stationary (b) Increasing (c) Decreasing. f (x) = 6 x 2 + 6 x - 36 = 6(x 2 + x - 6) = 6(x + 3)(x - 2) Function is stationary when f (x) = 0 ie 6(x + 3)(x - 2) = 0 ie x = -3 or x=2

Increasing & Decreasing Functions and Stationary Points Outcome 3 Higher We now use a special table of factors to determine when f (x) is positive & negative. x f’(x) + -3 0 - 2 0 + Function increasing when f (x) > 0 ie x < -3 or x > 2 Function decreasing when f (x) < 0 ie -3 < x < 2

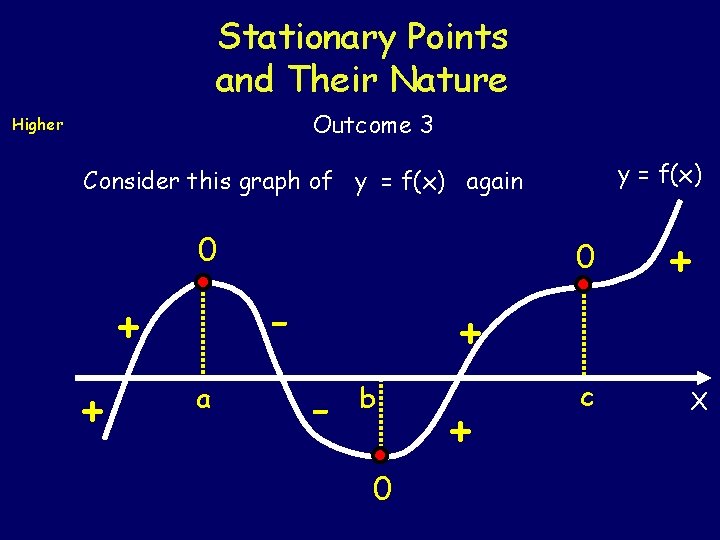
Stationary Points and Their Nature Outcome 3 Higher y = f(x) Consider this graph of y = f(x) again 0 - + + 0 a + + - b 0 + c X

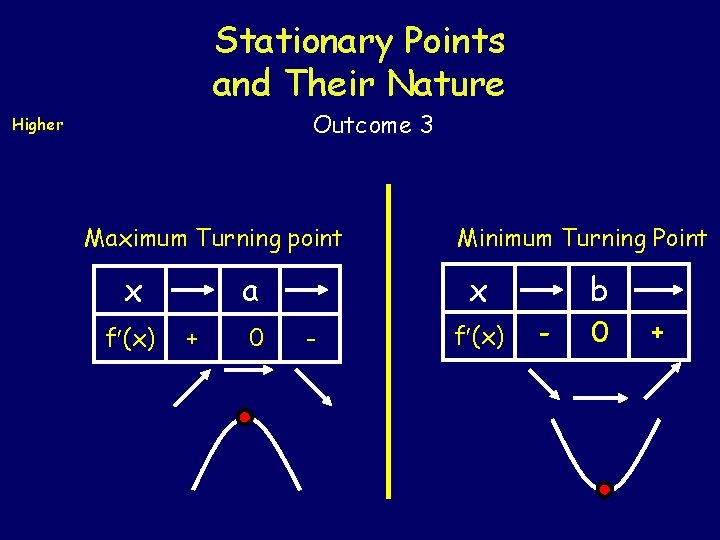
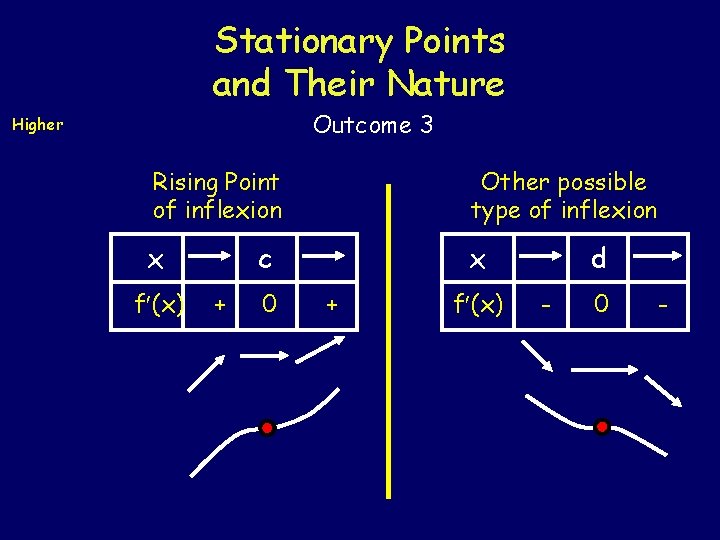
Stationary Points and Their Nature Higher Outcome 3 This curve y = f(x) has three types of stationary point. When x = a we have a maximum turning point (max TP) When x = b we have a minimum turning point (min TP) When x = c we have a point of inflexion (PI) Each type of stationary point is determined by the gradient ( f (x) ) at either side of the stationary value.

Stationary Points and Their Nature Outcome 3 Higher Maximum Turning point x f (x) a + 0 Minimum Turning Point x - f (x) b - 0 +

Stationary Points and Their Nature Outcome 3 Higher Rising Point of inflexion Other possible type of inflexion x x f (x) c + 0 + f (x) d - 0 -

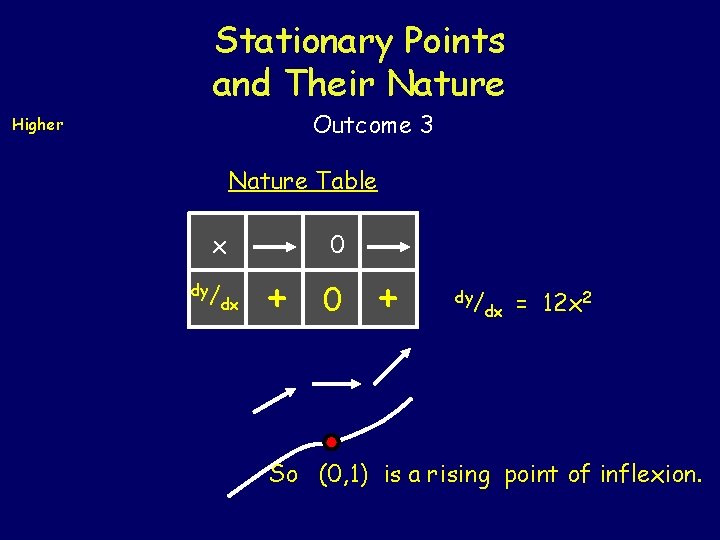
Stationary Points and Their Nature Outcome 3 Higher Example 28 Find the co-ordinates of the stationary point on the curve y = 4 x 3 + 1 and determine its nature. SP occurs when dy/ dx = 0 so 12 x 2 = 0 x= 0 Using y = 4 x 3 + 1 if x = 0 then y = 1 SP is at (0, 1)

Stationary Points and Their Nature Outcome 3 Higher Nature Table x dy/ dx 0 + dy/ dx = 12 x 2 So (0, 1) is a rising point of inflexion.

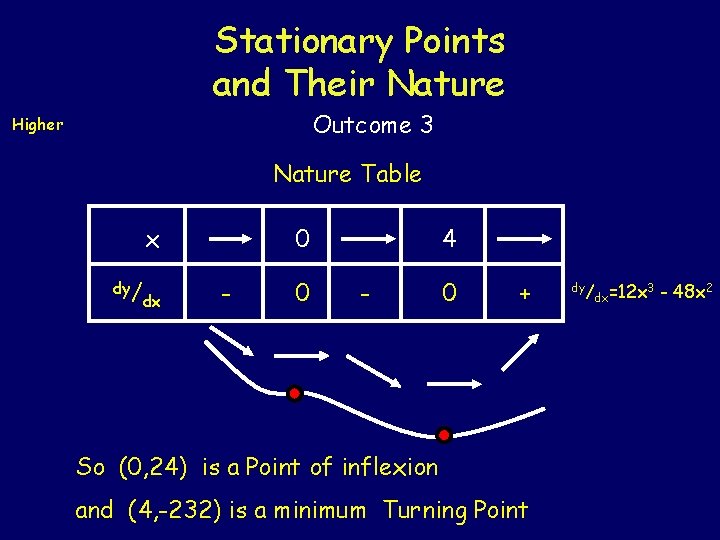
Stationary Points and Their Nature Outcome 3 Higher Example 29 Find the co-ordinates of the stationary points on the curve y = 3 x 4 - 16 x 3 + 24 and determine their nature. SP occurs when dy/ dx = 0 So 12 x 3 - 48 x 2 = 0 12 x 2(x - 4) = 0 12 x 2 = 0 or (x - 4) = 0 x = 0 or x = 4 Using y = 3 x 4 - 16 x 3 + 24 if x = 0 then y = 24 if x = 4 then y = -232 SPs at (0, 24) & (4, -232)

Stationary Points and Their Nature Outcome 3 Higher Nature Table x dy/ dx 4 0 - 0 + So (0, 24) is a Point of inflexion and (4, -232) is a minimum Turning Point dy/ dx=12 x 3 - 48 x 2

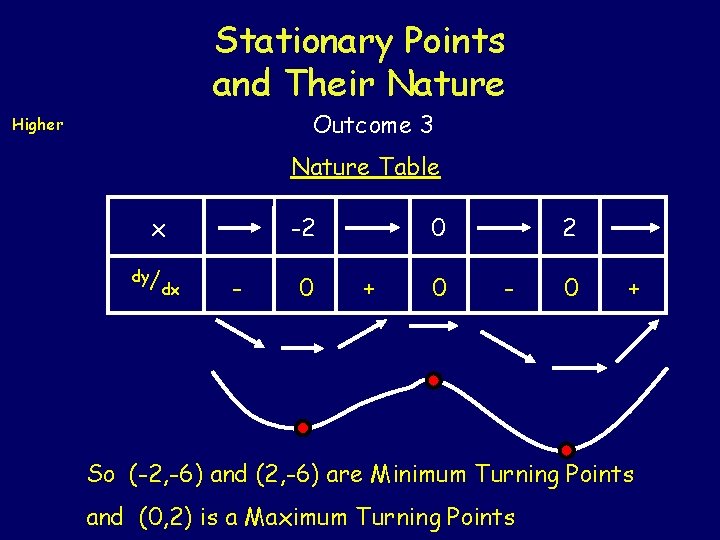
Stationary Points and Their Nature Outcome 3 Higher Example 30 Find the co-ordinates of the stationary points on the curve y = 1/2 x 4 - 4 x 2 + 2 and determine their nature. = 0 Using y = 1/2 x 4 - 4 x 2 + 2 2 x 3 - 8 x = 0 if x = 0 then y = 2 2 x(x 2 - 4) = 0 if x = -2 then y = -6 SP occurs when So dy/ dx 2 x(x + 2)(x - 2) = 0 if x = 2 then y = -6 x = 0 or x = -2 or x = 2 SP’s at(-2, -6), (0, 2) & (2, -6)

Stationary Points and Their Nature Outcome 3 Higher Nature Table x dy/ dx -2 - 0 0 + 0 2 - 0 + So (-2, -6) and (2, -6) are Minimum Turning Points and (0, 2) is a Maximum Turning Points

Curve Sketching Outcome 3 Higher Note: A sketch is a rough drawing which includes important details. It is not an accurate scale drawing. Process (a) Find where the curve cuts the co-ordinate axes. for Y-axis put x = 0 for X-axis put y = 0 then solve. (b) Find the stationary points & determine their nature as done in previous section. (c) Check what happens as x +/- . This comes automatically if (a) & (b) are correct.

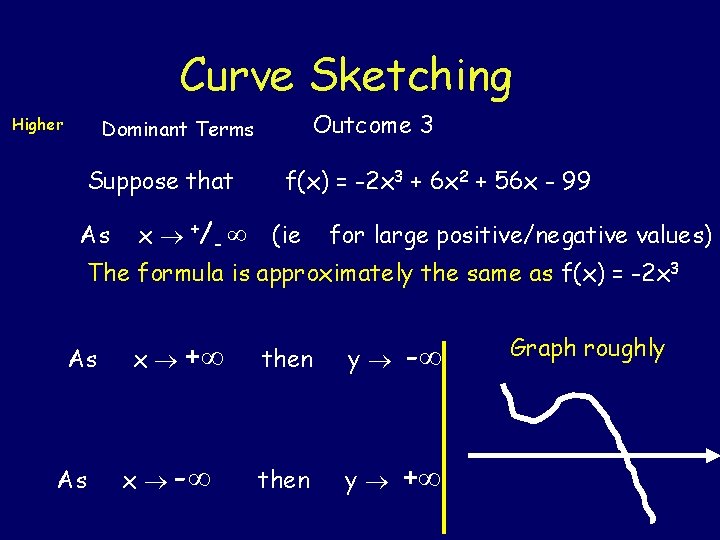
Curve Sketching Higher Outcome 3 Dominant Terms Suppose that As x +/ - f(x) = -2 x 3 + 6 x 2 + 56 x - 99 (ie for large positive/negative values) The formula is approximately the same as f(x) = -2 x 3 As As x + x - then y + Graph roughly

Curve Sketching Outcome 3 Higher Example 31 Sketch the graph of y = -3 x 2 + 12 x + 15 (a) Axes If x = 0 then y = 15 If y = 0 then -3 x 2 + 12 x + 15 = 0 x 2 - 4 x - 5 = 0 (x + 1)(x - 5) = 0 x = -1 or x = 5 Graph cuts axes at (0, 15) , (-1, 0) and (5, 0) ( -3)

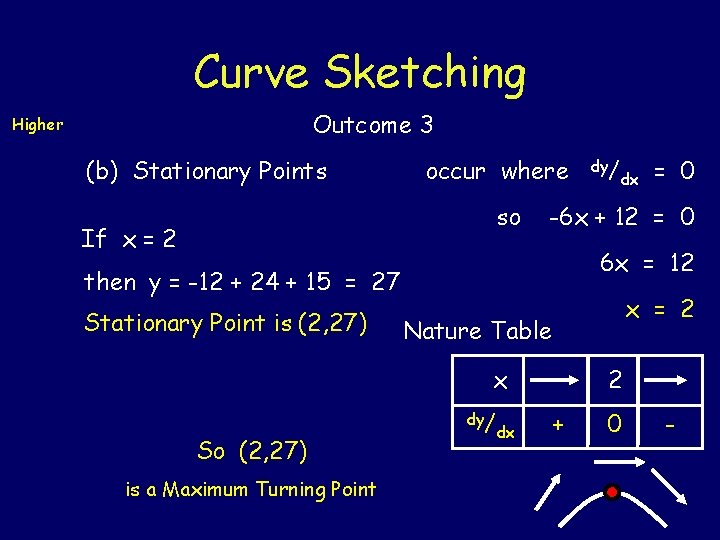
Curve Sketching Outcome 3 Higher (b) Stationary Points occur where so If x = 2 is a Maximum Turning Point = 0 6 x = 12 x = 2 Nature Table x So (2, 27) dx -6 x + 12 = 0 then y = -12 + 24 + 15 = 27 Stationary Point is (2, 27) dy/ dx 2 + 0 -

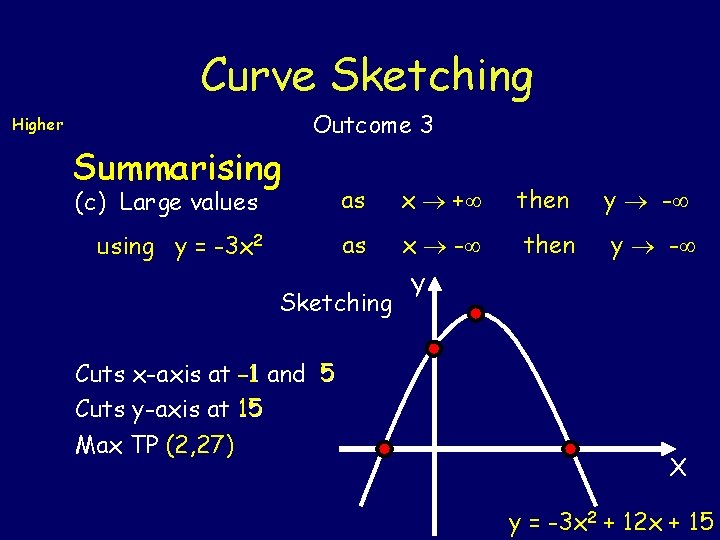
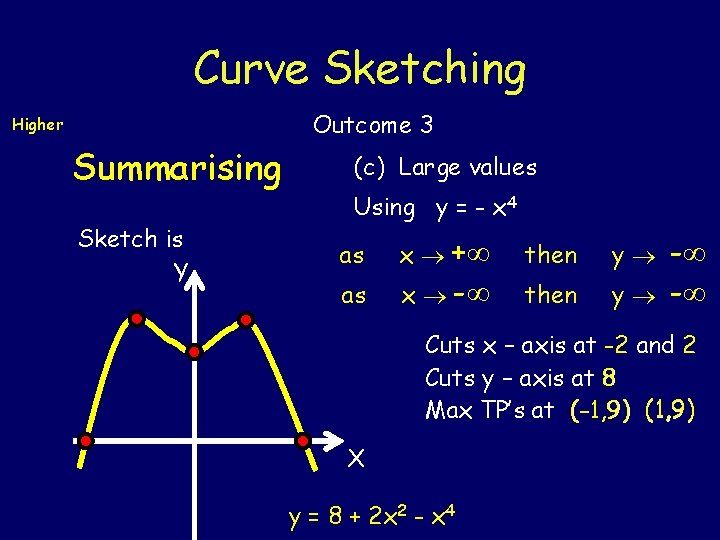
Curve Sketching Higher Summarising Outcome 3 (c) Large values as x + then y - using y = -3 x 2 as x - then y - Sketching Y Cuts x-axis at -1 and 5 Cuts y-axis at 15 Max TP (2, 27) X y = -3 x 2 + 12 x + 15

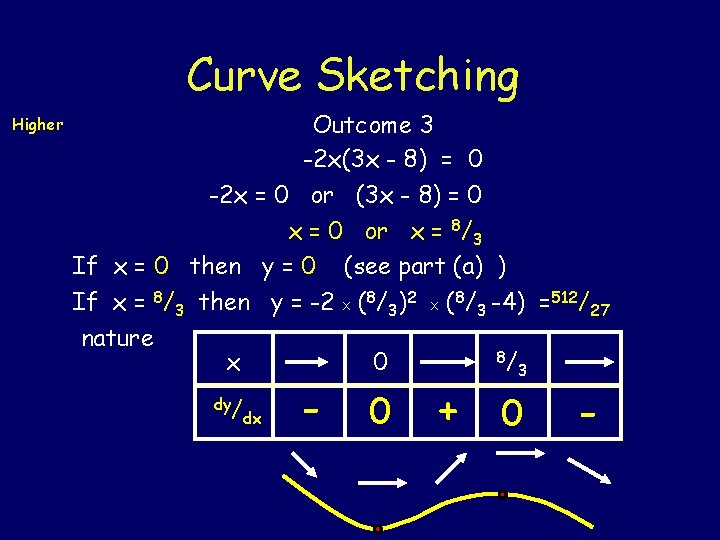
Curve Sketching Outcome 3 Higher Example 32 (a) Axes (b) SPs Sketch the graph of If x = 0 then If y = 0 then -2 x 2 = 0 y = -2 x 2 (x - 4) y = 0 X (-4) = 0 -2 x 2 (x - 4) = 0 or (x - 4) = 0 x = 0 or x = 4 Graph cuts axes at (0, 0) and (4, 0). y = -2 x 2 (x - 4) = -2 x 3 + 8 x 2 SPs occur where so dy/ dx = 0 -6 x 2 + 16 x = 0

Curve Sketching Higher Outcome 3 -2 x(3 x - 8) = 0 -2 x = 0 or (3 x - 8) = 0 x = 0 or x = 8/3 If x = 0 then y = 0 (see part (a) ) If x = 8/3 then y = -2 X (8/3)2 X (8/3 -4) =512/27 nature x dy/ dx - 0 0 8/ 3 + 0 -

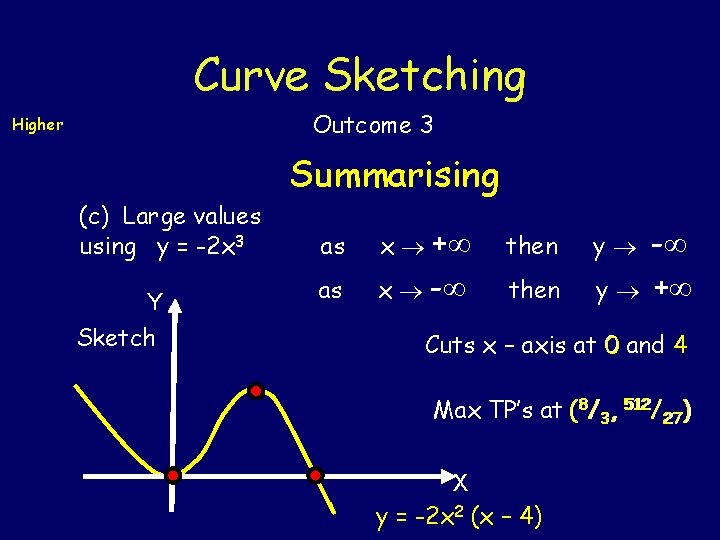
Curve Sketching Outcome 3 Higher Summarising (c) Large values using y = -2 x 3 Y Sketch as as x + x - then y - + Cuts x – axis at 0 and 4 512/ ) Max TP’s at (88/33, 512 27 27 X y = -2 x 2 (x – 4)

Curve Sketching Outcome 3 Higher Example 33 Sketch the graph of (a) Axes y = 8 + 2 x 2 - x 4 If x = 0 then y = 8 If y = 0 then 8 + 2 x 2 - x 4 = 0 Let u = x 2 so u 2 = x 4 (0, 8) Equation is now 8 + 2 u - u 2 = 0 (4 - u)(2 + u) = 0 (4 - x 2)(2 + x 2) = 0 or (2 + x) (2 - x)(2 + x 2) = 0 So x = -2 or x = 2 but x 2 -2 Graph cuts axes at (0, 8) , (-2, 0) and (2, 0)

Curve Sketching Outcome 3 Higher (b) SPs occur where dy/ dx So 4 x - 4 x 3 = 0 4 x(1 - x 2) = 0 4 x(1 - x)(1 + x) = 0 x = 0 or x =1 or x = -1 Using y = 8 + 2 x 2 - x 4 when x = 0 then y = 8 when x = -1 then y = 8 + 2 - 1 = 9 (-1, 9) when x = 1 then y = 8 + 2 - 1 = 9 (1, 9) = 0

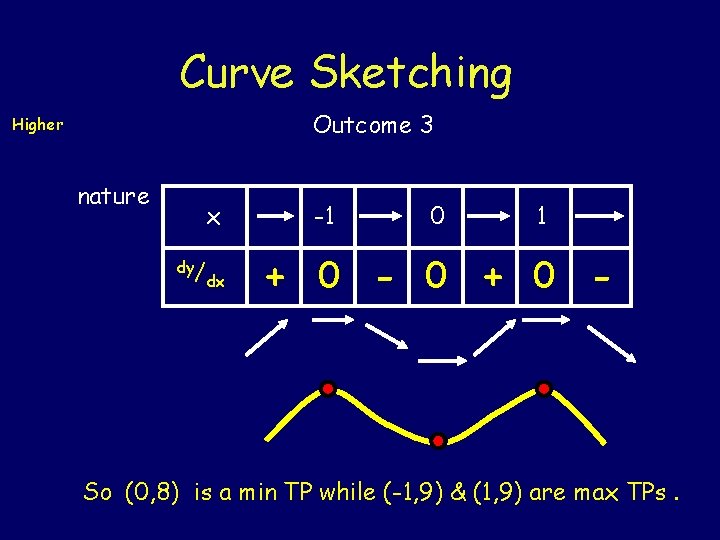
Curve Sketching Outcome 3 Higher nature x dy/ dx -1 0 1 + 0 - 0 + 0 - So (0, 8) is a min TP while (-1, 9) & (1, 9) are max TPs.

Curve Sketching Higher Summarising Sketch is Y Outcome 3 (c) Large values Using y = - x 4 as as x + x - then y - - Cuts x – axis at -2 and 2 Cuts y – axis at 8 Max TP’s at (-1, 9) (1, 9) X y = 8 + 2 x 2 - x 4

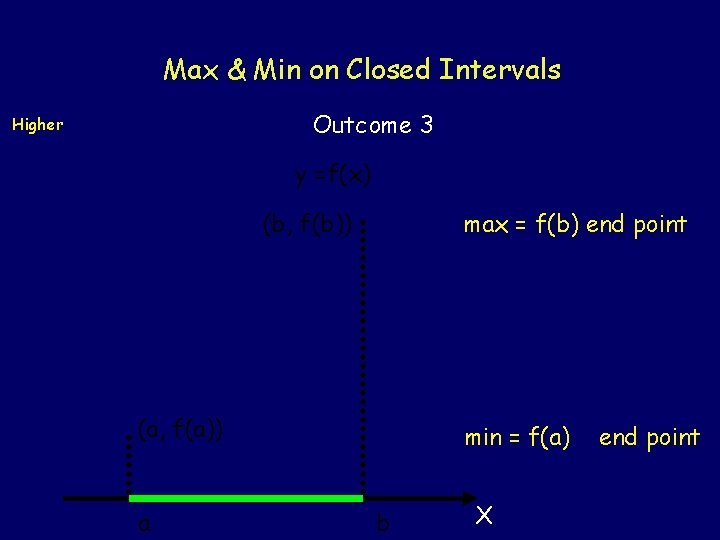
Max & Min on Closed Intervals Higher Outcome 3 In the previous section on curve sketching we dealt with the entire graph. In this section we shall concentrate on the important details to be found in a small section of graph. Suppose we consider any graph between the points where x = a and x = b (i. e. a x b) then the following graphs illustrate where we would expect to find the maximum & minimum values.

Max & Min on Closed Intervals Outcome 3 Higher y =f(x) (b, f(b)) max = f(b) end point (a, f(a)) a min = f(a) b X end point

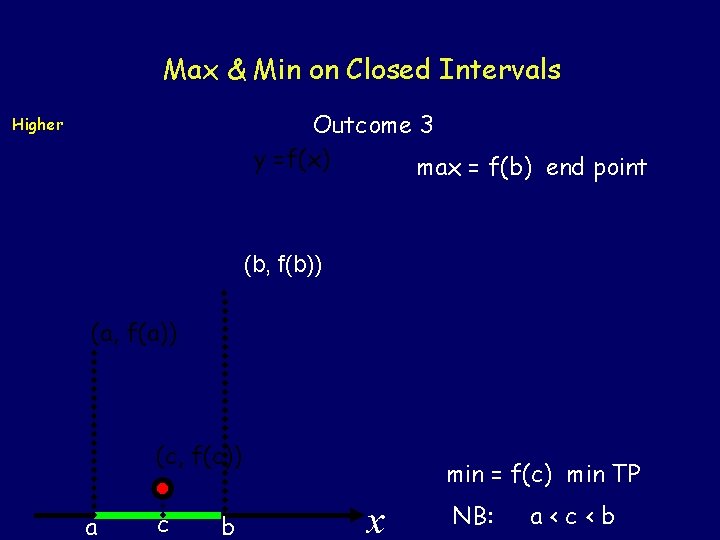
Max & Min on Closed Intervals Outcome 3 Higher (c, f(c)) max = f(c ) max TP (b, f(b)) y =f(x) min = f(a) end point (a, f(a)) a c b x NB: a<c<b

Max & Min on Closed Intervals Outcome 3 y =f(x) max = f(b) end point Higher (b, f(b)) (a, f(a)) (c, f(c)) a c b min = f(c) min TP x NB: a<c<b

Max & Min on Closed Intervals Outcome 3 Higher From the previous three diagrams we should be able to see that the maximum and minimum values of f(x) on the closed interval a x b can be found either at the end points or at a stationary point between the two end points Example 34 Find the max & min values of y = 2 x 3 - 9 x 2 in the interval where -1 x 2. End points If x = -1 then y = -2 - 9 = -11 If x = 2 then y = 16 - 36 = -20

Max & Min on Closed Intervals Outcome 3 Higher Stationary points dy/ dx = 6 x 2 - 18 x = 6 x(x - 3) SPs occur where dy/dx = 0 6 x(x - 3) = 0 6 x = 0 or x - 3 = 0 x = 0 or x = 3 not in interval If x = 0 then y = 0 - 0 = 0 Hence for -1 x 2 , max = 0 & min = -20

Max & Min on Closed Intervals Outcome 3 Higher Extra bit Using function notation we can say that Domain = {x R: -1 x 2 } Range = {y R: -20 y 0 }

Optimization Higher Outcome 3 Note: Optimum basically means the best possible. In commerce or industry production costs and profits can often be given by a mathematical formula. Optimum profit is as high as possible so we would look for a max value or max TP. Optimum production cost is as low as possible so we would look for a min value or min TP.

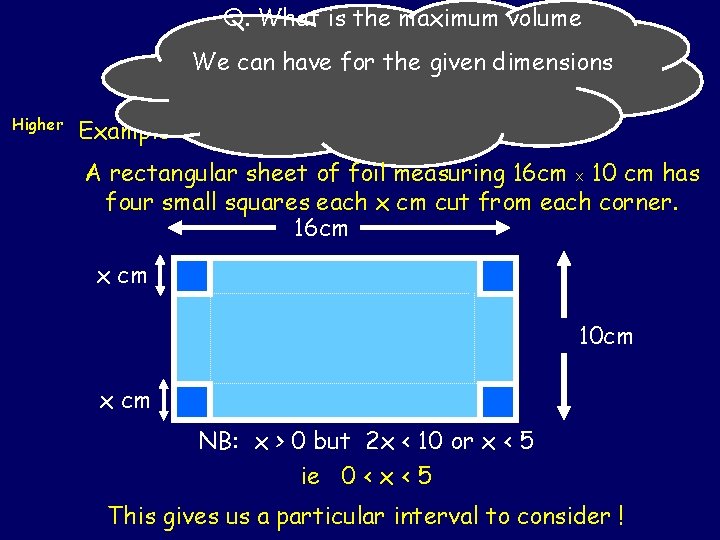
Q. What is the maximum volume We can have for the given dimensions Optimization Higher Example 35 Outcome 3 A rectangular sheet of foil measuring 16 cm X 10 cm has four small squares each x cm cut from each corner. 16 cm x cm 10 cm x cm NB: x > 0 but 2 x < 10 or x < 5 ie 0 < x < 5 This gives us a particular interval to consider !

Optimization Outcome 3 Higher x cm By folding up the four flaps we get a small cuboid (10 - 2 x) cm (16 - 2 x) cm The volume is now determined by the value of x so we can write V(x) = x(16 - 2 x)(10 - 2 x) = x(160 - 52 x + 4 x 2) = 4 x 3 - 52 x 2 +160 x We now try to maximize V(x) between 0 and 5

Optimization Outcome 3 Higher End Points Considering the interval 0 < x < 5 V(0) = 0 X 16 X 10 = 0 V(5) = 5 X 6 X 0 = 0 SPs V '(x) = 12 x 2 - 104 x + 160 = 4(3 x 2 - 26 x + 40) = 4(3 x - 20)(x - 2)

Optimization Outcome 3 Higher SPs occur when V '(x) = 0 ie 4(3 x - 20)(x - 2) = 0 3 x - 20 = 0 or x - 2 = 0 ie x = 20/ 3 or x = 2 not in interval When x = 2 then in interval V(2) = 2 X 12 X 6 = 144 We now check gradient near x = 2

Optimization Outcome 3 Higher Nature x V '(x) + 2 0 - Hence max TP when x = 2 So max possible volume = 144 cm 3

Optimization Higher Example 36 Outcome 3 When a company launches a new product its share of the market after x months is calculated by the formula (x 2) So after 5 months the share is S(5) = 2/5 – 4/25 = 6/25 Find the maximum share of the market that the company can achieve.

Optimization Outcome 3 Higher End points S(2) = 1 – 1 = 0 There is no upper limit but as x S(x) 0. SPs occur where S (x) = 0

Optimization Outcome 3 Higher rearrange 8 x 2 = 2 x 3 8 x 2 - 2 x 3 = 0 2 x 2(4 – x) = 0 x = 0 or x = 4 Out with interval In interval We now check the gradients either side of 4

Optimization Outcome 3 Higher Nature x S (x) + 4 0 - S (3. 9 ) = 0. 00337… S (4. 1) = -0. 0029… Hence max TP at x = 4 And max share of market = S(4) = 2/4 – 4/16 = 1/ 2 – 1/ 4 = 1/ 4

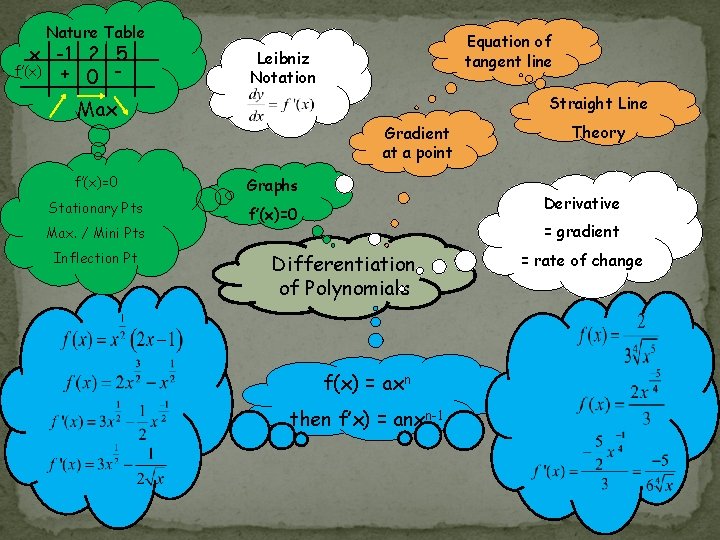
Nature Table x -1 2 5 + 0 - f’(x) Leibniz Notation Straight Line Max Gradient at a point f’(x)=0 Graphs Stationary Pts f’(x)=0 Max. / Mini Pts Inflection Pt Equation of tangent line Theory Derivative = gradient Differentiation of Polynomials f(x) = axn then f’x) = anxn-1 = rate of change
 Differentiation by outcome
Differentiation by outcome Division algorithm
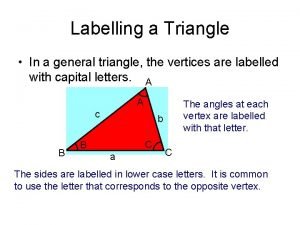
Division algorithm Labelled triangle
Labelled triangle Finding distance with pythagorean theorem
Finding distance with pythagorean theorem Finding and using negotiation power
Finding and using negotiation power Gcf lcm worksheet
Gcf lcm worksheet Venn diagram lcm and hcf
Venn diagram lcm and hcf Obtuse angles trigonometry
Obtuse angles trigonometry Locating the epicenter using triangulation method
Locating the epicenter using triangulation method Finding area using integrals
Finding area using integrals Determine the nature of a stationary point
Determine the nature of a stationary point Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Slidetodoc
Slidetodoc Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Chụp tư thế worms-breton
Chụp tư thế worms-breton Chúa yêu trần thế alleluia
Chúa yêu trần thế alleluia Môn thể thao bắt đầu bằng từ chạy
Môn thể thao bắt đầu bằng từ chạy Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tiính động năng
Công thức tiính động năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 101012 bằng
101012 bằng độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng bé xinh thế chỉ nói điều hay thôi
Cái miệng bé xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Biện pháp chống mỏi cơ
Biện pháp chống mỏi cơ đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Thế nào là giọng cùng tên? *
Thế nào là giọng cùng tên? * Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Các số nguyên tố
Các số nguyên tố Tư thế ngồi viết
Tư thế ngồi viết Lời thề hippocrates
Lời thề hippocrates Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan ưu thế lai là gì
ưu thế lai là gì Sự nuôi và dạy con của hươu
Sự nuôi và dạy con của hươu Sự nuôi và dạy con của hươu
Sự nuôi và dạy con của hươu Hệ hô hấp
Hệ hô hấp Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Automate java application
Automate java application Using system.collections
Using system.collections Defrost using internal heat is accomplished using
Defrost using internal heat is accomplished using Indikator outcome kotaku
Indikator outcome kotaku Maji maji rebellion definition ap world history
Maji maji rebellion definition ap world history Plessy v ferguson outcome
Plessy v ferguson outcome Research project outcome
Research project outcome Causes of renaissance
Causes of renaissance The reformation outcome martin luther and the reformation
The reformation outcome martin luther and the reformation Outcome of prisoner's dilemma
Outcome of prisoner's dilemma Duty of care care certificate
Duty of care care certificate Indikator outcome kotaku
Indikator outcome kotaku Predicted outcome value theory
Predicted outcome value theory Monopoly graph labeled
Monopoly graph labeled Outcome star
Outcome star Contoh input, proses dan output dalam kesehatan
Contoh input, proses dan output dalam kesehatan Outcomes based education for teacher preparation curriculum
Outcomes based education for teacher preparation curriculum Learning outcomes generator
Learning outcomes generator Objective vs outcome
Objective vs outcome Outcome star online
Outcome star online Learning objectives of poem
Learning objectives of poem Measurable outcomes examples
Measurable outcomes examples What was the social cause of french revolution
What was the social cause of french revolution Effects of the american revolution
Effects of the american revolution Mdcps dpgt
Mdcps dpgt Outcome example
Outcome example Decision making with probabilities
Decision making with probabilities Data driven messaging
Data driven messaging Outcome evaluation
Outcome evaluation Monopoly outcome
Monopoly outcome Pediatric physical therapy assessment tools
Pediatric physical therapy assessment tools Result based reporting
Result based reporting Transition learning and development statement examples
Transition learning and development statement examples Outcome harvesting training
Outcome harvesting training Tinker v des moines outcome
Tinker v des moines outcome The renaissance outcome renaissance painters/sculptors
The renaissance outcome renaissance painters/sculptors Contoh penilaian projek
Contoh penilaian projek Intended outcome
Intended outcome District health action plan
District health action plan Arti outcome adalah
Arti outcome adalah Outcome based evaluation
Outcome based evaluation