Labelling a Triangle In a general triangle the

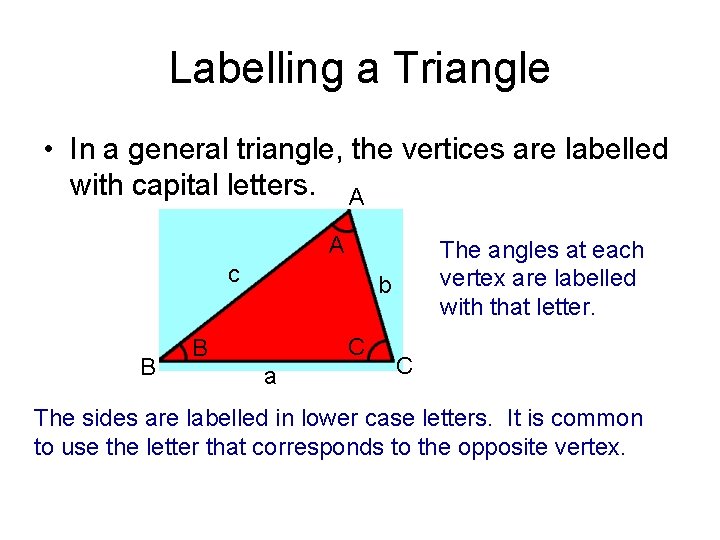
Labelling a Triangle • In a general triangle, the vertices are labelled with capital letters. A A c B The angles at each vertex are labelled with that letter. b C B a C The sides are labelled in lower case letters. It is common to use the letter that corresponds to the opposite vertex.

The sine rule For any triangle ABC, C b A b c a = = sin B sin C sin A a c or B sin A sin B sin C = = a b c

Sine or Cosine? sin A sin B sin C = = a b c cos A = b 2 + c 2 – a 2 2 bc • Which rule should you use if… – You know 3 sides and want to find an angle • Cosine rule. Use the cosine rule if: – You know 2 angles, 1 side and want to find another side Ø You are given three sides • Sine rule – You know 2 sides and the or included angle and want to find the third sideØ You are given two sides and • Cosine rule the included angle – You know 2 angles and want to find the third • Neither!Otherwise, The angles must equal 180°rule use the sine

Using the sine rule to find side lengths If we are given two angles in a triangle and the length of a side opposite one of the angles, we can use the sine rule to find the length of the side opposite the other angle. For example, Find the length of side a B 39° a Using the sine rule, 7 a = sin 39° sin 118° C 7 cm A a = 7 sin 39° x sin 118° a = 9. 82 (to 2 d. p. )

Using the sine rule to find angles If we are given two side lengths in a triangle and the angle opposite one of the given sides, we can use the sine rule to find the angle opposite the other given side. For example, Find the angle at B C 8 cm A 46° 6 cm B Using the sine rule, sin 46° sin B = 8 6 sin 46° x 8 sin B = 6 sin 46° – 1 x 8 B = sin 6 B = 73. 56° (to 2 d. p. )

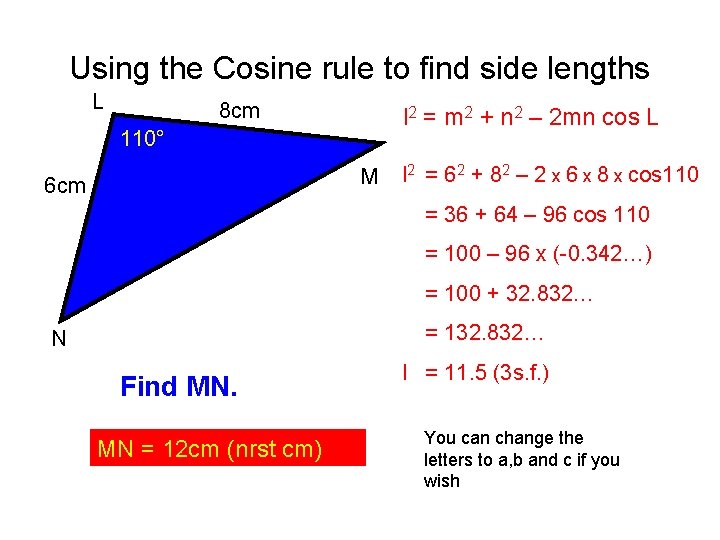
Using the Cosine rule to find side lengths L l 2 8 cm 2 mn cos L l 2 a 2= =mb 22++nc 22–– 2 mn cos A L 2 bc cos 110° M 6 cm m 2 + n 2 l 2 = 62 + 82 – 2 x 6 x 8 x cos 110 = 36 + 64 – 96 cos 110 = 100 – 96 x (-0. 342…) = 100 + 32. 832… = 132. 832… N Find MN. MN = 12 cm (nrst cm) l = 11. 5 (3 s. f. ) You can change the letters to a, b and c if you wish

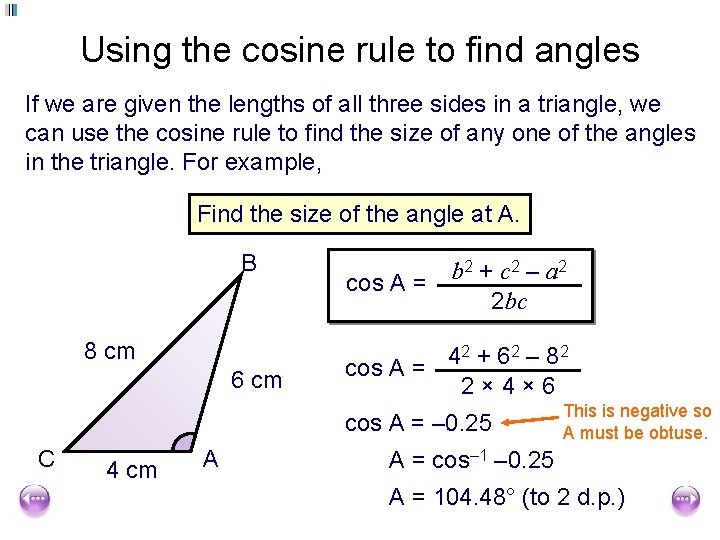
Using the cosine rule to find angles If we are given the lengths of all three sides in a triangle, we can use the cosine rule to find the size of any one of the angles in the triangle. For example, Find the size of the angle at A. B 8 cm 6 cm cos A = b 2 + c 2 – a 2 2 bc 42 + 6 2 – 8 2 cos A = 2× 4× 6 cos A = – 0. 25 C 4 cm A This is negative so A must be obtuse. A = cos– 1 – 0. 25 A = 104. 48° (to 2 d. p. )

The area of a triangle using ½ ab sin C The area of a triangle is equal to half the product of two of the sides and the sine of the included angle. A c B b a Area of triangle ABC = C 1 ab sin C 2