Quiz 2 key The Euclidean Algorithm long division

















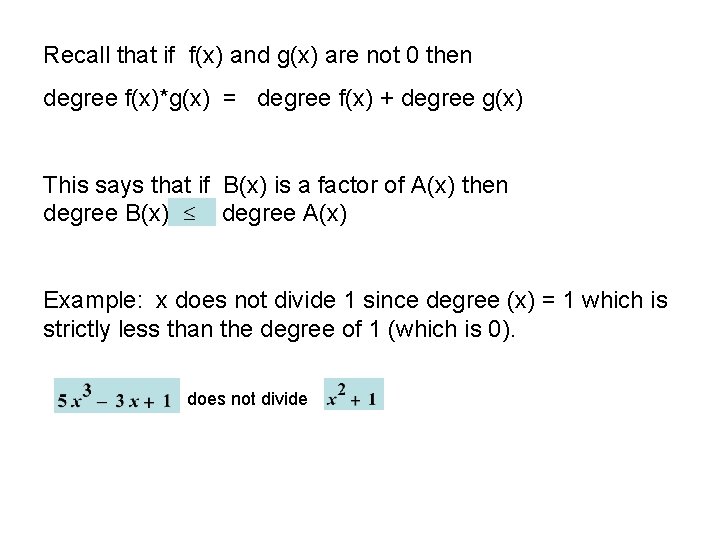















- Slides: 38

Quiz 2 key

The Euclidean Algorithm (long division)

First: The Division algorithm If a and b are integers with b <> 0, then there are unique integers q and r so that a = q b + r and 0 <= r < |b| Example 3745 = __q__ 45 + __r___ Long division: Calculator:

Divisor, common divisor, greatest common divisor b is a divisor of a if a = b*q for some integer q b is common divisor of a and c if _____ b is the greatest common divisor of a and c if ____

Arayabhata-Euclid’s algorithm: How to find gcd(a, b), the greatest common divisor of a and b based on a single observation: if a = b q + r, then any divisor of a and b is also a divisor of r, and any divisor of b and r is also a divisor of a, so gcd(a, b) = gcd(b, r) Euclid algorithm: use the division algorithm repeatedly To reduce the problem to one you can solve. Example: gcd(55, 35) 55 = 35*1 + 20 so gcd(55, 35) = gcd(35, 20) 35 = 20*1 + 15 so gcd(35, 20) = gcd(20, 15) 20 = 15*1 + 5 done gcd(55, 35) = 5

2 columns of the arayabhata table: the columns of quotients and remainders

Writing gcd(a, b) as a linear combination of a and b gcd(55, 35) = 55*x + 35*y : Solve for x and y.

The 1 st column of the arayabhata table

An application Problem: Given a 3 pint can, a 5 pint can, a large tank of water, and a large empty tank, how can we get exactly 1 pint of water into the empty tank?

We will talk about this on Wednesday Division algorithm for polynomials in x. If a(x) and b(x) are polynomials in x then there are unique polynomials q(x) and r(x) so that a(x) = q(x)*b(x) + r(x) where r(x) = 0 or deg(r(x)) < deg(b(x)) Example: x^4 = __q(x)___ (x^2 -1) + __r(x)___ Long division:

Divisor, common divisor, and gcd for polynomials in x b(x) is a divisor of a(x) if ____ c(x) is a common divisor of a(x) and b(x) if ___ c(x) is a greatest common divisor

Recall 4 th grade If A and B are integers (whole numbers) then we say that B divides A if there is an integer Q such that A = BQ Examples: • 2 divides 6 since there is an integer (3) such that 6 = 2*3 • 1 divides any 291 since there is a number (291) such that 291 = 219*1 • If B is any number then B divides 0 since there is a number (0) such that 0 = B*0 • Another way to say that B divides A is to say that B is a factor of A

More examples • 3 does not divide 5 since there is no whole number Q such that 5 = 3*Q • 9 does not divide 10 since there is no whole number Q such that 10 = 9*Q

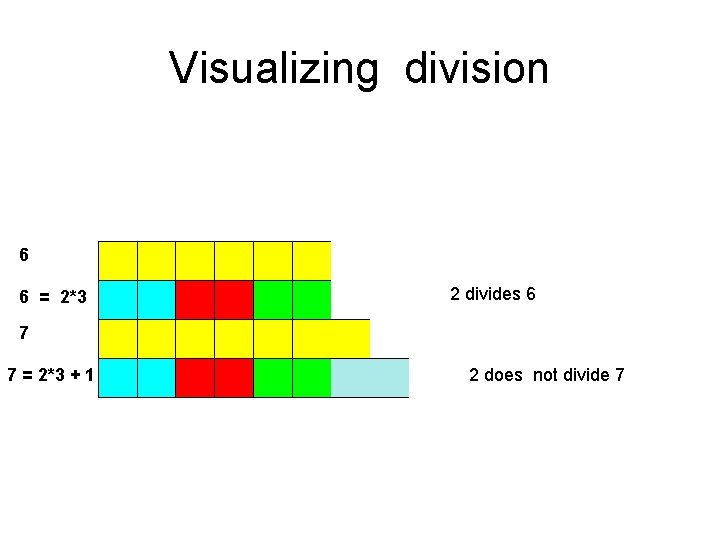
Visualizing division 6 6 = 2*3 2 divides 6 7 7 = 2*3 + 1 2 does not divide 7

Division Algorithm A and B are whole numbers and B is not 0. To determine if B divides A do the following: i. If A = 0 then B divides A ii. If 0 < A < B then B does not divide A ii. If B <= A then replace A by B – A and repeat i. 7 – 2 - 2 – 2 = 7 – 3*2 = 1 < 2 (step 4) 7 – 2 - 2 = 7 – 2*2 = 3 > 2 (step 3) 7 – 1*2 = 5 > 2 7 >2 (step 2) (step 1) The process subtracts B from A as many times as it can. At some point A is reduced to 0 or B cannot be subtracted from what remains. The effect is to write A = BQ + R with R = 0 or 0 < R < B R is called the remainder when A is divided by B. Q is called the quotient.

“Long Division” __3 _ 7 | 220 210 10 31 7 | 220 210 10 _7 3 220 = 7*30 + 10 (does 30 subtractions) 10 > 7 so can subtract more 220 - 7*30 = 1*7 + 3 0 < 3 < 7 process terminates Quotient = 31 remainder = 3 220 = 7*31 + 3

Division Algorithm If A and B are integers with B not zero then there are unique integers Q and R such that A = BQ + R with 0 <= R < |B| Note this allows A and B to be negative 5 = (-2) + 1 0 < 1 <|-2| -7 = (-2)(4) + 1 0 < 1<|-2|

Works Exactly the Same for Polynomials • B(x) divides A(x) if there is a Q(x) so that A(x) = B(x)*Q(x) • Every polynomial divides 0 0 = B(x)*0 • Any non-zero number divides any polynomial (e. g. A(x) = 7*( A(x) ) • x – 1 divides since
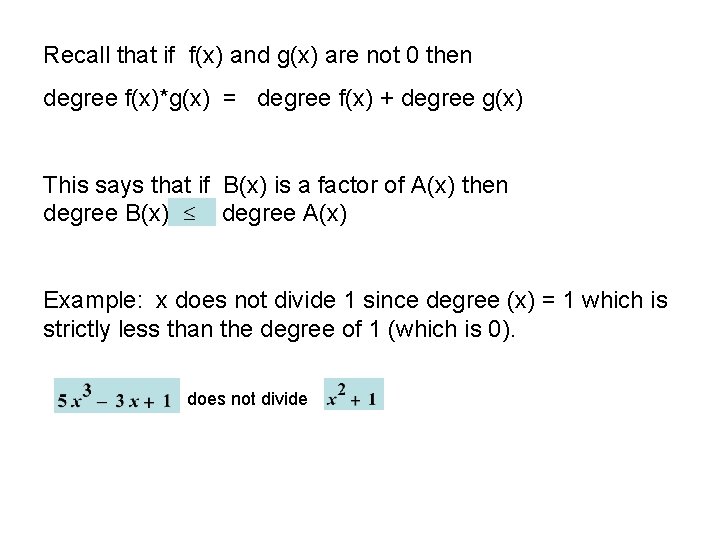
Recall that if f(x) and g(x) are not 0 then degree f(x)*g(x) = degree f(x) + degree g(x) This says that if B(x) is a factor of A(x) then degree B(x) degree A(x) Example: x does not divide 1 since degree (x) = 1 which is strictly less than the degree of 1 (which is 0). does not divide

Division Algorithm for Polynomials If A(x) and B(x) are polynomials with B not zero then there are unique polynomials Q(x) and R(x) such that A(x) = B(x)Q(x) + R(x) with R(x)=0 or degree R(x) < degree B(x) Note that R(x) = 0 is another way to say that B(x) divides A(x).

The Long Division of Polynomials is a Way to calculate Q(x) and R(x) Observations: To calculate Q(x) and R(x) it suffices to find R(x) since we can divide A(x)- R(x) by B(x) to get R(x) The uniqueness of the remainder says if in any way you arrange to write A(x) = B(x)K(x) + P(x) where P(x) is zero or of smaller degree than B(x) then it must be that P(x) is the R(x) you would get by long division. For instance : is divided by x-1 will be x. Also which says that the remainder when so is divided by x -1 is 1.

Algebra of Remainders (modular arithmetic) Principle: When calculating the remainder when an algebraic expression of polynomials is divided by a polynomial B, one can replace any factor or summand by its remainder upon division by B. The remainder upon dividing the sum of two polynomials by B is the same as the remainder if either (or both) terms is first replaced by its remainder (or any polynomial that has the same remainder). The remainder upon dividing the product of two polynomials by B is the same as the remainder if either (or both) terms is first replaced by its remainder (or any polynomial that has the same remainder).

Calculate the remainder upon division of by First note that since We can replace the remainder of by its remainder 1 -x = = Now we can replace again to get is

Similarly Calculate the remainder when is divided by As with the previous example the remainder of is 2 x+1 is the same as the remainder of or = This says for some polynomial Q(x) is a root of Replace x by Since it is a root of . What is in we have or

The Greatest Common Divisor (GCD) (also called GCFactor) • The GCD of two integers A 1 and A 2 is the largest integer that divides both. – Examples: gcd(n, 1)=1 for any n – gcd(n, 0) = |n| if n is not 0 • (gcd(0, 0) does not exist • GCD 12 and 20 – – Factors of 12 = {-12, -6, -4, -3, -2, -1, 1, 2, 3, 4, 6, 12} Factors of 20 = {-20, -10, -5, -4, -2, -1, 1, 2, 4, 5, 10, 20} Common factors = {-4, -2, -1, 1, 2, 4} Greatest common factor = 4 • Not a practical for large numbers

• Factors of 5280 • Factors of 4680 GCD(5280, 4680) = ?

• 146057167872 has 1056 positive factors • 5228296875 has 120 positive factors • There is no known way to find a single factor (other than itself and 1) of a randomly chosen number in a “small” number of steps. • We can find the GCD of pairs of HUGE numbers in a small number of steps.

Theorem: If A, B, d and n are numbers and d divides both A and B then it also divides both A and B+/-n*A Proof: A = d*r B = d*s n*A = d*(n*r) B + n*A = d*s +/- d*(n*r) = d*(s +/- n*r) Theorem: GCD(A, B) = GCD(A, B+/- n*A)

Using this over and over … GCD(146057167872, 5228296875) = GCD(146057167872 – 27* 5228296875, 5228296875) = GCD(4893152247, 5228296875) = GCD(5228296875 - 1*4893152247, 4893152247) = GCD(335144628, 4893152247 ) = GCD(4893152247 -14* 335144628, 335144628 ) = GCD(201127455, 335144628) = GCD( 201127455, 335144628 - 1*201127455 ) = GCD( 201127455, 134017173) = GCD( 201127455 – 1*134017173, 134017173) = GCD( 67110282, 134017173 – 1* 67110282) =GCD(67110282, 66906891)= GCD(67110282 -328* 66906891, 66906891)=GCD(203391, 66906891)= GCD(203391, 66906891 -328*203391) =GCD(203391, 194634) = GCD(203391 -1*194634, 194634) = GCD(8748, 194634 -22*8748) = GCD(8748, 2187) = GCD(8748 -4*2187, 2187) = GCD(2187, 0) So we calculated the GCD without factoring. It has to stop because each time we subtracted a multiple of the smaller from the larger so that the resulting number is even smaller. Process has to eventually get to 0.

Euclid Algorithm To find the gcd of numbers A 1 and A 2 with A 1 > A 2 >= 0 a. If A 2 = 0 then gcd = A 1 b. If A 2 > 0 then A 1 = A 2 q 2 + A 3 with A 2>A 3 >=0 c. Replace A 1 by A 2, A 2 by A 3 and go to step a. d. This is exactly what we did in the previous example. e. Example: gcd(120, 85) f. 120 = 85*1 + 35 g. 85 = 35*2 + 15 h. 35 = 15*2 + 5 i. 15 = 5*3 + 0 gcd = 5 (gcd is the last non-zero remainder)

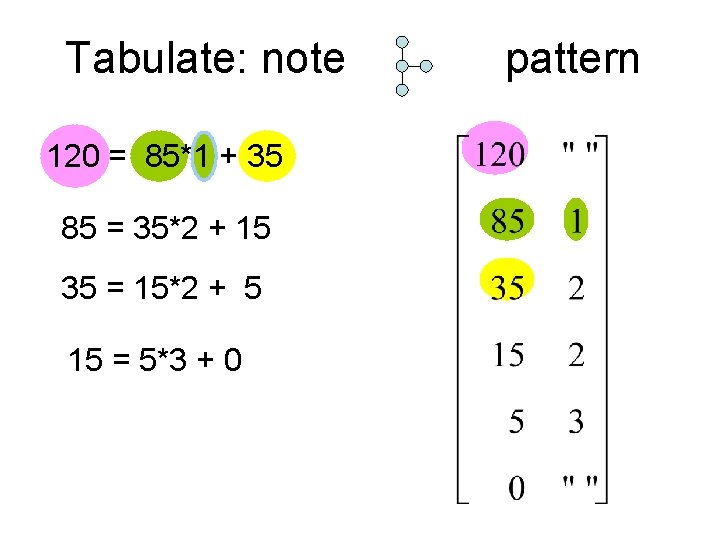
Tabulate: note 120 = 85*1 + 35 85 = 35*2 + 15 35 = 15*2 + 5 15 = 5*3 + 0 pattern

Find numbers a, n so we can write GCD(120, 85) = a*120 - b*85 Idea: find a, b for the last two then modify them to serve for the previous pair. Last pair = 5, 0 GCD=5 obviously 5*1 – 0*0 = 5 Add column to left + - 5*1 – 0*0 = 5 (gcd)

First: Fill in columns 2 and 3 1*5 – 0*0 = 5 ( the gcd) Now want a and b so that a*15+b*5 = 5 Have which says 15=5*3+0 or 15 – 5*3 = 0 Substituting in the first equation 1*5 – 0*(15 – 5*3) = 5 1*5 +(0*3)*5 -0*15 = 5 (1+0*3)*5 - 0*15 = 5

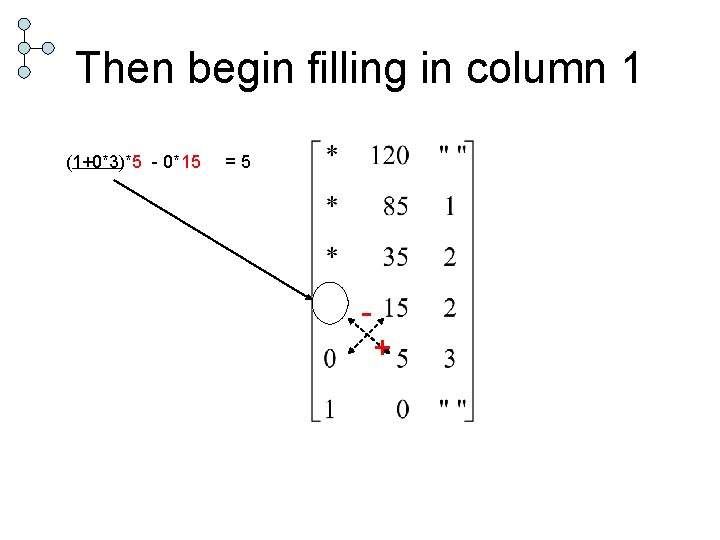
Then begin filling in column 1 (1+0*3)*5 - 0*15 =5 +

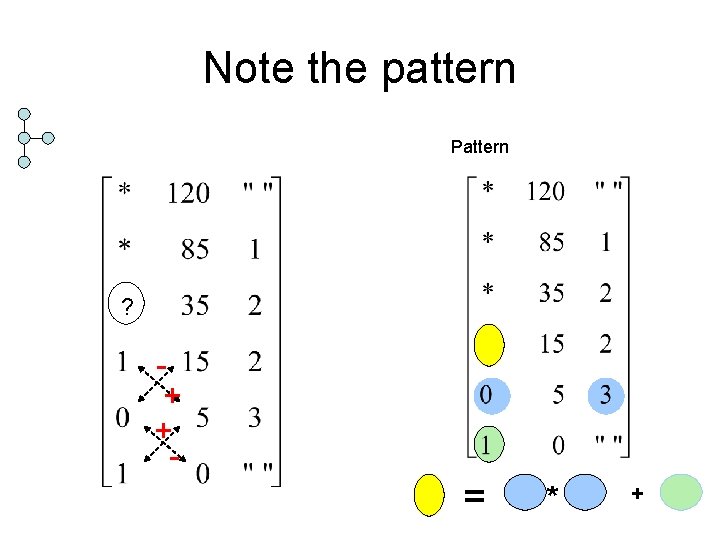
Note the pattern Pattern ? - + + - = * +

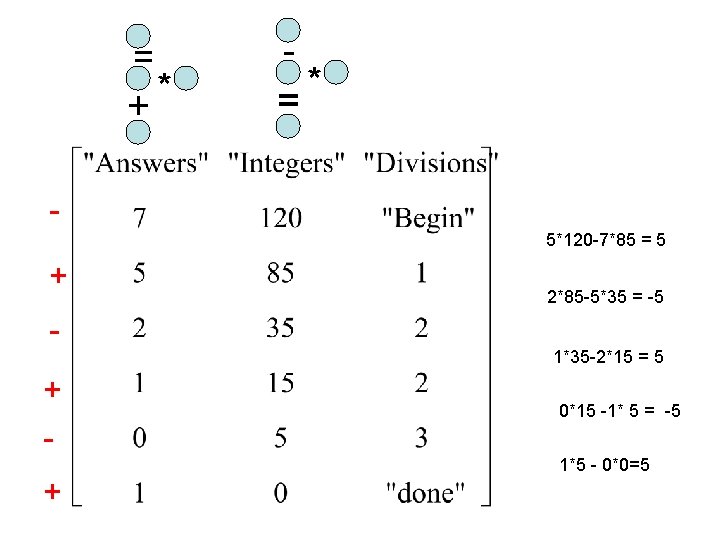
= + * - = * 5*120 -7*85 = 5 + + + 2*85 -5*35 = -5 1*35 -2*15 = 5 0*15 -1* 5 = -5 1*5 - 0*0=5

Same thing works with polynomials Note we are differing from the book slightly. The book would ask that the gcd be monic. That is it wants the gcd in this problem to be x-2 so it would put a ¼ at the lower left instead of 1. Multiply through by ¼ to write x – 2 as a combination of and

1*( )-( )*( ) = -3 - 3 x Lead coefficient of the gcd is -3. Monic gcd is (-3 -3 x)/(-3) = 1+x. Divide both sides by -3 to get monic gcd as a linear combination.