Integration and Area Foundation Definite Integrals Todays Goals






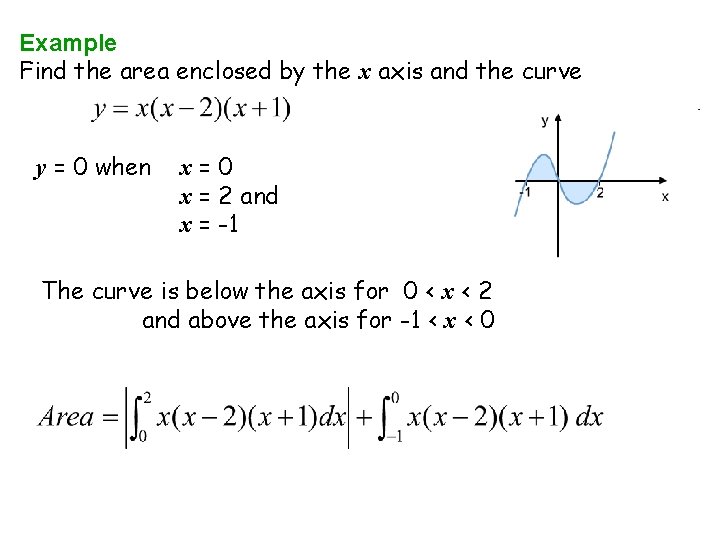

- Slides: 21

Integration and Area Foundation- Definite Integrals

Today’s Goals –To understand why Integration can find the area under a Curve –To Introduce definite Integrals Recap We have already Introduced Integration as the inverse of Differentiation We know that we add a constant for INDEFINITE Integrals and that

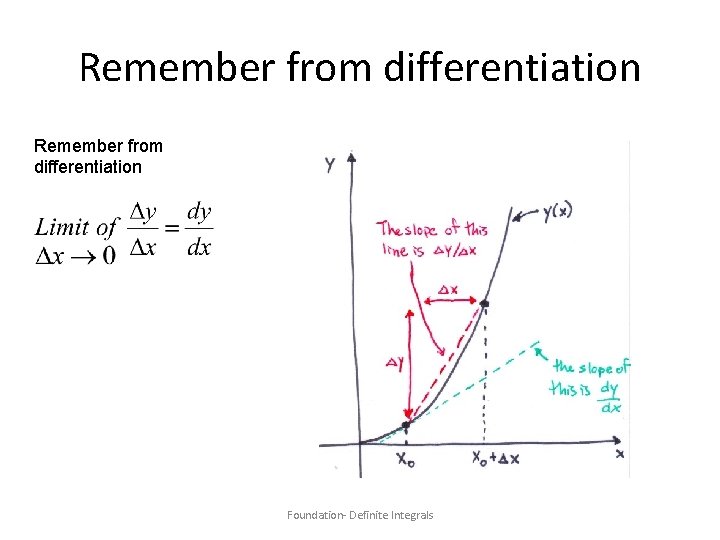
Remember from differentiation Foundation- Definite Integrals

What is integration Integration is summing things up It means to piece things together , to add things up !! Foundation- Definite Integrals

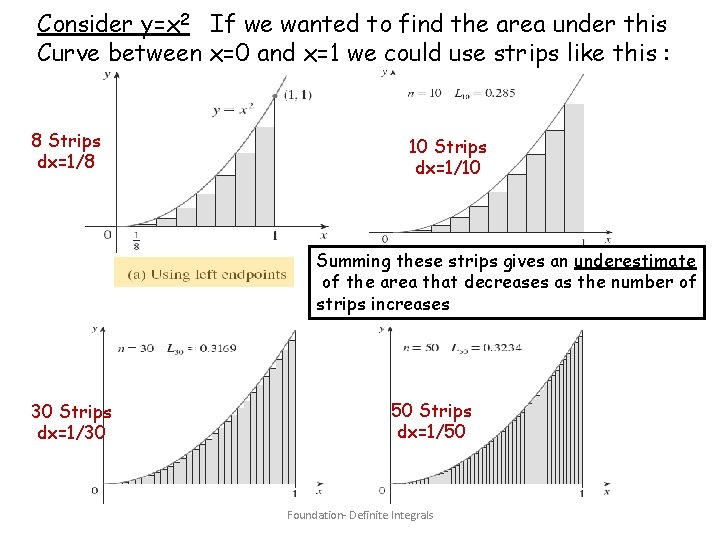
Consider y=x 2 If we wanted to find the area under this Curve between x=0 and x=1 we could use strips like this : 8 Strips dx=1/8 10 Strips dx=1/10 Summing these strips gives an underestimate of the area that decreases as the number of strips increases 30 Strips dx=1/30 50 Strips dx=1/50 Foundation- Definite Integrals

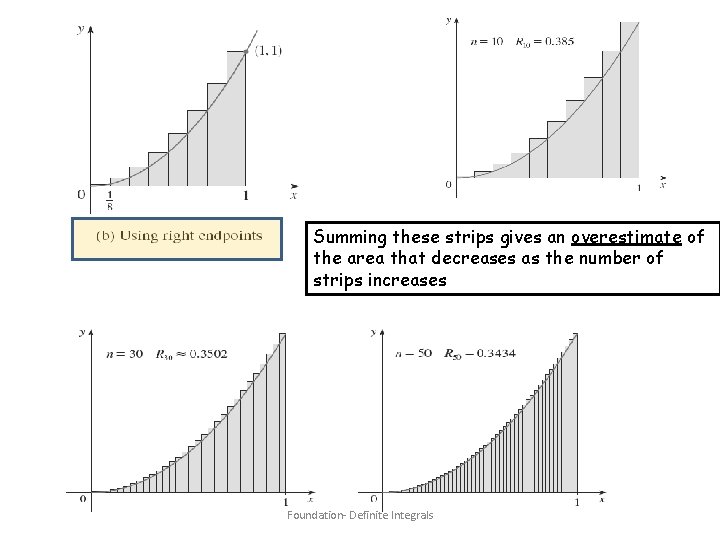
Summing these strips gives an overestimate of the area that decreases as the number of strips increases Foundation- Definite Integrals

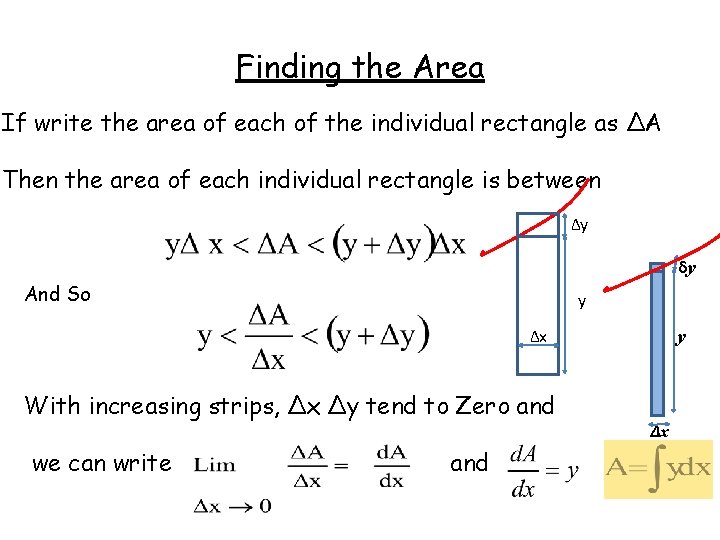
Finding the Area If write the area of each of the individual rectangle as ∆A Then the area of each individual rectangle is between ∆y δy And So y ∆x With increasing strips, ∆x ∆y tend to Zero and we can write and y Δx

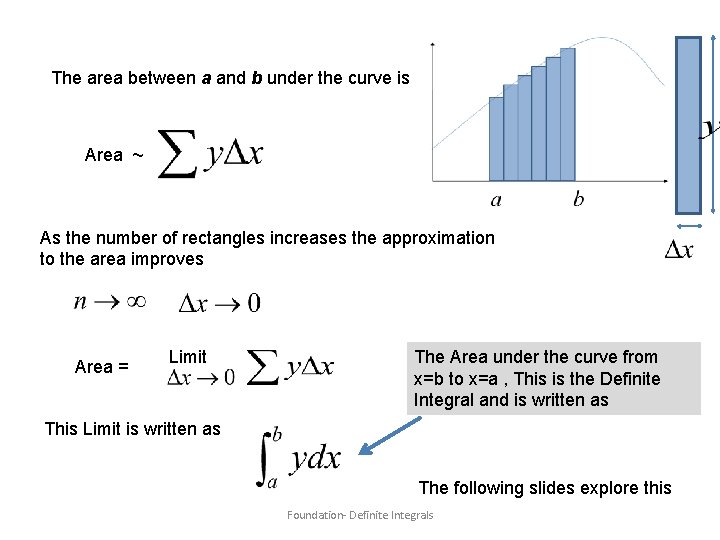
The area between a and b under the curve is Area ~ As the number of rectangles increases the approximation to the area improves Area = Limit The Area under the curve from x=b to x=a , This is the Definite Integral and is written as This Limit is written as The following slides explore this Foundation- Definite Integrals

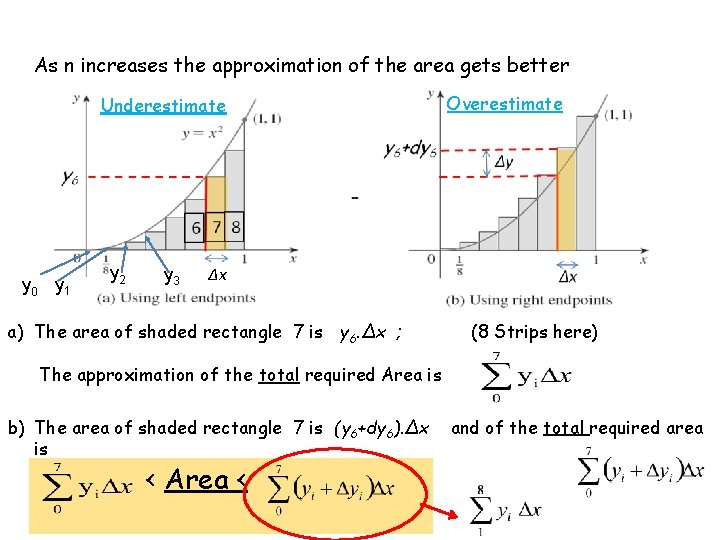
As n increases the approximation of the area gets better Underestimate y 0 y 1 y 2 y 3 Overestimate ∆x Δx a) The area of shaded rectangle 7 is y 6. Δx ; (8 Strips here) The approximation of the total required Area is b) The area of shaded rectangle 7 is (y 6+dy 6). Δx is < Area < and of the total required area

< Area < where ∆A is difference in areas let n →∞ and so ∆x, ∆y, ∆A → 0 Taking an infinite amount of rectangles Limit This RHS is the definition of the 1 st derivative Limit ∆X→ 0 Foundation- Definite Integrals

Change in Area With respect to (w. r. t) Change in x And So And so this leaves RHS because Limit ∆X→ 0 Using our knowledge of taking antiderivatives This is the value of x at the far side of the curve Foundation- Definite Integrals This is the value of x at the near side curve

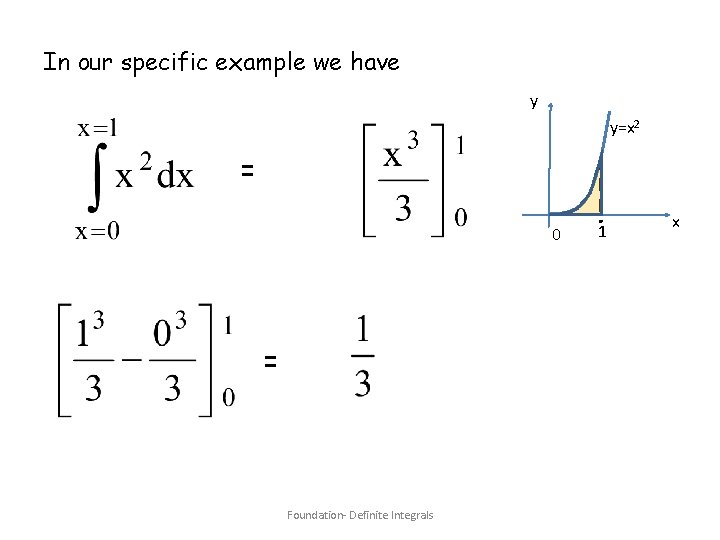
In our specific example we have y y=x 2 = 0 = Foundation- Definite Integrals 1 x

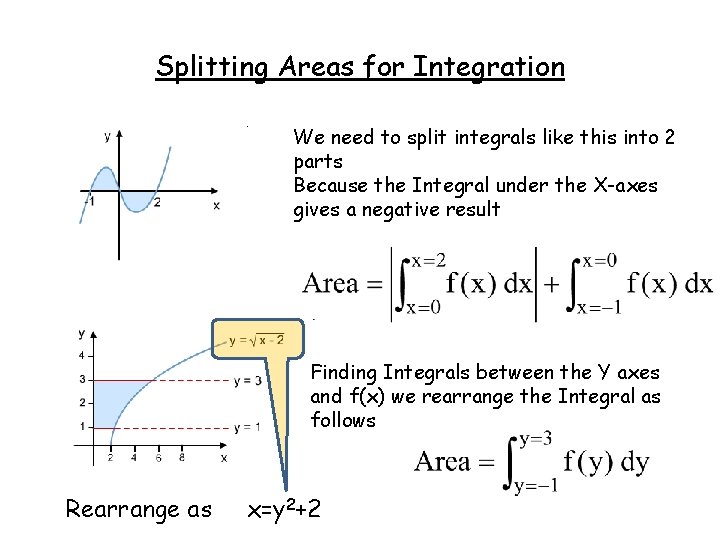
Splitting Areas for Integration Where a curve is below the x-axis the integral is negative Therefore if the curve crosses the x axis we need to split the integration into seperate parts where |x| (the ‘modulus of x’) means the positive value of x
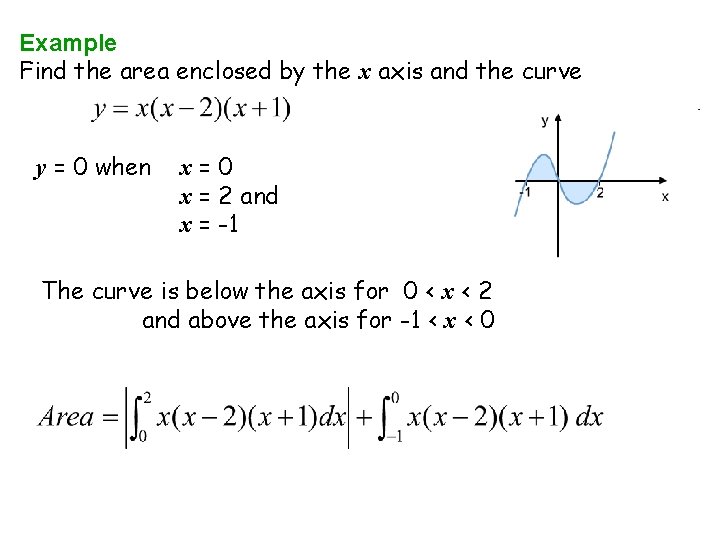
Example Find the area enclosed by the x axis and the curve y = 0 when x=0 x = 2 and x = -1 The curve is below the axis for 0 < x < 2 and above the axis for -1 < x < 0

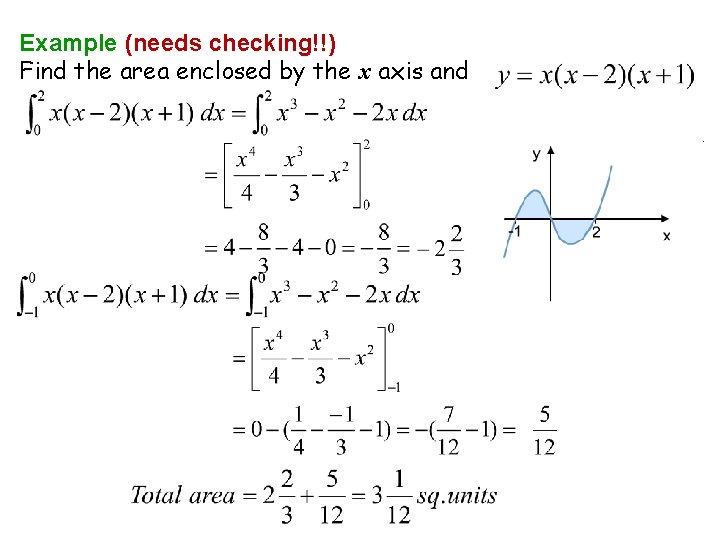
Example (needs checking!!) Find the area enclosed by the x axis and

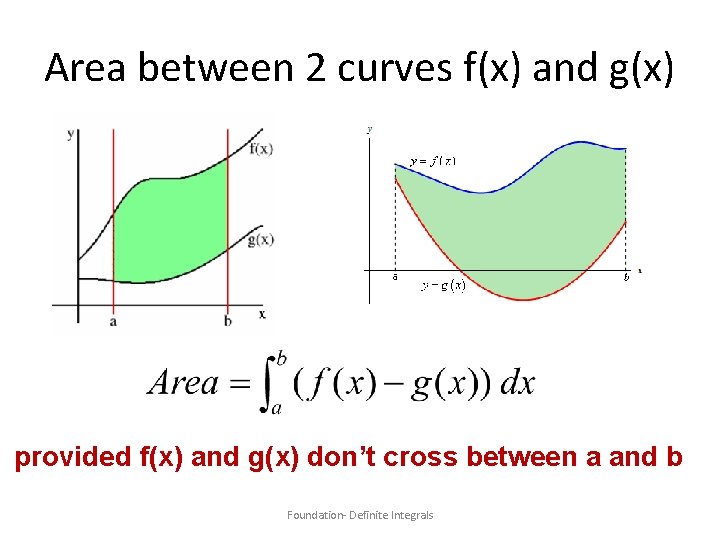
Area between 2 curves f(x) and g(x) provided f(x) and g(x) don’t cross between a and b Foundation- Definite Integrals

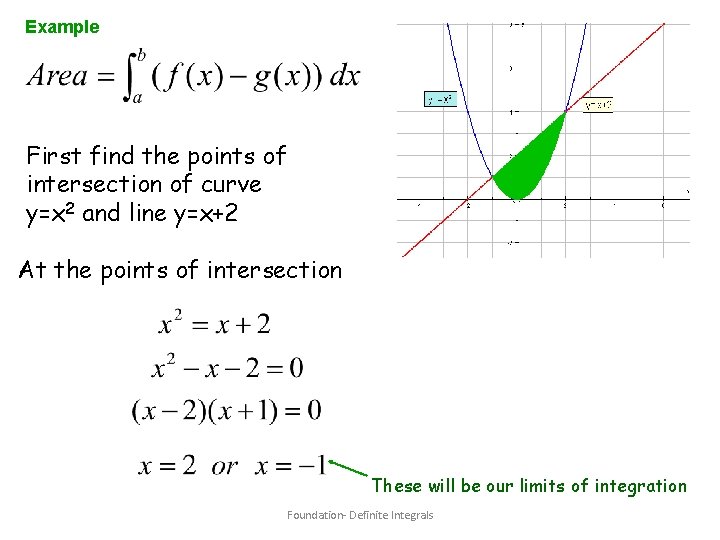
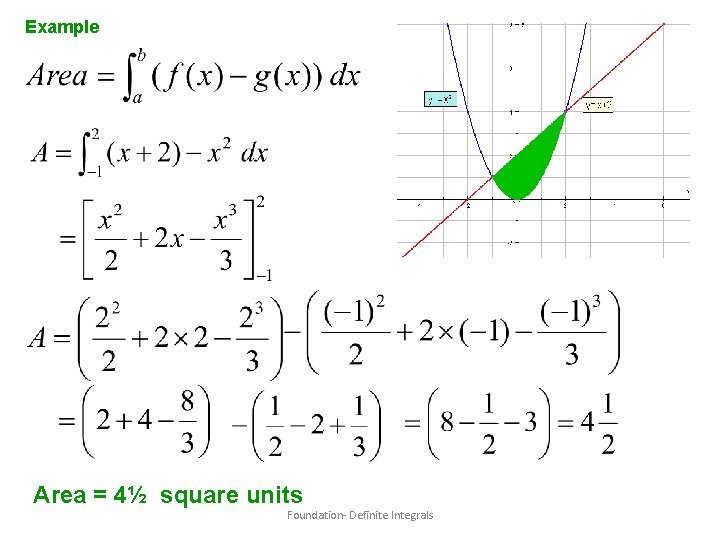
Example First find the points of intersection of curve y=x 2 and line y=x+2 At the points of intersection These will be our limits of integration Foundation- Definite Integrals

Example Area = 4½ square units Foundation- Definite Integrals

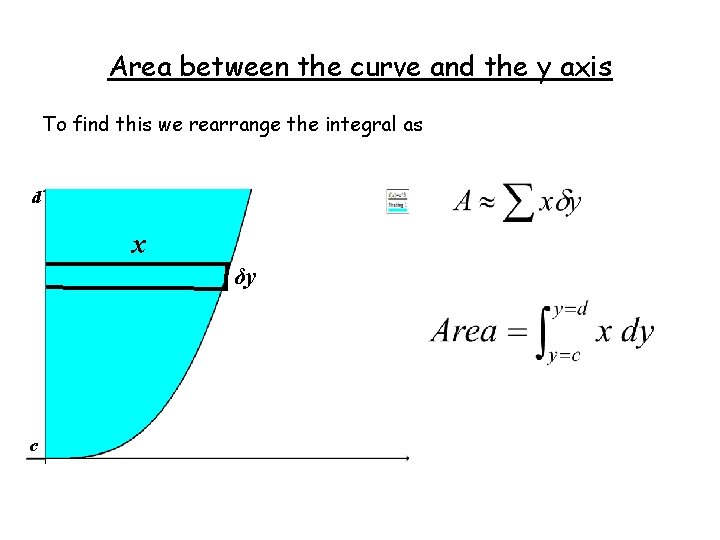
Area between the curve and the y axis To find this we rearrange the integral as d x δy c

Area between the curve and the y axis Rearrange as x=y 2+2 Area = 12 2/3 square units

Splitting Areas for Integration We need to split integrals like this into 2 parts Because the Integral under the X-axes gives a negative result Finding Integrals between the Y axes and f(x) we rearrange the Integral as follows Rearrange as x=y 2+2
 The substitution rule for definite integrals
The substitution rule for definite integrals Sigma notation integral
Sigma notation integral Integral vs definite integral
Integral vs definite integral Norm of a partition
Norm of a partition Max min inequality definite integrals
Max min inequality definite integrals Exploration 1-3a introduction to definite integrals
Exploration 1-3a introduction to definite integrals Circuit training properties of definite integrals
Circuit training properties of definite integrals Strategic goals tactical goals operational goals
Strategic goals tactical goals operational goals Strategic goals tactical goals operational goals
Strategic goals tactical goals operational goals Area under the curve
Area under the curve Inverse chain rule
Inverse chain rule General goals and specific goals
General goals and specific goals Motivation in consumer behaviour
Motivation in consumer behaviour Radiation integrals and auxiliary potential functions
Radiation integrals and auxiliary potential functions Fourier series and integrals
Fourier series and integrals Integrals involving powers of secant and tangent
Integrals involving powers of secant and tangent Three dimensions of corporate strategy
Three dimensions of corporate strategy Vertical integration
Vertical integration Simultaneous integration and sequential integration
Simultaneous integration and sequential integration Pad foundation section
Pad foundation section Composition of urine slideshare
Composition of urine slideshare Team foundation server office integration
Team foundation server office integration