HCF LCM Prime Factorisation Worksheet A Worksheets increase



- Slides: 14

HCF & LCM – Prime Factorisation – Worksheet A Worksheets increase in difficulty and are in 2 sizes

Printing To print handouts from slides Select the slide from the left. Then click: File > Print > ‘Print Current Slide’ To print multiple slides Click on a section title to highlight all those slides, or press ‘Ctrl’ at the same time as selecting slides to highlight more than one. Then click: File > Print > ‘Print Selection’ To print double-sided handouts Highlight both slides before using ‘Print Selection’. Choose ‘Print on Both Sides’ and ‘Flip on Short Edge’.

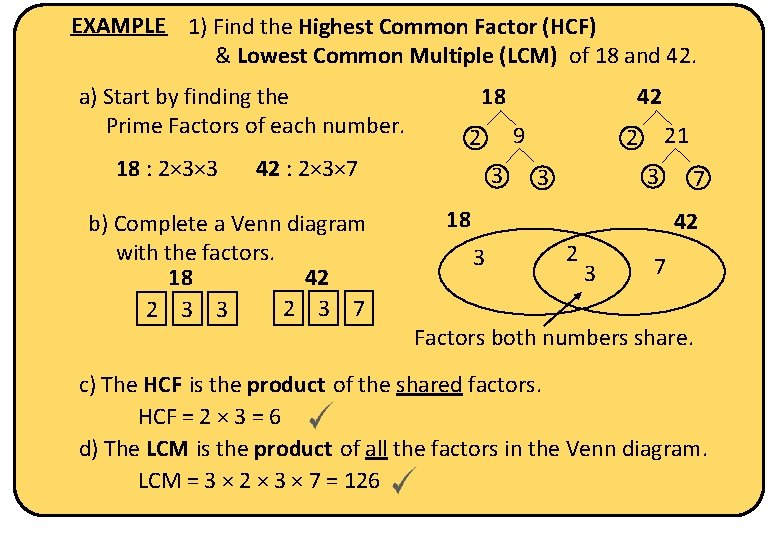
EXAMPLE 1) Find the Highest Common Factor (HCF) & Lowest Common Multiple (LCM) of 18 and 42. a) Start by finding the Prime Factors of each number. 18 : 2× 3× 3 18 b) Complete a Venn diagram with the factors. 18 42 2 3 7 2 3 3 9 2 42 : 2× 3× 7 42 3 21 2 3 3 18 7 42 3 7 Factors both numbers share. c) The HCF is the product of the shared factors. HCF = 2 × 3 = 6 d) The LCM is the product of all the factors in the Venn diagram. LCM = 3 × 2 × 3 × 7 = 126

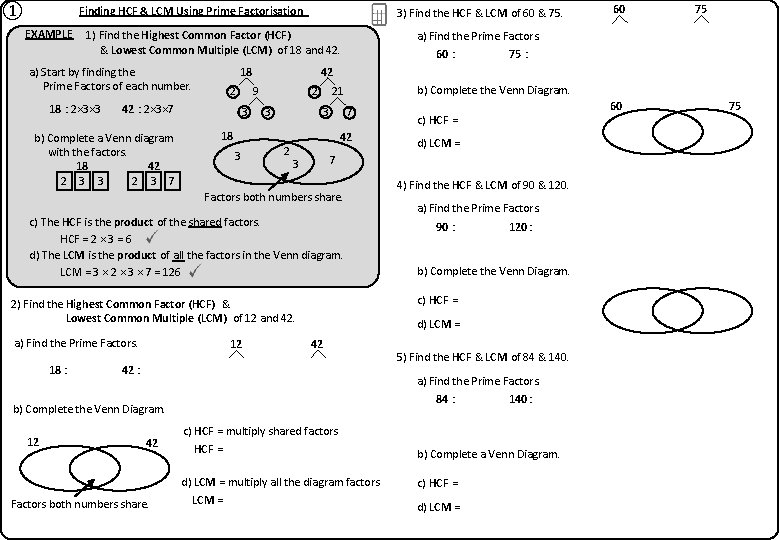
① Finding HCF & LCM Using Prime Factorisation EXAMPLE 3) Find the HCF & LCM of 60 & 75. 1) Find the Highest Common Factor (HCF) & Lowest Common Multiple (LCM) of 18 and 42. a) Start by finding the Prime Factors of each number. 18 : 2× 3× 3 42 : 2× 3× 7 b) Complete a Venn diagram with the factors. 18 42 2 3 7 2 3 3 9 3 a) Find the Prime Factors. 60 : 3 3 7 2 42 c) The HCF is the product of the shared factors. HCF = 2 × 3 = 6 d) The LCM is the product of all the factors in the Venn diagram. LCM = 3 × 2 × 3 × 7 = 126 18 : 4) Find the HCF & LCM of 90 & 120. a) Find the Prime Factors. 90 : 120 : b) Complete the Venn Diagram. d) LCM = 42 42 : 5) Find the HCF & LCM of 84 & 140. a) Find the Prime Factors. 84 : b) Complete the Venn Diagram. 12 d) LCM = c) HCF = 2) Find the Highest Common Factor (HCF) & Lowest Common Multiple (LCM) of 12 and 42. 12 60 c) HCF = 7 3 Factors both numbers share. a) Find the Prime Factors. 75 : b) Complete the Venn Diagram. 21 2 18 3 42 140 : c) HCF = multiply shared factors HCF = d) LCM = multiply all the diagram factors Factors both numbers share. LCM = 75 42 18 2 60 b) Complete a Venn Diagram. c) HCF = d) LCM = 75

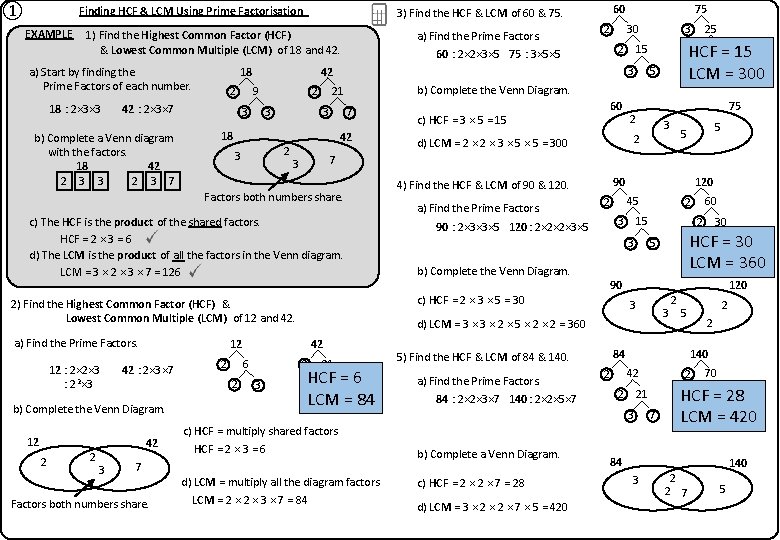
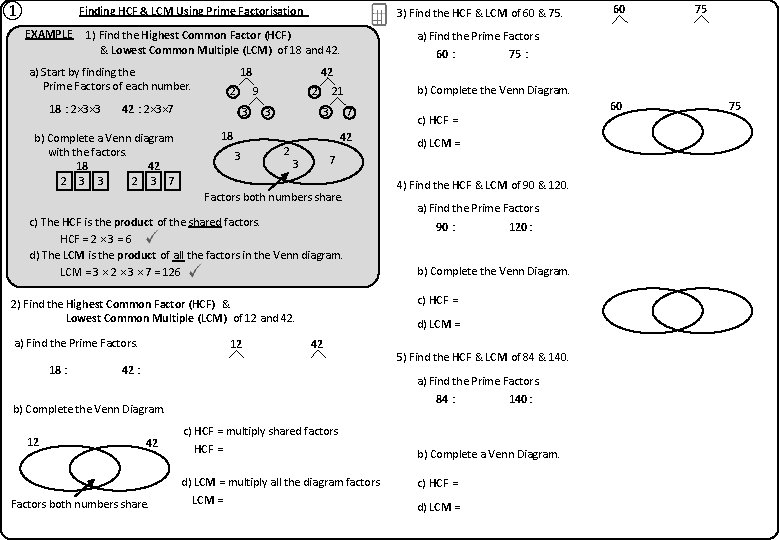
① Finding HCF & LCM Using Prime Factorisation EXAMPLE 1) Find the Highest Common Factor (HCF) & Lowest Common Multiple (LCM) of 18 and 42. a) Start by finding the Prime Factors of each number. 18 : 2× 3× 3 42 : 2× 3× 7 b) Complete a Venn diagram with the factors. 18 42 2 3 7 2 3 3 a) Find the Prime Factors. 9 3 3 3 2 3 b) Complete the Venn Diagram. 7 18 42 c) The HCF is the product of the shared factors. HCF = 2 × 3 = 6 d) The LCM is the product of all the factors in the Venn diagram. LCM = 3 × 2 × 3 × 7 = 126 12 : 2× 2× 3 : 22× 3 42 : 2× 3× 7 2 42 2 3 b) Complete the Venn Diagram. 12 2 2 42 3 21 HCF 3 7= 6 LCM = 84 d) LCM = 2 × 3 × 5 = 300 5 5 90 4) Find the HCF & LCM of 90 & 120. a) Find the Prime Factors. 120 45 2 3 b) Complete the Venn Diagram. 2 84 : 2× 2× 3× 7 140 : 2× 2× 5× 7 HCF = 2 × 3 = 6 d) LCM = multiply all the diagram factors LCM = 2 × 3 × 7 = 84 c) HCF = 2 × 7 = 28 d) LCM = 3 × 2 × 7 × 5 = 420 HCF 2 =1530 LCM 3 = 360 5 5 120 2 3 5 3 84 42 2 140 2 2 21 3 b) Complete a Venn Diagram. 30 90 5) Find the HCF & LCM of 84 & 140. a) Find the Prime Factors. 60 2 3 15 90 : 2× 3× 3× 5 120 : 2× 2× 2× 3× 5 c) HCF = multiply shared factors 7 Factors both numbers share. 3 d) LCM = 3 × 2 × 5 × 2 = 360 12 6 75 2 2 c) HCF = 2 × 3 × 5 = 30 2) Find the Highest Common Factor (HCF) & Lowest Common Multiple (LCM) of 12 and 42. 2 60 c) HCF = 3 × 5 = 15 7 3 Factors both numbers share. a) Find the Prime Factors. 5 5= 15 HCF LCM = 300 5 3 2 15 60 : 2× 2× 3× 5 75 : 3× 5× 5 21 2 75 30 2 42 18 2 60 3) Find the HCF & LCM of 60 & 75. 7 70 2 = 3528 HCF 7 LCM 5 = 420 84 140 3 2 2 7 5

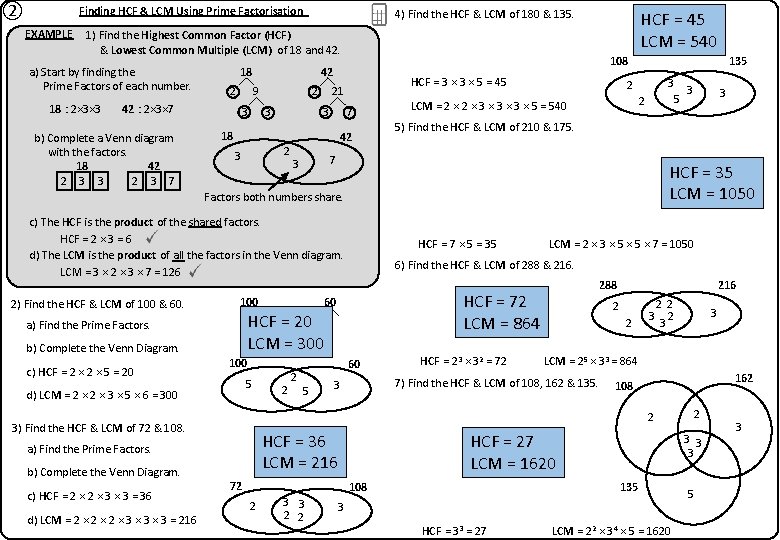
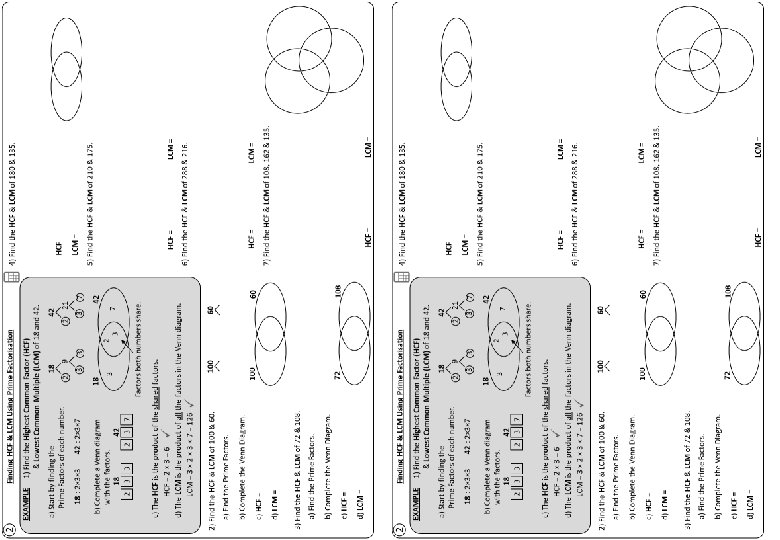
② Finding HCF & LCM Using Prime Factorisation EXAMPLE 4) Find the HCF & LCM of 180 & 135. 1) Find the Highest Common Factor (HCF) & Lowest Common Multiple (LCM) of 18 and 42. a) Start by finding the Prime Factors of each number. 18 : 2× 3× 3 9 2 42 : 2× 3× 7 b) Complete a Venn diagram with the factors. 18 42 2 3 7 2 3 3 108 42 18 3 3 3 7 18 2 3 HCF = 3 × 5 = 45 21 2 HCF = 45 LCM = 540 42 135 3 3 5 2 2 LCM = 2 × 3 × 3 × 5 = 540 5) Find the HCF & LCM of 210 & 175. 7 3 HCF = 35 LCM = 1050 Factors both numbers share. c) The HCF is the product of the shared factors. HCF = 2 × 3 = 6 d) The LCM is the product of all the factors in the Venn diagram. LCM = 3 × 2 × 3 × 7 = 126 2) Find the HCF & LCM of 100 & 60. 100 b) Complete the Venn Diagram. c) HCF = 2 × 5 = 20 5 HCF = 72 LCM = 864 60 5 HCF = 23 × 32 = 72 216 2 2 3 2 2 2 3 72 162 108 HCF = 27 LCM = 1620 2 3 3 2 2 3 HCF = 33 = 27 2 3 3 3 135 108 3 LCM = 25 × 33 = 864 7) Find the HCF & LCM of 108, 162 & 135. 3 HCF = 36 LCM = 216 a) Find the Prime Factors. d) LCM = 2 × 2 × 3 × 3 = 216 2 288 2 3) Find the HCF & LCM of 72 & 108. c) HCF = 2 × 3 × 3 = 36 2 LCM = 2 × 3 × 5 × 7 = 1050 6) Find the HCF & LCM of 288 & 216. 60 100 d) LCM = 2 × 3 × 5 × 6 = 300 b) Complete the Venn Diagram. HCF = 7 × 5 = 35 HCF = 20 LCM = 300 a) Find the Prime Factors. 3 LCM = 22 × 34 × 5 = 1620 5 3

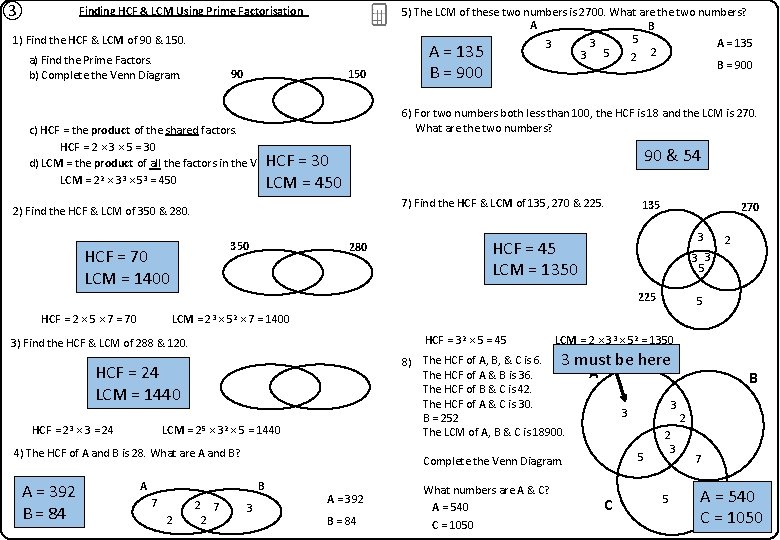
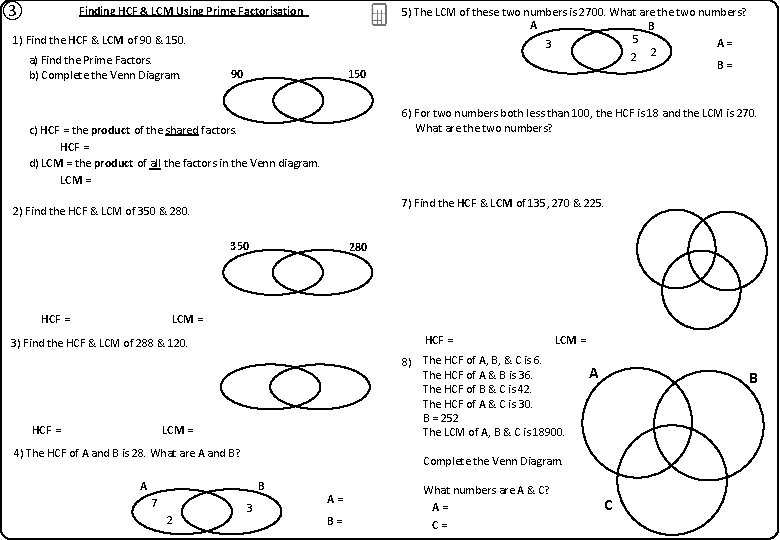
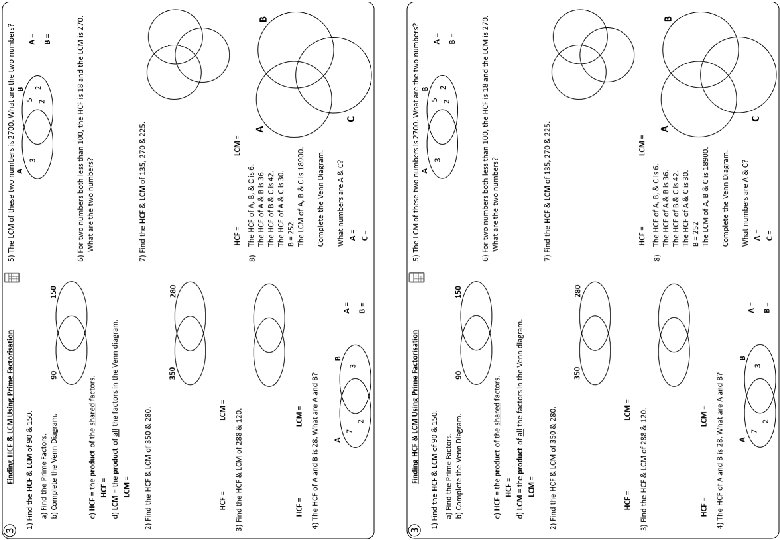
③ Finding HCF & LCM Using Prime Factorisation 1) Find the HCF & LCM of 90 & 150. a) Find the Prime Factors. b) Complete the Venn Diagram. 150 90 5) The LCM of these two numbers is 2700. What are the two numbers? A B 5 3 A = 135 3 2 A = 135 3 5 2 B = 900 6) For two numbers both less than 100, the HCF is 18 and the LCM is 270. What are the two numbers? c) HCF = the product of the shared factors. HCF = 2 × 3 × 5 = 30 HCF = 30 d) LCM = the product of all the factors in the Venn diagram. LCM = 22 × 33 × 53 = 450 LCM = 450 90 & 54 7) Find the HCF & LCM of 135, 270 & 225. 2) Find the HCF & LCM of 350 & 280. 350 HCF = 70 LCM = 1400 280 135 270 3 HCF = 45 LCM = 1350 3 3 5 225 HCF = 2 × 5 × 7 = 70 LCM = 23 × 52 HCF = 32 × 5 = 45 LCM = 25 × 32 × 5 = 1440 4) The HCF of A and B is 28. What are A and B? B 2 2 7 2 must be here A 3 A = 392 B = 84 What numbers are A & C? A = 540 C = 1050 3 3 5 Complete the Venn Diagram. A 7 LCM = 2 × 33 × 52 = 1350 3 8) The HCF of A, B, & C is 6. The HCF of A & B is 36. The HCF of B & C is 42. The HCF of A & C is 30. B = 252 The LCM of A, B & C is 18900. HCF = 24 LCM = 1440 A = 392 B = 84 5 × 7 = 1400 3) Find the HCF & LCM of 288 & 120. HCF = 23 × 3 = 24 2 C 2 3 5 B 2 7 A = 540 C = 1050

① Finding HCF & LCM Using Prime Factorisation EXAMPLE 3) Find the HCF & LCM of 60 & 75. 1) Find the Highest Common Factor (HCF) & Lowest Common Multiple (LCM) of 18 and 42. a) Start by finding the Prime Factors of each number. 18 : 2× 3× 3 42 : 2× 3× 7 b) Complete a Venn diagram with the factors. 18 42 2 3 7 2 3 3 9 3 a) Find the Prime Factors. 60 : 3 3 7 2 42 c) The HCF is the product of the shared factors. HCF = 2 × 3 = 6 d) The LCM is the product of all the factors in the Venn diagram. LCM = 3 × 2 × 3 × 7 = 126 18 : 4) Find the HCF & LCM of 90 & 120. a) Find the Prime Factors. 90 : 120 : b) Complete the Venn Diagram. d) LCM = 42 42 : 5) Find the HCF & LCM of 84 & 140. a) Find the Prime Factors. 84 : b) Complete the Venn Diagram. 12 d) LCM = c) HCF = 2) Find the Highest Common Factor (HCF) & Lowest Common Multiple (LCM) of 12 and 42. 12 60 c) HCF = 7 3 Factors both numbers share. a) Find the Prime Factors. 75 : b) Complete the Venn Diagram. 21 2 18 3 42 140 : c) HCF = multiply shared factors HCF = d) LCM = multiply all the diagram factors Factors both numbers share. LCM = 75 42 18 2 60 b) Complete a Venn Diagram. c) HCF = d) LCM = 75


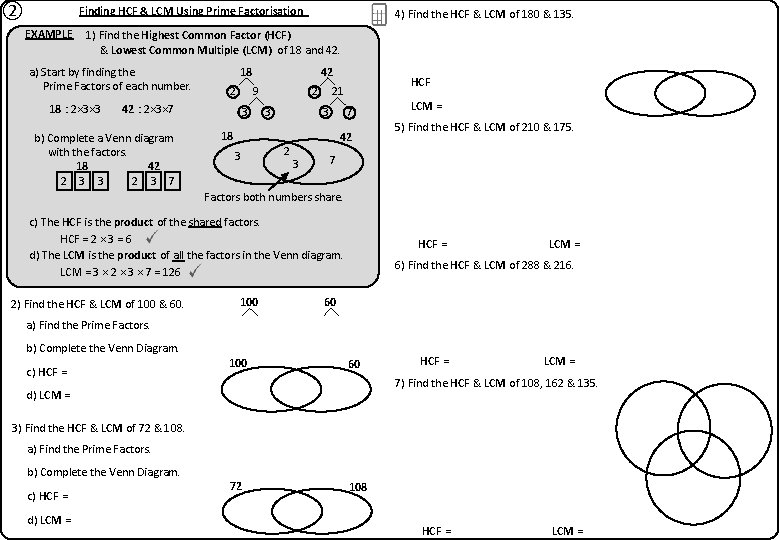
② Finding HCF & LCM Using Prime Factorisation EXAMPLE 4) Find the HCF & LCM of 180 & 135. 1) Find the Highest Common Factor (HCF) & Lowest Common Multiple (LCM) of 18 and 42. a) Start by finding the Prime Factors of each number. 18 : 2× 3× 3 9 2 42 : 2× 3× 7 b) Complete a Venn diagram with the factors. 18 42 2 3 7 2 3 3 42 18 3 3 3 7 18 3 2 HCF 21 2 42 3 LCM = 5) Find the HCF & LCM of 210 & 175. 7 Factors both numbers share. c) The HCF is the product of the shared factors. HCF = 2 × 3 = 6 d) The LCM is the product of all the factors in the Venn diagram. LCM = 3 × 2 × 3 × 7 = 126 2) Find the HCF & LCM of 100 & 60. 100 HCF = LCM = 6) Find the HCF & LCM of 288 & 216. 60 a) Find the Prime Factors. b) Complete the Venn Diagram. c) HCF = 100 60 HCF = LCM = 7) Find the HCF & LCM of 108, 162 & 135. d) LCM = 3) Find the HCF & LCM of 72 & 108. a) Find the Prime Factors. b) Complete the Venn Diagram. c) HCF = d) LCM = 72 108 HCF = LCM =


③ Finding HCF & LCM Using Prime Factorisation 1) Find the HCF & LCM of 90 & 150. a) Find the Prime Factors. b) Complete the Venn Diagram. 150 90 6) For two numbers both less than 100, the HCF is 18 and the LCM is 270. What are the two numbers? c) HCF = the product of the shared factors. HCF = d) LCM = the product of all the factors in the Venn diagram. LCM = 7) Find the HCF & LCM of 135, 270 & 225. 2) Find the HCF & LCM of 350 & 280. 350 HCF = 5) The LCM of these two numbers is 2700. What are the two numbers? A B 5 A= 3 2 2 B= 280 LCM = HCF = 3) Find the HCF & LCM of 288 & 120. HCF = 8) The HCF of A, B, & C is 6. The HCF of A & B is 36. The HCF of B & C is 42. The HCF of A & C is 30. B = 252 The LCM of A, B & C is 18900. LCM = 4) The HCF of A and B is 28. What are A and B? B 2 A B Complete the Venn Diagram. A 7 LCM = 3 A= B= What numbers are A & C? A= C= C


Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk