KS 4 Mathematics N 1 Integers 1 of











































- Slides: 64

KS 4 Mathematics N 1 Integers 1 of 64 © Boardworks Ltd 2005

Contents N 1 Integers A N 1. 1 Classifying numbers A N 1. 2 Calculating with integers A N 1. 3 Multiples, factors and primes A N 1. 4 Prime factor decomposition A N 1. 5 LCM and HCF 2 of 64 © Boardworks Ltd 2005

Classifying numbers Natural numbers Positive whole numbers 0, 1, 2, 3, 4 … Integers Positive and negative whole numbers … – 3, – 2, 1, 0, 1, 2, 3, … Rational numbers Numbers that can be expressed in the form n/m, where n and m are integers. All fractions and all terminating and recurring. decimals are rational numbers, for example, ¾, – 0. 63, 0. 2. Irrational numbers Numbers that cannot be expressed in the form n/m, where n and m are integers. Examples of irrational numbers are and 2. 3 of 64 © Boardworks Ltd 2005

Even numbers are numbers that are exactly divisible by 2. For example, 48 is an even number. It can be written as 48 = 2 × 24. All even numbers end in 0, 2, 4, 6 or 8. Even numbers can be illustrated using dots or counters arranged as follows: E(1) = 2 E(2) = 4 E(3) = 6 E(4) = 8 E(5) = 10 The nth even number can be written as E(n) = 2 n. 4 of 64 © Boardworks Ltd 2005

Odd numbers leave a remainder of 1 when divided by 2. For example, 17 is an odd number. It can be written as 17 = 2 × 8 + 1 All odd numbers end in 1, 3, 5, 7 or 9. Odd numbers can be illustrated using dots or counters arranged as follows: U(1) = 1 U(2) = 3 U(3) = 5 U(4) = 7 U(5) = 9 The nth odd number can be written as U(n) = 2 n – 1. 5 of 64 © Boardworks Ltd 2005

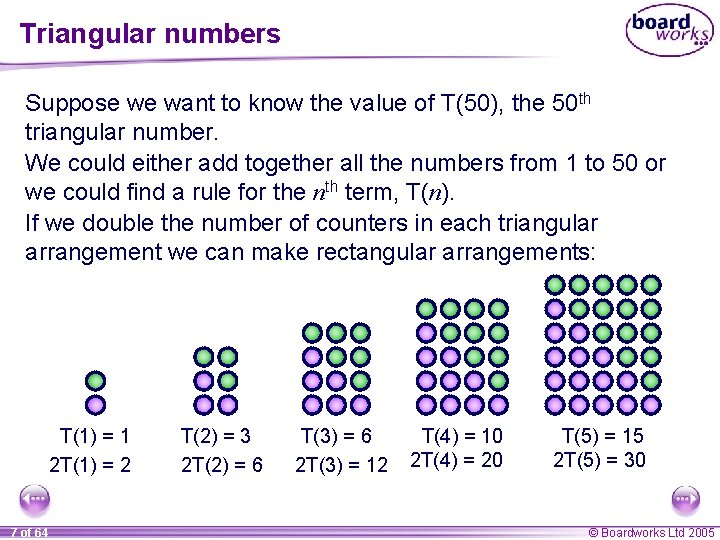
Triangular numbers are numbers that can be written as the sum of consecutive whole numbers starting with 1. For example, 15 is a triangular number. It can be written as 15 = 1 + 2 + 3 + 4 + 5 Triangular numbers can be illustrated using dots or counters arranged in triangles: T(1) = 1 6 of 64 T(2) = 3 T(3) = 6 T(4) = 10 T(5) = 15 © Boardworks Ltd 2005

Triangular numbers Suppose we want to know the value of T(50), the 50 th triangular number. We could either add together all the numbers from 1 to 50 or we could find a rule for the nth term, T(n). If we double the number of counters in each triangular arrangement we can make rectangular arrangements: T(1) = 1 2 T(1) = 2 7 of 64 T(2) = 3 2 T(2) = 6 T(3) = 6 2 T(3) = 12 T(4) = 10 2 T(4) = 20 T(5) = 15 2 T(5) = 30 © Boardworks Ltd 2005

Triangular numbers Any rectangular arrangement of counters can be written as the product of two whole numbers: T(1) = 1 T(2) = 3 T(3) = 6 T(4) = 10 T(5) = 15 2 T(1) = 2 2 T(2) = 6 2 T(3) = 12 2 T(4) = 20 2 T(5) = 30 2 T(1) = 1 × 2 2 T(2) = 2 × 3 2 T(3) = 3 × 4 2 T(4) = 4 × 5 2 T(5) = 5 × 6 From these arrangements we can see that 2 T(n) = n(n + 1) So, for any triangular number T(n) = 8 of 64 n(n + 1) 2 © Boardworks Ltd 2005

Triangular numbers We can now use this rule to find the value of the 50 th triangular number. T(n) = n(n + 1) 2 T(50) = 50(50 + 1) 2 T(50) = 50 × 51 2 T(50) = 2550 2 T(50) = 1275 9 of 64 © Boardworks Ltd 2005

Gauss’ method for adding consecutive numbers There is a story that when the famous mathematician Karl Friedrich Gauss was a young boy at school, his teacher asked the class to add up the numbers from one to a hundred. The teacher expected this activity to keep the class quiet for some time and so he was amazed when Gauss put up his hand gave the answer, 5050, almost immediately! 10 of 64 © Boardworks Ltd 2005

Gauss’ method for adding consecutive numbers Gauss worked the answer out by noticing that you can quickly add together consecutive numbers by writing the numbers once in order and once in reverse order and adding them together. For example, to add the numbers from 1 to 10: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 11 + 11 + 11 + 11 = 110 Sum of the numbers from 1 to 10 = 110 ÷ 2 = 55 Use this method to show that the nth triangular number is: n(n + 1) T(n) = 2 11 of 64 © Boardworks Ltd 2005

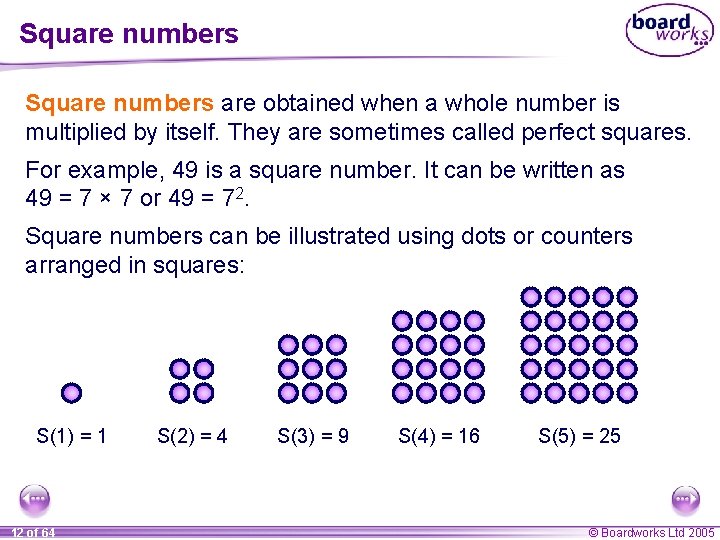
Square numbers are obtained when a whole number is multiplied by itself. They are sometimes called perfect squares. For example, 49 is a square number. It can be written as 49 = 7 × 7 or 49 = 72. Square numbers can be illustrated using dots or counters arranged in squares: S(1) = 1 12 of 64 S(2) = 4 S(3) = 9 S(4) = 16 S(5) = 25 © Boardworks Ltd 2005

Making square numbers The nth square number S(n) can be written as S(n) = n 2. There are several ways to generate a sequence of square numbers. We can multiply a whole number by itself. For example, 25 = 5 × 5 or 25 = 52. We can add consecutive odd numbers starting from 1. For example, 25 = 1 + 3 + 5 + 7 + 9. We can add together two consecutive triangular numbers. For example, 25 = 10 + 15 We can find the product of two consecutive even or odd numbers and add 1. For example, 25 = 4 × 6 + 1. 13 of 64 © Boardworks Ltd 2005

Difference between consecutive squares Show that the difference between two consecutive square numbers is always an odd number. If we use the general form for a square number n 2, where n is a whole number, we can write the square number following it as (n + 1)2. The difference between two consecutive square numbers can therefore be written as (n + 1)2 – n 2 = (n + 1) – n 2 = n 2 + n + 1 – n 2 = 2 n + 1 is always an odd number for any whole number n. 14 of 64 © Boardworks Ltd 2005

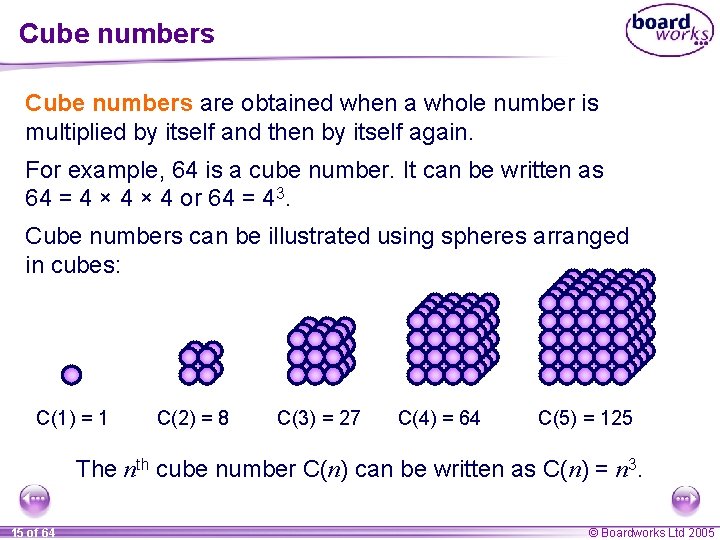
Cube numbers are obtained when a whole number is multiplied by itself and then by itself again. For example, 64 is a cube number. It can be written as 64 = 4 × 4 or 64 = 43. Cube numbers can be illustrated using spheres arranged in cubes: C(1) = 1 C(2) = 8 C(3) = 27 C(4) = 64 C(5) = 125 The nth cube number C(n) can be written as C(n) = n 3. 15 of 64 © Boardworks Ltd 2005

Squares, triangles and primes 16 of 64 © Boardworks Ltd 2005

Contents N 1 Integers A N 1. 1 Classifying numbers A N 1. 2 Calculating with integers A N 1. 3 Multiples, factors and primes A N 1. 4 Prime factor decomposition A N 1. 5 LCM and HCF 17 of 64 © Boardworks Ltd 2005

Negative numbers A positive or negative whole number, including zero, is called an integer. For example, – 3 is an integer. – 3 is read as ‘negative three’. This can also be written as – 3. It is 3 less than 0. 0 – 3 = – 3 Here the ‘–’ sign means minus 3 or subtract 3. Here the ‘–’ sign means negative 3. We say, ‘zero minus three equals negative three’. 18 of 64 © Boardworks Ltd 2005

Integers on a number line Positive and negative integers can be shown on a number line. – 8 – 3 Negative integers Positive integers We can use the number line to compare integers. For example, – 3 > – 8 – 3 ‘is greater than’ – 8 19 of 64 © Boardworks Ltd 2005

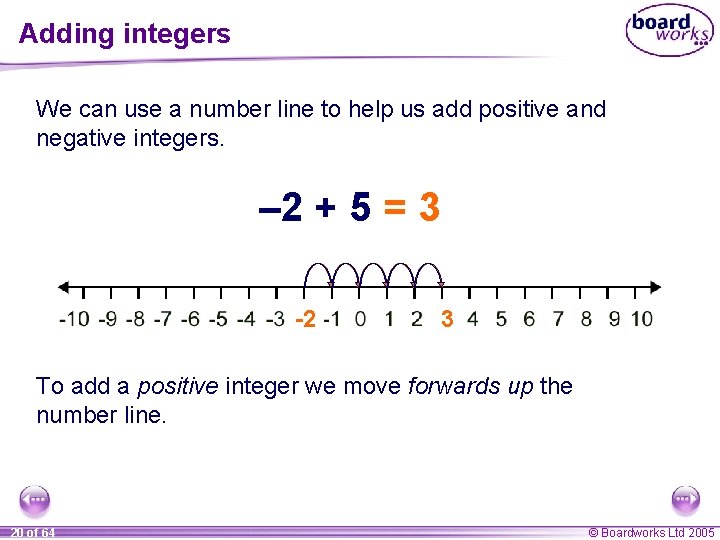
Adding integers We can use a number line to help us add positive and negative integers. – 2 + 5 = 3 -2 3 To add a positive integer we move forwards up the number line. 20 of 64 © Boardworks Ltd 2005

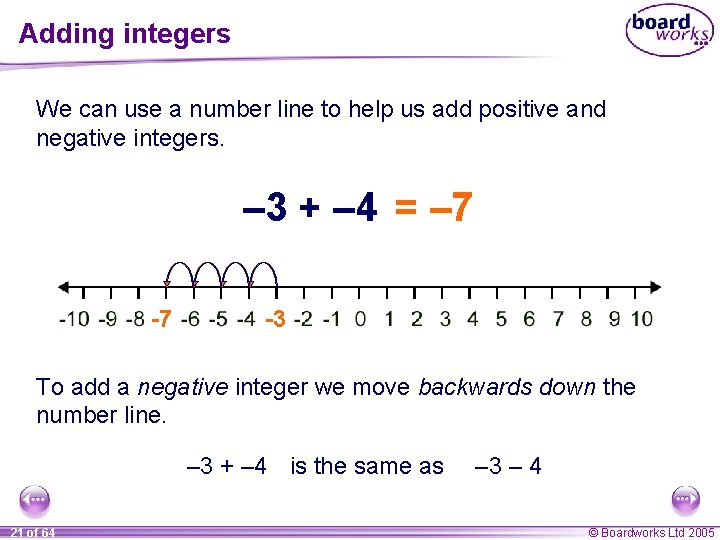
Adding integers We can use a number line to help us add positive and negative integers. – 3 + – 4 == – 7 -7 -3 To add a negative integer we move backwards down the number line. – 3 + – 4 is the same as 21 of 64 – 3 – 4 © Boardworks Ltd 2005

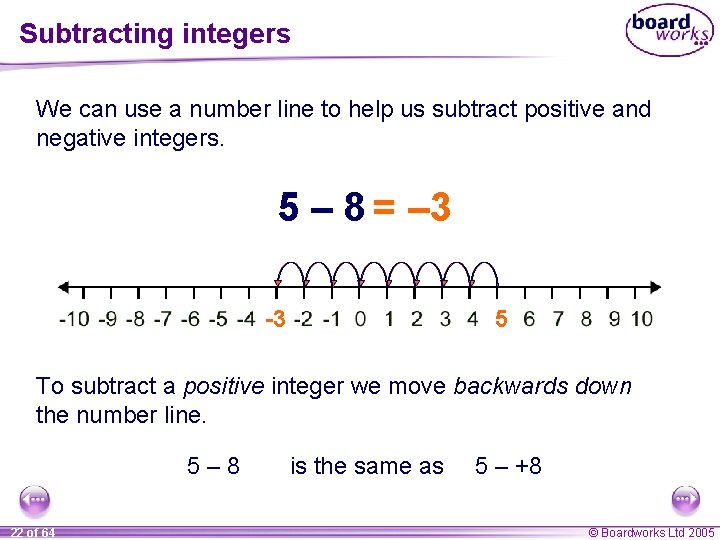
Subtracting integers We can use a number line to help us subtract positive and negative integers. 5 – 8 = – 3 -3 5 To subtract a positive integer we move backwards down the number line. 5– 8 22 of 64 is the same as 5 – +8 © Boardworks Ltd 2005

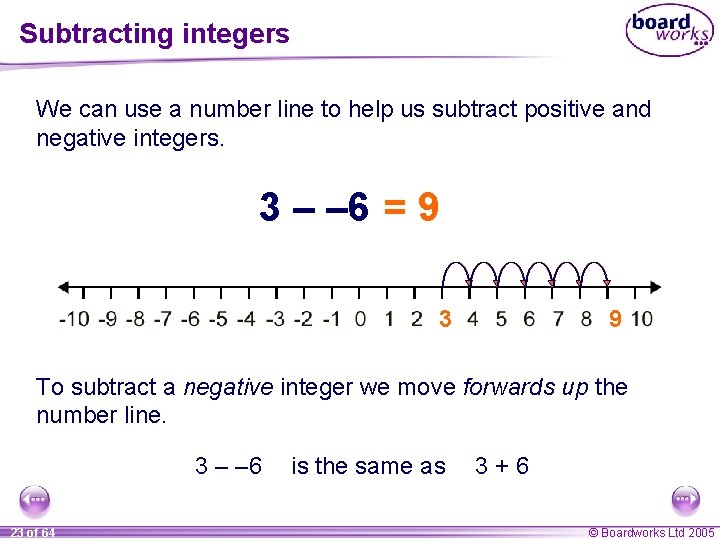
Subtracting integers We can use a number line to help us subtract positive and negative integers. 3 – – 6 = 9 3 9 To subtract a negative integer we move forwards up the number line. 3 – – 6 23 of 64 is the same as 3+6 © Boardworks Ltd 2005

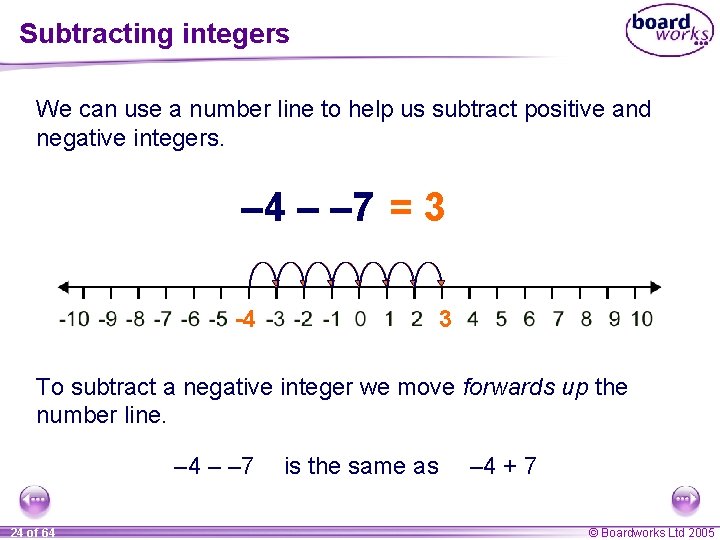
Subtracting integers We can use a number line to help us subtract positive and negative integers. – 4 – – 7 = 3 -4 3 To subtract a negative integer we move forwards up the number line. – 4 – – 7 24 of 64 is the same as – 4 + 7 © Boardworks Ltd 2005

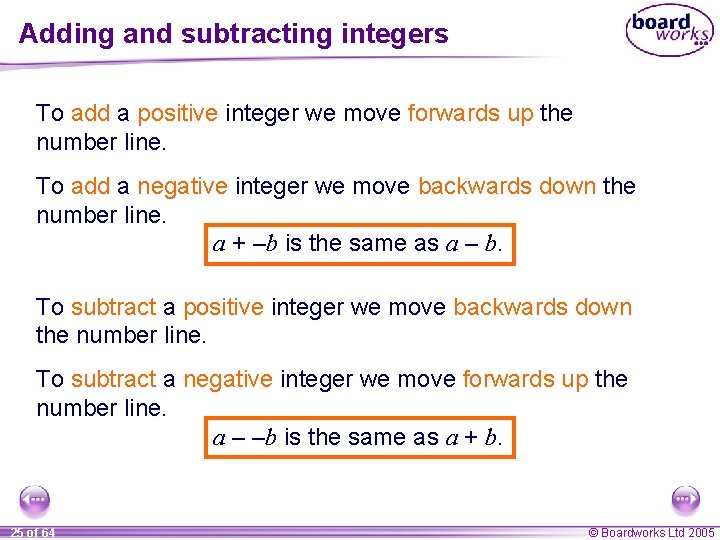
Adding and subtracting integers To add a positive integer we move forwards up the number line. To add a negative integer we move backwards down the number line. a + –b is the same as a – b. To subtract a positive integer we move backwards down the number line. To subtract a negative integer we move forwards up the number line. a – –b is the same as a + b. 25 of 64 © Boardworks Ltd 2005

Integer circle sums 26 of 64 © Boardworks Ltd 2005

Rules for multiplying and dividing When multiplying negative numbers remember: + × + = + + × – = – – × + = – – × – = + Dividing is the inverse operation to multiplying. When we are dividing negative numbers similar rules apply: 27 of 64 + ÷ + = + + ÷ – = – – ÷ + = – – ÷ – = + © Boardworks Ltd 2005

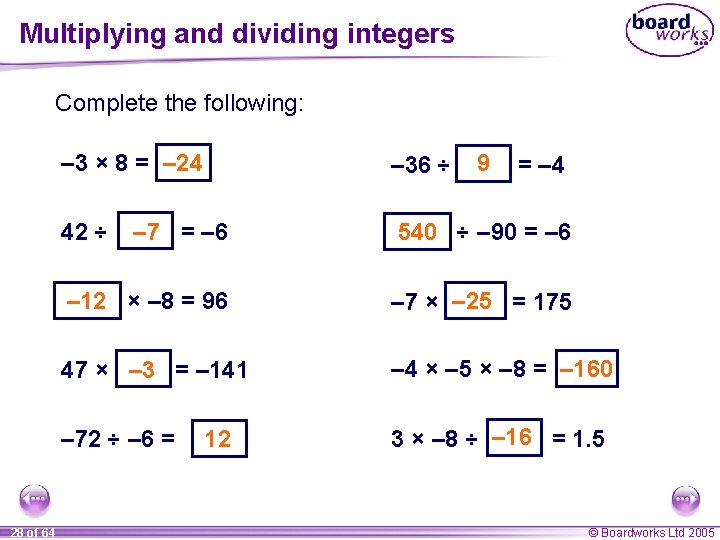
Multiplying and dividing integers Complete the following: 28 of 64 – 3 × 8 = – 24 – 36 ÷ 42 ÷ – 7 = – 6 540 ÷ – 90 = – 6 – 12 × – 8 = 96 – 7 × – 25 = 175 47 × – 3 = – 141 – 4 × – 5 × – 8 = – 160 – 72 ÷ – 6 = 3 × – 8 ÷ – 16 = 1. 5 12 9 = – 4 © Boardworks Ltd 2005

Using a calculator We can enter negative numbers into a calculator by using the sign change key: (–) For example: – 456 ÷ – 6 can be entered as: (–) 4 5 6 ÷ (–) 6 = The answer will be displayed as 76. Always make sure that answers given by a calculator are sensible. 29 of 64 © Boardworks Ltd 2005

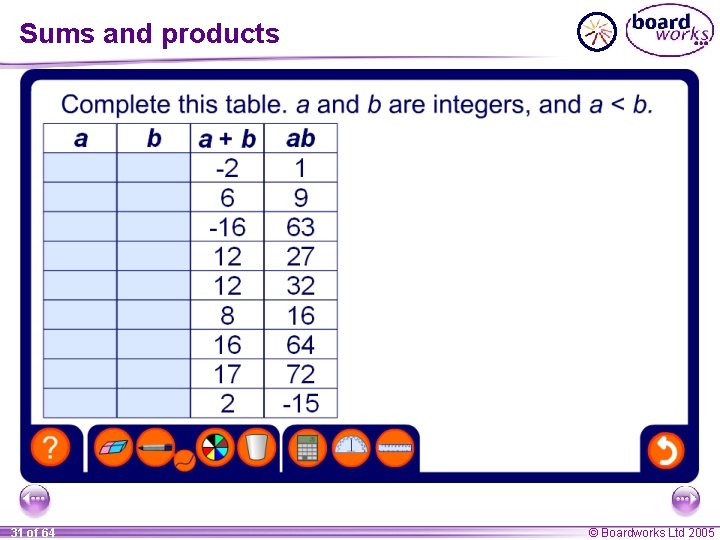
Sums and products What two integers have a sum of 2 and a product of – 8? Start by writing down all of the pairs of numbers that multiply together to make – 8. Since – 8 is negative, one of the numbers must be positive and one of the numbers must be negative. We can have: – 1 × 8 = – 8 – 1 + 8 = 7 1 × – 8 = – 8 1 + – 8 = – 7 – 2 × 4 = – 8 – 2 + 4 = 2 or 2 × – 4 = – 8 2 + – 4 = – 2 The two integers are – 2 and 4. 30 of 64 © Boardworks Ltd 2005

Sums and products 31 of 64 © Boardworks Ltd 2005

Contents N 1 Integers A N 1. 1 Classifying numbers A N 1. 2 Calculating with integers A N 1. 3 Multiples, factors and primes A N 1. 4 Prime factor decomposition A N 1. 5 LCM and HCF 32 of 64 © Boardworks Ltd 2005

Multiples A multiple of a number is found by multiplying the number by any whole number. What are the first six multiples of 7? To find the first six multiples of 7 multiply 7 by 1, 2, 3, 4, 5 and 6 in turn to get: 7, 14, 21, 28, 35 and 42. Any given number has infinitely many multiples. 33 of 64 © Boardworks Ltd 2005

Factors A factor (or divisor) of a number is a whole number that divides into it exactly. Factors come in pairs. For example, What are the factors of 30? 1 and 30, 2 and 15, 3 and 10, 5 and 6. So, in order, the factors of 30 are: 1, 2, 3, 5, 6, 10, 15 and 30. 34 of 64 © Boardworks Ltd 2005

Prime numbers If a whole number has two, and only two, factors it is called a prime number. For example, the number 17 has only two factors, 1 and 17. Therefore, 17 is a prime number. The number 1 has only one factor, 1. Therefore, 1 is not a prime number. There is only one even prime number. What is it? 2 is the only even prime number. 35 of 64 © Boardworks Ltd 2005

Prime numbers There are 25 prime numbers less than 100. These are: 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 What if we go above 100? Around 400 BC the Greek mathematician, Euclid, proved that there are infinitely many prime numbers. 36 of 64 © Boardworks Ltd 2005

Contents N 1 Integers A N 1. 1 Classifying numbers A N 1. 2 Calculating with integers A N 1. 3 Multiples, factors and primes A N 1. 4 Prime factor decomposition A N 1. 5 LCM and HCF 37 of 64 © Boardworks Ltd 2005

Prime factors A prime factor is a factor that is a prime number. For example, What are the prime factors of 70? The factors of 70 are: 1 2 5 7 10 14 35 70 The prime factors of 70 are 2, 5, and 7. 38 of 64 © Boardworks Ltd 2005

Products of prime factors 70 = 2 × 5 × 7 56 = 2 × 2 × 7 This can be written as 56 = 23 × 7 99 = 3 × 11 This can be written as 99 = 32 × 11 Every whole number greater than 1 is either a prime number or can be written as a product of two or more prime numbers. 39 of 64 © Boardworks Ltd 2005

The prime factor decomposition When we write a number as a product of prime factors it is called the prime factor decomposition or prime factor form. For example, The prime factor decomposition of 100 is: 100 = 2 × 5 × 5 = 2 2 × 52 There are two methods of finding the prime factor decomposition of a number. 40 of 64 © Boardworks Ltd 2005

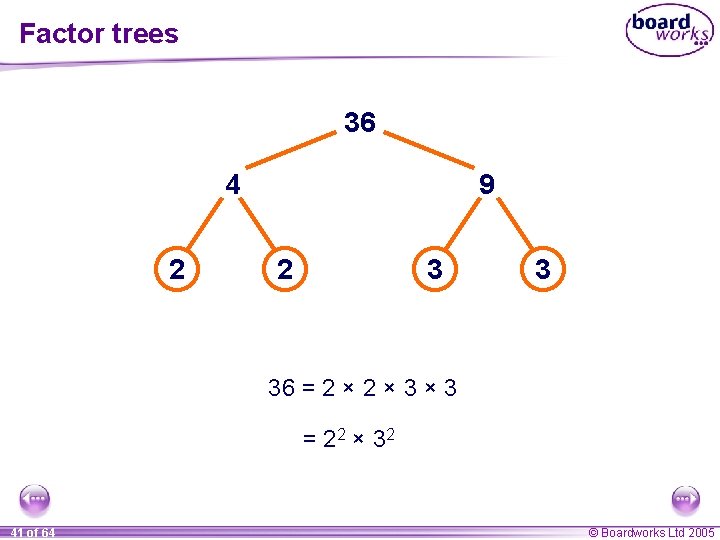
Factor trees 36 4 2 9 2 3 3 36 = 2 × 3 × 3 = 2 2 × 32 41 of 64 © Boardworks Ltd 2005

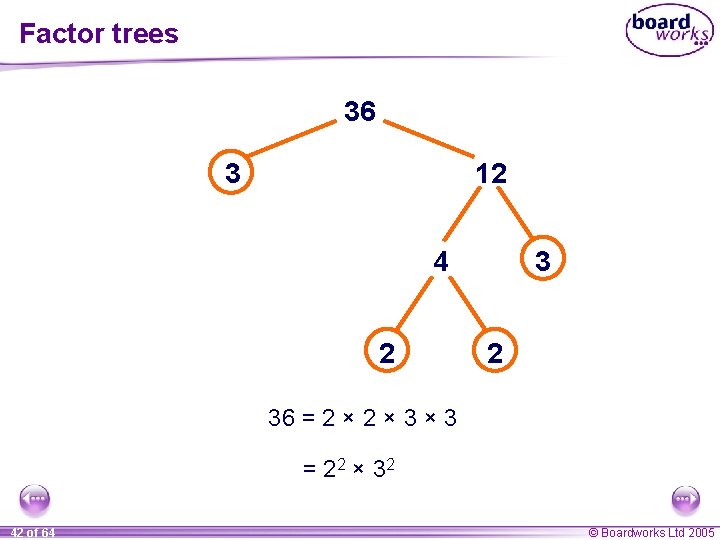
Factor trees 36 3 12 4 2 36 = 2 × 3 × 3 = 2 2 × 32 42 of 64 © Boardworks Ltd 2005

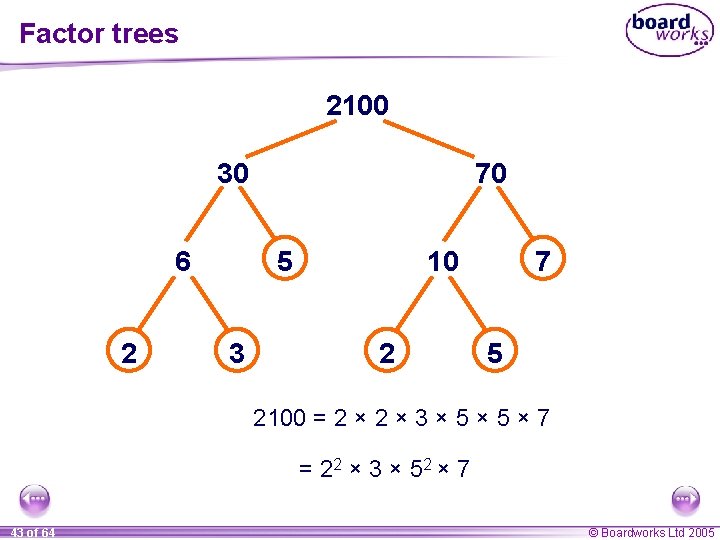
Factor trees 2100 30 6 2 70 5 3 10 2 7 5 2100 = 2 × 3 × 5 × 7 = 2 2 × 3 × 52 × 7 43 of 64 © Boardworks Ltd 2005

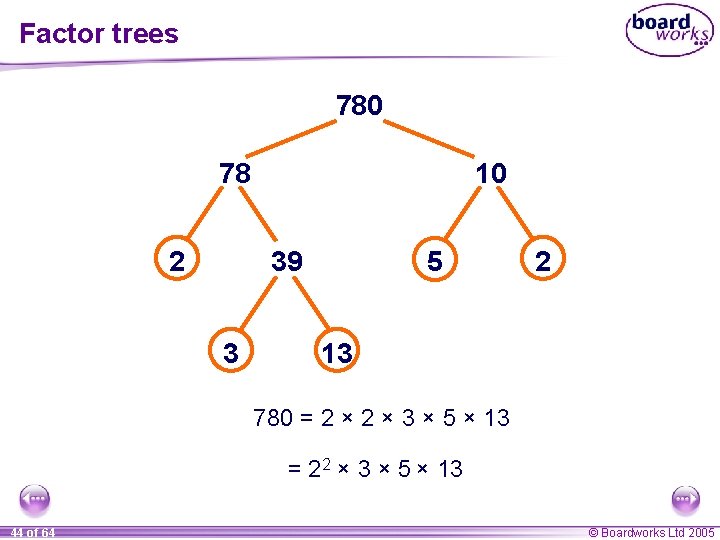
Factor trees 780 78 2 10 39 3 5 2 13 780 = 2 × 3 × 5 × 13 = 22 × 3 × 5 × 13 44 of 64 © Boardworks Ltd 2005

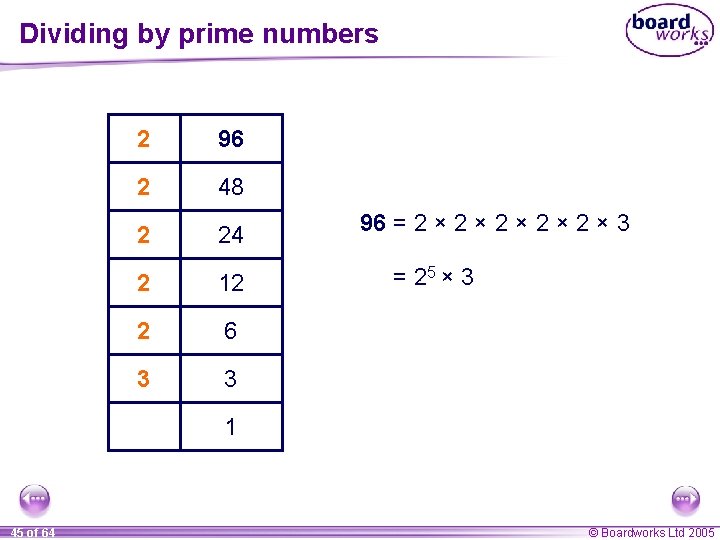
Dividing by prime numbers 2 96 2 48 2 24 2 12 2 6 3 3 96 = 2 × 2 × 2 × 3 = 25 × 3 1 45 of 64 © Boardworks Ltd 2005

Dividing by prime numbers 3 315 3 105 315 = 3 × 5 × 7 5 35 = 32 × 5 × 7 7 7 1 46 of 64 © Boardworks Ltd 2005

Dividing by prime numbers 2 702 3 351 3 117 3 39 13 13 702 = 2 × 3 × 3 × 13 = 2 × 33 × 13 1 47 of 64 © Boardworks Ltd 2005

Using the prime factor decomposition Use the prime factor form of 324 to show that it is a square number. 2 324 2 162 3 81 3 = 2 2 × 34 This can be written as: (2 × 32) × (2 × 32) 27 3 9 3 3 1 48 of 64 324 = 2 × 3 × 3 × 3 or (2 × 32)2 If all the indices in the prime factor decomposition of a number are even, then the number is a square number. © Boardworks Ltd 2005

Using the prime factor decomposition Use the prime factor form of 3375 to show that it is a cube number. 3 3375 3 1125 3 375 5 125 5 5 1 49 of 64 3375 = 3 × 3 × 5 × 5 = 3 3 × 53 This can be written as: (3 × 5) × (3 × 5) or (3 × 5)3 If all the indices in the prime factor decomposition of a number are multiples of 3, then the number is a cube number. © Boardworks Ltd 2005

Using the prime factor decomposition 168 = 23 × 7 4116 = 22 × 3 × 73 294 = 2 × 3 × 72 Use the prime factor decompositions of the numbers given above to answer the following questions. 1) What is 168 × 294 as a product of prime factors? 168 × 294 = (23 × 7) × (2 × 3 × 72 ) = 23 × 2 × 3 × 7 2 = 24 × 3 2 × 7 3 50 of 64 © Boardworks Ltd 2005

Using the prime factor decomposition 168 = 23 × 7 4116 = 22 × 3 × 73 294 = 2 × 3 × 72 Use the prime factor decompositions of the numbers given above to answer the following questions. 2) What is 4116 ÷ 294? 22 × 3 × 7 3 4116 ÷ 294 = 2 × 3 × 72 2× 2× 3× 7× 7× 7 = 2× 3× 7× 7 =2× 7 = 14 51 of 64 © Boardworks Ltd 2005

Using the prime factor decomposition 168 = 23 × 7 4116 = 22 × 3 × 73 294 = 2 × 3 × 72 Use the prime factor decompositions of the numbers given above to answer the following questions. 3) Is 4116 divisible by 168? If we divide 4116 by 168 we have: 22 × 3 × 7 3 4116 ÷ 168 = 23 × 7 2× 2× 3× 7× 7× 7 = 2× 2× 2× 3× 7 There is a 2 left in the denominator No, 4116 is not divisible by 168. 52 of 64 © Boardworks Ltd 2005

Using the prime factor decomposition 168 = 23 × 7 4116 = 22 × 3 × 73 294 = 2 × 3 × 72 Use the prime factor decompositions of the numbers given above to answer the following questions. 4) Show that 294 × 6 is a square number. We can write 6 as 2 × 3 294 × 6 = 2 × 3 × 72 × 3 Rearranging, 294 × 6 = 2 × 3 × 72 = 22 × 3 2 × 7 2 = (2 × 3 × 7)2 53 of 64 © Boardworks Ltd 2005

Using the prime factor decomposition 4116 = 22 × 3 × 73 168 = 23 × 7 294 = 2 × 3 × 72 Use the prime factor decompositions of the numbers given above to answer the following questions. 5) Write the fraction 168 in its simplest form. 294 23 × 7 168 = 2 × 3 × 72 294 2× 2× 2× 3× 7 = 2 × 3 × 7× 7 = 54 of 64 4 7 © Boardworks Ltd 2005

Contents N 1 Integers A N 1. 1 Classifying numbers A N 1. 2 Calculating with integers A N 1. 3 Multiples, factors and primes A N 1. 4 Prime factor decomposition A N 1. 5 LCM and HCF 55 of 64 © Boardworks Ltd 2005

The lowest common multiple (or LCM) of two numbers is the smallest number that is a multiple of both the numbers. For small numbers we can find this by writing down the first few multiples for both numbers until we find a number that is in both lists. For example, Multiples of 20 are : 20, 40, 60, 80, 100, Multiples of 25 are : 25, 50, 75, 100, 125, . . . 120, . . . The LCM of 20 and 25 is 100. 56 of 64 © Boardworks Ltd 2005

The lowest common multiple We use the lowest common multiple when adding and subtracting fractions. For example, Add together 4 9 and 5 12 The LCM of 9 and 12 is 36. 4 9 + × 4 × 3 5 16 12 × 4 57 of 64 = 36 + 15 36 = 31 36 × 3 © Boardworks Ltd 2005

The highest common factor (or HCF) of two numbers is the highest number that is a factor of both numbers. We can find the highest common factor of two numbers by writing down all their factors and finding the largest factor in both lists. For example, Factors of 36 are : 1, 2, 3, 4, 6, Factors of 45 are : 1, 3, 5, 9, 12, 18, 36. 45. The HCF of 36 and 45 is 9. 58 of 64 © Boardworks Ltd 2005

The highest common factor We use the highest common factor when cancelling fractions. For example, Cancel the fraction 36 48 The HCF of 36 and 48 is 12, so we need to divide the numerator and the denominator by 12. ÷ 12 36 48 = 3 4 ÷ 12 59 of 64 © Boardworks Ltd 2005

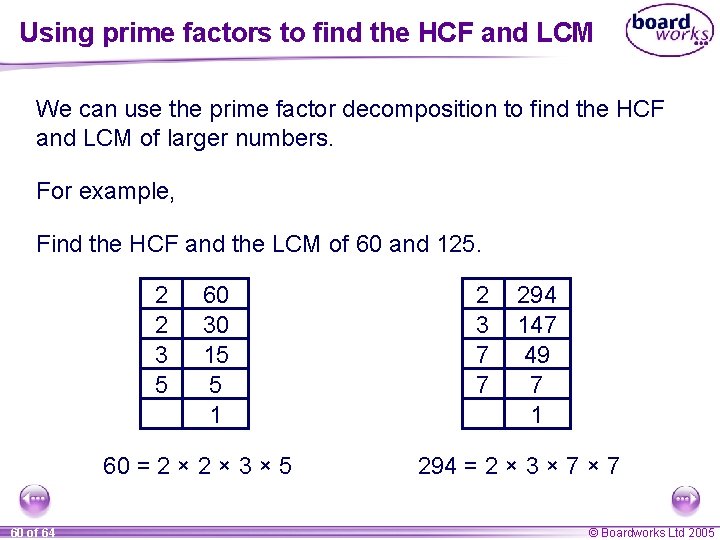
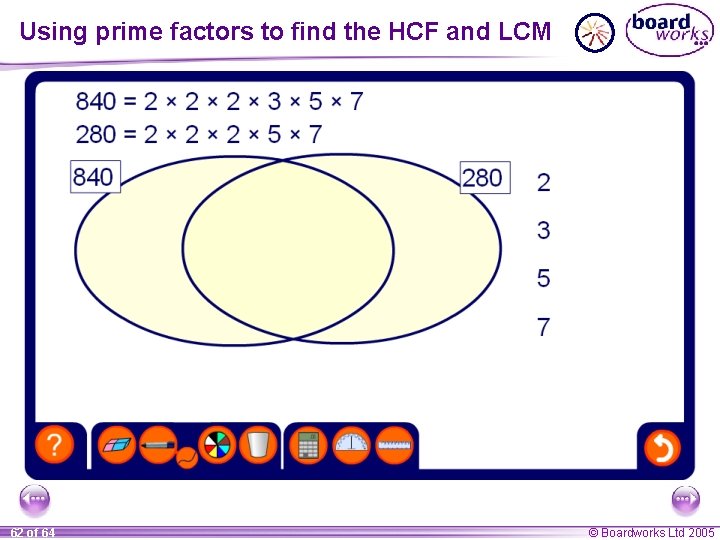
Using prime factors to find the HCF and LCM We can use the prime factor decomposition to find the HCF and LCM of larger numbers. For example, Find the HCF and the LCM of 60 and 125. 2 2 3 5 60 30 15 5 1 60 = 2 × 3 × 5 60 of 64 2 3 7 7 294 147 49 7 1 294 = 2 × 3 × 7 © Boardworks Ltd 2005

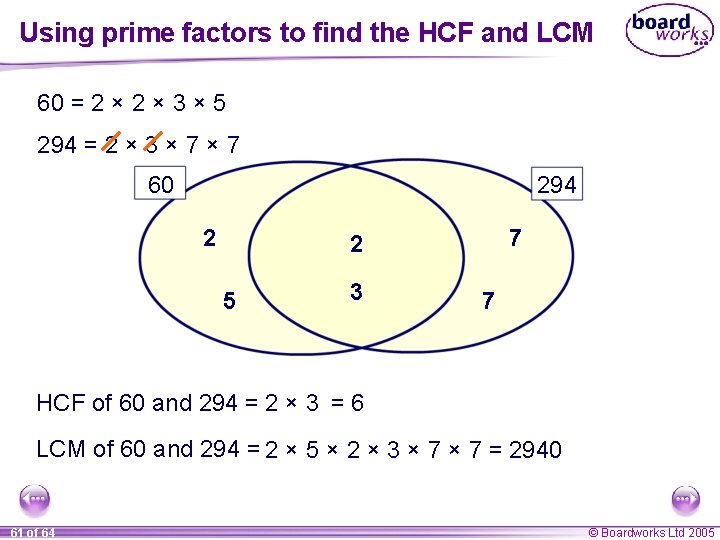
Using prime factors to find the HCF and LCM 60 = 2 × 3 × 5 294 = 2 × 3 × 7 60 294 2 7 2 5 3 7 HCF of 60 and 294 = 2 × 3 = 6 LCM of 60 and 294 = 2 × 5 × 2 × 3 × 7 = 2940 61 of 64 © Boardworks Ltd 2005

Using prime factors to find the HCF and LCM 62 of 64 © Boardworks Ltd 2005

The LCM of co-prime numbers If two numbers have a highest common factor (or HCF) of 1 then they are called co-prime or relatively prime numbers. For two whole numbers a and b we can write: a and b are co-prime if HCF(a, b) = 1 If two whole numbers a and b are co-prime then: LCM(a, b) = ab For example, the numbers 8 and 9 do not share any common multiples other than 1. They are co-prime. Therefore, 63 of 64 LCM(8, 9) = 8 × 9 = 72 © Boardworks Ltd 2005

The LCM of numbers that are not co-prime If two numbers are not co-prime then their highest common factor is greater than 1. If two numbers a and b are not co-prime then their lowest common multiple is equal to the product of the two numbers divided by their highest common factor. We can write this as: LCM(a, b) = ab HCF(a, b) For example, 8 × 12 96 LCM(8, 12) = = 24 = HCF(8, 12) 4 64 of 64 © Boardworks Ltd 2005