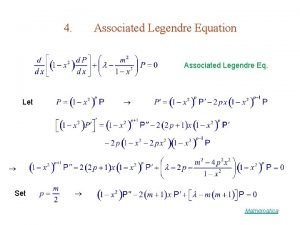The Use of Mathematica in Control Engineering Neil



![tf = Transfer. Function[s, {{1/(s-a), 1/(s-b)}}] tf = Transfer. Function[s, {{1/(s-a), 1/(s-b)}}]](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-4.jpg)

![tfsys = Transfer. Function[s, {{((s+2)(s+3))/(s+1)^2, 1/(s+1)^2}, {(s+2)/(s+1)^2, (s+1)/((s+1)^2(s+3))}, {1/(s+2), 1/(s+1)}}] which now yields tfsys = Transfer. Function[s, {{((s+2)(s+3))/(s+1)^2, 1/(s+1)^2}, {(s+2)/(s+1)^2, (s+1)/((s+1)^2(s+3))}, {1/(s+2), 1/(s+1)}}] which now yields](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-6.jpg)




![Linear Model Transformations G(s) [A, B, C, D] G(s) System Matrix P(s) in polynomial Linear Model Transformations G(s) [A, B, C, D] G(s) System Matrix P(s) in polynomial](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-11.jpg)

![New Data Transformations tfsys = Transfer. Function[s, {{(s+1)/(s^2+2 s+1)}, {(s+2)/(s+1)}}] ps = System. Matrix[tfsys, New Data Transformations tfsys = Transfer. Function[s, {{(s+1)/(s^2+2 s+1)}, {(s+2)/(s+1)}}] ps = System. Matrix[tfsys,](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-13.jpg)
![New Data Transformations tfsys =Transfer. Function[s, {{(s+1)/(s^2+2 s+1)}, {(s+2)/(s+1)}] rff = Right. Matrix. Fraction[tfsys] New Data Transformations tfsys =Transfer. Function[s, {{(s+1)/(s^2+2 s+1)}, {(s+2)/(s+1)}] rff = Right. Matrix. Fraction[tfsys]](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-14.jpg)
![New Data Transformations Right. Matrix. Fraction[%] System. Matrix[dt, Target. Form->Right. Fraction] System. Matrix[dt] New Data Transformations Right. Matrix. Fraction[%] System. Matrix[dt, Target. Form->Right. Fraction] System. Matrix[dt]](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-15.jpg)


![System Analysis Controllable[ss] Observable[ss] ss =[A, B, C, D] Controllable[ps] Observable[ps] Smith. Form[T(s) U(s)] System Analysis Controllable[ss] Observable[ss] ss =[A, B, C, D] Controllable[ps] Observable[ps] Smith. Form[T(s) U(s)]](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-18.jpg)



![Preliminary Analysis Application of the decoupling zeros algorithm to [s. I-A, B] yielded Dimensions Preliminary Analysis Application of the decoupling zeros algorithm to [s. I-A, B] yielded Dimensions](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-23.jpg)





![Ackermann’s Formula Here is the controllability matrix of [A, b], and pc(s) is the Ackermann’s Formula Here is the controllability matrix of [A, b], and pc(s) is the](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-30.jpg)









![Preliminary Analysis Application of the decoupling zeros algorithm to [s. I-A, B] yielded Dimensions Preliminary Analysis Application of the decoupling zeros algorithm to [s. I-A, B] yielded Dimensions](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-56.jpg)




- Slides: 68

The Use of Mathematica in Control Engineering Neil Munro Control Systems Centre UMIST Manchester, England. • Linear Model Descriptions • Linear Model Transformations • Linear System Analysis Tools • Design/Synthesis Techniques • Pole Assignment • Model-Reference Optimal Control • PID Controller • Concluding Remarks

Linear Model Descriptions The Control System Professional currently provides several ways of describing linear system models; e. g. 1 For systems described by the state-space equations where y is a vector of the system outputs u is a vector of the system inputs and 2 x is a vector of the system state-variables For systems described by transfer-function relationships where s is the complex variable

Examples: - ss = State. Space[{{0, 0, 1, 0}, {0, 0, 0, 1}, {-(a b), 0, a+b, 0}, {0, -(a b), 0, a+b}}, {{0, 0}, {1, 0}, {0, 1}}, {{-b, -a, 1, 1}}]
![tf Transfer Functions 1sa 1sb tf = Transfer. Function[s, {{1/(s-a), 1/(s-b)}}]](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-4.jpg)
tf = Transfer. Function[s, {{1/(s-a), 1/(s-b)}}]

New Data Formats have been implemented, for these objects, which are fully editable, as follows: ss = State. Space[{{0, 0, 1, 0}, {0, 0, 0, 1}, {-(a b), 0, a+b, 0}, {0, -(a b), 0, a+b}}, {{0, 0}, {1, 0}, {0, 1}}, {{-b, -a, 1, 1}}] now results in the composite data matrix
![tfsys Transfer Functions s2s3s12 1s12 s2s12 s1s12s3 1s2 1s1 which now yields tfsys = Transfer. Function[s, {{((s+2)(s+3))/(s+1)^2, 1/(s+1)^2}, {(s+2)/(s+1)^2, (s+1)/((s+1)^2(s+3))}, {1/(s+2), 1/(s+1)}}] which now yields](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-6.jpg)
tfsys = Transfer. Function[s, {{((s+2)(s+3))/(s+1)^2, 1/(s+1)^2}, {(s+2)/(s+1)^2, (s+1)/((s+1)^2(s+3))}, {1/(s+2), 1/(s+1)}}] which now yields

New Data Objects Four new data objects have been introduced; namely, 1. Rosenbrock’s system matrix in polynomial form 2. Rosenbrock’s system matrix in statespace form 3. The right matrix-fraction description of a system 4. The left matrix-fraction description of a system.

The system matrix in polynomial form provides a compact description of a linear dynamical system described by arbitrary ordered differential equations and algebraic relationships, after the application of the Laplace transform with zero initial conditions; namely where , u and y are vectors of the Laplace transformed system variables. This set of equations can equally be written as

The system matrix in polynomial form is then defined as When a system matrix in polynomial form is being created, it is important to note that the dimension of the square matrix T(s) must be adjusted to be r, where r is the degree of Det[T(s)]. If the system description is known in statespace form then a special form of the system matrix can be constructed, known as the system matrix in state-space form, as shown below

Matrix Fraction Forms Given a system description in transfer function matrix form G(s), for certain analysis and design purposes; e. g. the H- approach to robust control system design; it is often convenient to express this model in the form of a left or right matrixfraction description; e. g. 1. A left matrix-fraction form of a given transfer function matrix G(s) might be 2 A right matrix fraction form of a given transfer function matrix G(s) might be
![Linear Model Transformations Gs A B C D Gs System Matrix Ps in polynomial Linear Model Transformations G(s) [A, B, C, D] G(s) System Matrix P(s) in polynomial](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-11.jpg)
Linear Model Transformations G(s) [A, B, C, D] G(s) System Matrix P(s) in polynomial form [A, B, C, D] System Matrix P(s) in state-space form [T(s), U(s), V(s), W(s)] System Matrix P(s) in polynomial form Least Order P 1(s) P 2(s)

New Data Transformations All data formats are fully editable tfsys = Transfer. Function[s, {{((s+2)(s+3))/(s+1)^2, 1/(s+1)^2}, {(s+2)/(s+1)^2, (s+1)/((s+1)^2(s+3))}, {1/(s+2), 1/(s+1)}}] ss = State. Space[tfsys] rff = Right. Matrix. Fraction[ss, s]
![New Data Transformations tfsys Transfer Functions s1s22 s1 s2s1 ps System Matrixtfsys New Data Transformations tfsys = Transfer. Function[s, {{(s+1)/(s^2+2 s+1)}, {(s+2)/(s+1)}}] ps = System. Matrix[tfsys,](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-13.jpg)
New Data Transformations tfsys = Transfer. Function[s, {{(s+1)/(s^2+2 s+1)}, {(s+2)/(s+1)}}] ps = System. Matrix[tfsys, Target. Form Right. Fraction] rff = Right. Matrix. Fraction[ps] Transfer. Function[%] ps = System. Matrix[tfsys, Target. Form Left. Fraction] lf = Left. Fraction. Form[ ]
![New Data Transformations tfsys Transfer Functions s1s22 s1 s2s1 rff Right Matrix Fractiontfsys New Data Transformations tfsys =Transfer. Function[s, {{(s+1)/(s^2+2 s+1)}, {(s+2)/(s+1)}] rff = Right. Matrix. Fraction[tfsys]](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-14.jpg)
New Data Transformations tfsys =Transfer. Function[s, {{(s+1)/(s^2+2 s+1)}, {(s+2)/(s+1)}] rff = Right. Matrix. Fraction[tfsys] dt = To. Discrete. Time[tfsys, Sampled->20]//Simplify
![New Data Transformations Right Matrix Fraction System Matrixdt Target FormRight Fraction System Matrixdt New Data Transformations Right. Matrix. Fraction[%] System. Matrix[dt, Target. Form->Right. Fraction] System. Matrix[dt]](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-15.jpg)
New Data Transformations Right. Matrix. Fraction[%] System. Matrix[dt, Target. Form->Right. Fraction] System. Matrix[dt]

A Least-Order form of a System-Matrix in polynomial form is one in which there are no input-decoupling zeros and no outputdecoupling zeros, and would yield a minimal state-space realization, when directly converted to state-space form. For example, the polynomial system matrix is not least order, since T(s) and U(s) have 3 input-decoupling zeros at s = {0, 0, -1}; i. e. [T(s) U(s)] has rank 4 at these values of s.

Hence
![System Analysis Controllabless Observabless ss A B C D Controllableps Observableps Smith FormTs Us System Analysis Controllable[ss] Observable[ss] ss =[A, B, C, D] Controllable[ps] Observable[ps] Smith. Form[T(s) U(s)]](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-18.jpg)
System Analysis Controllable[ss] Observable[ss] ss =[A, B, C, D] Controllable[ps] Observable[ps] Smith. Form[T(s) U(s)] Mc. Millan. Form[G(s)] Decoupling Zeros Matrix. Left. GCD[T(s) U(s)] Matrix. Right. GCD[T(s) V(s)]

Controllability and Observability In the same way that the controllability and observability of a system described by a set of state space equations can be determined in the Control System Professional by entering the commands Controllable[ss] and Observable[ss] where ss is a State. Space object. These tests can now also be directly applied to a system matrix object by entering the commands Controllable[sm] and Observable[sm] where sm is a System. Matrix object in either polynomial form or state space form.

Preliminary Analysis • Reduction of State-Space Equations • Given a system matrix in state-space form • then an input-decoupling zeros algorithm, • implemented in Mathematica, reduces P(s) to • The completely controllable part is then given by

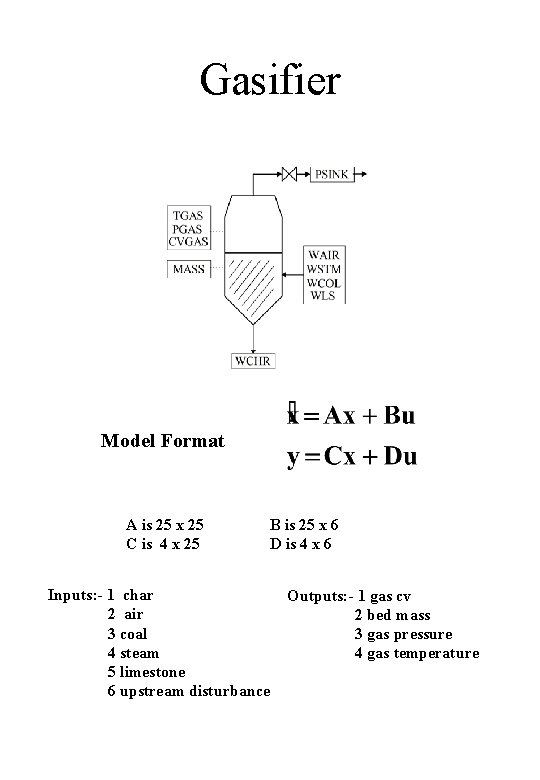
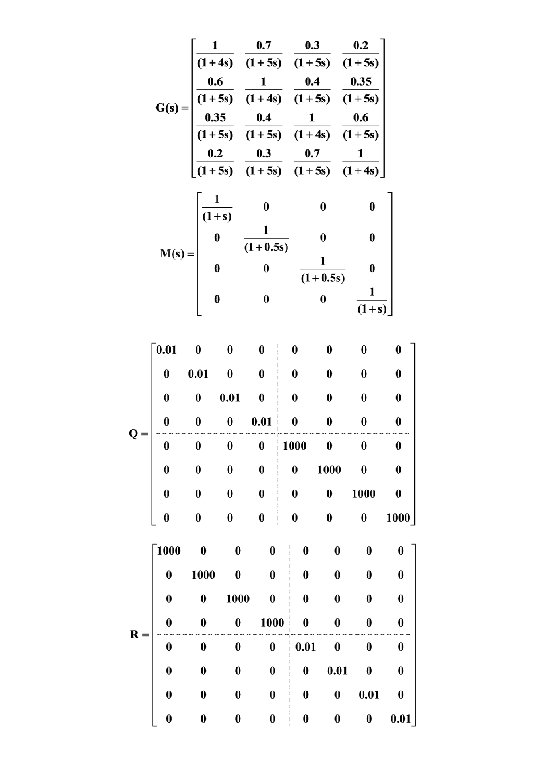
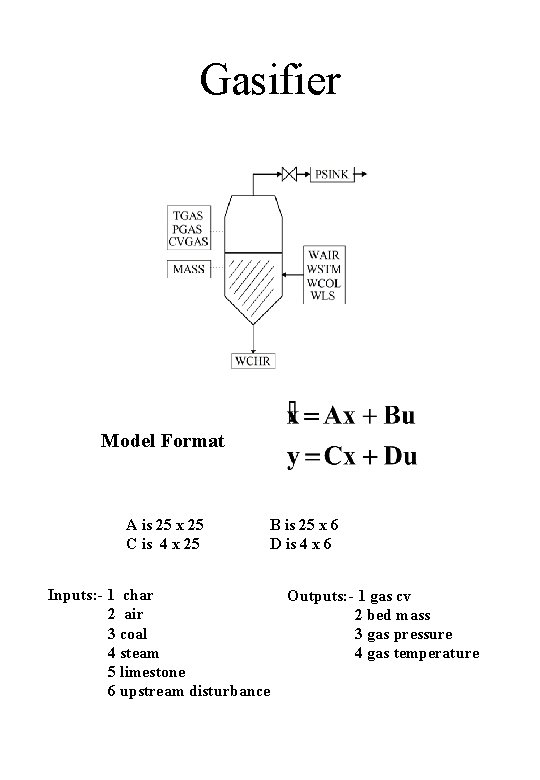
Gasifier Model Format A is 25 x 25 C is 4 x 25 Inputs: - 1 char 2 air 3 coal 4 steam 5 limestone 6 upstream disturbance B is 25 x 6 D is 4 x 6 Outputs: - 1 gas cv 2 bed mass 3 gas pressure 4 gas temperature

Preliminary Analysis The original 25 th order system is numerically very ill conditioned. The eigenvalues cover a significant range in the complex plane, ranging from -0. 00033 to -33. 1252. The condition number is 5. 24 x 1019. At w = 0 the maximum and minimum singular values are 147500 and 50, respectively. The Kalman controllability and observability tests yield a rank of 1, and the controllability and observability gramians are : -
![Preliminary Analysis Application of the decoupling zeros algorithm to s IA B yielded Dimensions Preliminary Analysis Application of the decoupling zeros algorithm to [s. I-A, B] yielded Dimensions](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-23.jpg)
Preliminary Analysis Application of the decoupling zeros algorithm to [s. I-A, B] yielded Dimensions of indicating that the system had 7 input-decoupling zeros, which was confirmed by transforming A and B to spectral form.

Coprime Factorizations

Smith and Mc. Millan Forms The Smith form of a polynomial matrix and the Mc. Millan form of a rational polynomial matrix are both important in control systems analysis. Consider an x m polynomial matrix N(s), then the Smith form of N(s) is defined as S(s) = L(s)N(s)R(s) and L(s) and R(s) are unimodular matrices.

Smith and Mc. Millan Forms Consider now an x m rational polynomial matrix G(s), and let G(s) = N(s)/d(s) where d(s) is the monic least common denominator of G(s), then the Mc. Millan form of G(s) is defined as where M(s) is the result of dividing the Smith form of N(s) by d(s), and cancelling out all common factors

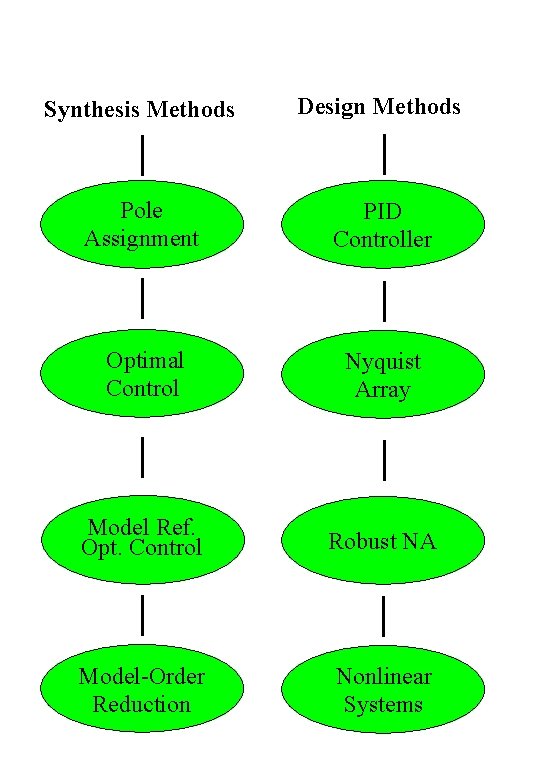
Synthesis Methods Design Methods Pole Assignment PID Controller Optimal Control Nyquist Array Model Ref. Opt. Control Robust NA Model-Order Reduction Nonlinear Systems

Design/Synthesis Methods implemented are: 1 Pole Assignment - Some Observations 2 Model-Reference Optimal Control 3 The Systematic Design of PID Controllers 4 Uncertain Nonlinear Systems 5 Robust Direct Nyquist Array Design Method 6 Model-Order Reduction

Pole Assignment We consider four main types of approaches • ACKERMANN’S FORMULA • SPECTRAL APPROACH • MAPPING APPROACH • EIGENVECTOR METHODS Control Systems Centre - UMIST
![Ackermanns Formula Here is the controllability matrix of A b and pcs is the Ackermann’s Formula Here is the controllability matrix of [A, b], and pc(s) is the](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-30.jpg)
Ackermann’s Formula Here is the controllability matrix of [A, b], and pc(s) is the desired closed-loop system characteristic polynomial. Spectral Approach where Here, i and i are the open-loop system and desired closed-loop system poles, respectively, and the vi´ are the associated reciprocal eigenvectors. Control Systems Centre - UMIST

Mapping Approach The state-feedback matrix is given as where is the controllability matrix of [A, b] Here, the ai and i are the coefficients of the open-loop and closed-loop system characteristic polynomials, respectively. Control Systems Centre - UMIST

Eigenvector Methods It is also possible to determine the statefeedback pole assignment compensator as where the mi are randomly chosen scalars and the uci are the closed-loop system eigenvectors calculated from Selecting mi =1, for example, the statefeedback compensator can be found as Control Systems Centre - UMIST

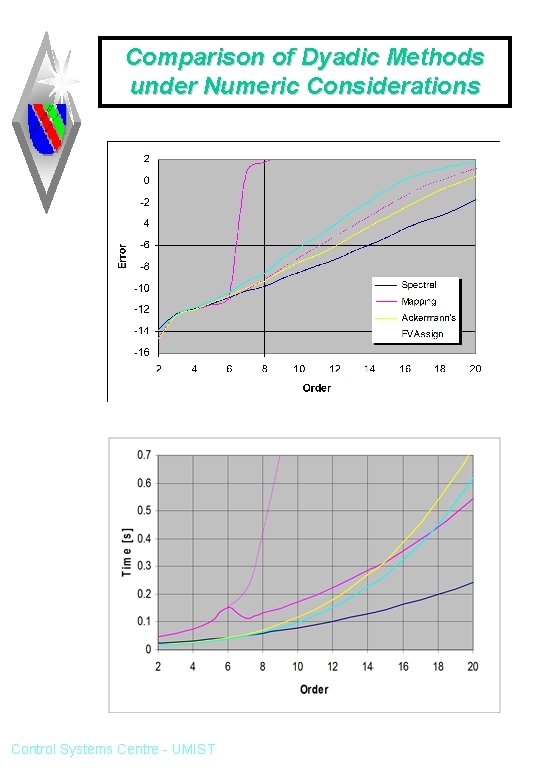
Comparison of Dyadic Methods under Numeric Considerations Control Systems Centre - UMIST

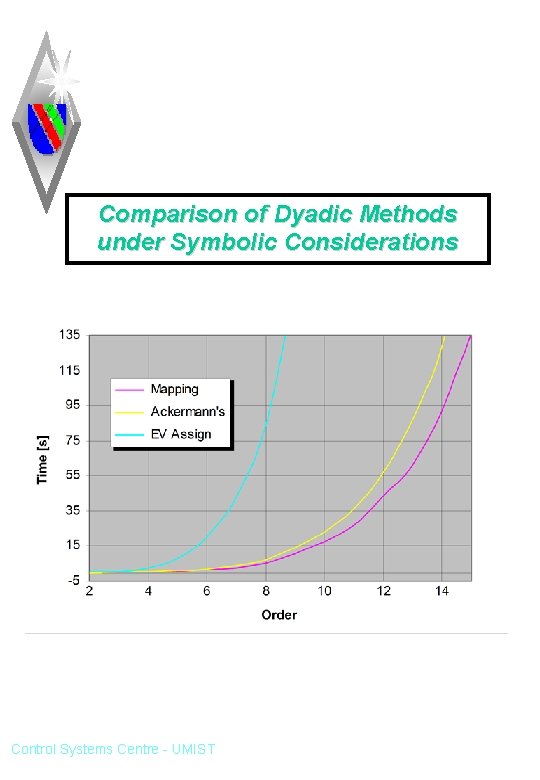
Comparison of Dyadic Methods under Symbolic Considerations Control Systems Centre - UMIST

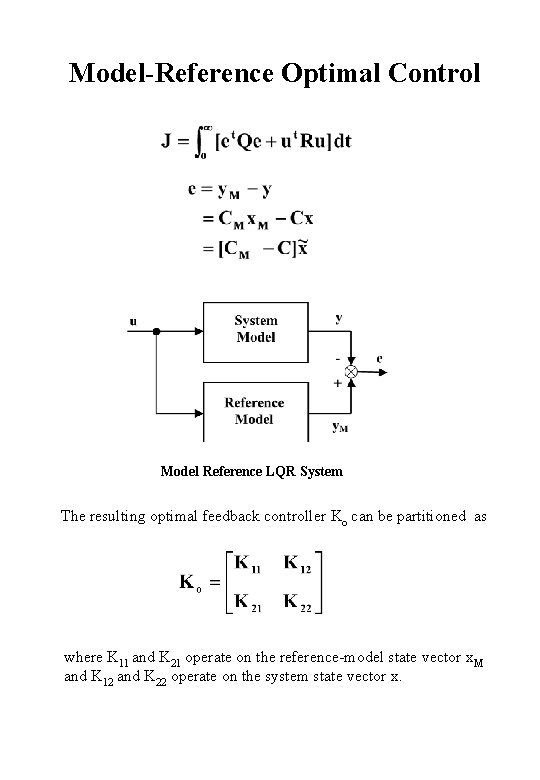
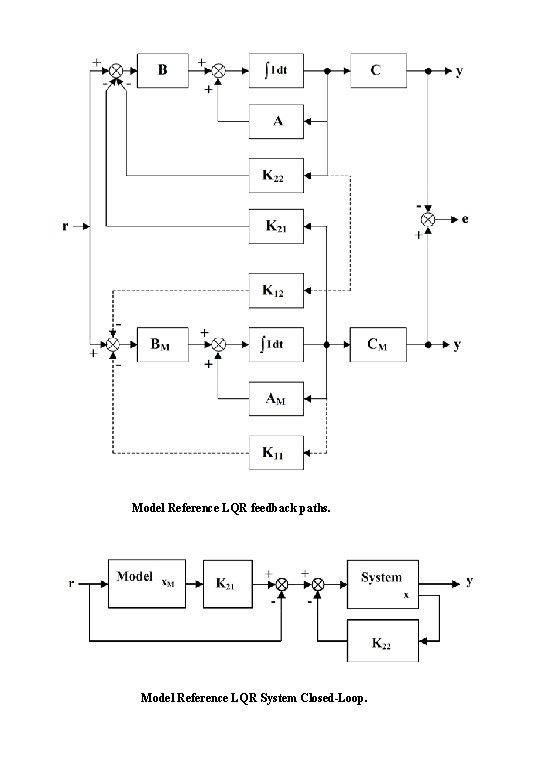
Model-Reference Optimal Control Model Reference LQR System The resulting optimal feedback controller Ko can be partitioned as where K 11 and K 21 operate on the reference-model state vector x. M and K 12 and K 22 operate on the system state vector x.

Model Reference LQR feedback paths. Model Reference LQR System Closed-Loop.


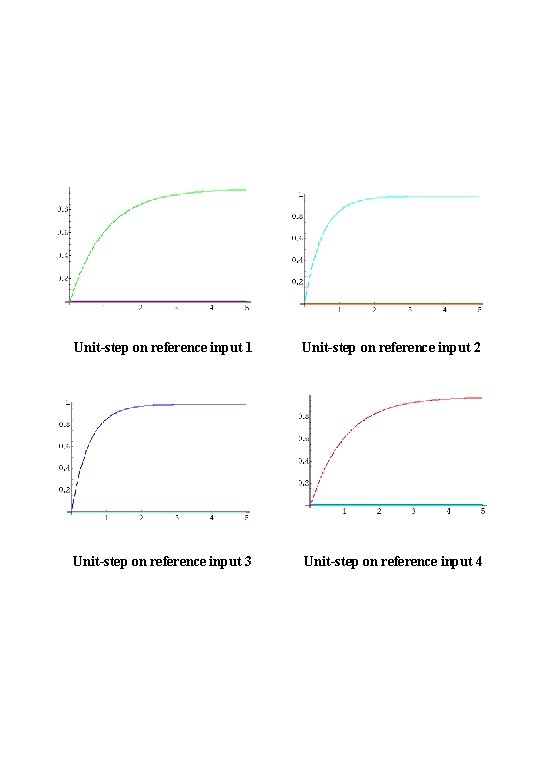
Unit-step on reference input 1 Unit-step on reference input 2 Unit-step on reference input 3 Unit-step on reference input 4

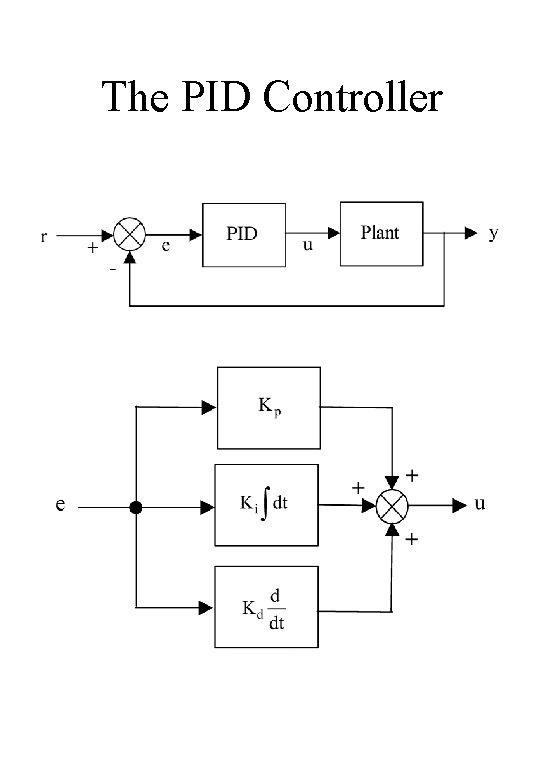
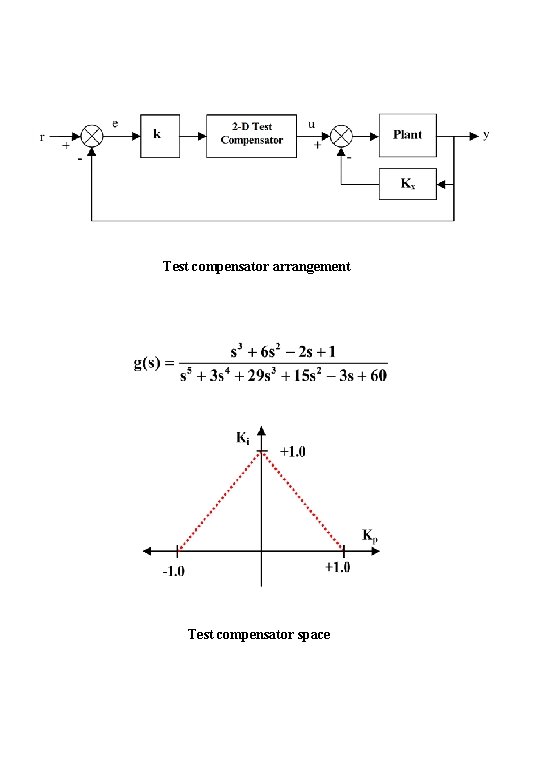
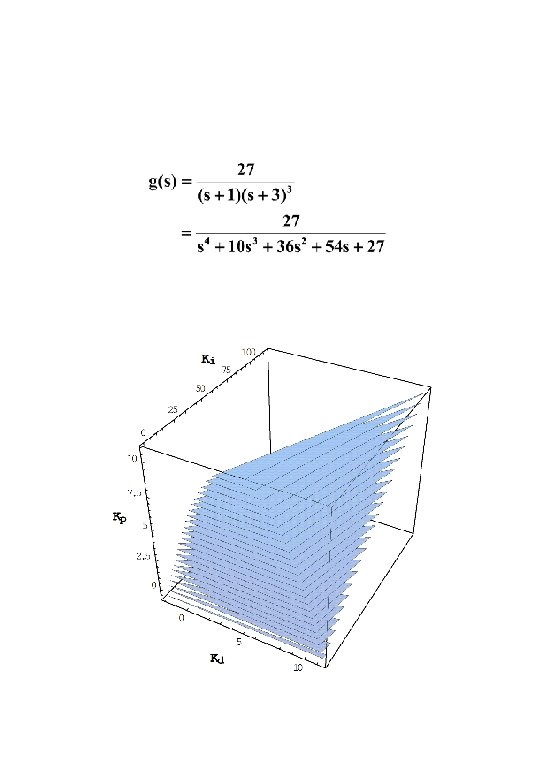
The PID Controller • In recent years, several researchers have been re -examining the PID controller to determine the limiting Kp, Ki, and Kd parameter values to guarantee a stable closed-loop system; namely, • Keel and Bhattacharyya • Ho, Datta, and Bhattacharyya • Shafei and Shenton • Astrom and Hagglund • Munro and Soylemez

The PID Controller

Test compensator arrangement Test compensator space

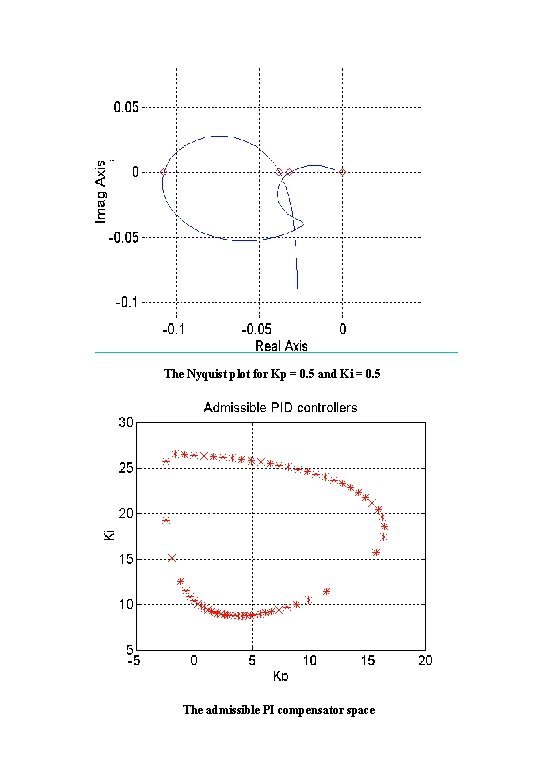
The Nyquist plot for Kp = 0. 5 and Ki = 0. 5 The admissible PI compensator space


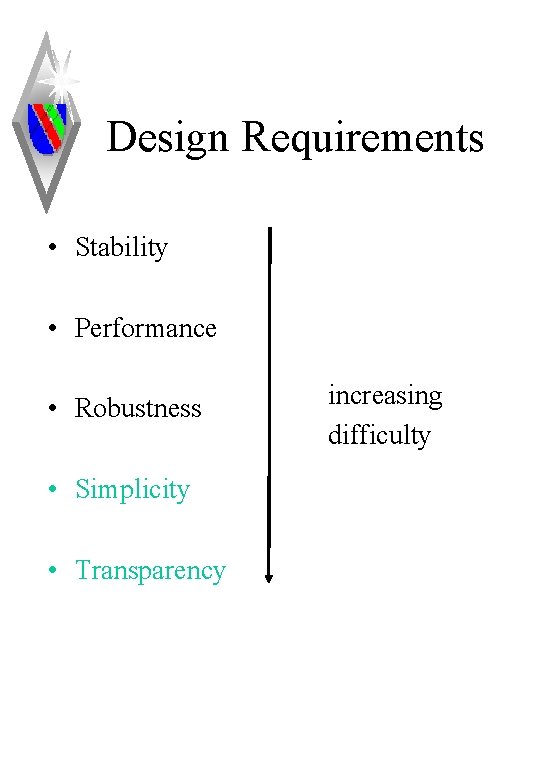
Design Requirements • Stability • Performance • Robustness • Simplicity • Transparency increasing difficulty

Acknowledgements My thanks to Dr Igor Bakshee of Wolfram Research for his interest and help in carrying out this work.

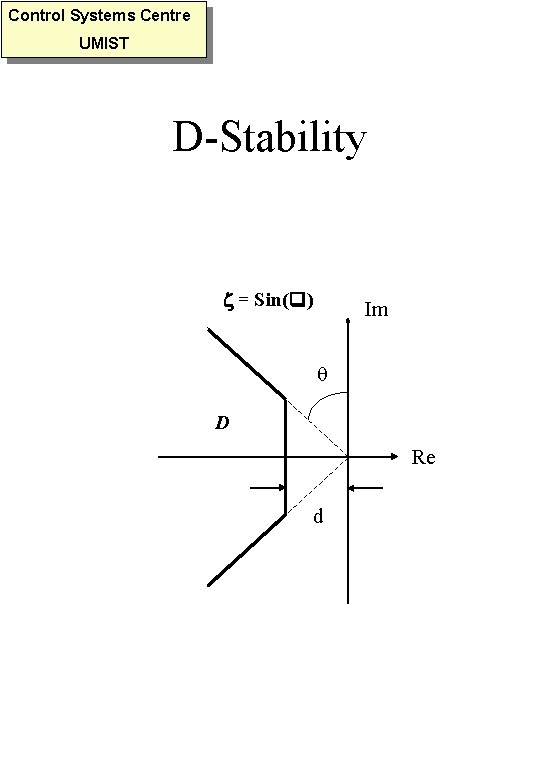
Control Systems Centre UMIST D-Stability = Sin( ) Im D Re d

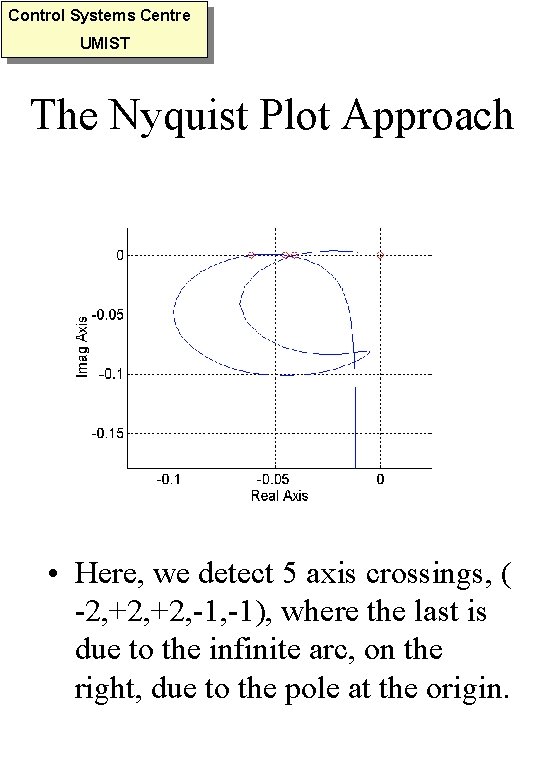
Control Systems Centre UMIST The Nyquist Plot Approach • Here, we detect 5 axis crossings, ( -2, +2, -1), where the last is due to the infinite arc, on the right, due to the pole at the origin.

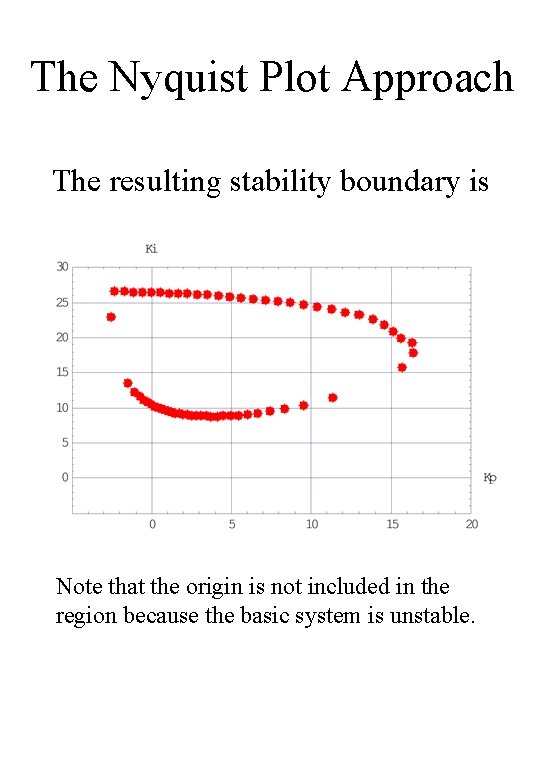
The Nyquist Plot Approach The resulting stability boundary is Note that the origin is not included in the region because the basic system is unstable.

Control Systems Centre UMIST The Nyquist Plot Approach • Here, with Kp = 5 and Ki = 18 the system is stable, even with an additional gain of k =1. 3134 • • yielding closed-loop poles = -0. 2519 ± 5. 4879 i -1. 2320 ± 1. 5258 i -0. 0161 ± 0. 4510 i

Diagonal Dominance Concepts Various definitions of Diagonal Dominance exist, namely : Rosenbrock’s row/column form ~ R Limebeer’s Generalised Diagonal Dominance ~ L Bryant & Yeung’s Fundamental Dominance ~ Y where the conservatism of the resulting dominance criterion reduces as Y<L<R Mathematica Code

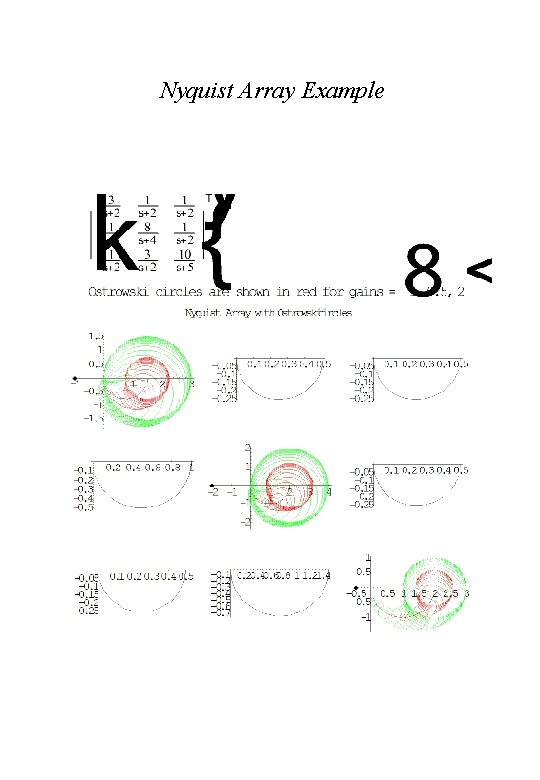
Nyquist Array Example

Gasifier Model Format A is 25 x 25 C is 4 x 25 Inputs: - 1 char 2 air 3 coal 4 steam 5 limestone 6 upstream disturbance B is 25 x 6 D is 4 x 6 Outputs: - 1 gas cv 2 bed mass 3 gas pressure 4 gas temperature

Combined Sequential Loop Closing and Diagonal Dominance Method • This approach is a new combination of Bryant’s Sequential Loop Closing Approach with Mac. Farlane and Kouvaritakis’ ALIGN Algorithm, Edmunds’ Scaling and Normalization Technique, and Rosenbrock’s Diagonal Dominance. • It is particularly appropriate in cases where a simple controller structure is desired. • Advantages: – It can be implemented by closing one loop at a time. – Usually, the resulting control scheme is quite simple and can be easily realized in practice.

Achieving Diagonal Dominance • Normalization : – Generates the input-output scaling to be applied to the system in order to minimize interaction. – Determines the best input-output pairing for control purposes. – Produces good diagonal dominance properties at low and intermediate frequencies. – Results are obtained by using simple, wholly real permutation matrices. • High frequency decoupling : – Aims at improving the transient response of the system. – Emphasis is on frequencies close to the bandwidth, around which interaction is most severe. – Results are obtained by making use of wholly real matrices.

Preliminary Analysis The original 25 th order system is numerically very ill conditioned. The eigenvalues cover a significant range in the complex plane, ranging from -0. 00033 to -33. 1252. The condition number is 5. 24 x 1019. At w = 0 the maximum and minimum singular values are 147500 and 50, respectively. The Kalman controllability and observability tests yield a rank of 1, and the controllability and observability gramians are : -
![Preliminary Analysis Application of the decoupling zeros algorithm to s IA B yielded Dimensions Preliminary Analysis Application of the decoupling zeros algorithm to [s. I-A, B] yielded Dimensions](https://slidetodoc.com/presentation_image_h/ac61a1bd2d1a86bce06e1d9122d84873/image-56.jpg)
Preliminary Analysis Application of the decoupling zeros algorithm to [s. I-A, B] yielded Dimensions of indicating that the system had 7 input-decoupling zeros, which was confirmed by transforming A and B to spectral form.





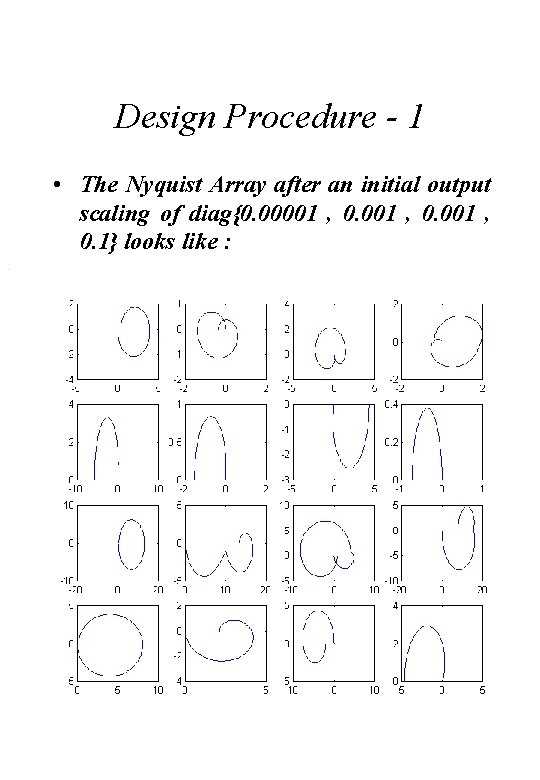
Design Procedure - 1 • The Nyquist Array after an initial output scaling of diag{0. 00001 , 0. 1} looks like :

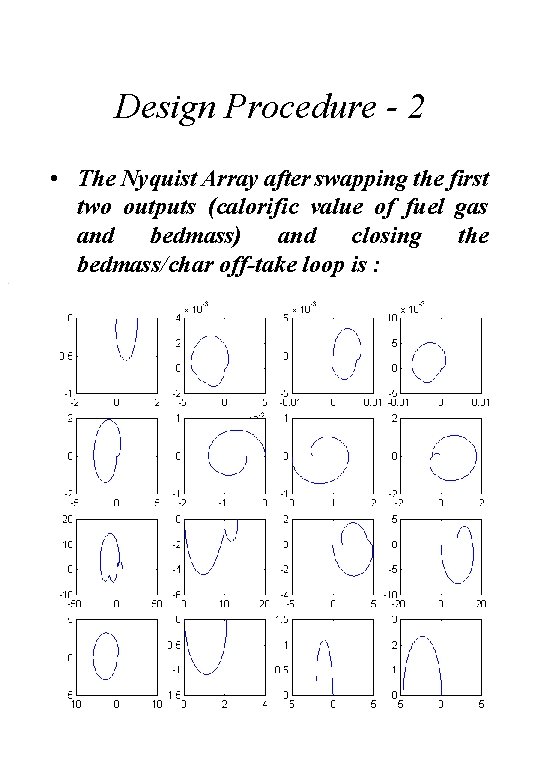
Design Procedure - 2 • The Nyquist Array after swapping the first two outputs (calorific value of fuel gas and bedmass) and closing the bedmass/char off-take loop is :

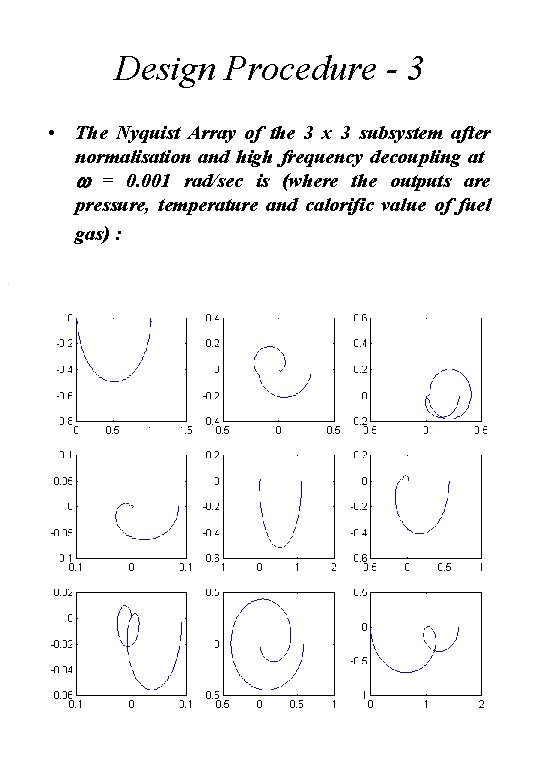
Design Procedure - 3 • The Nyquist Array of the 3 x 3 subsystem after normalisation and high frequency decoupling at w = 0. 001 rad/sec is (where the outputs are pressure, temperature and calorific value of fuel gas) :

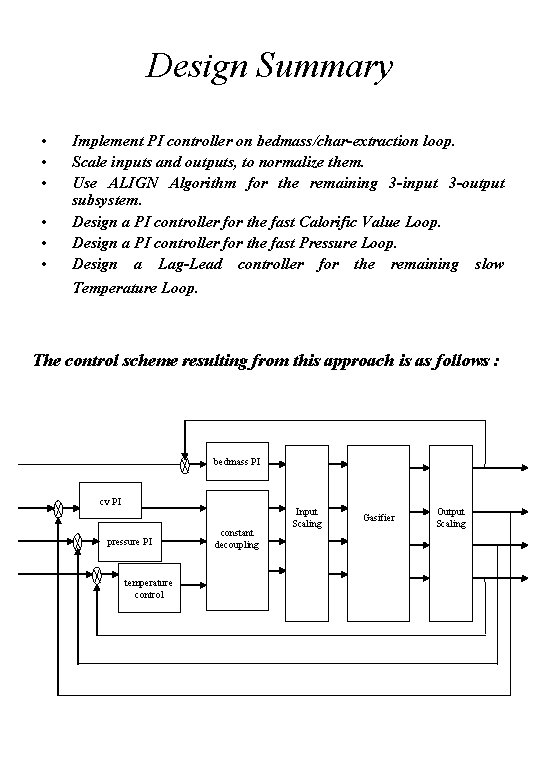
Design Summary • • • Implement PI controller on bedmass/char-extraction loop. Scale inputs and outputs, to normalize them. Use ALIGN Algorithm for the remaining 3 -input 3 -output subsystem. Design a PI controller for the fast Calorific Value Loop. Design a PI controller for the fast Pressure Loop. Design a Lag-Lead controller for the remaining slow Temperature Loop. The control scheme resulting from this approach is as follows : bedmass PI cv PI pressure PI temperature control constant decoupling Input Scaling Gasifier Output Scaling

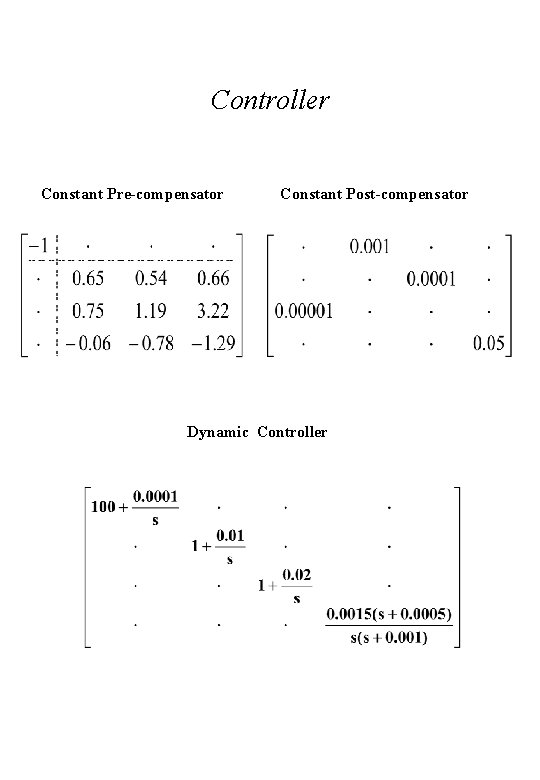
Controller Constant Pre-compensator Constant Post-compensator Dynamic Controller

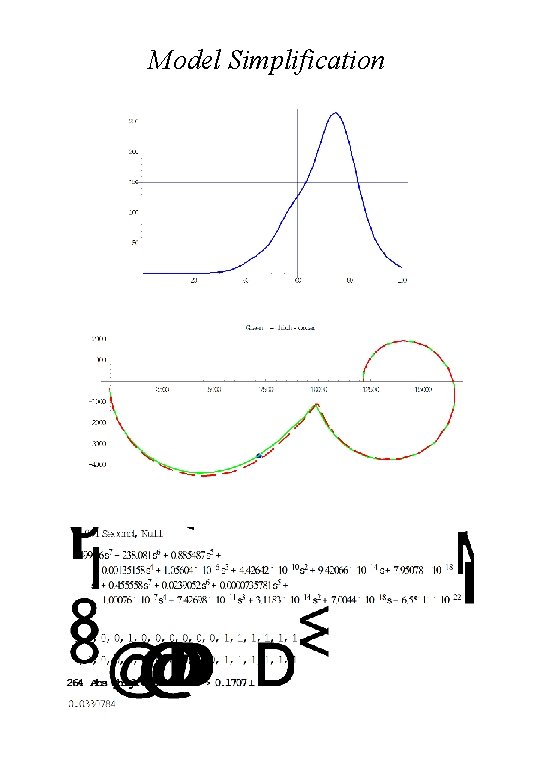
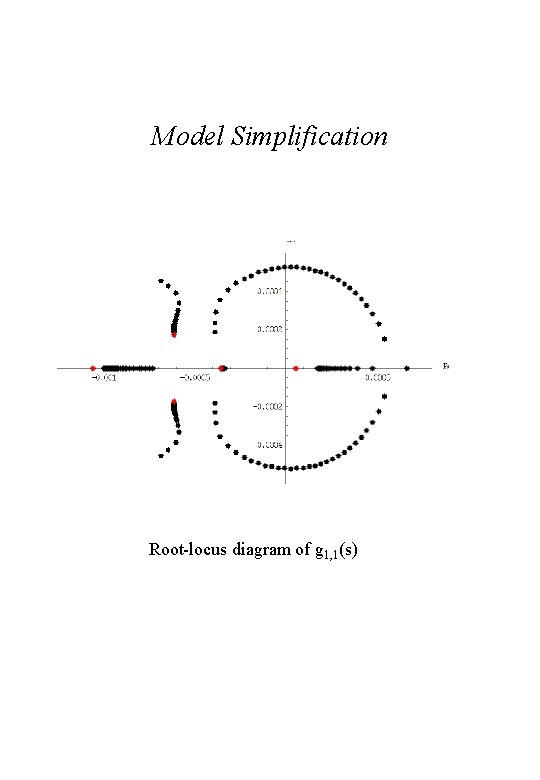
Model Simplification

Model Simplification Root-locus diagram of g 1, 1(s)

Theorem: By using just the first input of a given MIMO system, it is almost always possible to arbitrarily assign 1 self conjugate poles of the system, and make these poles uncontrollable from the other inputs, provided that the system [A, b 1, C] has 1 controllable and observable poles, where b 1 is the first column of the input matrix (B), where This result can be compared with a previous result developed by Munro and Novin-Hirbod (1979) for the case of dynamic output feedback, where the degree r of the necessary compensator is given by
 Sneg mathematica
Sneg mathematica Mathematica unicamp
Mathematica unicamp Calculus of residues
Calculus of residues Mathematica export animation
Mathematica export animation Mathematica exercises
Mathematica exercises Input director 사용법
Input director 사용법 Legendre polynomial
Legendre polynomial Schrodinger equation radial solution
Schrodinger equation radial solution Mathematica
Mathematica Mathematica
Mathematica Mathematica
Mathematica Mathematica text
Mathematica text Framebuffer compression
Framebuffer compression Central force
Central force Willy aims
Willy aims Accelerate day 2
Accelerate day 2 Nabla operator
Nabla operator Absolute timing mathematica
Absolute timing mathematica Nrg code
Nrg code Hakan kutucu
Hakan kutucu Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Frameset trong html5
Frameset trong html5 Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Gấu đi như thế nào
Gấu đi như thế nào Chụp tư thế worms-breton
Chụp tư thế worms-breton Bài hát chúa yêu trần thế alleluia
Bài hát chúa yêu trần thế alleluia Các môn thể thao bắt đầu bằng tiếng nhảy
Các môn thể thao bắt đầu bằng tiếng nhảy Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính độ biến thiên đông lượng
Công thức tính độ biến thiên đông lượng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân Phép trừ bù
Phép trừ bù độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng nó xinh thế chỉ nói điều hay thôi
Cái miệng nó xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ V cc cc
V cc cc Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Phối cảnh
Phối cảnh Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là Dot
Dot Số.nguyên tố
Số.nguyên tố Tư thế ngồi viết
Tư thế ngồi viết Lời thề hippocrates
Lời thề hippocrates Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan ưu thế lai là gì
ưu thế lai là gì Sự nuôi và dạy con của hổ
Sự nuôi và dạy con của hổ Khi nào hổ con có thể sống độc lập
Khi nào hổ con có thể sống độc lập Sơ đồ cơ thể người
Sơ đồ cơ thể người Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi What is system design in software engineering
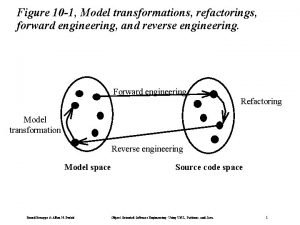
What is system design in software engineering Forward engineering in software engineering
Forward engineering in software engineering Dicapine
Dicapine Elegant systems
Elegant systems Forward and reverse engineering
Forward and reverse engineering Dr neil munro
Dr neil munro Neil tang
Neil tang