The Friendship Theorem Dr John S Caughman Portland

The Friendship Theorem Dr. John S. Caughman Portland State University

Public Service Announcement “Freshman’s Dream” (a+b)p=ap+bp …mod p …when a, b are integers …and p is prime.

Freshman’s Dream Generalizes! (a 1+a 2+…+an)p=a 1 p +a 2 p +…+anp …mod p …when a, b are integers …and p is prime.

Freshman’s Dream Generalizes A= a 1 0 0 0 * a 2 0 0 * * a 3 0 * * * a 4 (a 1+a 2+…+an)p = a 1 p +a 2 p +…+anp tr(A) p = tr(Ap) (mod p)

Freshman’s Dream Generalizes! A= * * * * tr(A) p = tr(Ap) (mod p) tr(A p) = tr((L+U)p) = tr(Lp +Up) = tr(Lp)+tr(Up)=0+tr(U)p = tr(A)p Note: tr(UL)=tr(LU) so cross terms combine , and coefficients =0 mod p.

The Theorem If every pair of people at a party has precisely one common friend, then there must be a person who is everybody's friend.

Cheap Example Nancy John Mark

Cheap Example of a Graph Nancy John Mark

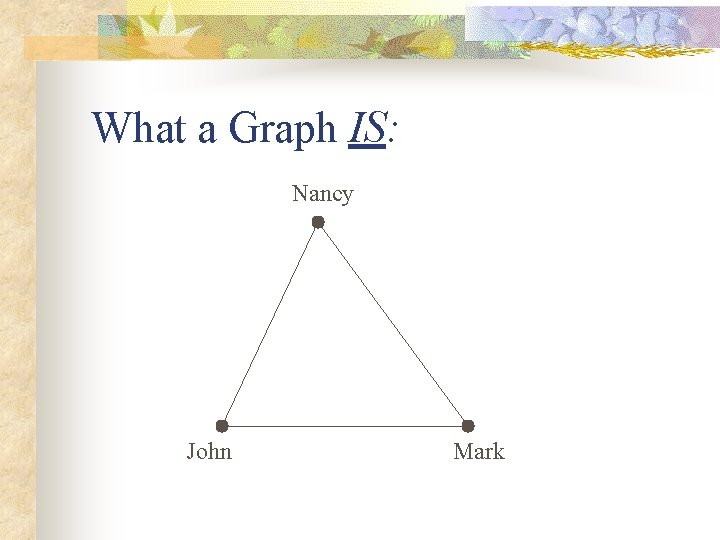
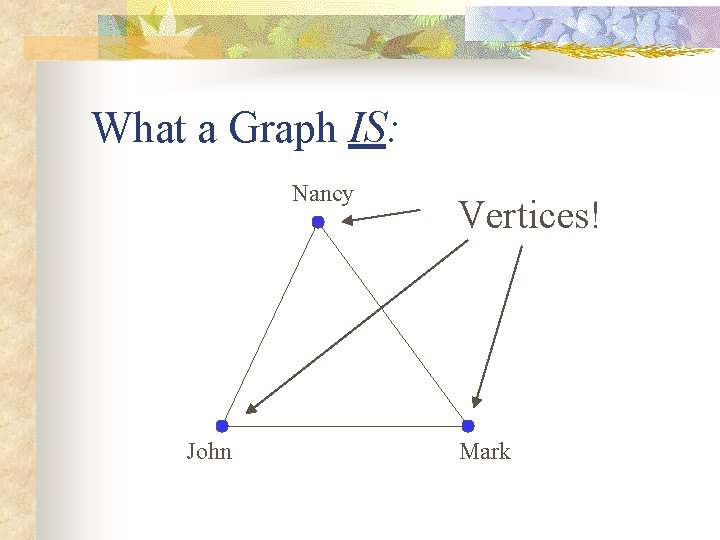
What a Graph IS: Nancy John Mark

What a Graph IS: Nancy John Vertices! Mark

What a Graph IS: Nancy John Edges! Mark

What a Graph IS NOT: Nancy John Mark

What a Graph IS NOT: Nancy John Loops! Mark

What a Graph IS NOT: Nancy John Loops! Mark

What a Graph IS NOT: Nancy John Directed edges! Mark

What a Graph IS NOT: Nancy John Directed edges! Mark

What a Graph IS NOT: Nancy John Multi-edges! Mark

What a Graph IS NOT: Nancy John Multi-edges! Mark

‘Simple’ Graphs… Nancy John • Finite • Undirected • No Loops • No Multiple Edges Mark

The Theorem, Restated Let G be a simple graph with n vertices. If every pair of vertices in G has precisely one common neighbor, then G has a vertex with n-1 neighbors.

The Theorem, Restated Generally attributed to Erdős (1966). Easily proved using linear algebra. Combinatorial proofs more elusive.

NOT A TYPICAL “THRESHOLD” RESULT

Pigeonhole Principle If more than n pigeons are placed into n or fewer holes, then at least one hole will contain more than one pigeon.

Some threshold results If a graph with n vertices has > n 2/4 edges, then there must be a set of 3 mutual neighbors. If it has > n(n-2)/2 edges, then there must be a vertex with n-1 neighbors.

Extremal Graph Theory If this were an extremal problem, we would expect graphs with MORE edges than ours to also satisfy the same conclusion…

1

1 2

1 2 3

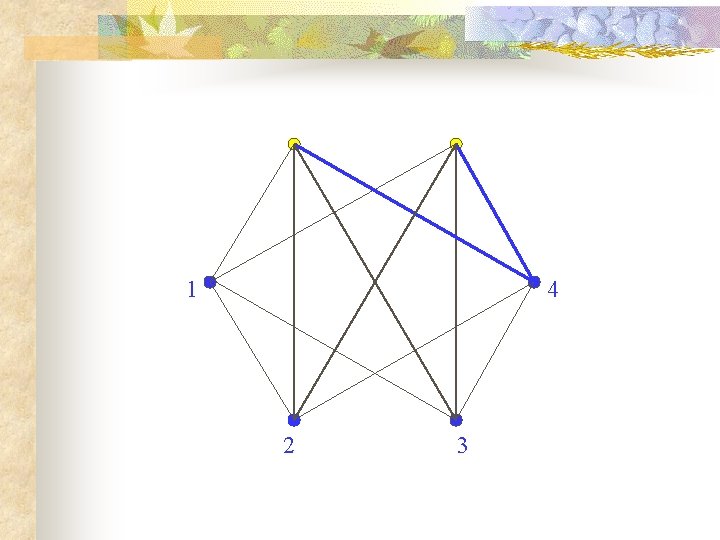
1 4 2 3

4

4

4

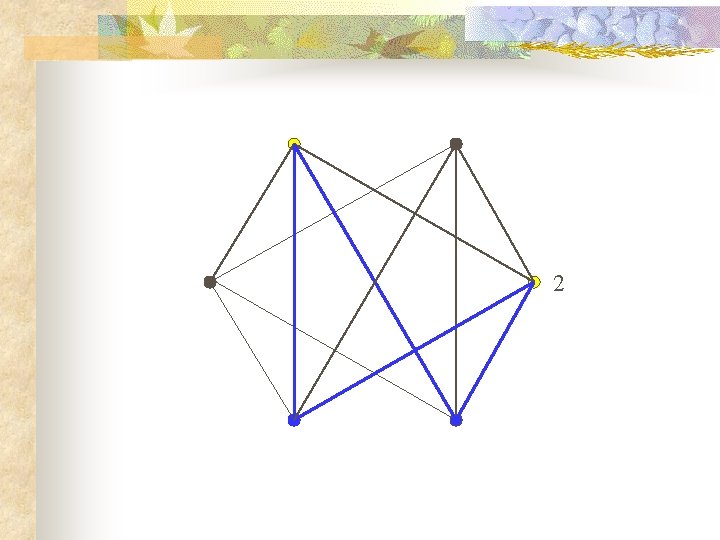
2

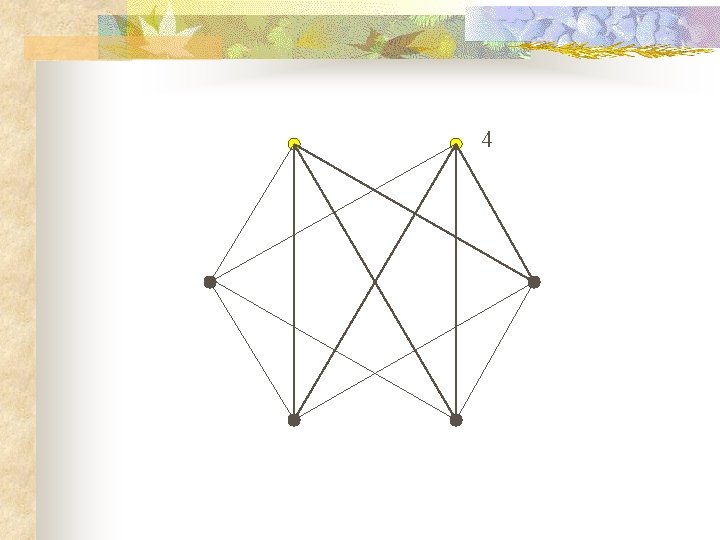
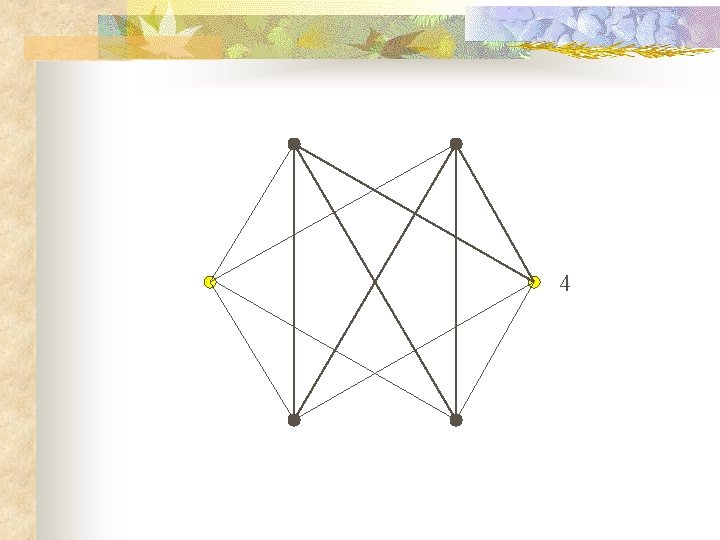
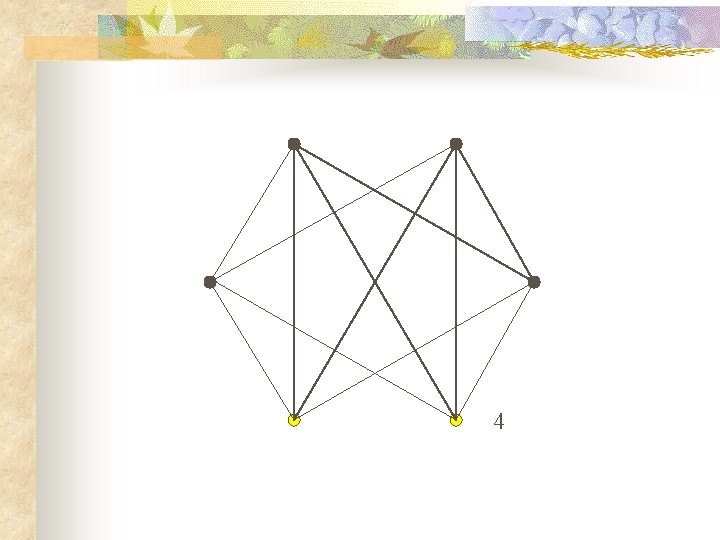
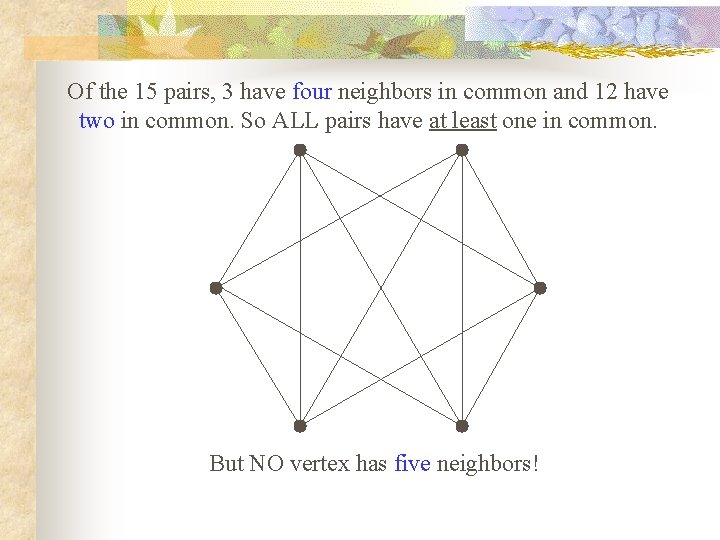
Of the 15 pairs, 3 have four neighbors in common and 12 have two in common. So ALL pairs have at least one in common. But NO vertex has five neighbors!

Related Fact – losing edges

Related Fact – losing edges

Related Fact – losing edges

Summary If every pair of vertices in a graph has at least one neighbor in common, it might not be possible to remove edges and produce a subgraph in which every pair has exactly one common neighbor.

Accolades for Friendship n The Friendship Theorem is listed among Abad's “ 100 Greatest Theorems” n The proof is immortalized in Aigner and Ziegler's Proofs from THE BOOK.

Example 1

Example 2

Example 3

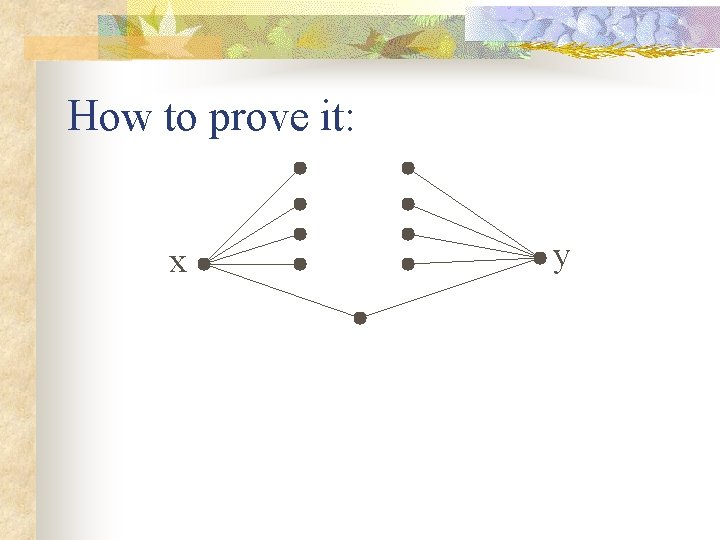
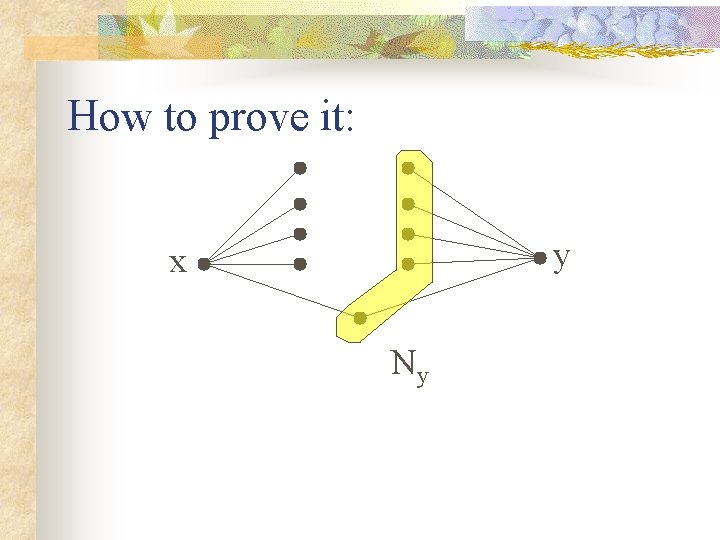
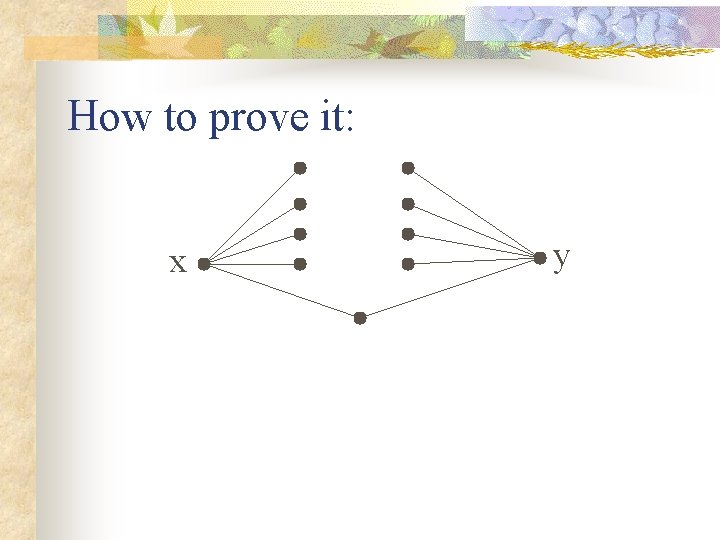
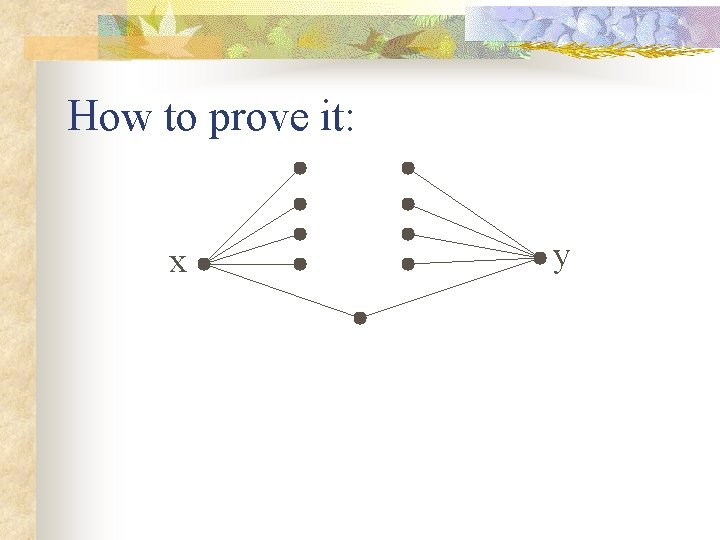
How to prove it: STEP ONE: If x and y are not neighbors, they have the same # of neighbors. Why: Let Nx = set of neighbors of x Let Ny = set of neighbors of y

How to prove it: x y

How to prove it: y x Nx

How to prove it: y x Ny

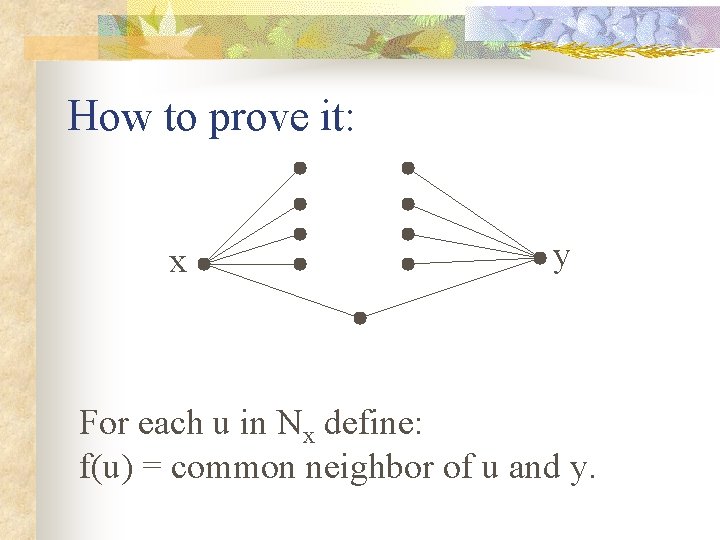
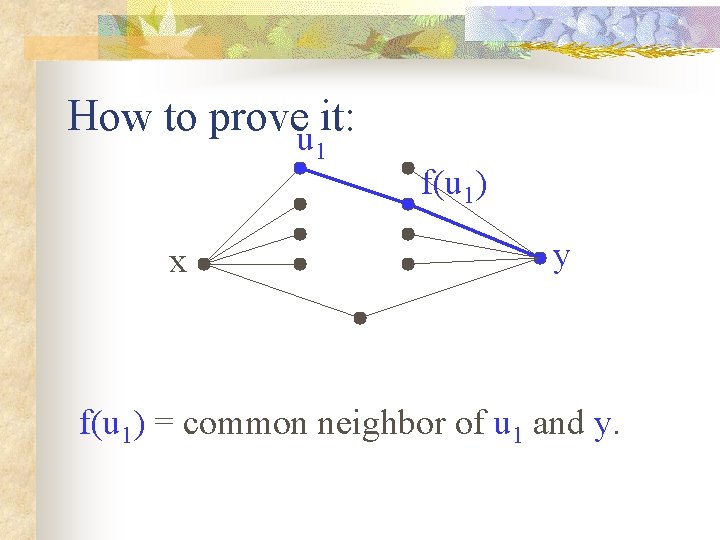
How to prove it: x y For each u in Nx define: f(u) = common neighbor of u and y.

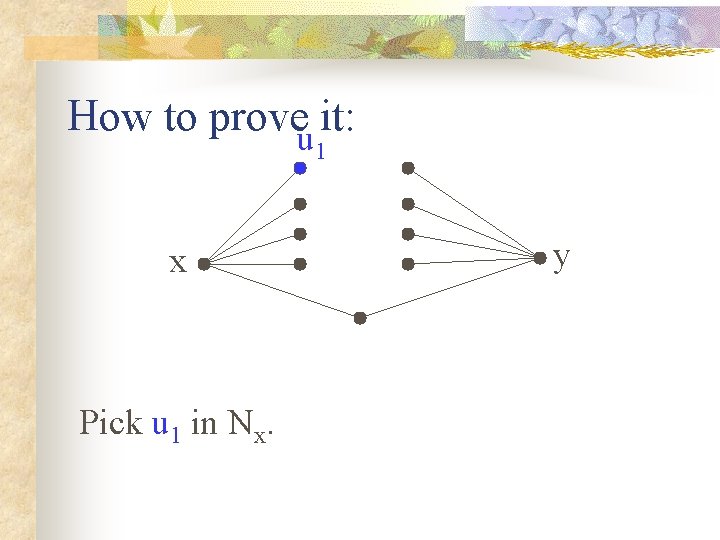
How to proveu it: 1 x Pick u 1 in Nx. y

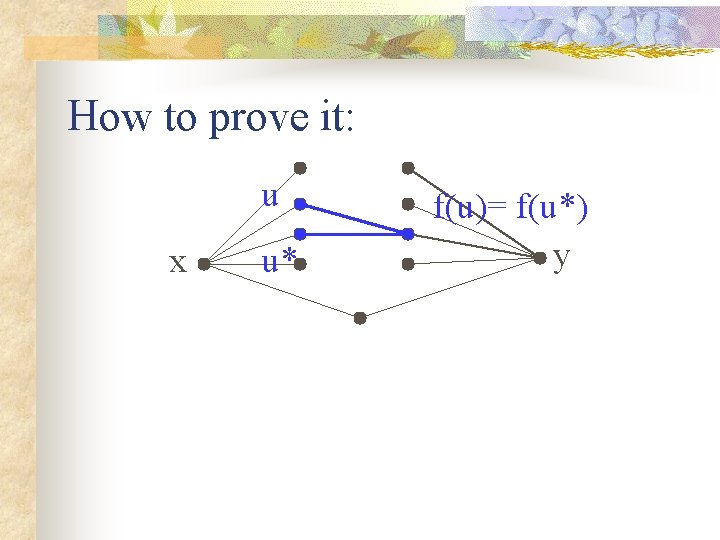
How to proveu it: 1 x f(u 1) y f(u 1) = common neighbor of u 1 and y.

How to prove it: x y

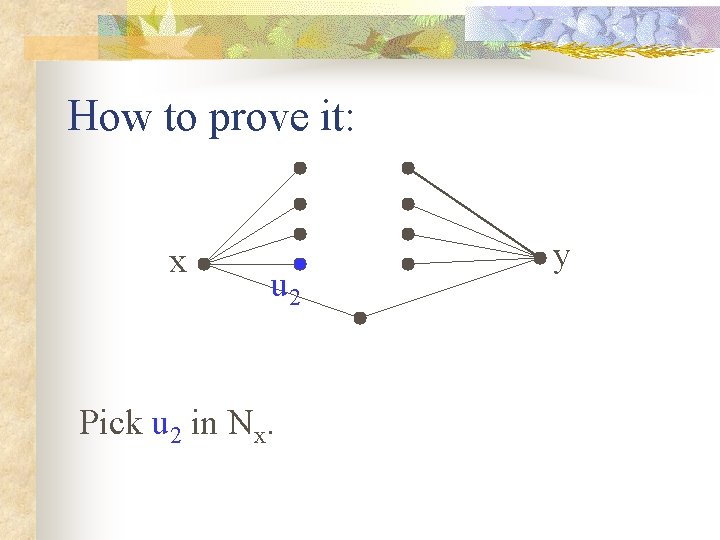
How to prove it: x u 2 Pick u 2 in Nx. y

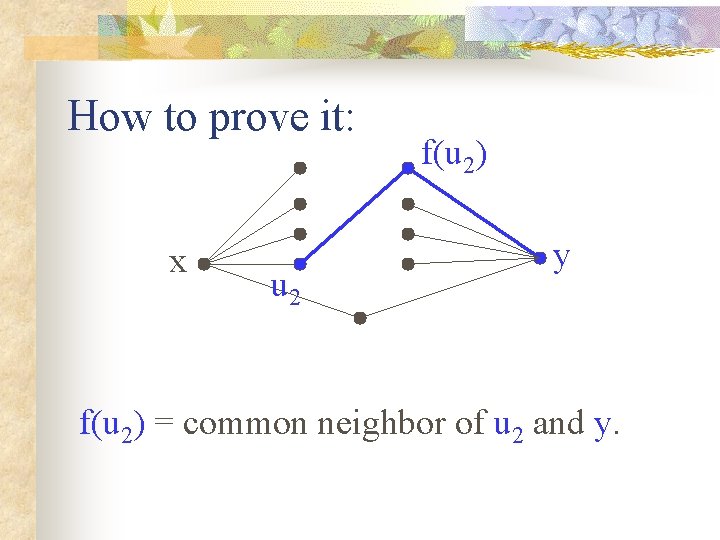
How to prove it: x u 2 f(u 2) y f(u 2) = common neighbor of u 2 and y.

How to prove it: x y

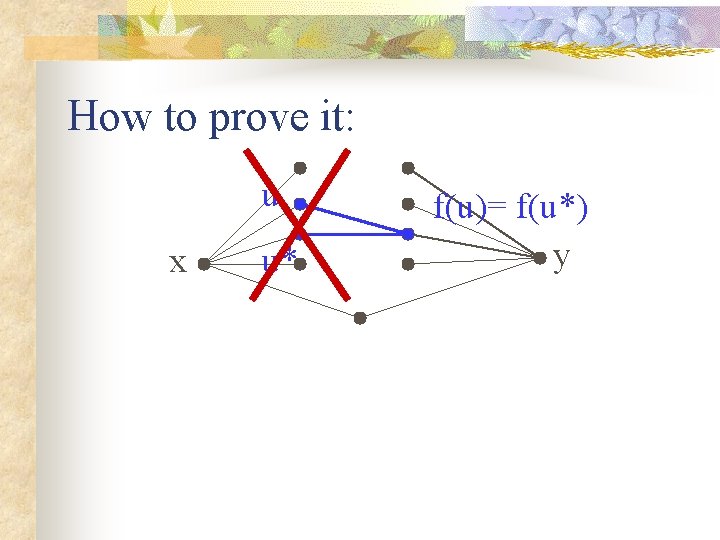
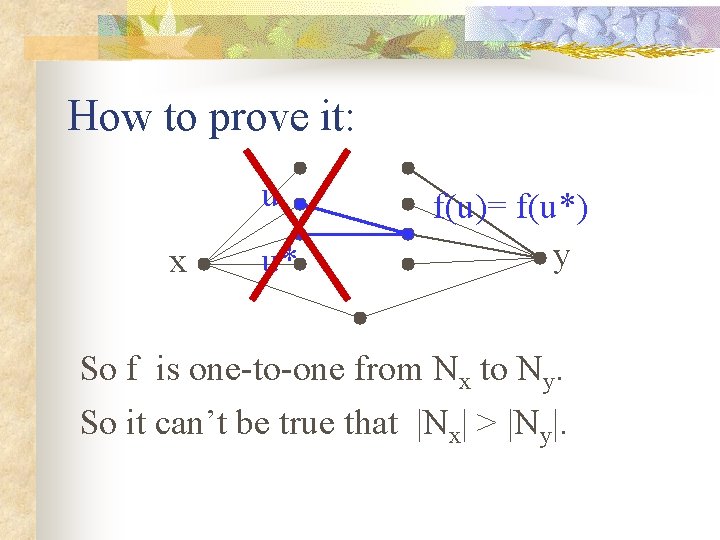
How to prove it: u x u* f(u)= f(u*) y

How to prove it: u x u* f(u)= f(u*) y

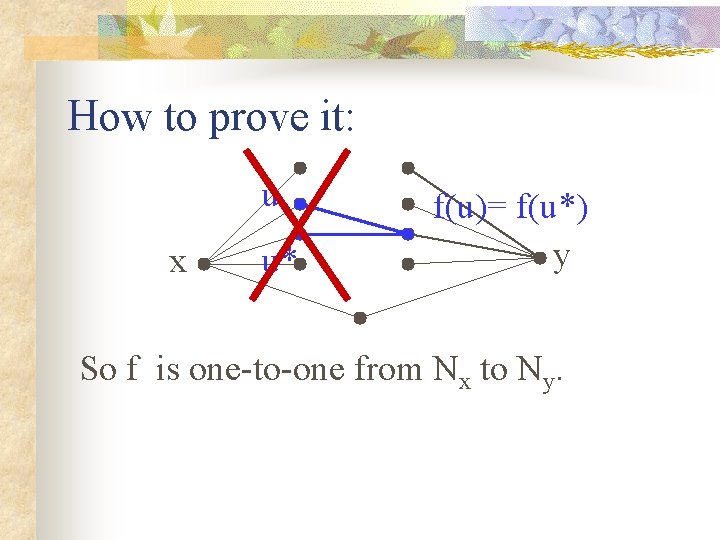
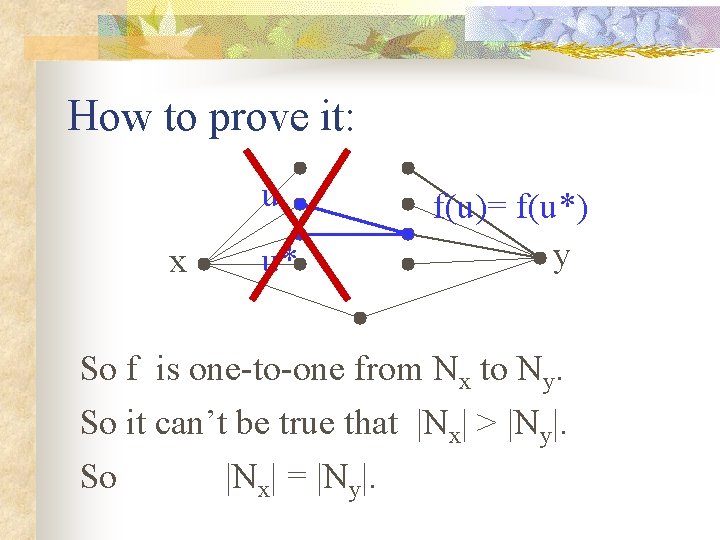
How to prove it: u x u* f(u)= f(u*) y So f is one-to-one from Nx to Ny.

How to prove it: u x u* f(u)= f(u*) y So f is one-to-one from Nx to Ny. So it can’t be true that |Nx| > |Ny|.

How to prove it: u x u* f(u)= f(u*) y So f is one-to-one from Nx to Ny. So it can’t be true that |Nx| > |Ny|. So |Nx| = |Ny|.

How to prove it: STEP 1: If x and y are not neighbors, they have the same # of neighbors. STEP 2: Either some x has n-1 neighbors or ALL vertices have same # of neighbors. Why: Assume no vertex has n-1 neighbors. Let A = {x : x has max # of neighbors, k}. B = {y : y has < k neighbors}.

A = {x : x has max # of neighbors, k}. B = {y : y has < k neighbors}. By Step 1, all in A are neighbors to all in B! Set || Possible Size A 0, 1, 2, …. , n B 0, 1, 2, …. , n .

How to prove it: STEP 1: If x and y are not neighbors, they have the same # of neighbors. STEP 2: Either some x has n-1 neighbors or ALL vertices have k neighbors. STEP 3: If all vertices have k neighbors, then n = k (k-1) + 1.

How to prove it: STEP 3: If all vertices have k neighbors, then n = k (k-1) + 1. Why: Count paths of length 2…

How to prove it: STEP 3: If all vertices have k neighbors, then n = k (k-1) + 1. Why: Count paths of length 2… (2 ) n

How to prove it: STEP 3: If all vertices have k neighbors, then n = k (k-1) + 1. Why: Count paths of length 2… (2 ) n 1

How to prove it: STEP 3: If all vertices have k neighbors, then n = k (k-1) + 1. Why: Count paths of length 2… (2 ) n 1 =

How to prove it: STEP 3: If all vertices have k neighbors, then n = k (k-1) + 1. Why: Count paths of length 2… (2 ) n 1 = n

How to prove it: STEP 3: If all vertices have k neighbors, then n = k (k-1) + 1. Why: Count paths of length 2… (2 ) n 1 = n (k)

How to prove it: STEP 3: If all vertices have k neighbors, then n = k (k-1) + 1. Why: Count paths of length 2… (2 ) n 1 = n (k) (k-1)

How to prove it: STEP 3: If all vertices have k neighbors, then n = k (k-1) + 1. Why: Count paths of length 2… (2 ) n n (k) (k-1) 1 = ____ 2

How to prove it: STEP 3: If all vertices have k neighbors, then n = k (k-1) + 1. ( ) n n (k) (k-1) 1 = ____ 2 2 n (k) (k-1) (n)(n-1) = ____ 2 2 n = k (k-1) + 1

How to prove it: STEP 1: If x and y are not neighbors, they have the same # of neighbors. STEP 2: Either some x has n-1 neighbors or ALL vertices have k neighbors. STEP 3: If all vertices have k neighbors, then n = k (k-1) + 1.

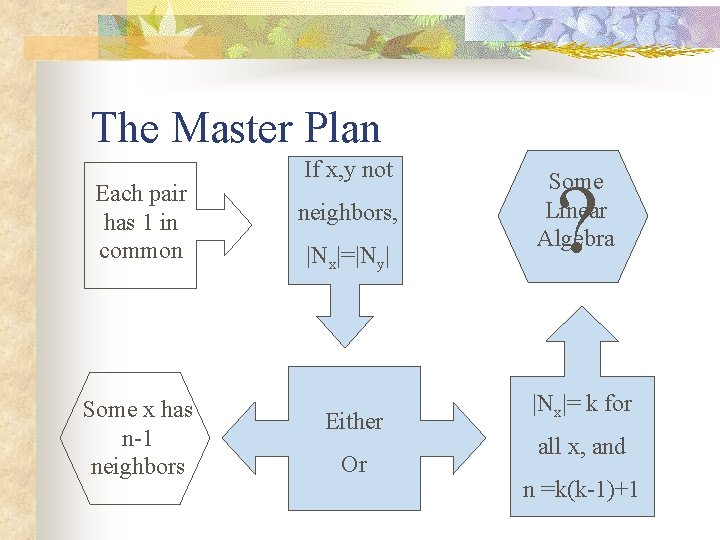
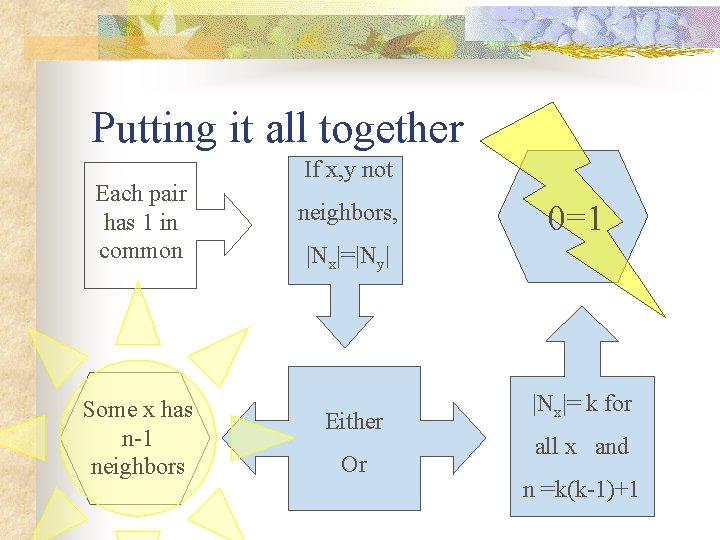
The Master Plan Each pair has 1 in common Some x has n-1 neighbors If x, y not neighbors, |Nx|=|Ny| Either Or ? Some Linear Algebra |Nx|= k for all x, and n =k(k-1)+1

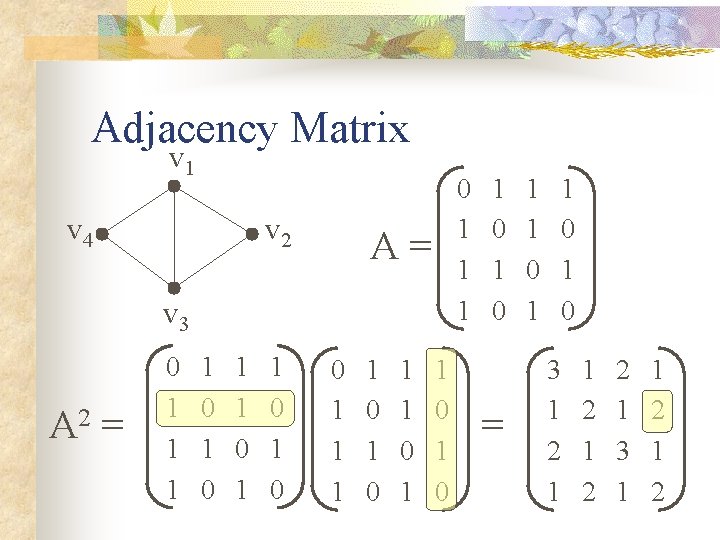
Adjacency Matrix Call vertices v 1, v 2, …, vn. Let A = n x n matrix where: Aij = 1, if vi, vj are neighbors, Aij = 0, if not. A is called the adjacency matrix of G. { Notice that the trace of A is 0.

Adjacency Matrix v 1 v 4 v 2 0 1 1 1 A= v 3 A 2 = 0 1 1 1 1 0 1 0 1 1 0 1 0 1 0 = 1 1 0 1 0 3 1 2 1 2 2 1 3 1 1 2

Adjacency Matrix (A 2) ij = # common neighbors of vi, vj So……. . for our graphs…. . (A 2) ij = 1 (A 2) ij = k if i, j different, and if i = j. A 2 = (k-1) I + J. (J = all 1’s matrix)

Adjacency Matrix A 2 = (k-1) I + J (J = all 1’s matrix) A J = (k) J Now let p be a prime divisor of k-1. Then k = 1 and n = k(k-1)+1 = 1 (mod p) So A 2 = J, and A J = J. (mod p) Therefore, Ai = J for all i > 1. (mod p)

Adjacency Matrix Ai = J But for all i > 1 (mod p) tr Ap = (tr A)p (mod p) So, modulo p, we get: 1 = n = tr J = tr Ap = (tr A)p = 0.

Putting it all together Each pair has 1 in common Some x has n-1 neighbors If x, y not neighbors, 0=1 |Nx|=|Ny| Either Or |Nx|= k for all x and n =k(k-1)+1

Moral: To make progress in almost any field of math, find a way to sneak linear algebra into it !

THANK YOU !