CRMISM Colloquium Universit Laval The New World of

CRM-ISM Colloquium Université Laval The New World of Infinite Random Geometric Graphs Anthony Bonato Ryerson University

Complex networks in the era of Big Data • web graph, social networks, biological networks, internet networks, … Infinite random geometric graphs Anthony Bonato

Hidden geometry vs Infinite random geometric graphs Anthony Bonato

Blau space • OSNs live in social space or Blau space: – each user identified with a point in a multi-dimensional space – coordinates correspond to sociodemographic variables/attributes • homophily principle: the flow of information between users is a declining function of distance in Blau space Infinite random geometric graphs Anthony Bonato

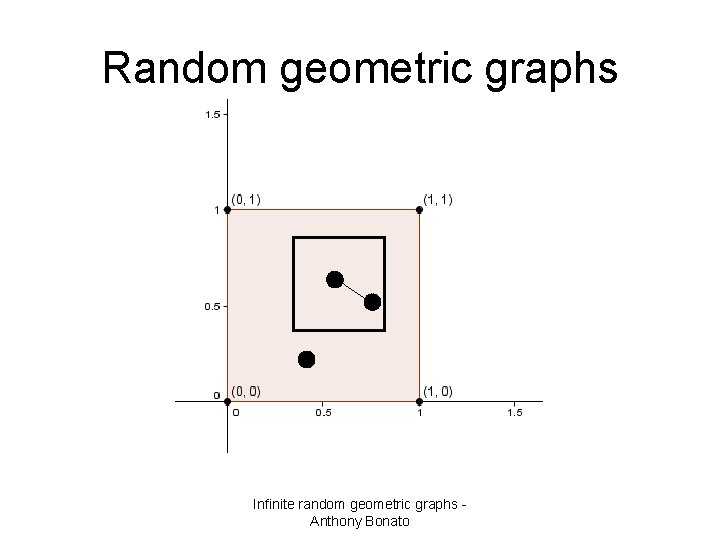
Random geometric graphs • n nodes are randomly placed in the unit square • each node has a constant sphere of influence, radius r • nodes are joined if their Euclidean distance is at most r Infinite random geometric graphs Anthony Bonato

Spatially Preferred Attachment (SPA) model (Aiello, Bonato, Cooper, Janssen, Prałat, 08) • volume of sphere of influence proportional to indegree • nodes are added and spheres of influence shrink over time • a. a. s. leads to power laws graphs, low directed diameter, and small separators Infinite random geometric graphs Anthony Bonato

Into the infinite

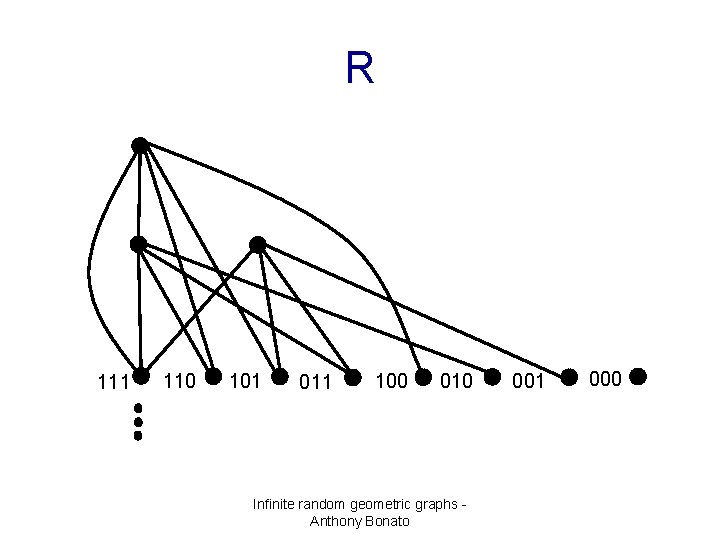
R 111 110 101 011 100 010 Infinite random geometric graphs Anthony Bonato 001 000

Properties of R • limit graph is countably infinite • every finite graph gets added eventually – infinitely often – holds also for countable graphs • add an exponential number of vertices at each time-step Infinite random geometric graphs Anthony Bonato

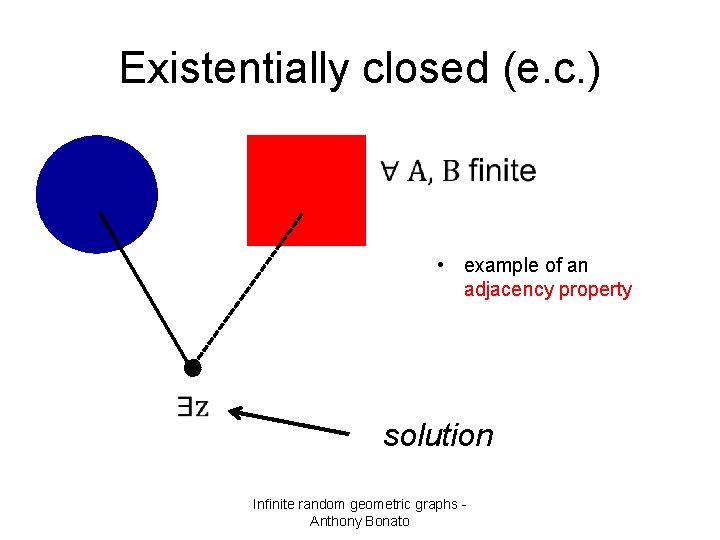
Existentially closed (e. c. ) • example of an adjacency property solution Infinite random geometric graphs Anthony Bonato

Categoricity • e. c. captures R in a strong sense Theorem (Fraïssé, 53) Any two countable e. c. graphs are isomorphic. Proof: back-and-forth argument. Infinite random geometric graphs Anthony Bonato

Explicit construction • Infinite random geometric graphs Anthony Bonato

Infinite random graphs • G(N, 1/2): – V=N – E: sample independently with probability ½ Theorem (Erdős, Rényi, 63) With probability 1, two graphs sampled from G(N, 1/2) are e. c. , and so isomorphic to R. Infinite random geometric graphs Anthony Bonato

Proof sketch • Infinite random geometric graphs Anthony Bonato

Properties of R • diameter 2 • universal • indestructible • indivisible • pigeonhole property • axiomatizes almost sure theory of graphs … Infinite random geometric graphs Anthony Bonato

More on R • A. Bonato, A Course on the Web Graph, AMS, 2008. • P. J. Cameron, The random graph, In: Algorithms and Combinatorics 14 (R. L. Graham and J. Nešetřil, eds. ), Springer Verlag, New York (1997) 333 -351. • P. J. Cameron, The random graph revisited, In: European Congress of Mathematics Vol. I (C. Casacuberta, R. M. Miró-Roig, J. Verdera and S. Xambó-Descamps, eds. ), Birkhauser, Basel (2001) 267 -274. Infinite random geometric graphs Anthony Bonato

And now for something completely different

Graphs in normed spaces • Infinite random geometric graphs Anthony Bonato

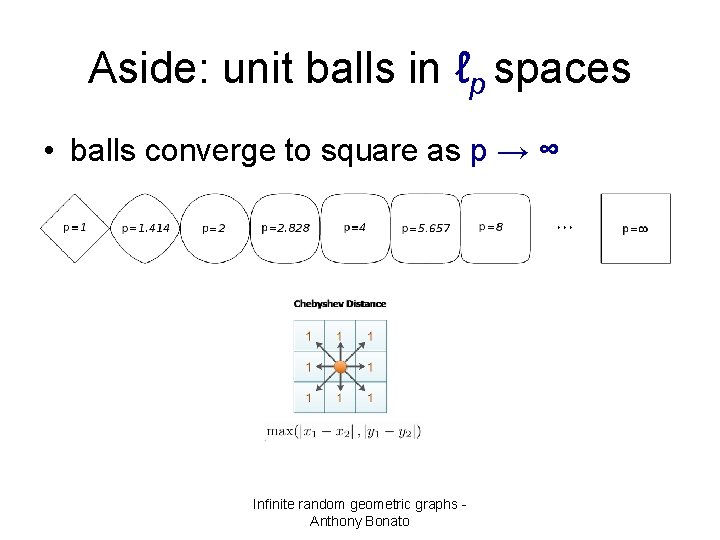
Aside: unit balls in ℓp spaces • balls converge to square as p → ∞ Infinite random geometric graphs Anthony Bonato

Random geometric graphs Infinite random geometric graphs Anthony Bonato

Local Area Random Graph (LARG) model • parameters: – p in (0, 1) – a normed space S • V: a countable set in S • E: if || u – v || < 1, then uv is an edge with probability p Infinite random geometric graphs Anthony Bonato

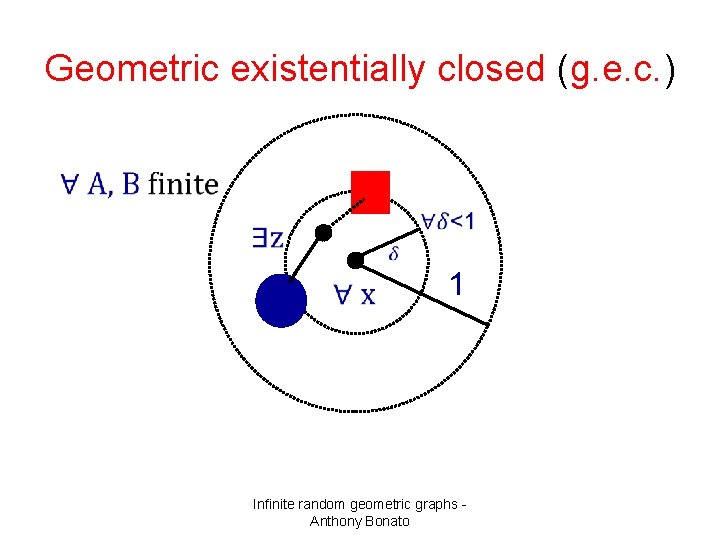
Geometric existentially closed (g. e. c. ) 1 Infinite random geometric graphs Anthony Bonato

Properties following from g. e. c • locally R • vertex sets are dense Infinite random geometric graphs Anthony Bonato

LARG graphs almost surely g. e. c. • 1 -geometric graph: g. e. c. and 1 -threshold: adjacency only may occur if distance < 1 Theorem (BJ, 11) With probability 1, and for any fixed p, LARG generates 1 geometric graphs. • proof analogous to Erdős-Rényi result for R • 1 -geometric graphs “look like” R in their unit balls, but can have diameter > 2 Infinite random geometric graphs Anthony Bonato

Geometrization lemma • Infinite random geometric graphs Anthony Bonato

Step-isometries • Infinite random geometric graphs Anthony Bonato

Example: ℓ∞ • V: dense countable set in R • E: LARG model • integer distance free (IDF) set – pairwise ℓ∞ distance non-integer • dense sets contain idf dense sets • “random” countable dense sets are idf Infinite random geometric graphs Anthony Bonato

Categoricity • countable V is Rado if the LARG graphs on it are isomorphic with probability 1 Theorem (BJ, 11) Dense idf sets in ℓ∞d are Rado for all d > 0. • new class of infinite graphs GRd which are unique limit objects of random graph processes in normed spaces Infinite random geometric graphs Anthony Bonato

Sketch of proof for d = 1 • Infinite random geometric graphs Anthony Bonato

The new world

Properties of GRd • symmetry: – step-isometric isomorphisms of finite induced subgraphs extend to automorphisms • indestructible • locally R, but infinite diameter Infinite random geometric graphs Anthony Bonato

Dimensionality • Infinite random geometric graphs Anthony Bonato

Euclidean distance Lemma (BJ, 11) In ℓ 22, every step-isometry is an isometry. • countable dense V is strongly non-Rado if any two such LARG graphs on V are with probability 1 not isomorphic Corollary (BJ, 11) All countable dense sets in ℓ 22 are strongly non-Rado. • non-trivial proof, but ad hoc Infinite random geometric graphs Anthony Bonato

Honeycomb metric Theorem (BJ, 12) Almost all countable dense sets R 2 with the honeycomb metric are strongly non-Rado. Infinite random geometric graphs Anthony Bonato

Enter functional analysis (Balister, Bollobás, Gunderson, Leader, Walters, 17+) Let S be finite-dimensional normed space not isometric to ℓ∞d. Then almost all countable dense sets in S are strongly non-Rado. • proof uses functional analytic tools: – ℓ∞-decomposition – Mazur-Ulam theorem – properties of extreme points in normed spaces Infinite random geometric graphs Anthony Bonato

ℓ∞d are special spaces • ℓ∞d are the only finite-dimensional normed spaces where almost all countable sets are Rado • interpretation: – ℓ∞d is the only space whose geometry is approximated by graph structure Infinite random geometric graphs Anthony Bonato

Questions • classify which countable dense sets are Rado in ℓ∞d • same question, but for finite-dimensional normed spaces. • what about infinite dimensional spaces? Infinite random geometric graphs Anthony Bonato

Infinitely many parallel universes

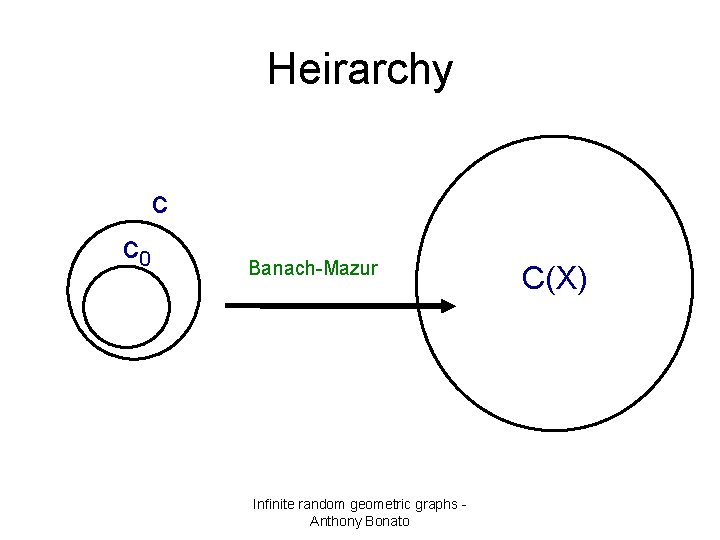
Classical Banach spaces • C(X): continuous function on a compact Hausdorff space X – eg: C[0, 1] • ℓ∞ bounded sequences • c: convergent sequences • c 0: sequences convergent to 0 Infinite random geometric graphs Anthony Bonato

Separability • a normed space is separable if it contains a countable dense set • C[0, 1], c, and c 0 are separable • ℓ∞ and ω1 are not separable Infinite random geometric graphs Anthony Bonato

Heirarchy c c 0 Banach-Mazur Infinite random geometric graphs Anthony Bonato C(X)

Graphs on sequence spaces • fix V a countable dense set in c • LARG model defined analogously to the finite dimensional case • NB: countably infinite graph defined over infinite-dimensional space Infinite random geometric graphs Anthony Bonato

Rado sets in c Lemma (BJ, Quas, 17+): Almost all countable sets in c are dense and idf. Theorem (BJQ, 17+): Almost all countable sets in c are Rado. Ideas of proof: • Lemma: functional analysis • Proof of Theorem somewhat analogous to ℓ∞d • more machinery to deal with the fractional parts of limits of images in back-and-forth argument Infinite random geometric graphs Anthony Bonato

Rado sets in c 0 Theorem (BJ, 17+): There exist countable dense in c 0 that are Rado. • idea: consider the subspace of sequences which are eventually 0 – almost all countable sets in this subspace are dense and idf Infinite random geometric graphs Anthony Bonato

The curious geometry of sequence spaces

Geometric structure: c vs c 0 • c vs c 0 are isomorphic as vector spaces • not isometrically isomorphic: – c contains extreme points • eg: (1, 1, …) – unit ball of c 0 contains no extreme points Infinite random geometric graphs Anthony Bonato

Graph structure: c vs c 0 Theorem (BJ, 17+) 1. The graphs G(c) and G(c 0) are not isomorphic to any GRd. 2. G(c) and G(c 0) are non-isomorphic. • in G(c 0), N≤ 3(x) contains: 3 3 6 Infinite random geometric graphs Anthony Bonato

Interpolating the space from the graph Theorem (BJQ, 17+) Suppose V and W are Banach spaces with dense sets X and Y. If G and H are the 1 -geometric graphs on X and Y (resp) and are isomorphic, then there is a surjective isometry from V to W. • hidden geometry: if we know LARG graphs almost surely, then we can recover the Banach space! Idea - use Dilworth’s theorem: δ-surjective ε-isometries of Banach spaces are uniformly approximated by genuine isometries Infinite random geometric graphs Anthony Bonato

Continuous functions

Dense sets in C[0, 1] (AJQ, 17+) • piecewise linear functions and polynomials – almost all sets are smoothly dense • Brownian motion path functions – almost all sets are IC-dense Infinite random geometric graphs Anthony Bonato

Isomorphism in C[0, 1] Theorem (AJQ, 17+) 1. Smoothly dense sets give rise to a unique isotype of LARG graphs: GR(SD). 2. Almost surely IC-sets give rise to a unique isotype of LARG graphs: GR(ICD). Infinite random geometric graphs Anthony Bonato

Non-isomorphism Theorem (AJQ, 17+) The graphs GR(SD) and GR(ICD) are non-isomorphic. Idea: Dilworth’s theorem and Banach-Stone theorem: isometries on C[0, 1] induce homeomorphisms on [0, 1] Infinite random geometric graphs Anthony Bonato

Questions • “almost all” countable sets in C[0, 1] are Rado? – need a suitable measure of random continuous function • which Banach spaces have Rado sets? • program: interplay of graph structure and the geometry of Banach spaces Infinite random geometric graphs Anthony Bonato

Contact • Web: http: //www. math. ryerson. ca/~abonato/ • Blog: https: //anthonybonato. com/ • • @Anthony_Bonato https: //www. facebook. com/anthony. bonato. 5

Merci!