symmetry symmetry LAVAL LAVAL SHINZOX SHINZOX ININI ININI

















- Slides: 32

symmetry

symmetry

LAVAL

LAVAL

SHINZOX

SHINZOX

ININI

ININI

ININI

ININI

b d p q Dyslexia…

bd pq

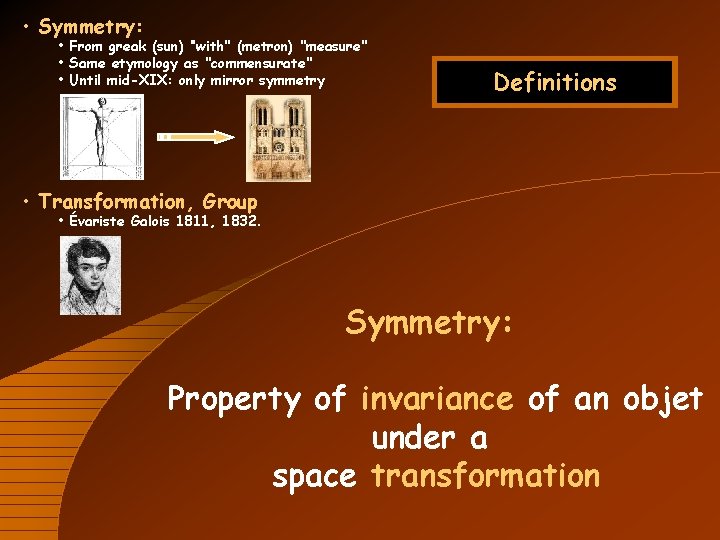
• Symmetry: • From greak (sun) ‘’with" (metron) "measure" • Same etymology as "commensurate" • Until mid-XIX: only mirror symmetry Definitions • Transformation, Group • Évariste Galois 1811, 1832. Symmetry: Property of invariance of an objet under a space transformation

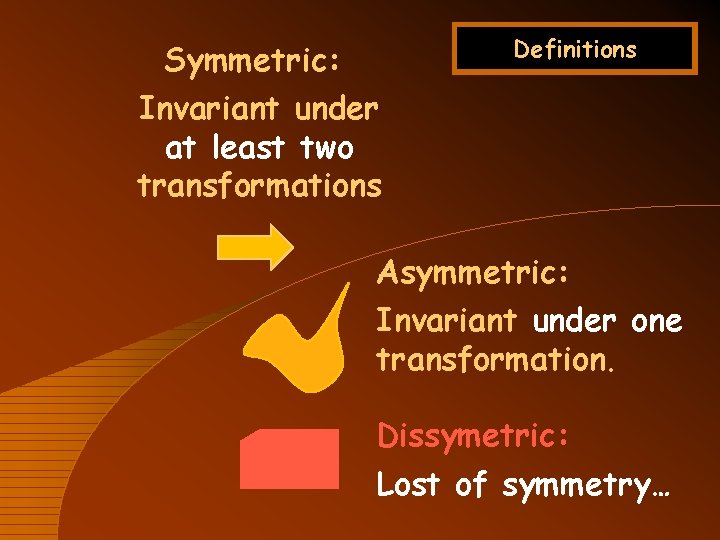
Definitions Symmetric: Invariant under at least two transformations Asymmetric: Invariant under one transformation. Dissymetric: Lost of symmetry…

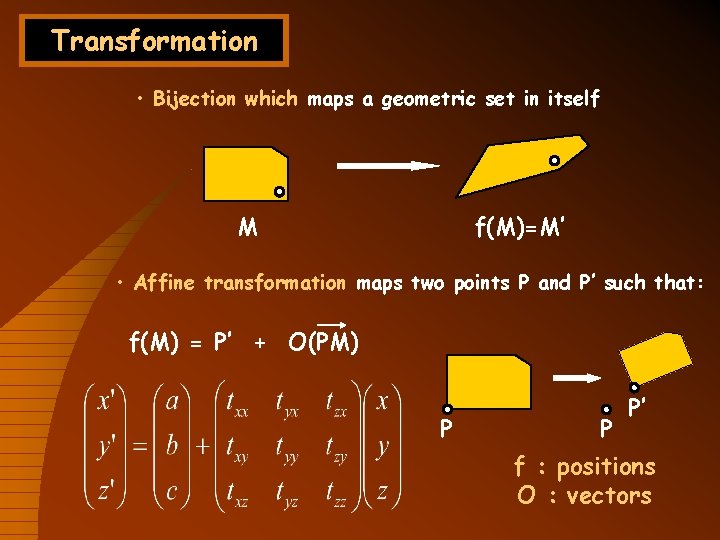
Transformation • Bijection which maps a geometric set in itself M f(M)=M’ • Affine transformation maps two points P and P’ such that: f(M) = P’ + O(PM) P P P’ f : positions O : vectors

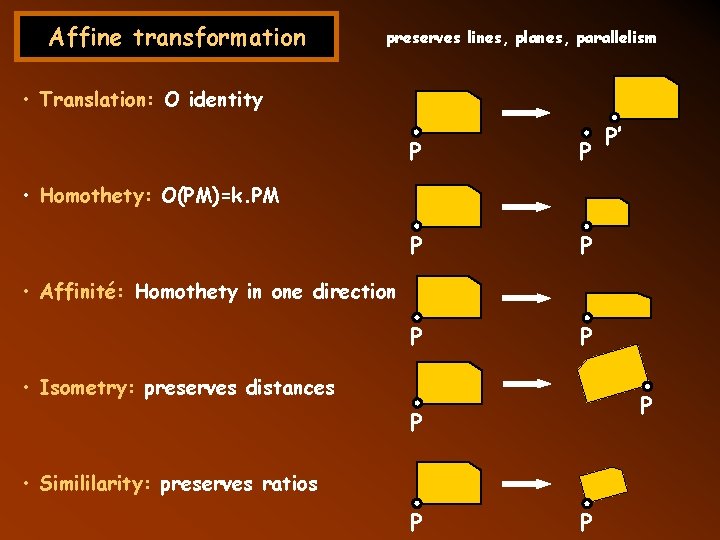
Affine transformation preserves lines, planes, parallelism • Translation: O identity P P P P’ • Homothety: O(PM)=k. PM • Affinité: Homothety in one direction • Isometry: preserves distances P P • Simililarity: preserves ratios P P

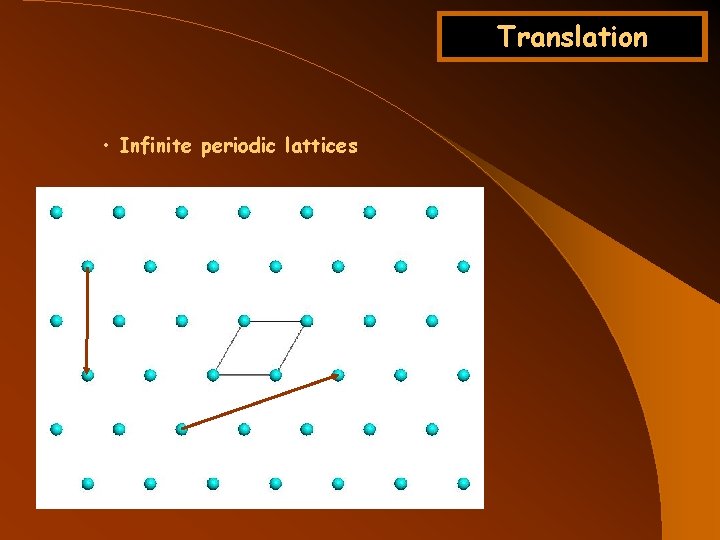
Translation • Infinite periodic lattices

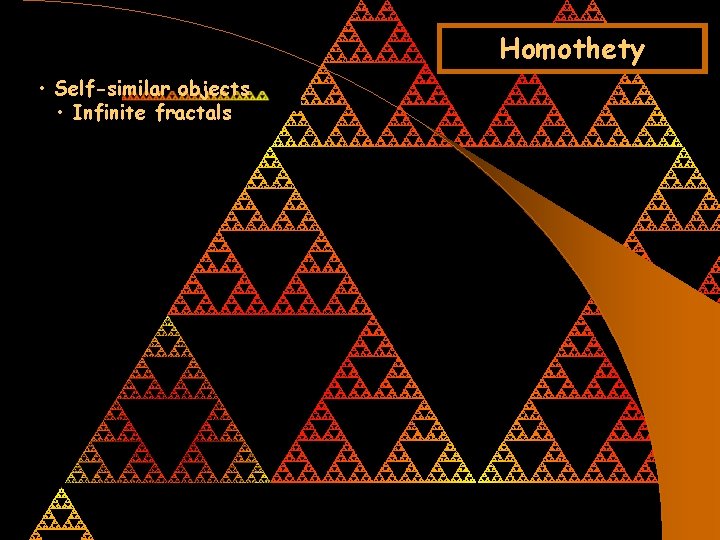
Homothety • Self-similar objects • Infinite fractals

Similitude Infinite fractal Logarithmic spiral (r=aebq) q -> q+q’ r -> re-bq’ q’

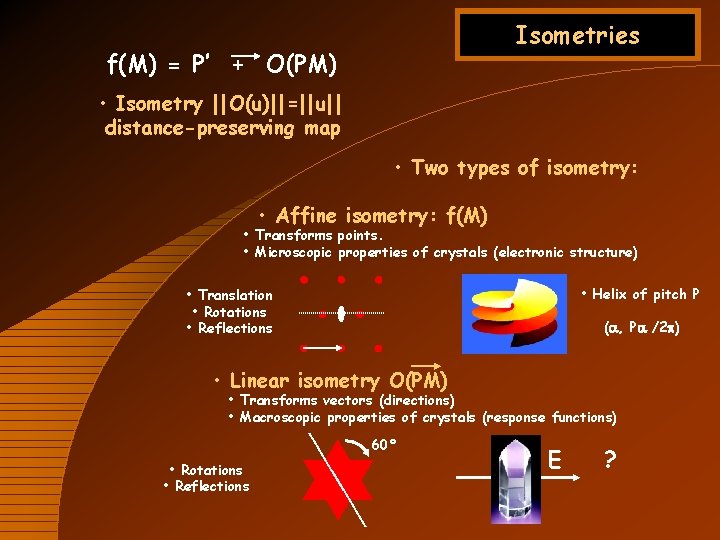
Isometries f(M) = P’ + O(PM) • Isometry ||O(u)||=||u|| distance-preserving map • Two types of isometry: • Affine isometry: f(M) • Transforms points. • Microscopic properties of crystals (electronic structure) • Helix of pitch P • Translation • Rotations • Reflections (a, Pa /2 p) • Linear isometry O(PM) • Transforms vectors (directions) • Macroscopic properties of crystals (response functions) 60° • Rotations • Reflections E ?

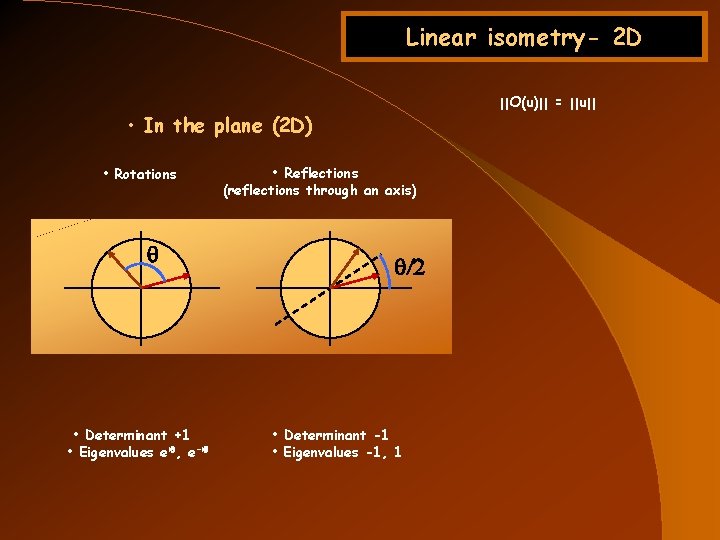
Linear isometry- 2 D ||O(u)|| = ||u|| • In the plane (2 D) • Rotations q • Determinant +1 • Eigenvalues eiq, e-iq • Reflections (reflections through an axis) q/2 • Determinant -1 • Eigenvalues -1, 1

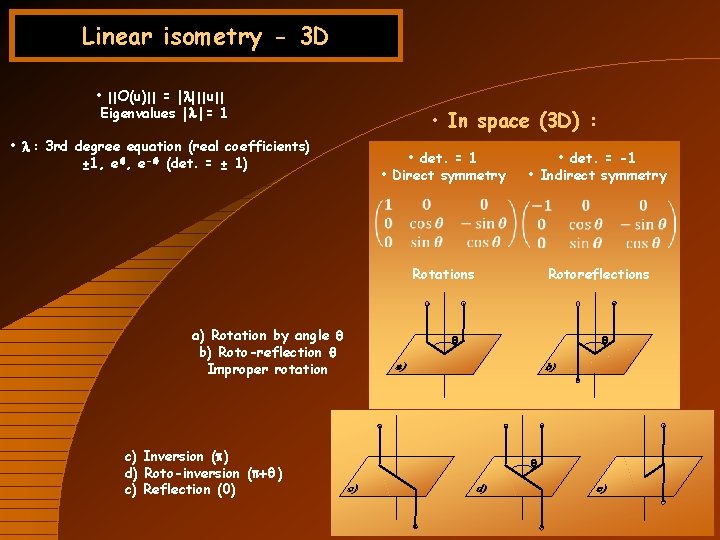
Linear isometry - 3 D • ||O(u)|| = |l| ||u|| Eigenvalues |l | = 1 • l : 3 rd degree equation (real coefficients) ± 1, eiq, e-iq (det. = ± 1) • In space (3 D) : • det. = 1 • Direct symmetry • det. = -1 • Indirect symmetry Rotoreflections Rotations a) Rotation by angle q b) Roto-reflection q Improper rotation c) Inversion (p) d) Roto-inversion (p+q ) c) Reflection (0) q q q

Stereographic projection • To represent directions preserves angles on the sphere NN Direction OM M P’ O P P’ M’ P S P, projection of OM : Intersection of SM and equator • Conform transformation (preserves angles locally) but not affine

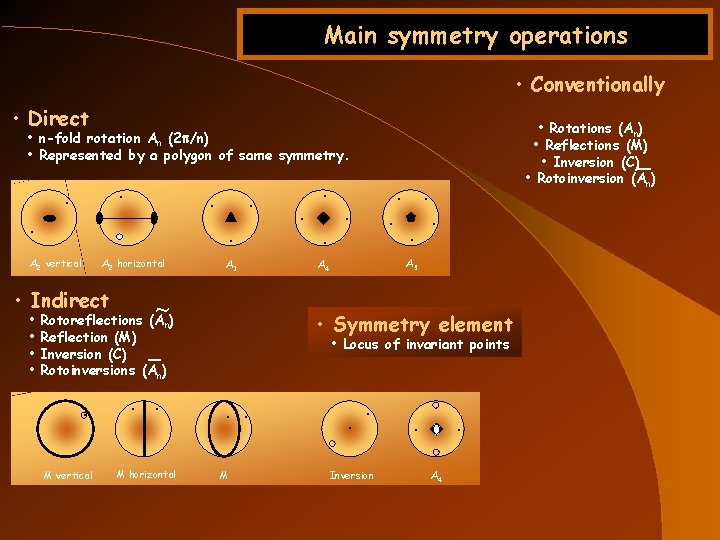
Main symmetry operations • Conventionally • Direct • Rotations (An) • Reflections (M) • Inversion (C) • Rotoinversion (An) • n-fold rotation An (2 p/n) • Represented by a polygon of same symmetry. . . . A 2 vertical A 2 horizontal • Indirect • • A 3 ~ M vertical M horizontal . . . A 5 A 4 • Locus of invariant points _ . . . • Symmetry element Rotoreflections (An) Reflection (M) Inversion (C) Rotoinversions (An) . . . _ . . M . . Inversion . . A 4

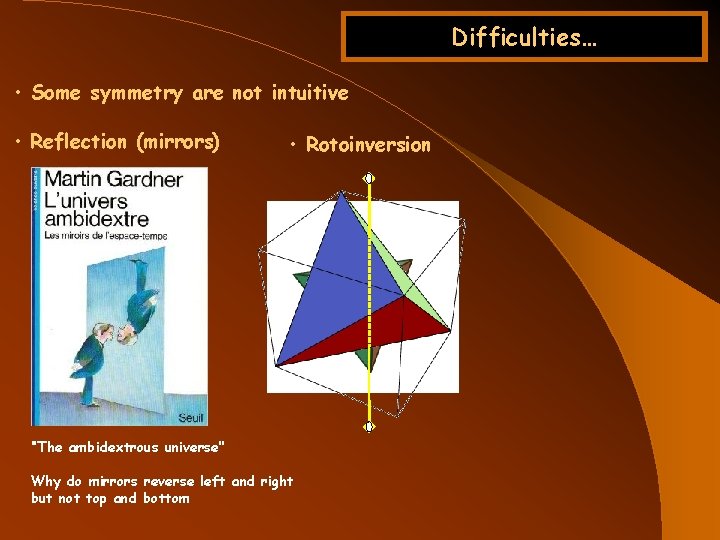
Difficulties… • Some symmetry are not intuitive • Reflection (mirrors) • Rotoinversion ‘’The ambidextrous universe’’ Why do mirrors reverse left and right but not top and bottom

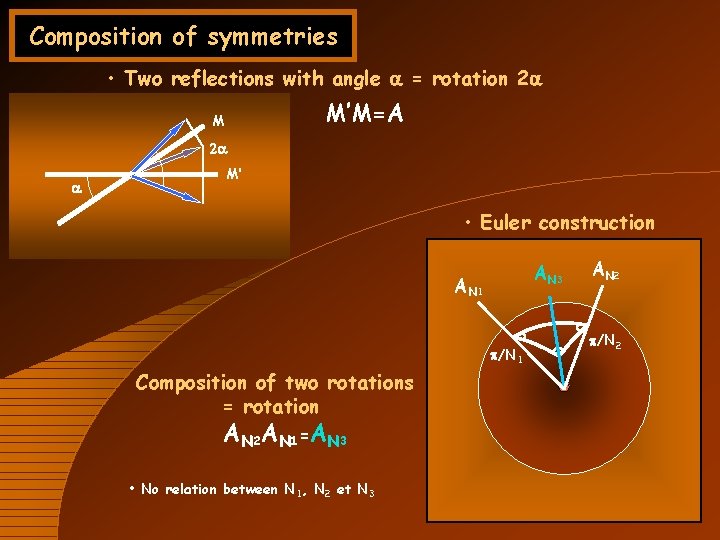
Composition of symmetries • Two reflections with angle a = rotation 2 a M’M=A M 2 a a M’ • Euler construction AN 3 AN 1 p/N 1 Composition of two rotations = rotation A N 2 A N 1= A N 3 • No relation between N 1, N 2 et N 3 AN 2 p/N 2

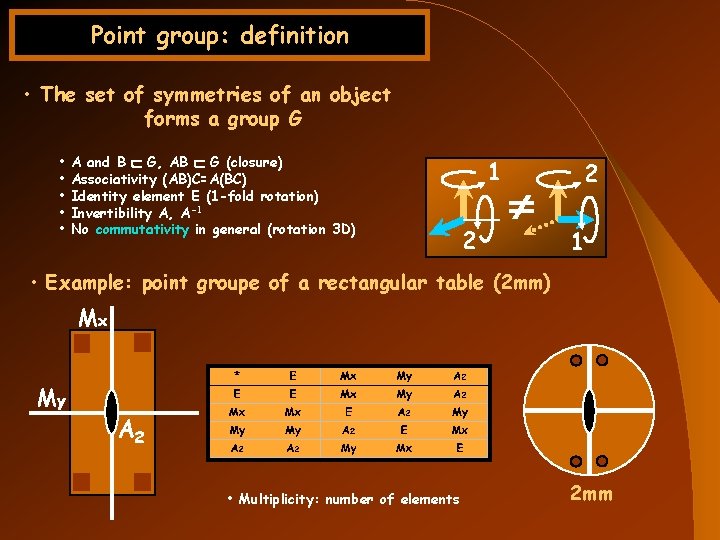
Point group: definition • The set of symmetries of an object forms a group G • • • A and B G, AB G (closure) Associativity (AB)C=A(BC) Identity element E (1 -fold rotation) Invertibility A, A-1 No commutativity in general (rotation 3 D) 1 2 2 1 • Example: point groupe of a rectangular table (2 mm) Mx My A 2 • Multiplicity: number of elements 2 mm

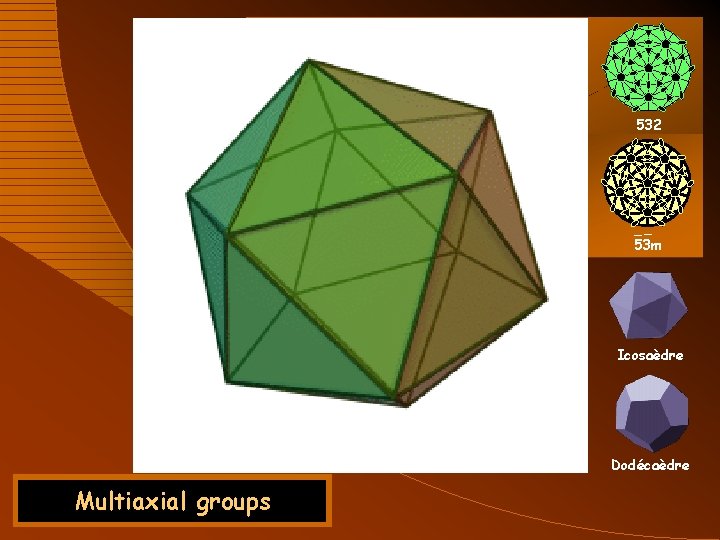
Composition of rotations Constraints AN 1 p/N 1 AN 3 AN 2 p/N 2 234 Spherical triangle, angles verifies: 22 N (N>2), 233, 234, 235 Dihedral groups Multiaxial groups

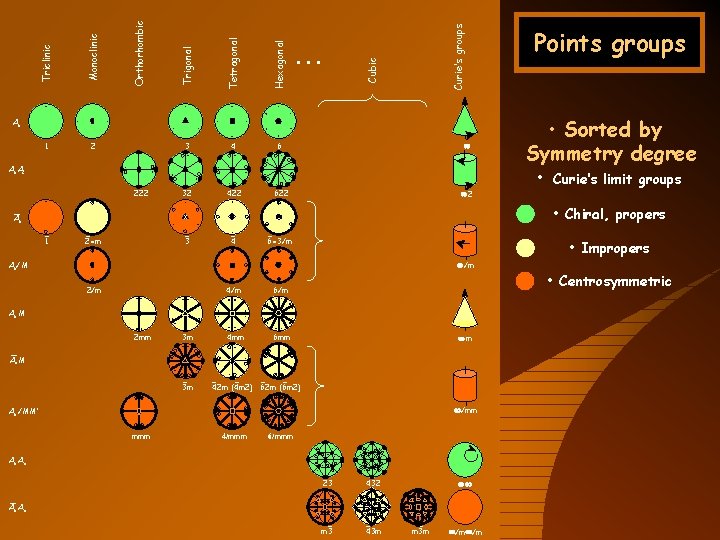
Curie’s groups Cubic Hexagonal Tetragonal Trigonal Orthorhombic Monoclinic Triclinic . . . An 1 2 3 4 6 ¥ 32 422 622 ¥ 2 An A 2 222 Points groups • Sorted by Symmetry degree • Curie‘s limit groups • Chiral, propers _ An _ 1 _ 2=m _ 3 _ 4 _ 6=3/m • Impropers An/M ¥ /m 2/m 4/m 6/m 4 mm 6 mm An M 2 mm 3 m ¥m _ An M _ 3 m _ _ 42 m (4 m 2) 62 m (6 m 2) ¥ /mm An /MM’ mmm 4/mmm 6/mmm An An’ 23 432 _ m 3 _ 43 m ¥¥ _ An An’ _ m 3 m ¥/m¥/m • Centrosymmetric

23 _ m 3 Multiaxial groups 532 432 _ _ __ 43 m m 3 m 53 m Tétraèdre Octaèdre Icosaèdre Cube Dodécaèdre

Points group: Notations • Hermann-Mauguin (International notation - 1935) • Generators (not minimum) • Symmetry directions • Reflection ( - ): defined by the normal to the plane Primary Direction: higher-order symmetry Secondary directions : lower-order 4 2 2 mmm Notation réduite 4 mm m Tertiary directions : lowest-order • Schönflies : Cn, Dnh

Les 7 groupes limites de Pierre Curie Cône tournant Vecteur axial + polaire Cylindre tordu Tenseur axial d’ordre 2 Cylindre tournant Vecteur axial (H) Cône Vecteur polaire (E, F) Cylindre Tenseur polaire d’ordre 2 (susceptibilité) Sphère tournante Scalaire axial (chiralité) Sphère Scalaire polaire (pression, masse) ¥ ¥ 2 ¥ /m ¥m ¥ /mm ¥¥ ¥ /m
 Alfa laval sustainability report
Alfa laval sustainability report Crds laurentides
Crds laurentides Quentin martin laval
Quentin martin laval Why did the hoare laval pact fail
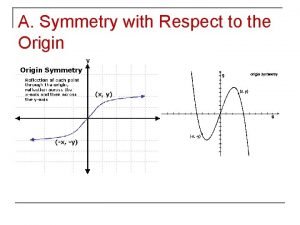
Why did the hoare laval pact fail Graph origin symmetry
Graph origin symmetry Symmetry powerpoint
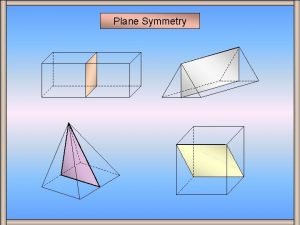
Symmetry powerpoint Cylindrical tolerance zone
Cylindrical tolerance zone Chapter 24 section 3 sponges and cnidarians
Chapter 24 section 3 sponges and cnidarians Parallelogram axis of symmetry
Parallelogram axis of symmetry Symmetry definition in maths
Symmetry definition in maths Odd quarter wave symmetry
Odd quarter wave symmetry Tape worm class
Tape worm class Symmetrical porifera
Symmetrical porifera Hfss master slave boundary
Hfss master slave boundary Spherical symmetry zoology
Spherical symmetry zoology Arthropoda symmetry
Arthropoda symmetry Types of symmetry
Types of symmetry Direct product tables
Direct product tables Tutorial of symmetry
Tutorial of symmetry Sea star cephalization
Sea star cephalization Y = sinx + 1
Y = sinx + 1 Quark lepton symmetry
Quark lepton symmetry Neumann principle symmetry
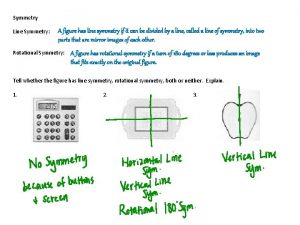
Neumann principle symmetry 2 fold symmetry
2 fold symmetry Test for symmetry
Test for symmetry Radial symmetry cnidaria
Radial symmetry cnidaria Slide to doc downloader
Slide to doc downloader Symmetry of worms
Symmetry of worms Mandala radial symmetry
Mandala radial symmetry Origin symmetry examples
Origin symmetry examples How to draw a bookshelf in two point perspective
How to draw a bookshelf in two point perspective Gauss law
Gauss law Transpose symmetry asymptotic notation
Transpose symmetry asymptotic notation