ANALYSIS AND DESIGN OF ALGORITHMS CSEN 707 Tutorial

ANALYSIS AND DESIGN OF ALGORITHMS [CSEN 707] Tutorial 2 By: Mariham Wasfy

Content § Growth of functions § Asymptotic Notation § Comparison of function

GROWTH OF FUNCTIONS

Growth of functions The order of growth of the running time of an algorithm, gives a simple characterization of the algorithm’s efficiency and also allows us to compare the relative performance of alternative Algorithms (what will happen when system grows).

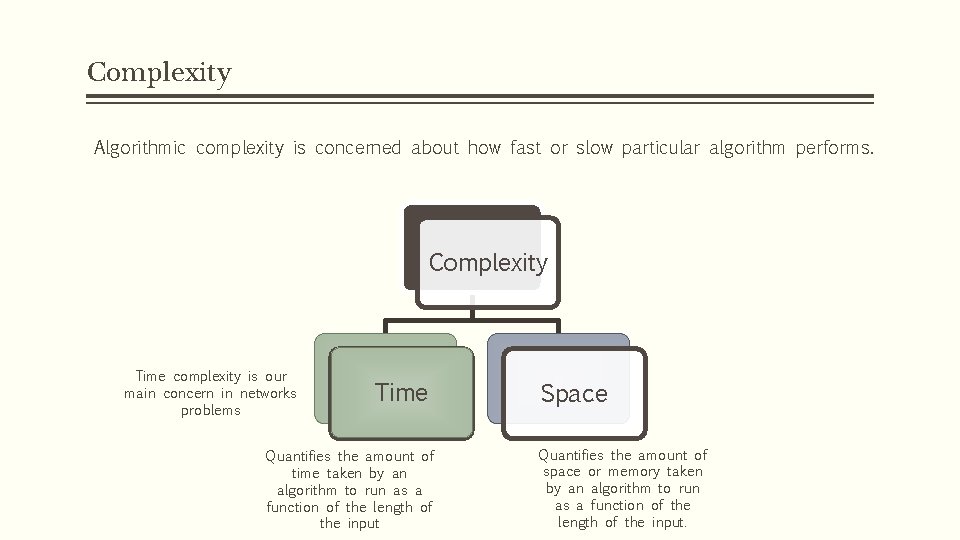
Complexity Algorithmic complexity is concerned about how fast or slow particular algorithm performs. Complexity Time complexity is our main concern in networks problems Time Quantifies the amount of time taken by an algorithm to run as a function of the length of the input Space Quantifies the amount of space or memory taken by an algorithm to run as a function of the length of the input.

ASYMPTOTIC NOTATIONS

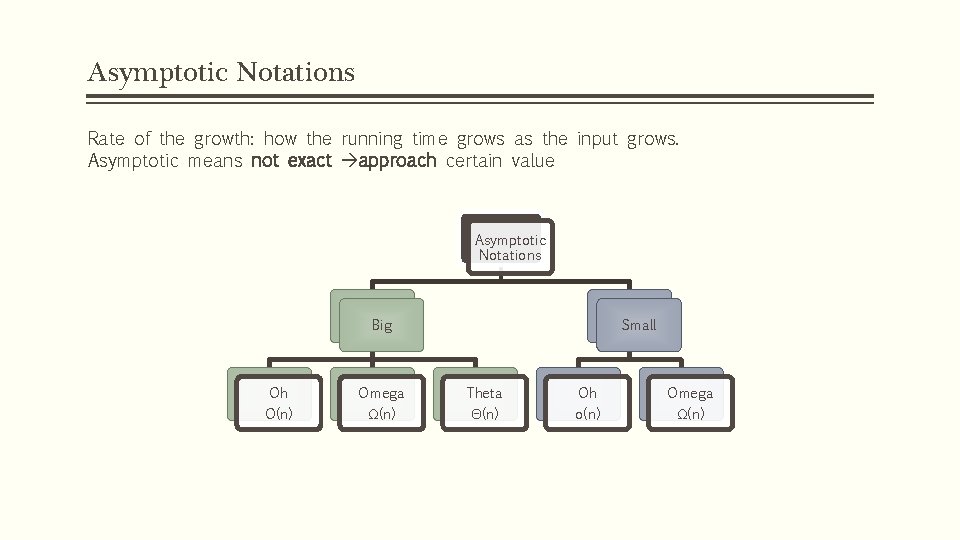
Asymptotic Notations Rate of the growth: how the running time grows as the input grows. Asymptotic means not exact approach certain value Asymptotic Notations Big Small Oh Omega Theta Oh Omega O(n) Ω(n) Θ(n) o(n) Ω(n)

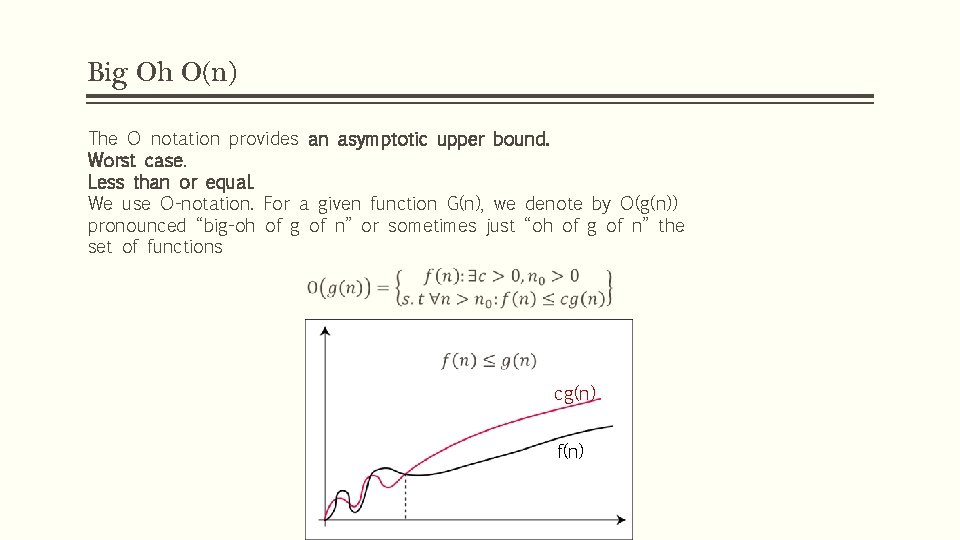
Big Oh O(n) The O notation provides an asymptotic upper bound. Worst case. Less than or equal. We use O-notation. For a given function G(n), we denote by O(g(n)) pronounced “big-oh of g of n” or sometimes just “oh of g of n” the set of functions cg(n) f(n)

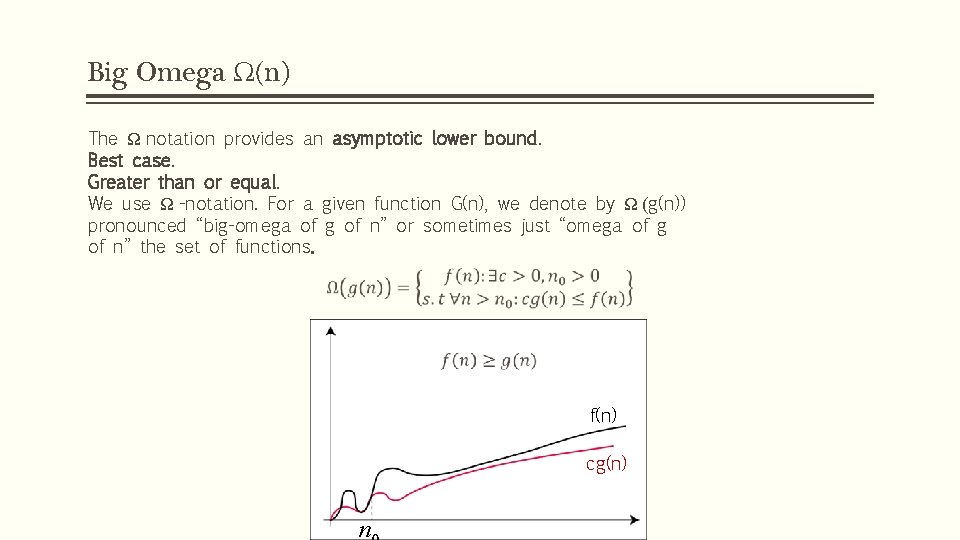
Big Omega Ω(n) The Ω notation provides an asymptotic lower bound. Best case. Greater than or equal. We use Ω -notation. For a given function G(n), we denote by Ω (g(n)) pronounced “big-omega of g of n” or sometimes just “omega of g of n” the set of functions. f(n) cg(n) n

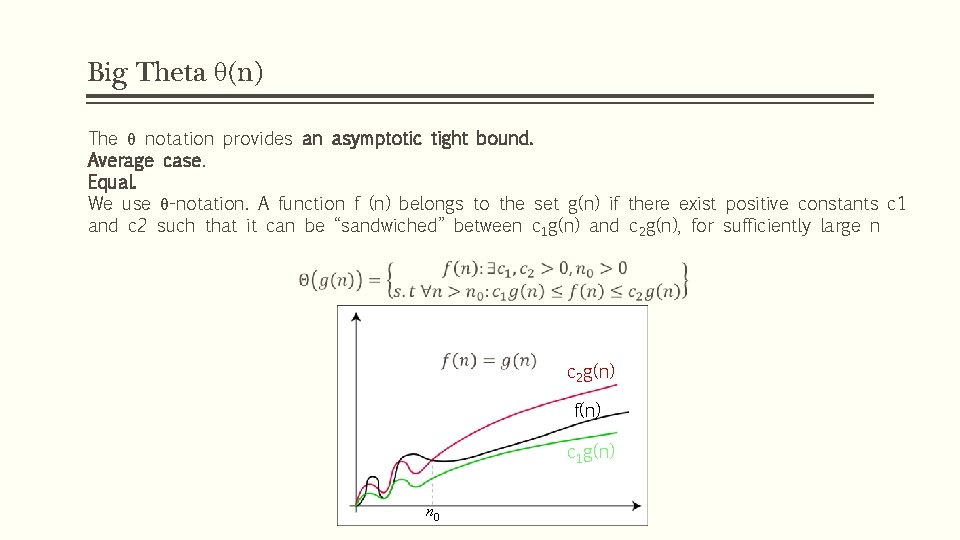
Big Theta θ(n) The θ notation provides an asymptotic tight bound. Average case. Equal. We use θ-notation. A function f (n) belongs to the set g(n) if there exist positive constants c 1 and c 2 such that it can be “sandwiched” between c 1 g(n) and c 2 g(n), for sufficiently large n c 2 g(n) f(n) c 1 g(n) n 0

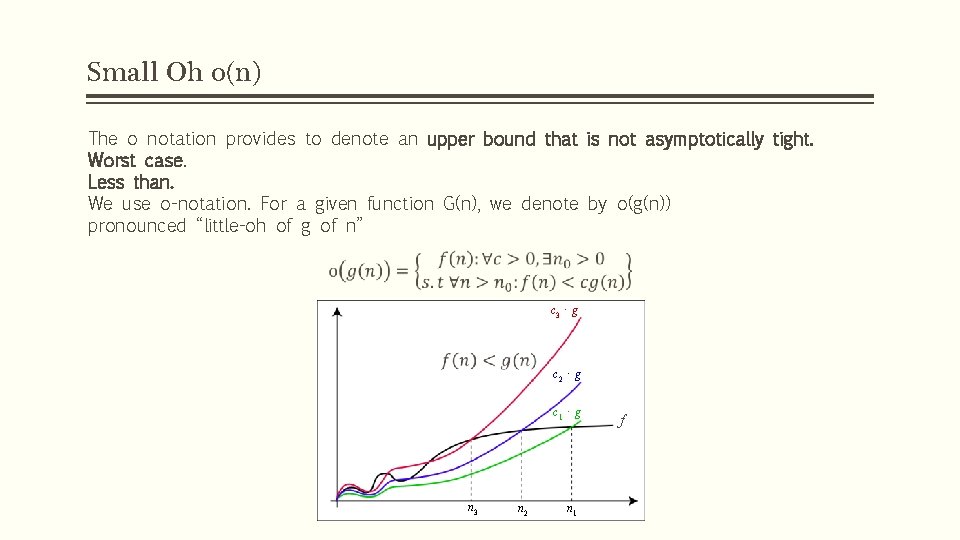
Small Oh o(n) The o notation provides to denote an upper bound that is not asymptotically tight. Worst case. Less than. We use o-notation. For a given function G(n), we denote by o(g(n)) pronounced “little-oh of g of n” c 3 ⋅ g c 2 ⋅ g c 1 ⋅ g n 3 n 2 n 1 f

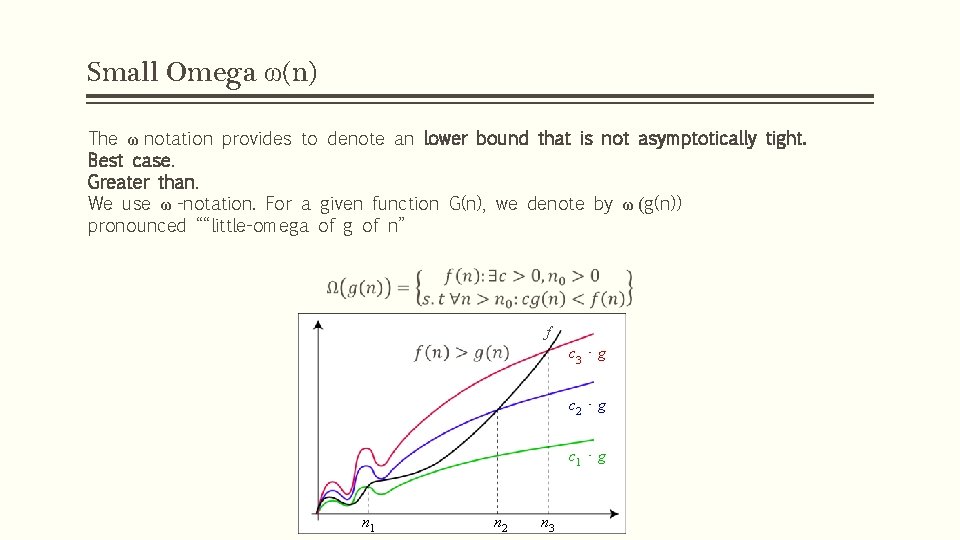
Small Omega ω(n) The ω notation provides to denote an lower bound that is not asymptotically tight. Best case. Greater than. We use ω -notation. For a given function G(n), we denote by ω (g(n)) pronounced ““little-omega of g of n” f c 3 ⋅ g c 2 ⋅ g c 1 ⋅ g n 1 n 2 n 3

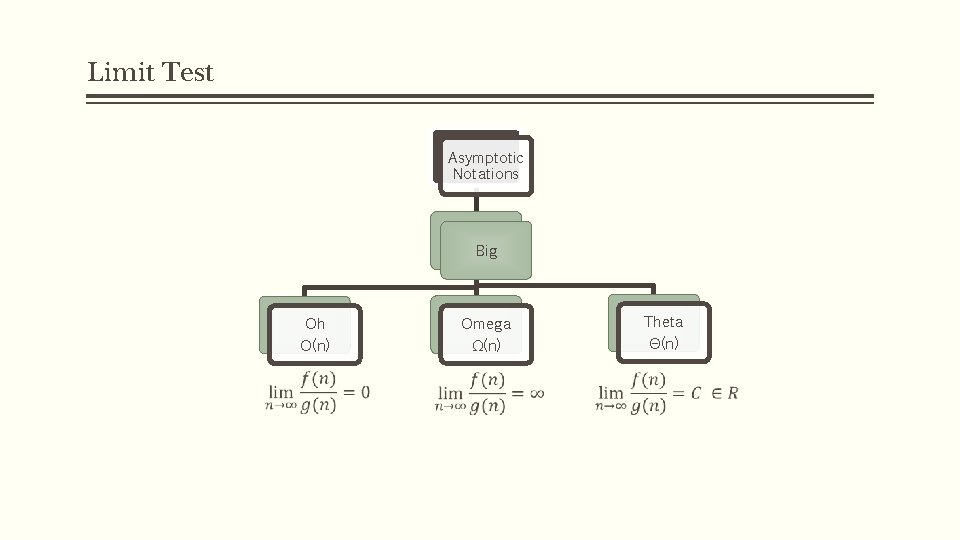
Limit Test Asymptotic Notations Big Theta Θ(n) Omega Ω(n) Oh O(n)

COMPARISON OF FUNCTION

Transitivity

Relativity

Symmetry

Transpose Symmetry

Theorem