COMP 171 Data Structures and Algorithms Tutorial 2






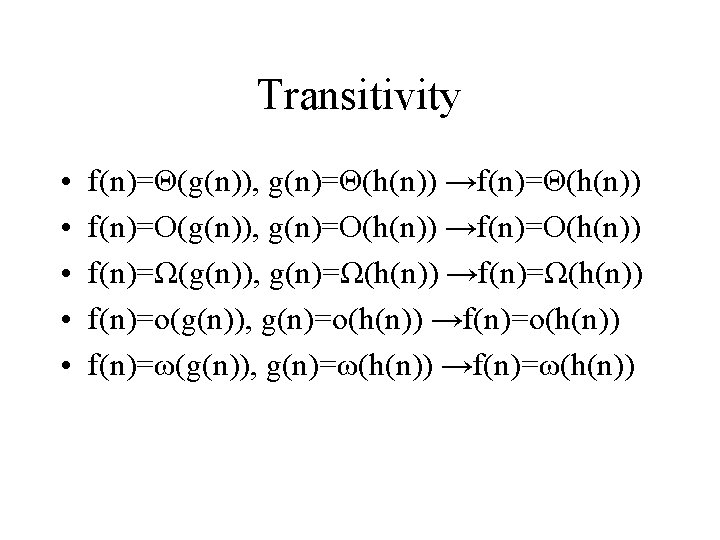









- Slides: 18

COMP 171 Data Structures and Algorithms Tutorial 2 Analysis of algorithms

Ο-notation • Big-Oh • f(n) =Ο(g(n)) • Ο(g(n)) = {f(n) : there exist positive constants c and n 0 such that 0≦f(n)≦cg(n) for all n≧n 0} • Upper bound • Worst-case running time

ο-notation • Little-Oh • f(n) =ο(g(n)) • ο(g(n)) = {f(n) : for any positive constants c and n 0 such that 0≦f(n)<cg(n) for all n≧n 0} • Non-tight upper bound

Ω-notation • Big-Omega • f(n) =Ω(g(n)) • Ω(g(n)) = {f(n) : there exist positive constants c and n 0 such that 0 ≦cg(n)≦f(n) for all n≧n 0} • Lower bound • Best-case running time

ω-notation • Little-Omega • f(n) = ω(g(n)) • ω(g(n)) = {f(n) : for any positive constants c and n 0 such that 0 ≦cg(n)<f(n) for all n≧n 0} • Non-tight lower bound

Θ-notation • Theta • f(n) =Θ(g(n)) • Θ(g(n)) = {f(n) : there exist positive constants c 1, c 2 and n 0 such that 0≦c 1 g(n)≦f(n)≦c 2 g(n) for all n≧n 0} • Tight bound

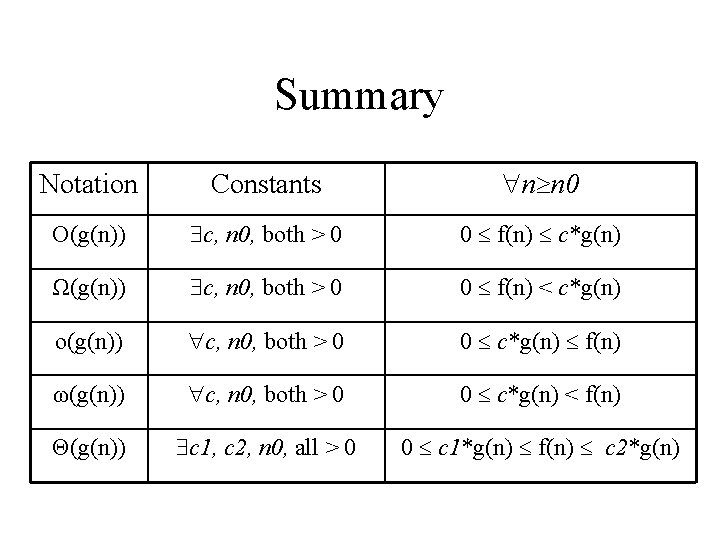
Summary Notation Constants n n 0 Ο(g(n)) c, n 0, both > 0 0 f(n) c*g(n) Ω(g(n)) c, n 0, both > 0 0 f(n) < c*g(n) ο(g(n)) c, n 0, both > 0 0 c*g(n) f(n) ω(g(n)) c, n 0, both > 0 0 c*g(n) < f(n) Θ(g(n)) c 1, c 2, n 0, all > 0 0 c 1*g(n) f(n) c 2*g(n)
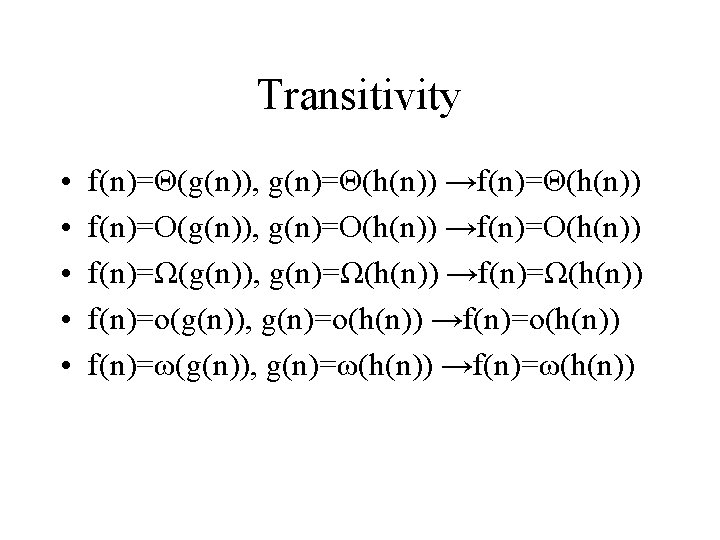

Reflexivity, Symmetry & Transpose Symmetry • • • f(n)=Θ(f(n)) f(n)=Ο(f(n)) f(n)=Ω(f(n)) f(n)=Θ(g(n)) if and only if g(n)=Θ(f(n)) f(n)=Ο(g(n)) if and only if g(n)=Ω(f(n)) f(n)=ο(g(n)) if and only if g(n)=ω(f(n))

Selection Sort • Input: Array A of Size n • Output: A sorted array A • Algorithm: Find the smallest element of A and exchanging it with the element in A[1]. Then find the second smallest element of A and exchange it with A[2]. Continue for the first n-1 elements in A.

• e. g. {5, 2, 4, 7, 3} • Input: {5, 2, 4, 7, 3} • 1 st iteration: {2, 5, 4, 7, 3} • 2 nd iteration: {2, 3, 4, 7, 5} • 3 rd iteration: {2, 3, 4, 7, 5} • 4 th iteration: {2, 3, 4, 5, 7} • Output: {2, 3, 4, 5, 7}

Sorted Part Unsorted Part • 1: Find the smallest(m) in the unsorted part h m m h • 2: Swap with h • 3: Put m into the sorted part m • 4: Back to 1 until unsorted part is size 1

for i ← range 1 min = value min_pos = value for j ← range 2 find min end for j swap(value, value) end for i

for i ← 1 to n-1 min = infinity min_pos = 0 for j ← i to n if A[j] < min then min = A[j] min_pos = j end if end for j swap(A[i], A[min_pos]) end for i

for i ← 1 to n-1 min = infinity min_pos = 0 for j ← i to n if A[j] < min then min = A[j] min_pos = j end if end for j swap(A[i], A[min_pos]) end for i O(1 ) O(n )

• Ο(n 2) • Ω(n 2)? • Θ(n 2)? • In class exercise: – Improve the algorithm so it can achieve: • Ο(n 2) • Ω(n) – Given a sorted input sequence, which sorting algorithm(s) can achieve Ω(n)?

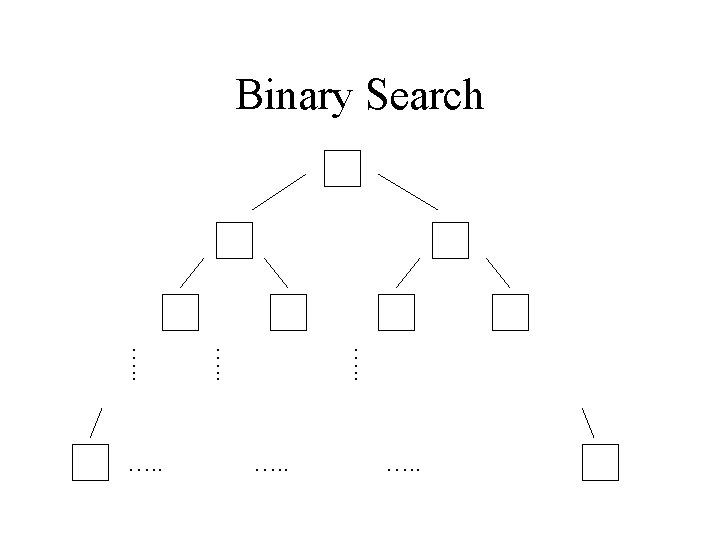
Binary Search …. .

• • • If tree height is k The number of elements is 2 k+1 -1=n The number of comparison is at most k+1 = log 22 k+1 =log 2 ( n+1 ) Ο(㏒ n)