Radial Symmetry Mandala Get your sketchbooks Vocabulary Radial

Radial Symmetry: Mandala Get your sketchbooks

Vocabulary • Radial Symmetry (or Radial Balance) - a type of balance in which all elements radiate out from a center point. • Mandala – an abstract circular design that has one center point, from which extends an array of symbols, shapes and forms.

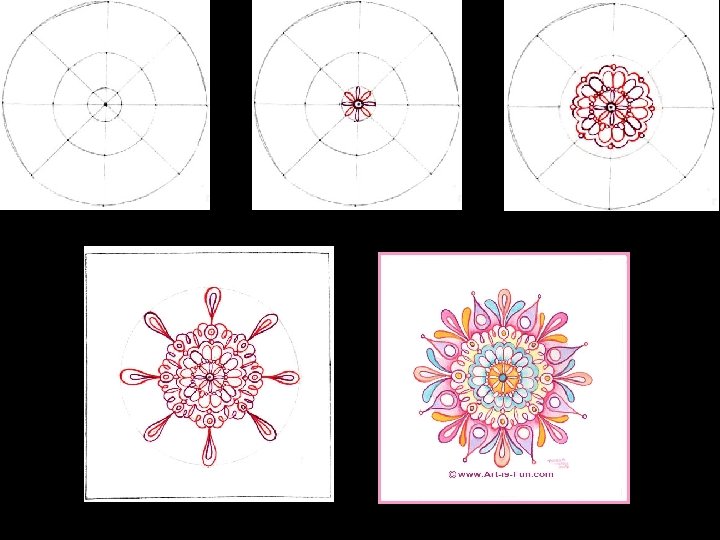
Mandala: Step by Step • Draw 1 inch border around paper. • Find center point of each edge. • Draw straight lines to find center point of the Mandala. • Use compass to draw circle. Multiple circles. • Start in the center and work out toward the edges. • Experiment with patterns and shapes. • Personalize it! Make it meaningful to you.

Pointless Compass

Overview • Brainstorm and sketch ideas in sketchbook. • Finalize Mandala idea and transfer to 12 x 12 paper. • *Optional: Outline design in technical pen. • Mandala will be colored in with colored pencil.

Today: Sketchbook • Start brainstorming Mandala designs. • Experiment with shapes, lines, patterns, and symbols. • Play with the compass. • Figure out ways to make it personal.

Colored Pencils Soft-core Colored Pencils Verithin Colored Pencils

Colored Pencils - Tips • Apply in thin layers to build up color values. • Colors can be blended together. • DO NOT drop pencils on the floor or drum with them on the tabletops. • They are expensive. Treat them with respect.

Today: • • Finalize Mandala design. Make it personal to you. Get it approved. Transfer Mandala design to 12 x 12 final paper.