Reti di Petri Condizioni e eventi Gli eventi

Reti di Petri

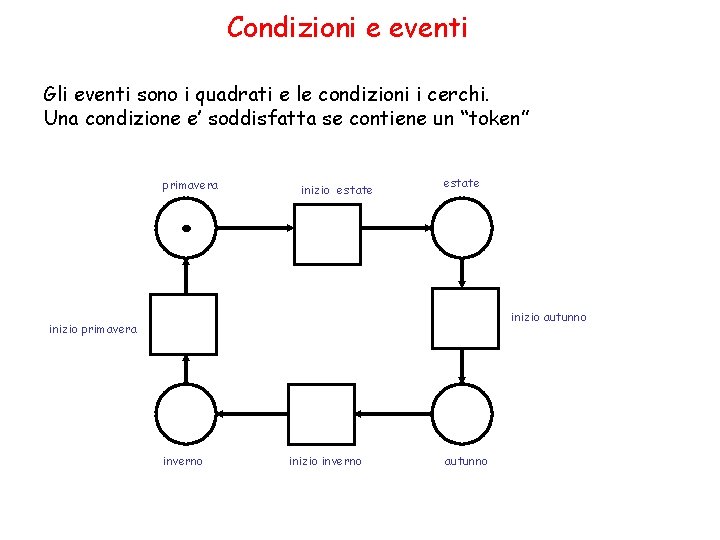
Condizioni e eventi Gli eventi sono i quadrati e le condizioni i cerchi. Una condizione e’ soddisfatta se contiene un “token” . primavera inizio estate inizio autunno inizio primavera inverno inizio inverno autunno

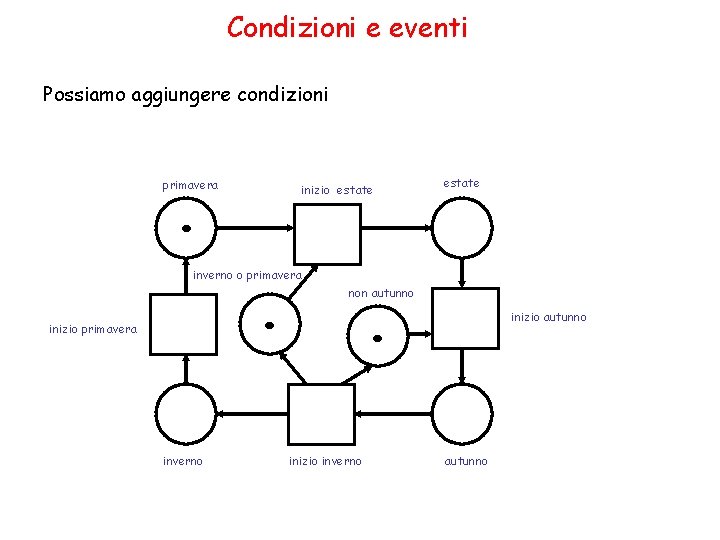
Condizioni e eventi Possiamo aggiungere condizioni . primavera inizio estate inverno o primavera . inizio primavera inverno estate . non autunno inizio inverno inizio autunno

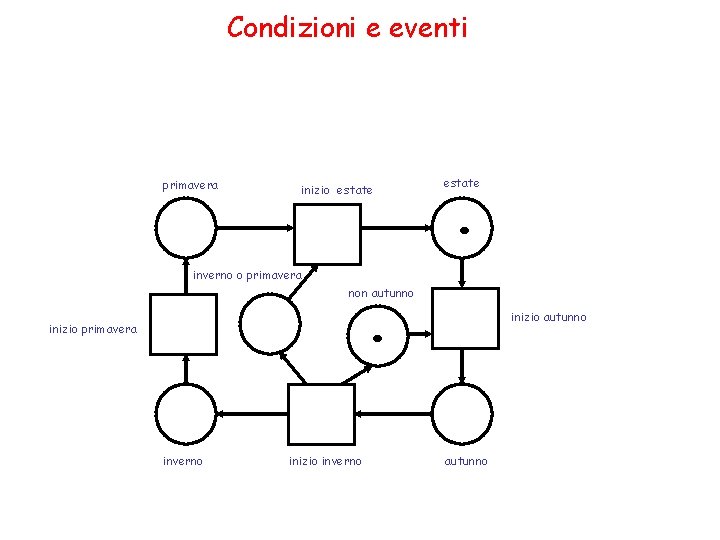
Condizioni e eventi primavera inizio estate inverno o primavera . estate . non autunno inizio primavera inverno inizio autunno

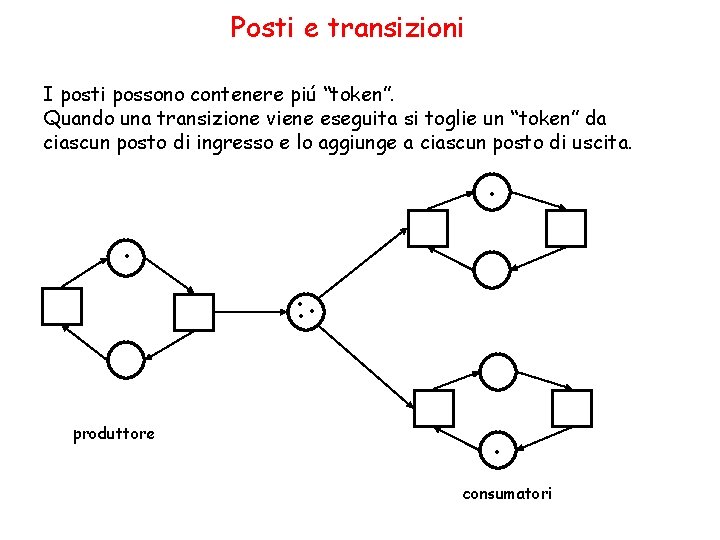
Posti e transizioni I posti possono contenere piú “token”. Quando una transizione viene eseguita si toglie un “token” da ciascun posto di ingresso e lo aggiunge a ciascun posto di uscita. . . produttore . consumatori

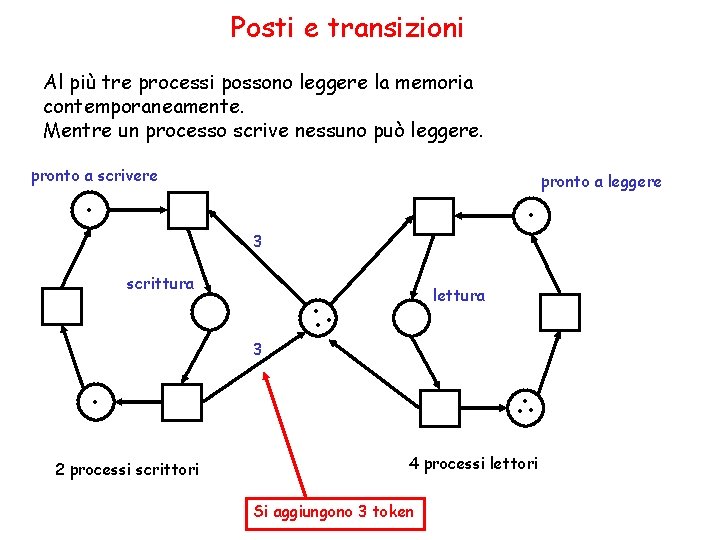
Posti e transizioni Al più tre processi possono leggere la memoria contemporaneamente. Mentre un processo scrive nessuno può leggere. pronto a scrivere . . 3 scrittura . . . lettura 3 . . 2 processi scrittori 4 processi lettori Si aggiungono 3 token pronto a leggere

Definizioni di base (1) Una tripla N = (S, T, F) è chiamata rete se e solo se: 1) S e T sono insiemi disgiunti (gli elementi di S sono chiamati S -elementi, gli elementi di T sono chiamati T-elementi) 2) F (S T) (T S) è una relazione binaria, chiamata la relazione di flusso di N. Graficamente S-elementi sono rappresentati come cerchi e Telementi come quadrati, la relazione di flusso è rappresentata da archi orientati che connettono cerchi e quadrati Notazione. Sia N = (S, T, F) una rete. Denotiamo le componenti come SN, TN, FN e scriviamo anche N per S T. Sia N una rete. Per x N. x = { y | y F x} è chiamato il preset di x N. x = { y | x FN y} è chiamato il postset di x Per X N sia. X = x X. x e X. = x X x. .

Definizioni di base (2) Per x, y N si ha x . y y x. . Una coppia (s, t) SN TN è un self-loop se e solo se s FN t and t FN s. Una rete N è pura se FN non contiene self-loop. Un elemento x N è isolato se e solo se. x x. = . Una rete N è semplice se elementi distinti non hanno lo stesso preset e postset, ossia se, per ogni x, y N, . x =. y and x. = y. => x = y.

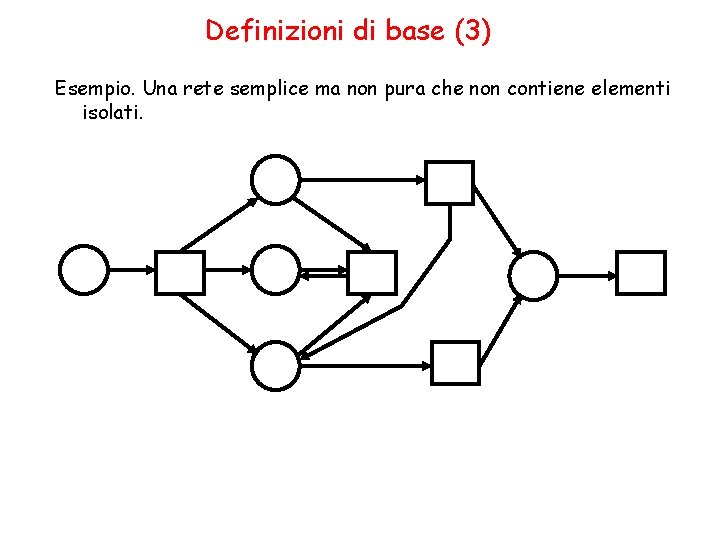
Definizioni di base (3) Esempio. Una rete semplice ma non pura che non contiene elementi isolati.

Definizioni di base (4) Siano N e N’ due reti. Data una biiezione b : N N’ chiamiamo N e N’ b-isomorfe se e solo se s SN b(s) SN ’ and x FN y b(x) FN ’ b(y). Questo implica t TN b(t) TN ’. Due reti N e N’ sono isomorfe se e solo se sono isomorfe per qualche funzione b. Rappresentazioni grafiche in cui gli elementi non hanno un nome rappresentano reti a meno di isomorfismo.

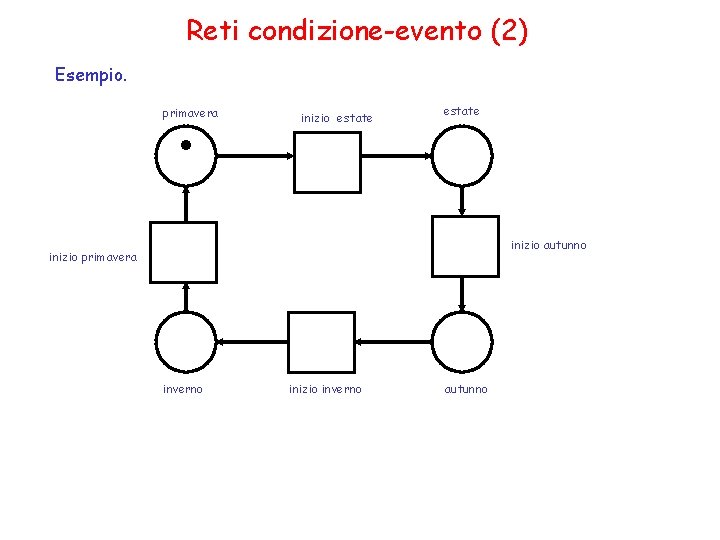
Reti condizione-evento (1) Gli S-elementi rappresentano condizioni e indichiamo con B il loro insieme, i T-elementi rappresentano eventi e indichiamo con E il loro insieme. L’insieme delle condizioni che valgono in una configurazione è un caso. Sia N = (B, E, F) una rete. 1) un sottoinsieme c B è un caso 2) sia e E e c B; e ha una concessione in c (è c-abilitato) se e solo se. e c and e. c = (assenza di contatto) 3) sia e E, sia c B, e sia c-abilitato. Allora c’ = (c. e) e. è il caso successore di c sotto e ( c’ risulta dall’occorrenza di e nel caso c) e scriviamo c [e > c’. Notazione. Nella rappresentazione grafica si indica che una condizione vale ponendo una marca nel cerchio che la rappresenta.

Reti condizione-evento (2) Esempio. . primavera inizio estate inizio autunno inizio primavera inverno inizio inverno autunno

Reti condizione-evento (3) Eventi i cui preset e postset sono disgiunti possono essere combinati in un passo. Sia N = (B, E, F) una rete. Un insieme di eventi G E è distaccato (detached) se e solo se per ogni e 1, e 2 G e 1 differente da e 2 =>. e 1 . e 2 = = e 1. e 2. . Siano c, c’ casi di N e sia G distaccato. Allora g è un passo da c a c’, ossia c [G > c’ se e solo se ogni evento e G è abilitato e c’ = (c. G) G. . Lemma. Sia N una rete, sia G EN distaccato e siano c, c’ casi di N. Allora c [G > c’ cc’ =. G and c’c = G. .

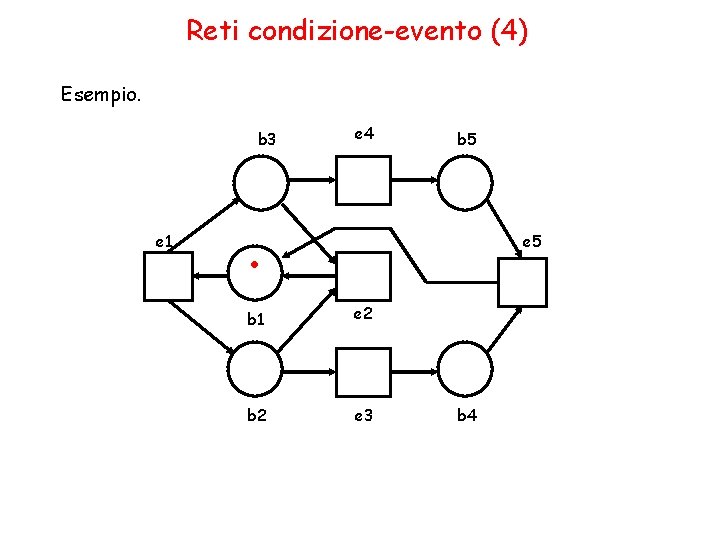
Reti condizione-evento (4) Esempio. b 3 e 1 e 4 b 5 . e 5 b 1 e 2 b 2 e 3 b 4

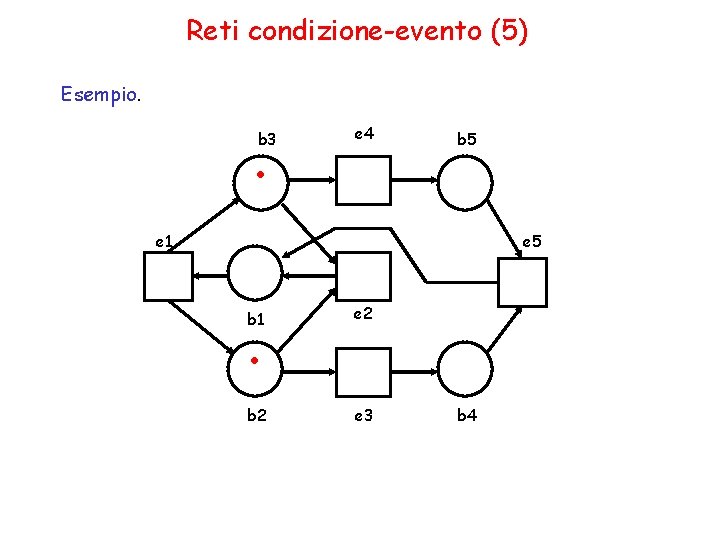
Reti condizione-evento (5) Esempio. . b 3 e 4 b 5 e 1 e 5 b 1 . e 2 b 2 e 3 b 4

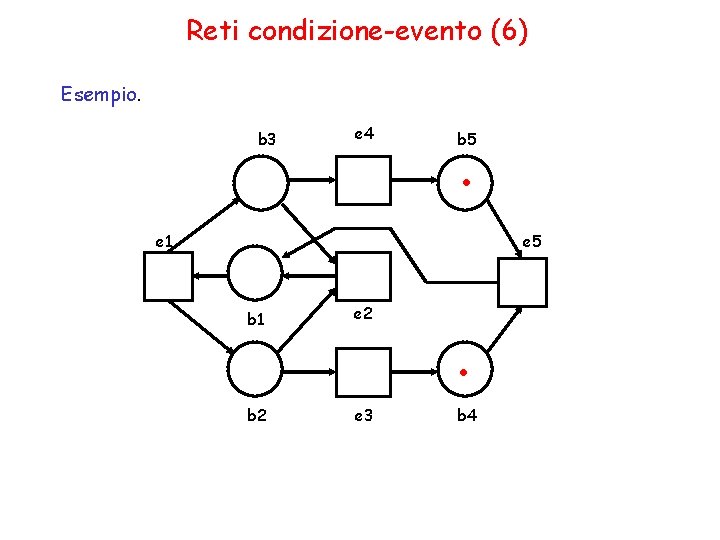
Reti condizione-evento (6) Esempio. b 3 e 4 . b 5 e 1 e 5 b 1 e 2 . b 2 e 3 b 4

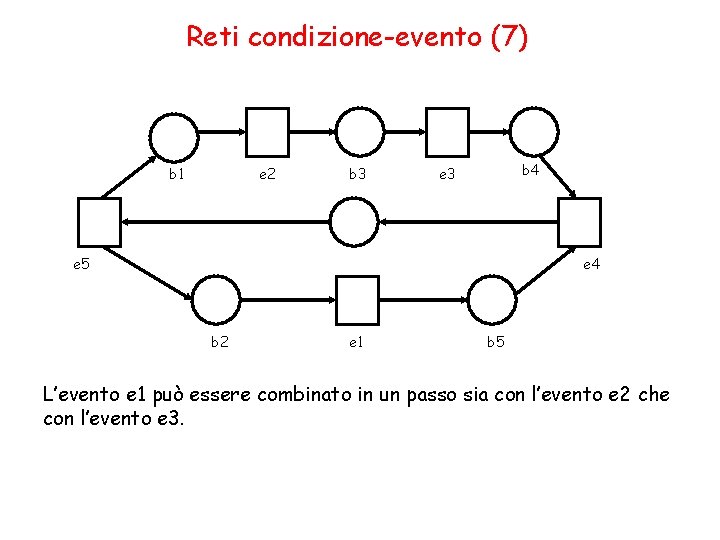
Reti condizione-evento (7) b 1 e 2 b 3 b 4 e 3 e 5 e 4 b 2 e 1 b 5 L’evento e 1 può essere combinato in un passo sia con l’evento e 2 che con l’evento e 3.

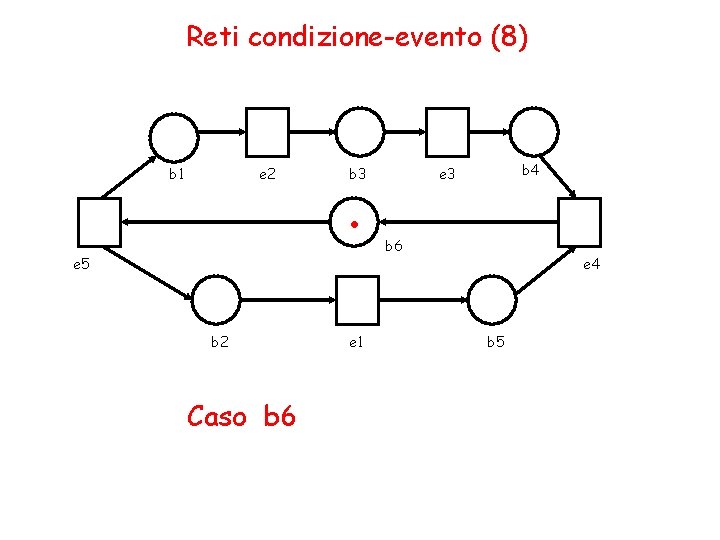
Reti condizione-evento (8) b 1 e 2 . b 3 e 5 b 2 Caso b 6 e 1 b 4 e 3 b 6 e 4 b 5

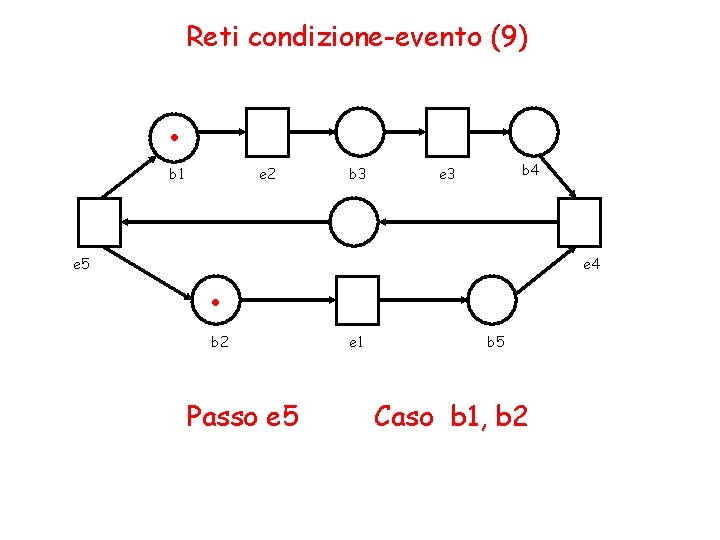
Reti condizione-evento (9) . b 1 e 5 e 2 b 3 b 4 e 3 . b 2 Passo e 5 e 4 e 1 b 5 Caso b 1, b 2

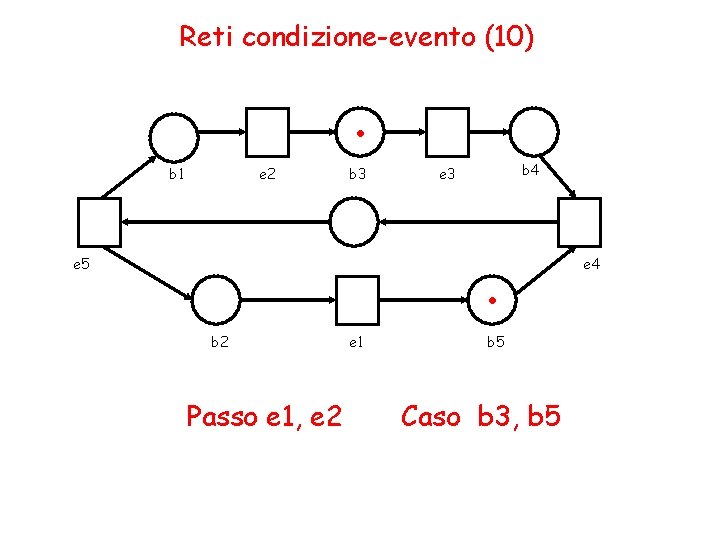
Reti condizione-evento (10) . b 1 e 2 b 3 b 4 e 3 . e 5 b 2 Passo e 1, e 2 e 1 b 5 Caso b 3, b 5 e 4

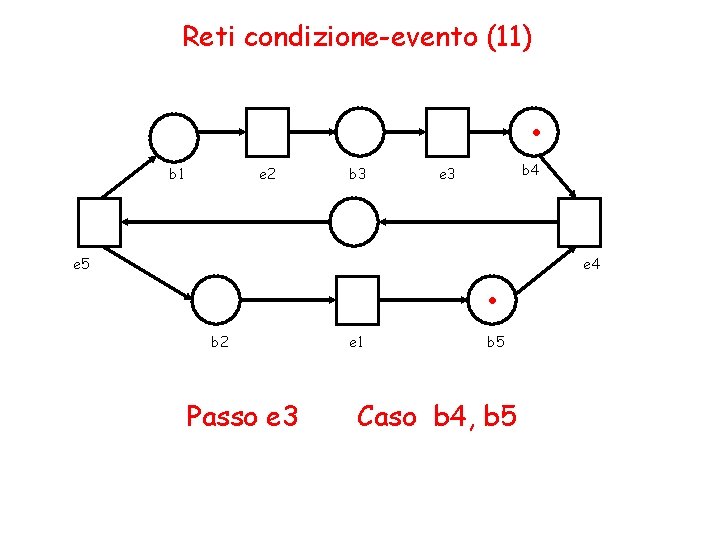
Reti condizione-evento (11) . b 1 e 2 b 3 b 4 e 3 . e 5 b 2 Passo e 3 e 1 b 5 Caso b 4, b 5 e 4

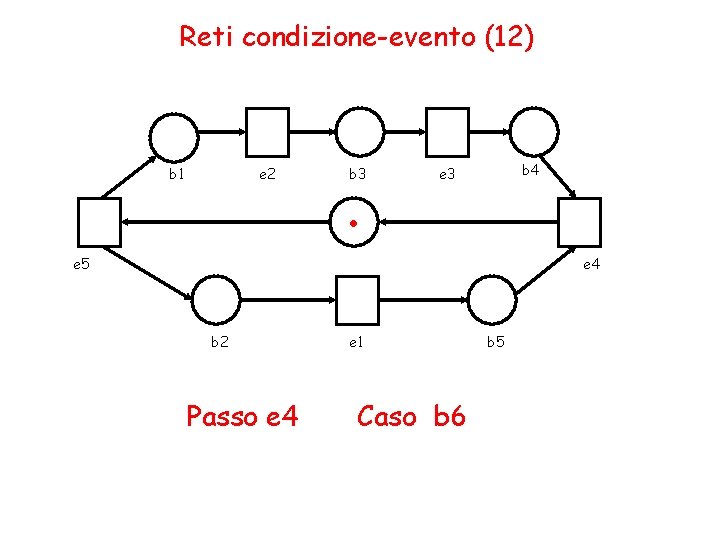
Reti condizione-evento (12) b 1 e 2 . b 3 b 4 e 3 e 5 e 4 b 2 Passo e 4 e 1 Caso b 6 b 5

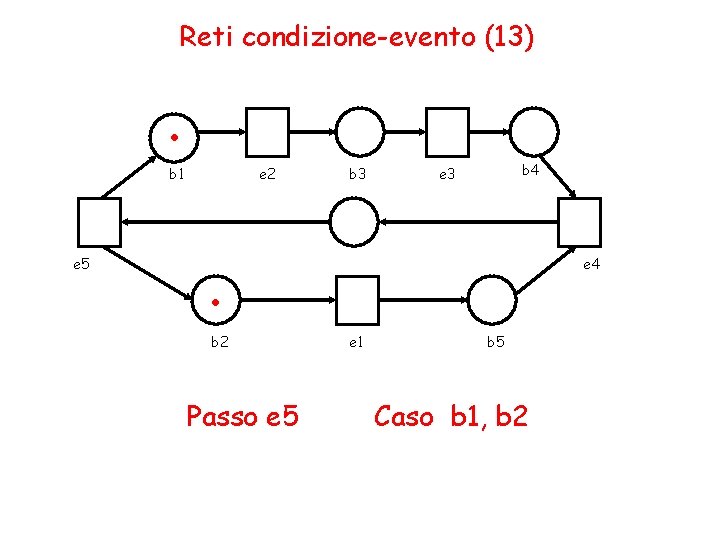
Reti condizione-evento (13) . b 1 e 5 e 2 b 3 b 4 e 3 . b 2 Passo e 5 e 4 e 1 b 5 Caso b 1, b 2

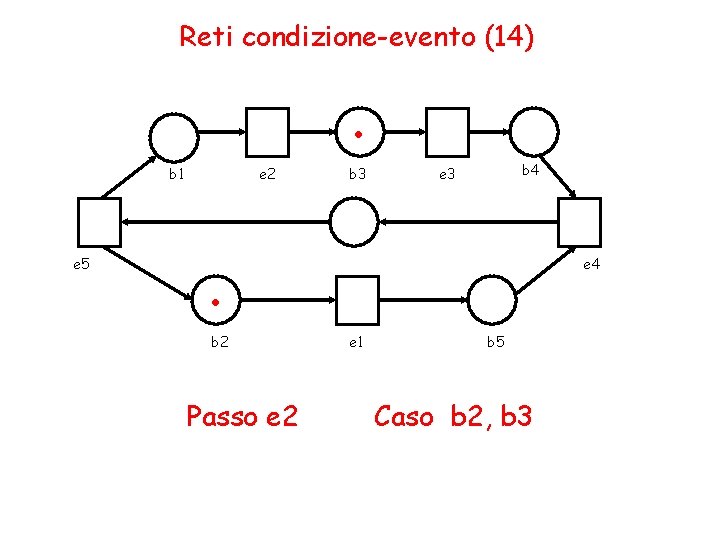
Reti condizione-evento (14) . b 1 e 5 e 2 b 3 b 4 e 3 . b 2 Passo e 2 e 4 e 1 b 5 Caso b 2, b 3

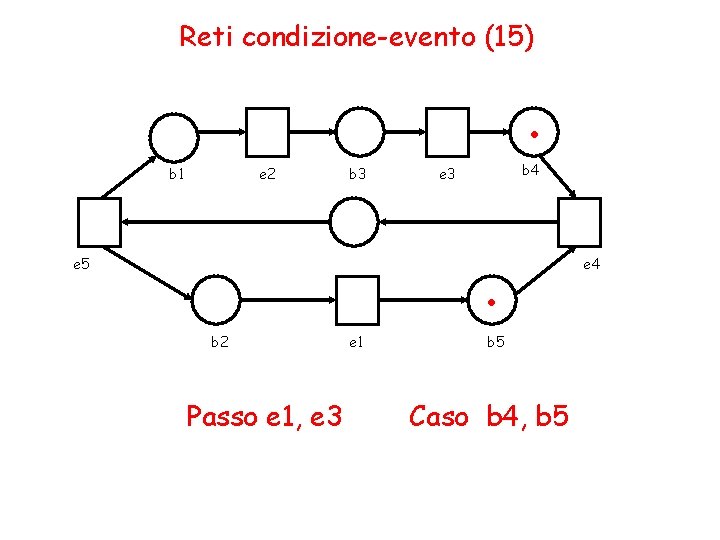
Reti condizione-evento (15) . b 1 e 2 b 3 b 4 e 3 . e 5 b 2 Passo e 1, e 3 e 1 b 5 Caso b 4, b 5 e 4

Reti condizione-evento (16) Un passo finito può essere realizzato con l’occorrenza dei suoi eventi in un ordine arbitrario. Lemma. Sia N una rete, c e c’ casi di N e G = {e 1, …, en} un passo finito da c a c’. Se (e 1, …, en) è un ordinamento arbitrario degli elementi di G allora ci sono casi c 0, …, cn tali che c = c 0, c’ = cn e ci-1 [ei> ci, (i = 1, …, n).

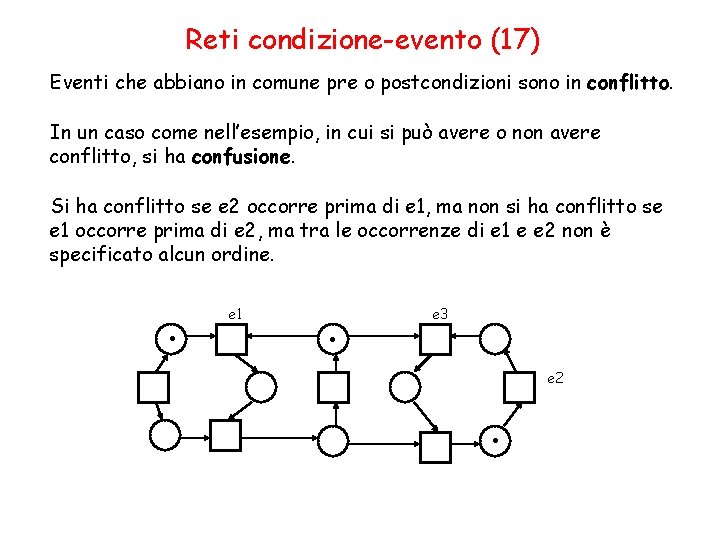
Reti condizione-evento (17) Eventi che abbiano in comune pre o postcondizioni sono in conflitto. In un caso come nell’esempio, in cui si può avere o non avere conflitto, si ha confusione. Si ha conflitto se e 2 occorre prima di e 1, ma non si ha conflitto se e 1 occorre prima di e 2, ma tra le occorrenze di e 1 e e 2 non è specificato alcun ordine. . e 1 . e 3 e 2 .

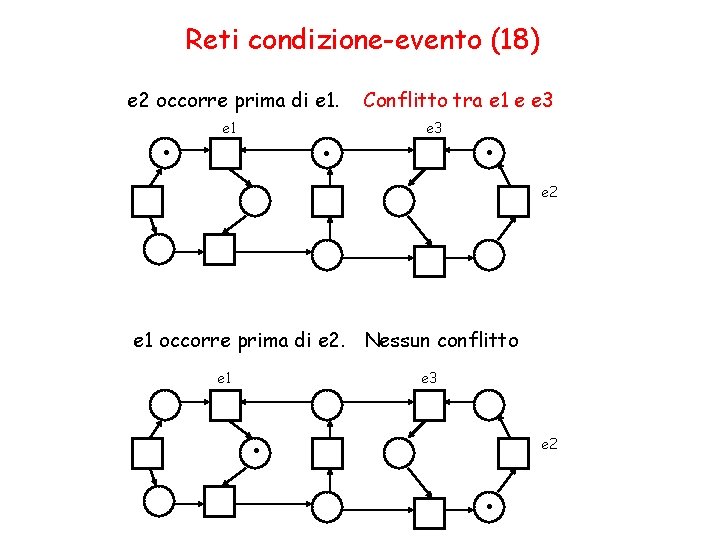
Reti condizione-evento (18) e 2 occorre prima di e 1. . . e 1 Conflitto tra e 1 e e 3 . e 2 e 1 occorre prima di e 2. Nessun conflitto e 1 e 3 . e 2 .

Sistemi condizione-evento (1) Un sistema condizione-evento consiste di una rete (B, E, F) e di un insieme di casi C con le proprietà seguenti: - Se un passo G E è possibile in un caso c C allora G porta a un caso in C - Se un caso c C risulta da un passo G E allora anche la configurazione di partenza è un caso di C - Tutti i casi di C possono essere trovati ragionando in avanti o all’indietro - C è tale che i) per ogni evento e E c’è un caso in C in cui e ha una concessione, ii) ogni condizione b B appartiene ad almeno un caso di C, ma non a tutti (cosí si escludono condizioni isolate e self-loop). Si vogliono escludere anche eventi isolati perché si vuole che gli eventi siano osservabili. Inoltre si chiede che due condizioni non abbiano lo stesso preset e postset (non sarebbero distinguibili). Analogamente per gli eventi.

Sistemi condizione-evento (2) Una quadrupla = (B, E, F, C) è un sistema condizione-evento (sistema C/E) se e solo se: 1. (B, E, F) è una rete semplice senza elementi isolati. 2. C (B) è una classe di equivalenza della relazione di raggiungibilità RS = (r r -1)*, dove r (B) è data da c 1 r c 2 $G E c 1 [G> c 2. C è la classe dei casi di . 3. Per ogni e E esiste c C tale che e ha una concessione in C. La classe dei casi di un sistema C/E S è completamente determinato da un elemento arbitrario della classe.

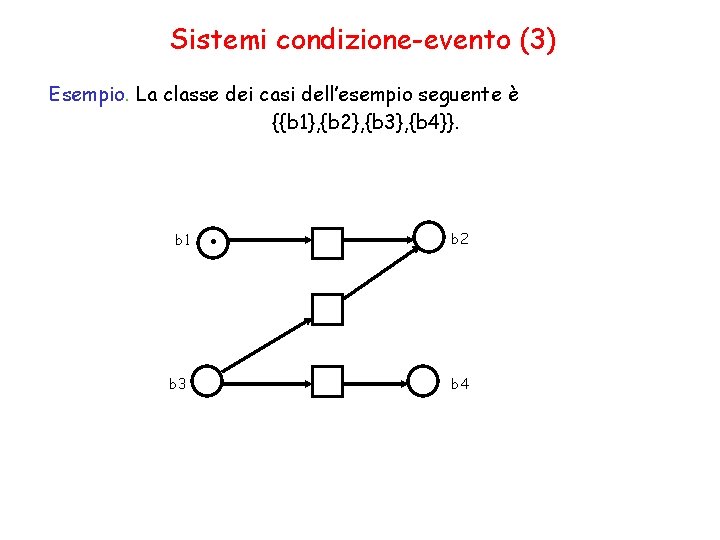
Sistemi condizione-evento (3) Esempio. La classe dei casi dell’esempio seguente è {{b 1}, {b 2}, {b 3}, {b 4}}. b 1 b 3 . b 2 b 4

Sistemi condizione-evento (4) Lemma. Sia un sistema C/E. 1. B e E e F sono differenti da . 2. Per c C , c’ B , G E c [G > c’ C c’[G > c c’ C. 3. Per ogni b B , c, c’ C con b c and b c’. 4. S è puro.

Sistemi ciclici e vivi (1) Un sistema C/E è ciclico se e solo se per ogni c 1, c 2 C c 1 r * c 2. Proposizione. Sia un sistema C/E ciclico e sia c C . Allora C = {c’ | c r * c’}. Un sistema C/E è vivo se e solo se per ogni c C e ogni e E $ c’ C tale che c r * c’ e e è c’-abilitato. Proposizione. Ogni sistema C/E ciclico è vivo.

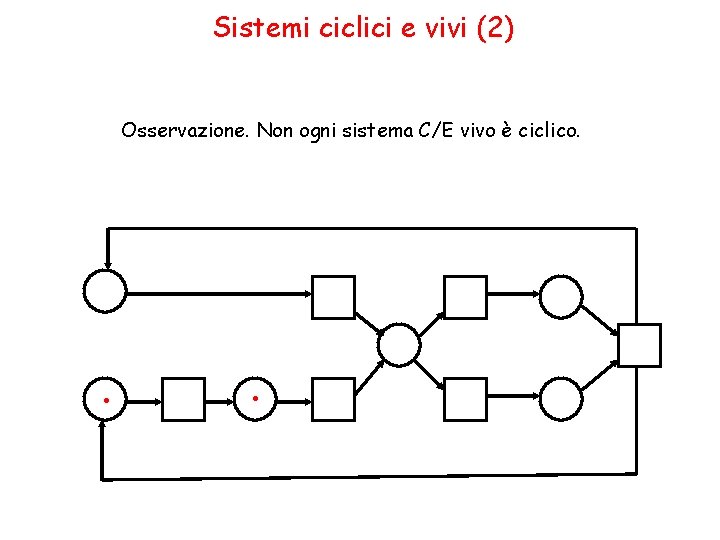
Sistemi ciclici e vivi (2) Osservazione. Non ogni sistema C/E vivo è ciclico. . .

Equivalenza di sistemi (1) Siano e ’ due sistemi C/E. 1. Date biiezioni g: C C ’, e: E E ’, e ’ sono (g, e)-equivalenti se solo se per tutti i casi c 1, c 2 C e tutti gli insiemi di eventi 2. G E c 1 [G> c 2 g(c 1) [e(G)> g(c 2), dove e(G) = {e(e) | e G}. e ’ sono equivalenti se solo se sono (g, e)-equivalenti per qualche coppia di biiezioni (g, e). e ’ sono isomorfi se e solo se le reti (B , E , F ) e (B ’, E ’, F ’) sono b-isomorfe per qualche biiezione b e se 3. c C {b(b)|b c} C ’. 2. Se e ’ sono equivalenti scriviamo ~ ’. Proposizione. La relazione ~ è una relazione di equivalenza.

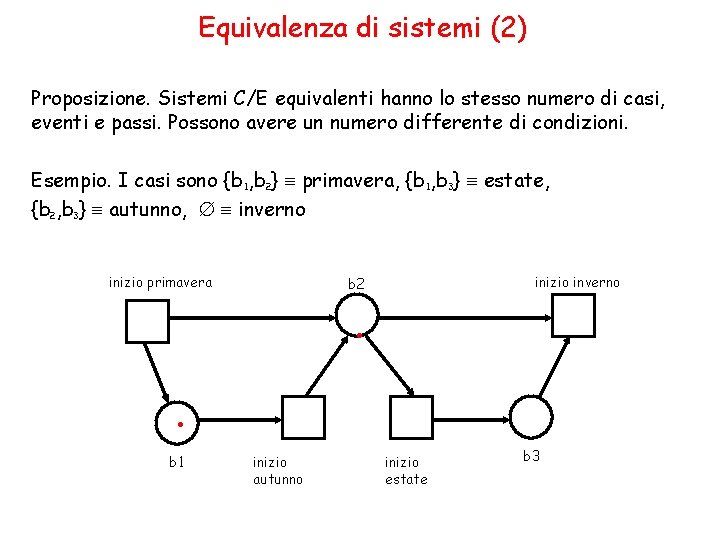
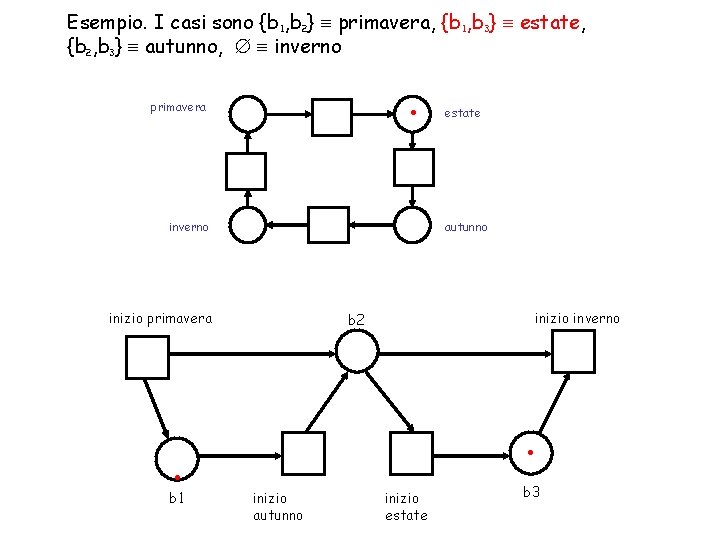
Equivalenza di sistemi (2) Proposizione. Sistemi C/E equivalenti hanno lo stesso numero di casi, eventi e passi. Possono avere un numero differente di condizioni. Esempio. I casi sono {b 1, b 2} primavera, {b 1, b 3} estate, {b 2, b 3} autunno, inverno inizio primavera inizio inverno b 2 . . b 1 inizio autunno inizio estate b 3

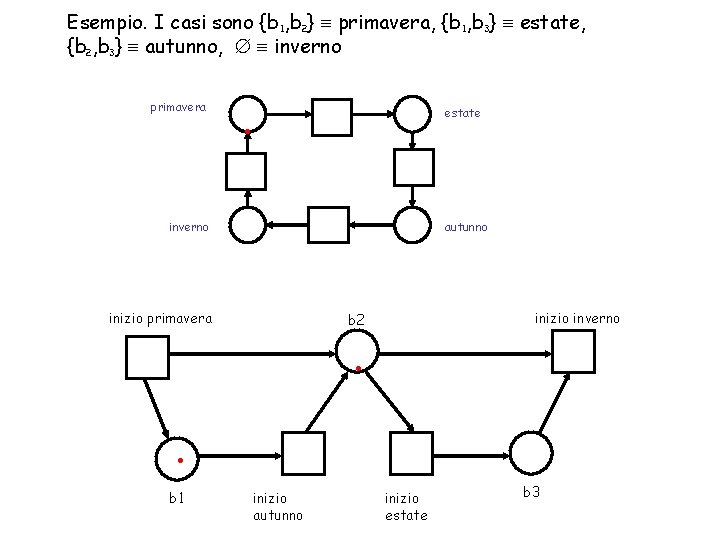
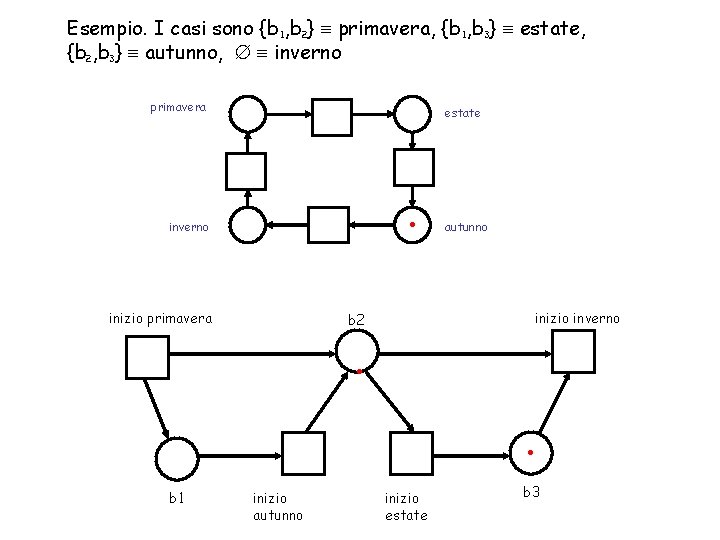
Esempio. I casi sono {b 1, b 2} primavera, {b 1, b 3} estate, {b 2, b 3} autunno, inverno primavera . estate inverno autunno inizio primavera inizio inverno b 2 . . b 1 inizio autunno inizio estate b 3

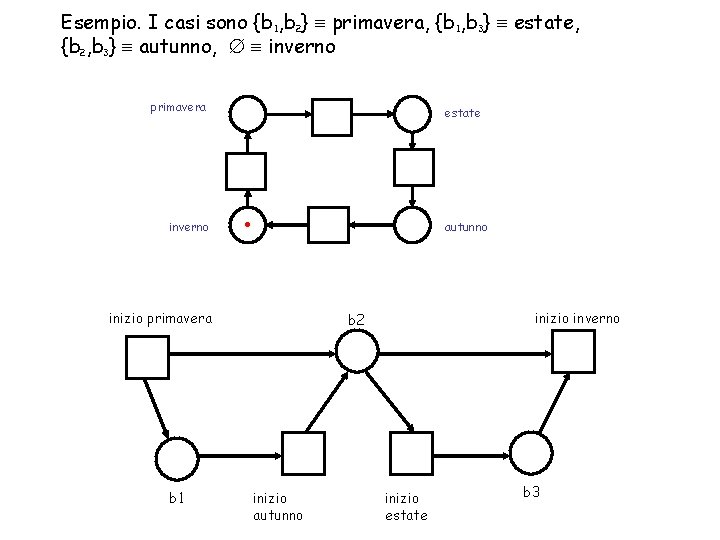
Esempio. I casi sono {b 1, b 2} primavera, {b 1, b 3} estate, {b 2, b 3} autunno, inverno . primavera inverno autunno inizio primavera . b 1 estate inizio inverno b 2 . inizio autunno inizio estate b 3

Esempio. I casi sono {b 1, b 2} primavera, {b 1, b 3} estate, {b 2, b 3} autunno, inverno primavera estate . inverno inizio primavera autunno inizio inverno b 2 . . b 1 inizio autunno inizio estate b 3

Esempio. I casi sono {b 1, b 2} primavera, {b 1, b 3} estate, {b 2, b 3} autunno, inverno primavera inverno estate . autunno inizio primavera b 1 inizio inverno b 2 inizio autunno inizio estate b 3

Equivalenza di sistemi (3) Proposizione. Siano e ’ due sistemi C/E equivalenti. 1. è ciclico se solo se ’ è ciclico. 2. è vivo se solo se ’ è vivo. Lemma. Siano e ’ sistemi C/E tali che per ogni c C C ’ |c| = 1. e ’ sono equivalenti se e solo se sono isomorfi.

Sistemi senza contatti (1) Un sistema C/E può essere trasformato in uno equivalente senza contatti. Contatto: in un caso c, . . e c e e. c . Sia un sistema C/E e siano b, b’ elementi di B . 1. b’ è il complemento di b se e solo se. b = b’. and b. =. b’. 2. è completo se ciascuna condizione b B ha un complemento 3. b’ B .

Sistemi senza contatti (2) Lemma. Sia un sistema C/E e sia b 1. B . b ha al piú un complemento b^. Se b ha un complemento b^, allora 2. b^ ha un complemento b^^ e b^^ = b. 3. Per ogni c C b c oppure b^ Se è completo allora 4. Per ogni e E |. e | = |e. |. 5. Per ogni c C | c | = 1/2 | B |. c.

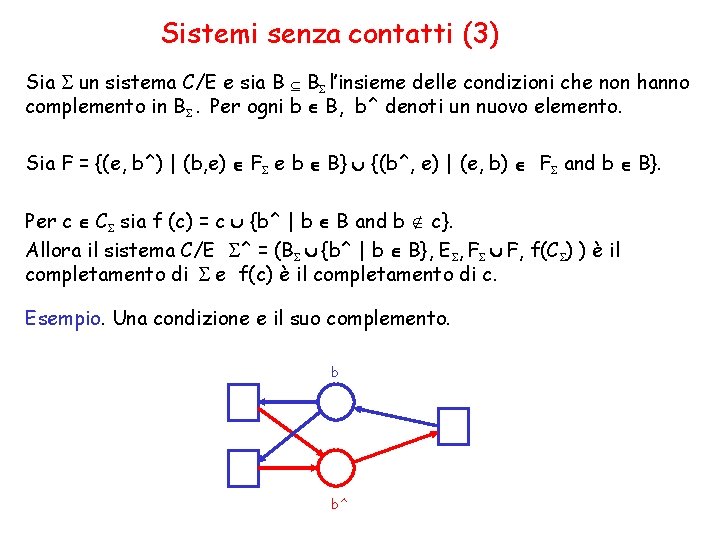
Sistemi senza contatti (3) Sia un sistema C/E e sia B B l’insieme delle condizioni che non hanno complemento in B . Per ogni b B, b^ denoti un nuovo elemento. Sia F = {(e, b^) | (b, e) F e b B} {(b^, e) | (e, b) F and b B}. Per c C sia f (c) = c {b^ | b B and b c}. Allora il sistema C/E ^ = (B {b^ | b B}, E , F F, f(C ) ) è il completamento di e f(c) è il completamento di c. Esempio. Una condizione e il suo complemento. b b^

Sistemi senza contatti (4) Proposizione. Sia un sistema C/E e c C . Vale 1. ^^ = ^ 2. Per ogni b 3. c = f(c) B . B , c C b f(c) b^ f(c)

Sistemi senza contatti (4) Lemma. La funzione f : C C ^ come definita sopra è biiettiva. Notazione. Denotiamo con -e ed e- preset e postset di e in ^. Proposizione. Sia un sistema C/E, sia G E e B l’insieme delle condizioni che non hanno complemento in B. Vale: 1. 2. 2. 3. -G =. G {b^ | b B and b G. }, G- = G. {b^ | b B and b . G} . G = -G B , G. = G - B.

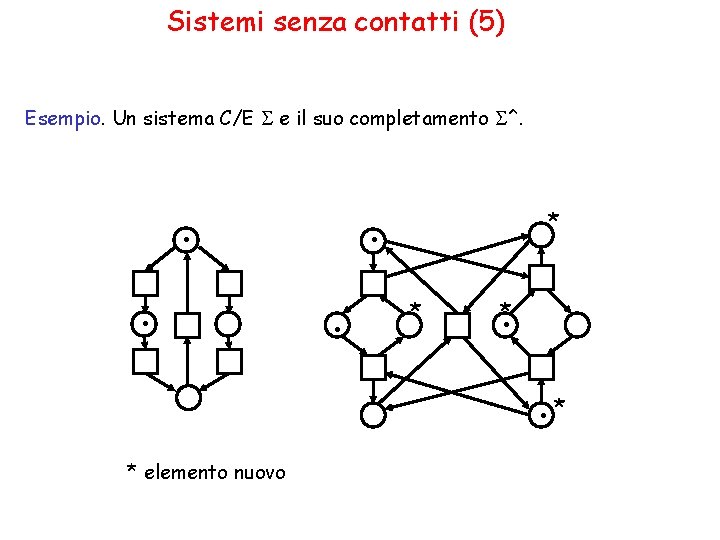
Sistemi senza contatti (5) Esempio. Un sistema C/E e il suo completamento ^. . . * * elemento nuovo

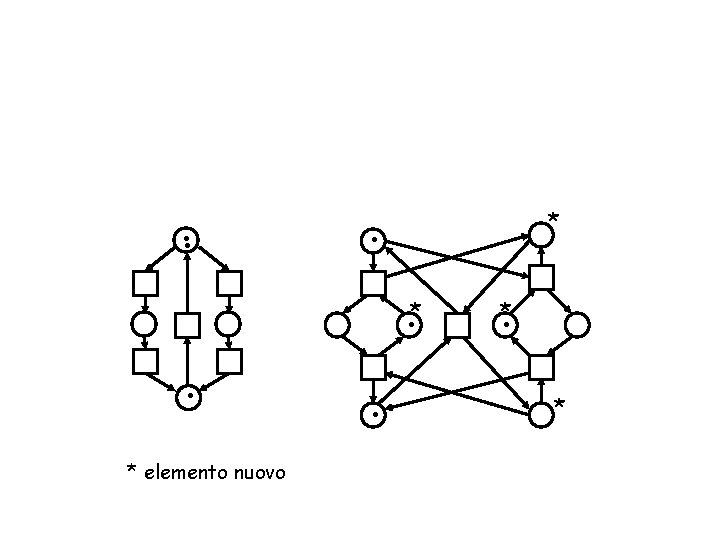
. . * . *. * elemento nuovo . . * *

Sistemi senza contatti (6) Teorema. Se ^ è il complemento di un sistema C/E , allora ^ è equivalente a . Dimostrazione. Bisogna dimostrare che per ogni c 1, c 2 C , per ogni G R c 1 [G> c 2 f(c 1) [G> f(c 2). Un sistema C/E è senza contatti se per ogni e 1. . e c e. B c 2. e. c . e B c . E e ogni c Teorema. 1. Ogni sistema C/E completo è senza contatti. 2. Per ogni sistema C/E ce ne è uno equivalente senza contatti. 3. Se è senza contatti allora per ogni e E . e diverso da e. diverso da . C

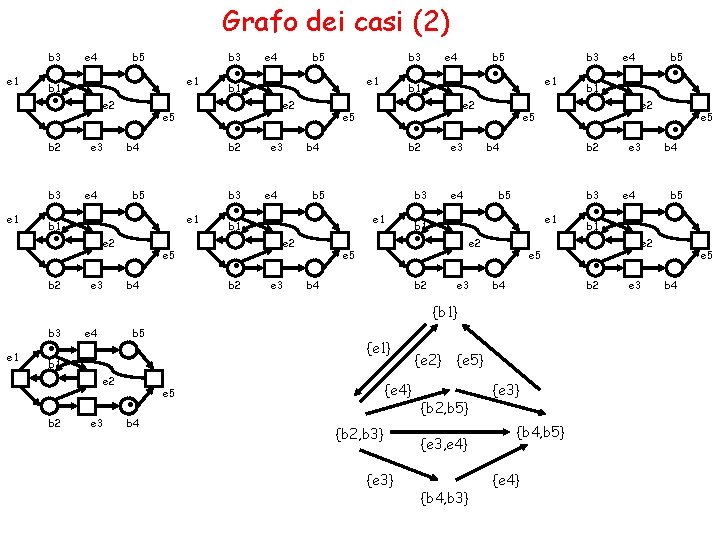
Grafo dei casi (1) Il grafo dei casi ha come nodi i casi e come archi i passi del sistema C/E. Sia un sistema C/E, S l’insieme di tutti i passi di , P = {(c 1, G, c 2) C S C | c 1 [G> c 2}. � Il grafo F = (C , P) è chiamato grafo dei casi di .

Grafo dei casi (2) b 3 e 1 . e 2 e 3 e 5 b 4 e 4 . b 3 e 5 b 4 b 5 b 3 e 1 e 2 e 3 b 2 . e 5 b 5 e 2 e 3 b 3 e 1 b 4 e 2 b 5 e 1 e 2 b 2 e 3 e 4 b 5 e 2 e 3 . b 4 {e 1} {e 4} e 5 {b 2, b 3} {e 2} e 5 b 4 {e 3, e 4} {b 4, b 3} {e 3} {b 4, b 5} {e 4} e 3 e 5 b 4 e 4 b 5 b 1 b 2 {e 5} {b 2, b 5} . . b 3 . . b 5 b 1 b 2 b 1 e 5 e 4 e 5 b 4 e 4 . e 1 b 3 e 2 b 1 b 5 b 1 b 4 e 4 {b 1} b 1 b 2 . . b 3 e 1 e 4 b 1 b 2 b 5 e 2 . . b 3 b 1 b 2 e 1 b 5 b 1 b 2 e 1 e 4 e 2 e 3 e 5 b 4

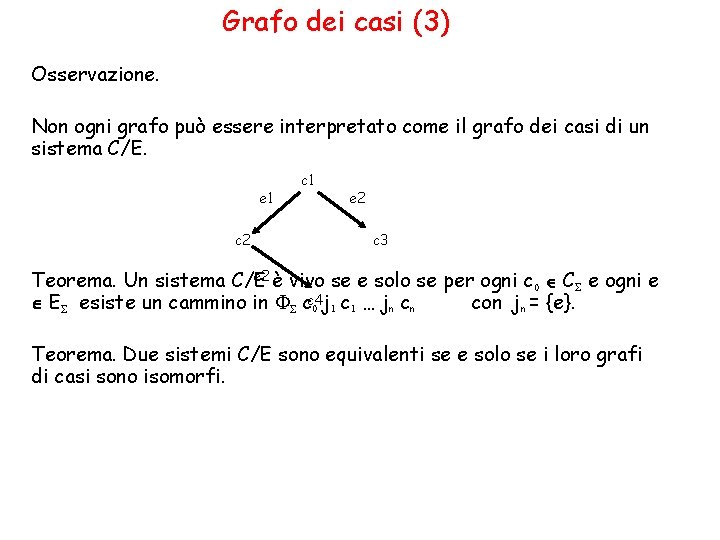
Grafo dei casi (3) Osservazione. Non ogni grafo può essere interpretato come il grafo dei casi di un sistema C/E. e 1 c 2 c 1 e 2 c 3 e 2 è vivo se e solo se per ogni c C e ogni e Teorema. Un sistema C/E 0 E esiste un cammino in F cc 4 con jn = {e}. 0 j 1 c 1 … jn c n Teorema. Due sistemi C/E sono equivalenti se e solo se i loro grafi di casi sono isomorfi.

Grafo dei casi (4) Teorema. Un sistema C/E è ciclico se e solo se il suo grafo dei casi è fortemente connesso. Teorema. Sia un sistema C/E, siano c 1 , c 2 , c 3 C e G 1 , G 2 E . 1. Se c 1 G 1 c 2 G 2 c 3 è un cammino in F allora G 1 G 2 = . 2. Sia G 1 G 2 = . Allora se c 1 ( G 1 G 2) c 3 è un arco in F allora esiste c C tale che c 1 G 1 c G 2 c 3 è un cammino in F .

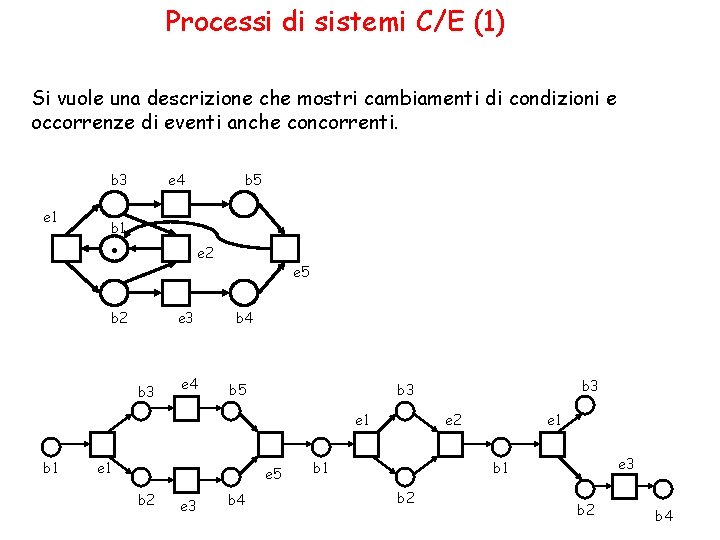
Processi di sistemi C/E (1) Si vuole una descrizione che mostri cambiamenti di condizioni e occorrenze di eventi anche concorrenti. b 3 e 1 e 4 . b 5 b 1 e 2 b 2 e 3 b 3 e 4 e 5 b 4 b 5 e 1 b 1 e 5 b 2 e 3 b 4 b 3 e 2 b 1 e 3 b 1 b 2 b 4

Processi di sistemi C/E (2) Un T-elemento rappresenta l’occorrenza dell’evento denotato dalla sua etichettatura. T-elementi distinti con la stessa etichettatura denotano occorrenze differenti del medesimo evento. Un S-elemento s mostra con la sua iscrizione b che b è stata soddisfatta dall’occorrenza di. s e ha cessato di valere con l’occorrenza di s. . I conflitti sono stati risolti e tutti gli S-elementi non hanno diramazioni.

Processi di sistemi C/E (3) Una relazione binaria r A A su un insieme A è una relazione di similarità se e solo se 1. Per ogni a A: a r a (r è riflessiva) 2. Per ogni a, b A: a r b = b r a (r è simmetrica) Un sottoinsieme B A è una regione di una relazione di similarità r se e solo se 1. Per ogni a, b B: a r b (r è full su B) 2. Per ogni a A: a B b B: not (a r b) 3. (B è un sottoinsieme massimale su cui r è full) Proposizione. Sia A un insieme e r A A una relazione di similarità. 1. Ogni elemento di A appartiene ad almeno una regione di r. 2. Regioni di un insieme non vuoto A sono non vuote e nessuna 3. regione è un sottoinsieme proprio di un’altra regione. 3. Se r è una relazione di equivalenza allora le regioni di r sono 4. esattamente le classi di equivalenza di r.

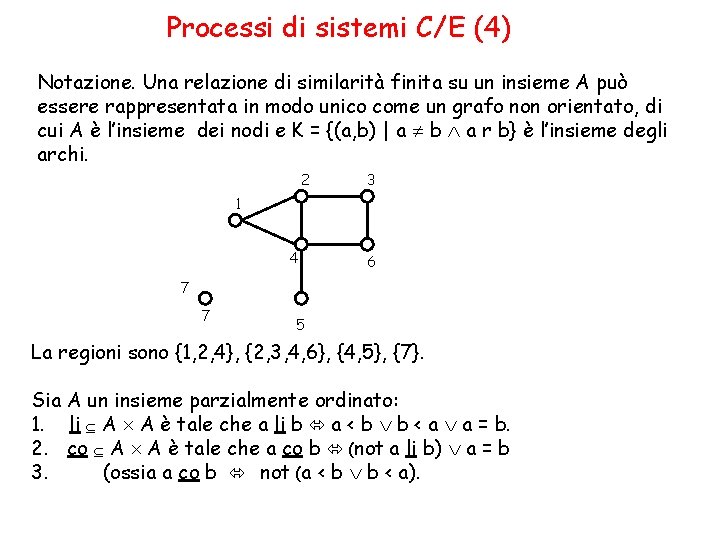
Processi di sistemi C/E (4) Notazione. Una relazione di similarità finita su un insieme A può essere rappresentata in modo unico come un grafo non orientato, di cui A è l’insieme dei nodi e K = {(a, b) | a b a r b} è l’insieme degli archi. 2 3 1 4 6 7 7 5 La regioni sono {1, 2, 4}, {2, 3, 4, 6}, {4, 5}, {7}. Sia A un insieme parzialmente ordinato: 1. li A A è tale che a li b a < b b < a a = b. 2. co A A è tale che a co b (not a li b) a = b 3. (ossia a co b not (a < b b < a).

Processi di sistemi C/E (5) Sia A un insieme parzialmente ordinato e siano a, b A : 1. a li b a co b. 2. a li b a co b a = b. Teorema. Per un qualsiasi insieme parzialmente ordinato A, li e co sono relazioni di similarità. Esempio. 1 2 3 5 4 6 7 La regioni di li sono {1, 2, 5, 6, 7}, {1, 2, 3}, {4, 6, 7}. Le regioni di co sono {3, 7}, {3, 6}, {3, 4, 5}, {1, 4}, {2, 4}.

Processi di sistemi C/E (6) Sia A un insieme parzialmente ordinato e sia B A: 1. B è una linea se e solo se B è una regione di li. 2. B è un taglio se e solo se B è una regione di co. Sia A un insieme parzialmente ordinato e siano B, C A. 1. A è limitato (bounded) se e solo se esiste n N tale che per ogni linea L di A |L| n. 2. B precede C (scritto B C) se e solo se per ogni b B e per ogni c C b < c or b co c 3. ( scriviamo B < C per B C and B C) 3. B- = {a A | {a} B}, B+ = {a A | B {a}}. 4. o. B = {b B | per ogni b’ B, b co b’ b < b’}, Bo = {b B | per ogni b’ B, b co b’ < b}. o. B è l’insieme degli elementi minimali di B e Bo è l’insieme degli elementi massimali di B.

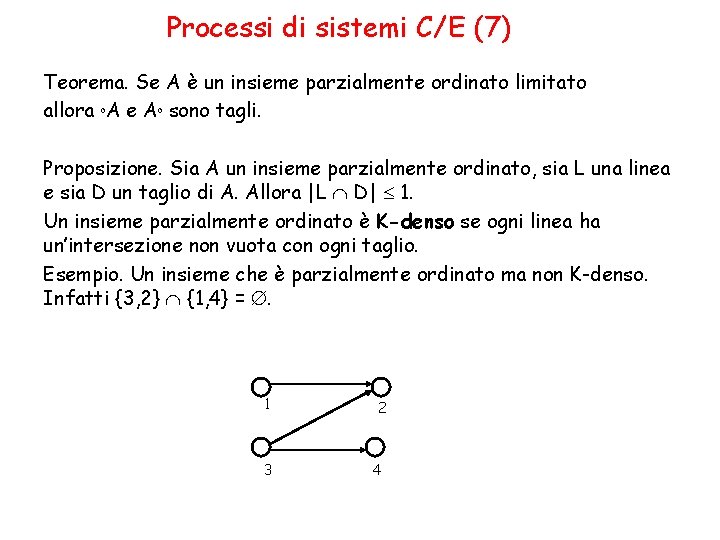
Processi di sistemi C/E (7) Teorema. Se A è un insieme parzialmente ordinato limitato allora o. A e Ao sono tagli. Proposizione. Sia A un insieme parzialmente ordinato, sia L una linea e sia D un taglio di A. Allora |L D| 1. Un insieme parzialmente ordinato è K-denso se ogni linea ha un’intersezione non vuota con ogni taglio. Esempio. Un insieme che è parzialmente ordinato ma non K-denso. Infatti {3, 2} {1, 4} = . 1 3 2 4

Processi di sistemi C/E (8) Una rete K = (SK , TK, FK) è una rete di occorrenze se e solo se: 1. Per ogni a, b K: a (FK+) b b (FK+) a (K è senza cicli) 2. Per ogni s SK : |. s| 1 |s. | 1 (gli S-elementi non hanno diramazioni) Proposizione. Sia K una rete di occorrenze. La relazione <, definita da a < b a (FK+) b, per ogni a, b K, è un ordine parziale su K.

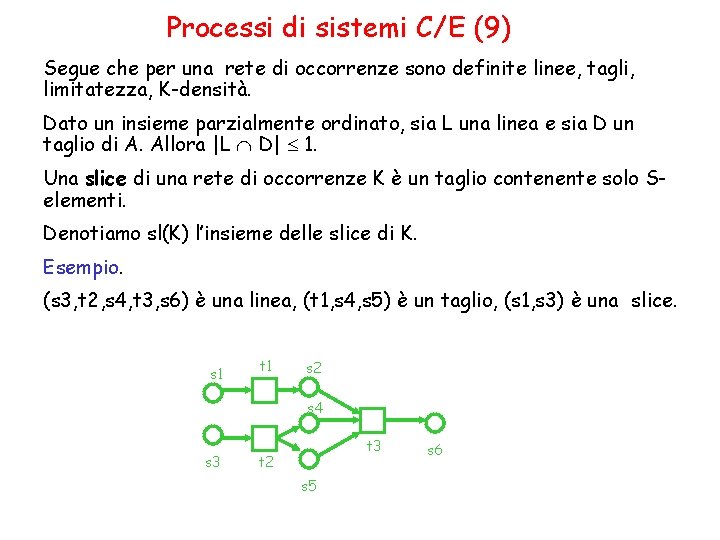
Processi di sistemi C/E (9) Segue che per una rete di occorrenze sono definite linee, tagli, limitatezza, K-densità. Dato un insieme parzialmente ordinato, sia L una linea e sia D un taglio di A. Allora |L D| 1. Una slice di una rete di occorrenze K è un taglio contenente solo Selementi. Denotiamo sl(K) l’insieme delle slice di K. Esempio. (s 3, t 2, s 4, t 3, s 6) è una linea, (t 1, s 4, s 5) è un taglio, (s 1, s 3) è una slice. s 1 t 1 s 2 s 4 s 3 t 2 s 5 s 6

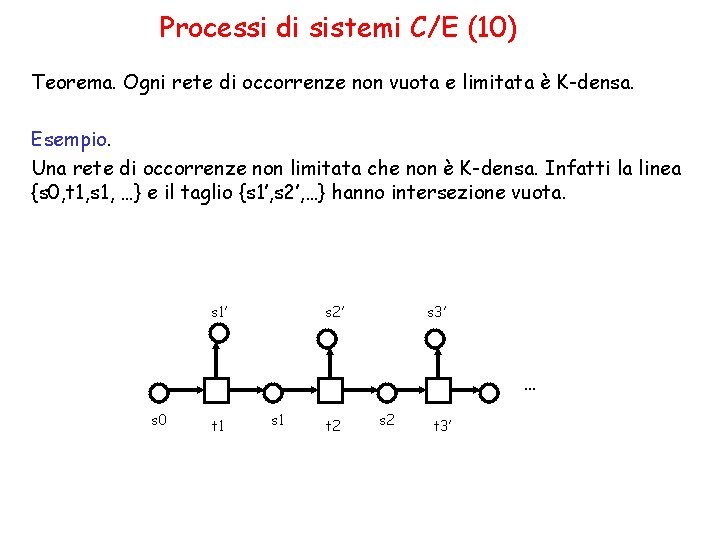
Processi di sistemi C/E (10) Teorema. Ogni rete di occorrenze non vuota e limitata è K-densa. Esempio. Una rete di occorrenze non limitata che non è K-densa. Infatti la linea {s 0, t 1, s 1, …} e il taglio {s 1’, s 2’, …} hanno intersezione vuota. s 1’ s 2’ s 3’ … s 0 t 1 s 1 t 2 s 2 t 3’

Processi di sistemi C/E (11) Descriviamo i processi come funzioni da reti di occorrenze limitate a sistemi C/E senza contatti soddisfacenti due richieste: 1. Ogni slice corrisponde a in un caso 2. La corrispondenza di un T-elemento rispetta l’ambiente dell’evento. Sia K una rete di occorrenze limitata e un sistema C/E senza contatti. Una funzione p: K è un processo di se e solo se per ogni slice D di K e ogni t TK : 1. p|D è iniettiva e p(D) CS 2. p(. t) =. p(t) p(t. ) = p(t). Nelle rappresentazioni grafiche di processi p: K ogni elemento x di K è etichettato dalla sua immagine p(x). Ogni linea rappresenta una successione di elementi casualmente dipendenti (sottoprocesso sequenziale), un taglio è un’istantanea (snapshot) del processo. La K-densità garantisce che ogni sottoprocesso sequenziale è rappresentato in ogni snapshot.

Processi di sistemi C/E (12) Teorema. Per ogni processo p: K : 1. p(SK) BS p(TK) ES (il tipo degli elementi e’ preservato). 2. Per ogni x, y K, x FK y p(x) FS p(y) (p rispetta la relazione di flusso) 3. Per ogni x, y K, p(x) = p(y) x li y (eventi e condizioni non sono concorrenti con loro stessi). 4. Per ogni t TK , . t and t. (eventi hanno prerequisiti e conseguenze). 5. Per ogni taglio D di K p|D è iniettiva.

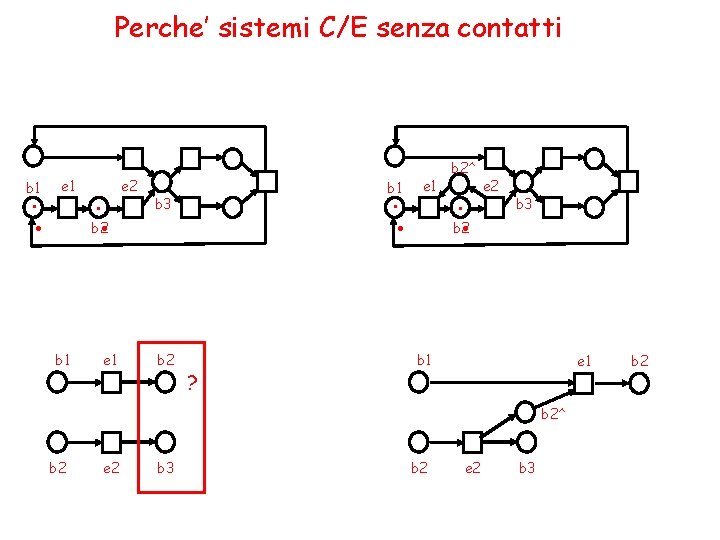
Perche’ sistemi C/E senza contatti . b 1 . e 1 . . e 2 . b 1 . b 3 b 2 b 1 e 1 b 2 ? e 1 b 2^ . . e 2 b 3 b 2 b 1 e 1 b 2^ b 2 e 2 b 3 b 2

Processi di sistemi C/E (13) Teorema. Sia p: K un processo, sia T TK tale che per ogni t 1, t 2 T, t 1 co t 2. Allora c 1, c 2 CS tali che c 1 [p(T)> c 2. Due processi p 1: K 1 , p 2: K 2 di un sistema C/E sono isomorfi se e solo se K 1 è b-isomorfo a K 2 e per ogni x K 1 p 1(x) = p 2(b(x)). Teorema. Siano 1 e 2 due sistemi C/E senza contatti e sia pi l’insieme dei processi di i (i=1, 2). Allora p 1 = p 2 1 = 2.

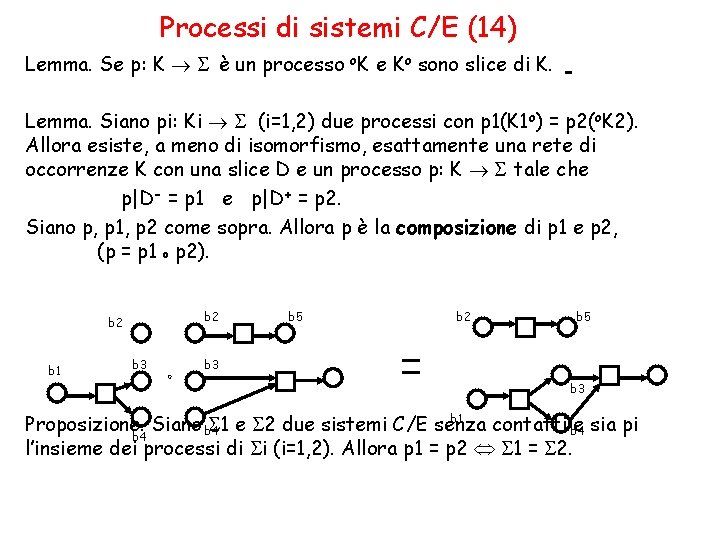
Processi di sistemi C/E (14) Lemma. Se p: K è un processo o. K e Ko sono slice di K. Lemma. Siano pi: Ki (i=1, 2) due processi con p 1(K 1 o) = p 2(o. K 2). Allora esiste, a meno di isomorfismo, esattamente una rete di occorrenze K con una slice D e un processo p: K tale che p|D- = p 1 e p|D+ = p 2. Siano p, p 1, p 2 come sopra. Allora p è la composizione di p 1 e p 2, (p = p 1 o p 2). b 2 b 1 b 3 o b 5 b 2 b 5 b 3 b 1 Proposizione. Siano b 4 1 e 2 due sistemi C/E senza contatti b 4 e sia pi b 4 l’insieme dei processi di i (i=1, 2). Allora p 1 = p 2 1 = 2.

Processi di sistemi C/E (15) Un processo è elementare se descrive un passo singolo. I processi sono decomponibili in un numero finito di processi elementari. Un processo p: K è elementare se solo se SK = o. K Ko. Proposizione. 1. p: K è un processo elementare se e solo se p(o. K) [p(TK) > p(Ko) è un passo di . 2. Se p: K è elementare allora per ogni t 1, t 2 TK t 1 co t 2.

Processi di sistemi C/E (16) Un processo è vuoto se e solo se TK = . Proposizione. 1. Ogni processo vuoto è elementare. 2. Se p’ è un processo vuoto ed è definito p o p’ (oppure p’ o p) allora p = p o p’ (oppure p = p’o p). Teorema. Se p: K è un processo, allora esiste un numero finito di processi elementari p 1, …, pn tali che p = p 1 o …o pn.

Processi e grafi dei casi (1) Processi elementari corrispondono ad archi in grafi dei casi. Piú cammini in un grafo dei casi possono corrispondere allo stesso processo. Lemma. Sia un sistema C/E senza contatti. Allora p: K è un processo elementare se e solo se c’è un arco = (c 1, G, c 2) in F tale che p(o. K) = c 1, p(Ko ) = c 2, p(TK) = G. Sia un sistema senza contatti. 1. Se v è un arco in F , allora v denota il processo corrispondente a v. v è il processo di v, v è l’arco di v. 2. Siano v 1, …, vn archi e sia w = v 1 … vn un cammino in F. Allora w = v 1 o … o vn è il processo di w e w è un cammino di w. v

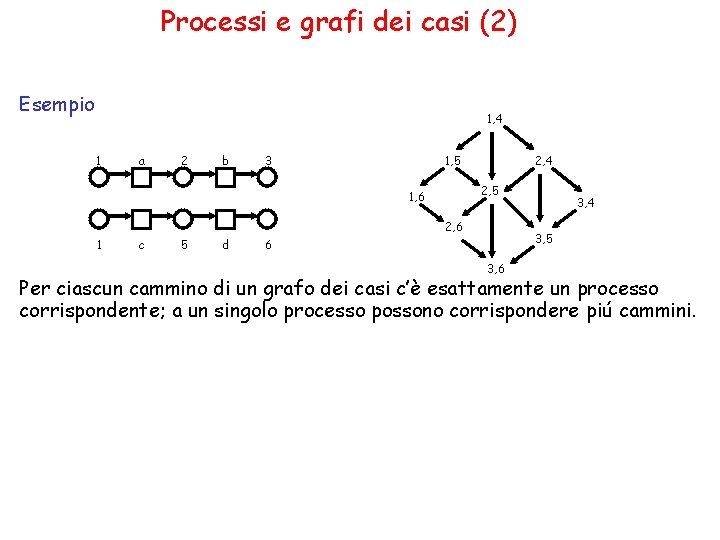
Processi e grafi dei casi (2) Esempio 1, 4 1 a 2 b 3 1, 5 2, 4 2, 5 1, 6 2, 6 1 c 5 d 3, 4 3, 5 6 3, 6 Per ciascun cammino di un grafo dei casi c’è esattamente un processo corrispondente; a un singolo processo possono corrispondere piú cammini.

Processi e grafi dei casi (3) Sia un sistema C/E, siano c 1, c 2, c 3 CS e G 1, G 2 ES. 1. Se u 1 = (c 1, G 1, c 2), u 2 = (c 1, G 2, c 3), v = (c 1, G 1 G 2, c 3) sono archi in F , il cammino u 1 u 2 è una decomposizione di v, v è una unificazione di u 1 u 2. 2. Dati cammini w, w’ è una permutazione di w se e solo se esistono cammini u 1, …, u 4 tali che w = u 1 u 2 u 3, w’ = u 1 u 4 u 3 e u 4 è una decomposizione o una unificazione di u 2. 3. Dati cammini w 1, …, wn in F , (w 1, …, wn) è una sequenza di permutazione se e solo se per ogni i = 1, …, n-1, wi+1 è una permutazione di wi.

Processi e grafi dei casi (4) Proposizione. Sia un sistema C/E senza contatti, siano c 1, c 2, c 3 C e siano G 1, G 2 E disgiunti e non vuoti. 1. Se v = c 1 (G 1 G 2) c 2 è un arco in F , allora esiste una decomposizione di v della forma c 1 G 1 c G 2 c 2, per un qualche c C . 2. Siano u 1 = c 1 G 1 c 3 e u 2 = c 3 G 2 c 2 archi in F e sia u 1 o u 2 : K . Allora per ogni t 1, t 2 TK: t 1 co t 2 se e solo se c 1 (G 1 G 2) c 2 è un arco in F .

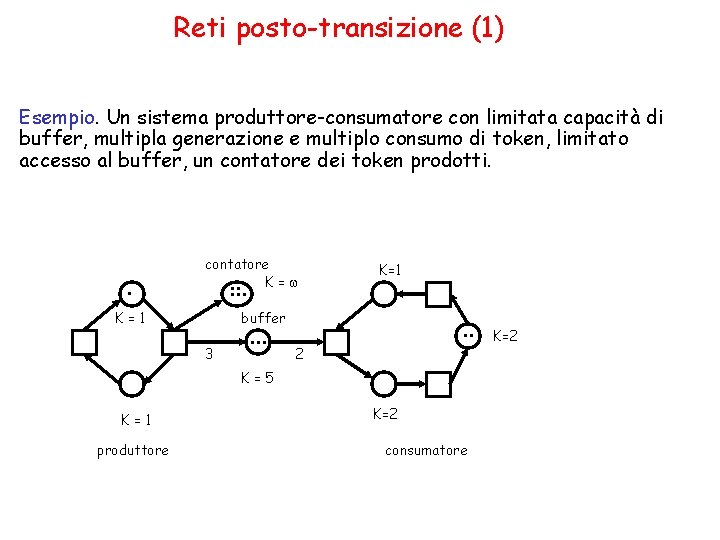
Reti posto-transizione (1) Esempio. Un sistema produttore-consumatore con limitata capacità di buffer, multipla generazione e multiplo consumo di token, limitato accesso al buffer, un contatore dei token prodotti. . contatore K=w . . . K=1 buffer 3 . . . 2 K=5 K=1 produttore K=2 consumatore K=2

Reti posto-transizione (2) Una sestupla N = (S, T, F, K, M, W) è una rete P/T se e solo se : 1. (S, T, F) è una rete finita, gli elementi di S sono i posti, gli elementi di T sono le transizioni. 2. K : S N {w} dà la capacità di ciascun posto. 3. W : F N {0} dà un peso a ciascun arco della rete. 4. M : S N ogni s S. { w} è la marcatura iniziale tale che M(s) K(s) per

Reti posto-transizione (3) Denotiamo le componenti di una rete P/T N con S N, TN, FN, KN, MN, WN. Sia N una rete P/T. 1. Una funzione M : SN N {w } è una marcatura di N se e solo se M(s) K(s). 2. Data una marcatura M, una transizione t TN è M-abilitata se e solo se per ogni s. t M(s) ≥ WN (s, t) e per ogni s t. M(s) + WN (t, s) KN (s). 3. Una transizione M-abilitata t TN può dare una marcatura successiva M’ di M che per ogni s è: M(s) - WN (s, t) se e solo se s . t t. M(s) + WN (t, s) se e solo se s t. . t M(s) - WN (s, t) + WN (t, s) se e solo se s . t t. M(s) altrimenti. Diciamo che t porta da M a M’ e scriviamo M[t> M’. 4. Sia [M > il piú piccolo insieme di marcature tale che M [M > e, se M 1 M e per qualche t TN M 1 [t> M 2 allora M 2 [M>.

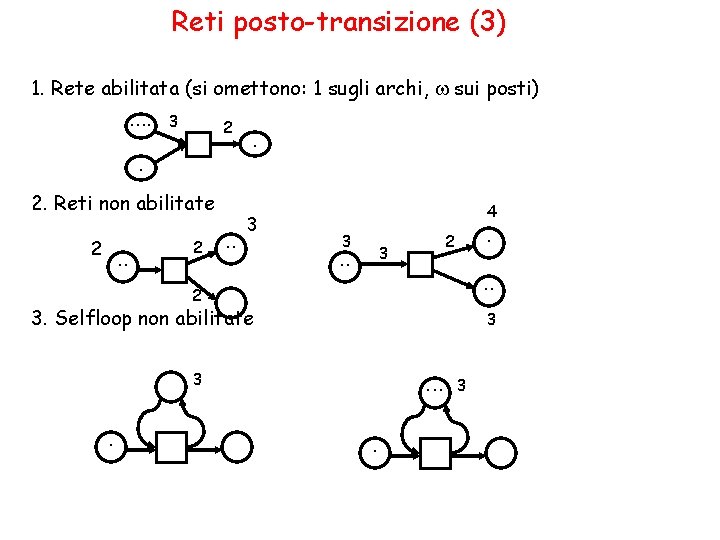
Reti posto-transizione (3) 1. Rete abilitata (si omettono: 1 sugli archi, w sui posti). . 3 2. Reti non abilitate 2 . . 3 4 3 3 . . 2 3. Selfloop non abilitate 3 3 . . . 3 .

Reti posto-transizione (4) Una marcatura di una rete P/T ha un contatto per una transizione t TN se t non è M-abilitata solo perché i posti in t non hanno la capacità sufficiente. o Una rete P/T N è senza contatti (contact-free) se e solo se per ogni M [MN> e per ogni t TN se s . t M(s) WN (s, t) allora s t. KN (s) - WN (t, s) M(s)

Reti posto-transizione (5) Costruzione della rete completata: Data una rete P/T N la corrispondente rete N’ è ottenuta aggiungendo nuovi posti e nuovi archi. Per ogni posto s di N aggiungiamo un nuovo posto s e per tutti gli archi (t, s) e (s, t) di FN aggiungiamo nuovi archi (s, t) e (t, s), rispettivamente, tali che WN’ (s, t) = WN (t, s) e WN’ (t, s) = WN (s, t). Assumiamo la capacità KN’ (s) = KN (s). Per i nuovi posti s la marcatura iniziale MN’ (s) = KN (s) - MN (s). La rete risultante è senza contatti: per ogni marcatura raggiungibile M si ha MN’ (s) + MN’ (s) = KN’ (s). Date marcature M di N e M’ di N’ ogni transizione t è M-abilitata in N se e solo se è M’-abilitata in N’. Inoltre si possono sostituire tutte le capacità finite K N (s) N in N’ con w senza cambiare il comportamento di N’.

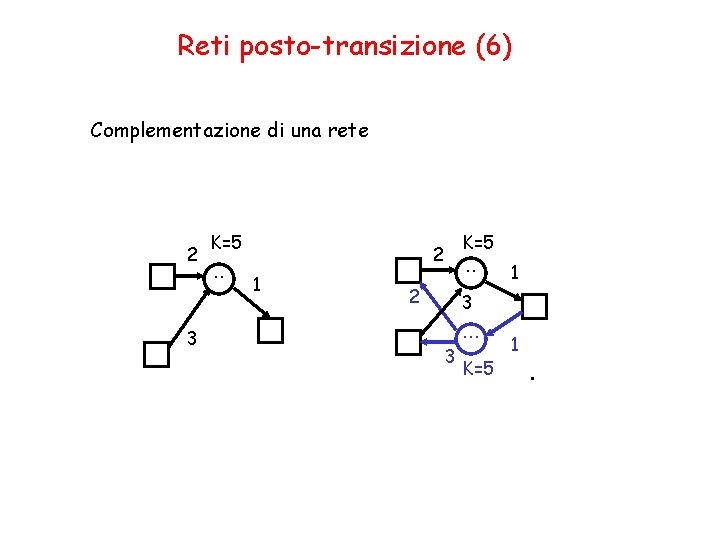
Reti posto-transizione (6) Complementazione di una rete 2 3 K=5. . K=5 2 1 . . 2 1 3. . . 3 K=5 1 .

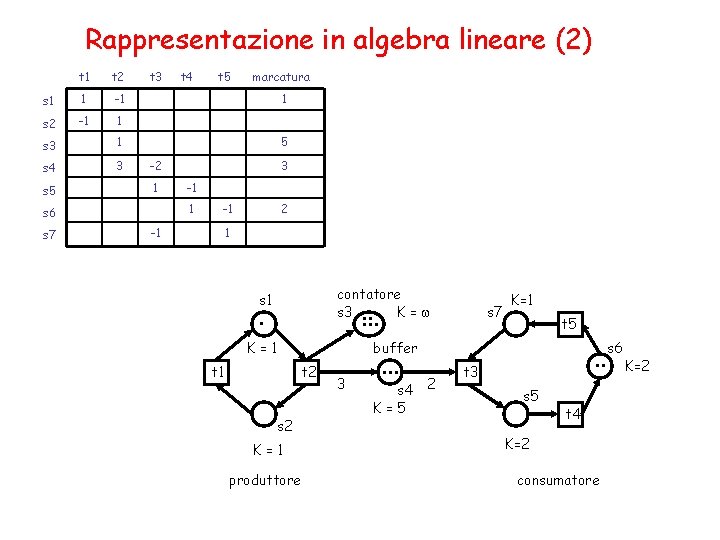
Rappresentazione in algebra lineare (1) Sia N = (S, T, F, K, M, W) una rete P/T. Per una transizione t T, sia il vettore t : S Z definito come: t (s) = W(t, s) se e solo se s t. . t t (s) = -W(s, t) se e solo se s . t t t (s) = W(t, s) - W(s, t) se e solo se s . t t (s) = 0 altrimenti . t. Sia la matrice N: S T Z definita come N(s, t) = t (s). Ogni marcatura può essere rappresentata da un vettore.

Rappresentazione in algebra lineare (2) t 1 t 2 s 1 1 -1 s 2 -1 1 s 3 1 s 4 3 s 5 t 3 t 5 marcatura 1 5 -2 1 3 -1 1 s 6 s 7 t 4 -1 -1 2 1 contatore s 3 K=w s 1 . . . K=1 t 1 K=1 produttore K=1 t 5 buffer t 2 s 7 3 . . . s 4 K=5 2 . . t 3 s 5 t 4 K=2 consumatore s 6 K=2

Rappresentazione in algebra lineare (3) La rappresentazione è non ambigua solo per reti pure. In questo caso possono essere derivate le componenti. Se si chiede anche N sia senza contatti il comportamento di N è pienamente determinato dalla matrice N e dal vettore MN. Corollario. Sia N una rete P/T e M, M’: SN N {w} due marcature di N. Allora per ogni transizione t TN 1. Se t è M-abilitato allora M [t> M’ M + t = M’ 2. 3. Se N è pura, allora anche : 2. t è M-abilitata 0 M + t KN 3. N è senza contatti M [MN> : (0 M + t KN ).

Rappresentazione in algebra lineare (4) Per reti con capacità infinita vale la seguente proprietà di monotonicità. Lemma. Sia N una rete P/T con s SN : KN (s) = w. Siano M 1, M 2: SN N {w} due marcature di N. Si ha 1. M 1 [t> M M 1+ M 2 [t> M + M 2 2. 2. M [M 1> M + M 2 [M 1 + M 2>

Grafo di copertura (1) Idea: rappresentare le (infinite) marcature raggiungibili mediante un grafo finito. I nodi del grafo rappresentano o “coprono” le marcature raggiungibili. Assumiamo senza perdere generalità KN (s) = w per ogni s SN. Ogni nodo E del grafo di copertura deve essere pensato come una marcatura della rete; alcuni nodi lo saranno, altri ricopriranno marcature raggiungibili. Vediamo come nascono sequenze infinite di marcature raggiungibili. Supponiamo M, M’ raggiungibili e M’ [M>. Supponiamo che per ogni posto s sia M(s) M’(s) e M M’ (scriviamo M < M’) e che KN (s) = w in tutti i posti dove M’(s) > M(s). Allora ogni transizione abilitata in M è anche abilitata in M’ e ripetendo la catena di transizioni che ha portato da M a M’ otteniamo una nuova marcatura M” con M’ < M”.

Grafo di copertura (2) Iterando si ha una sequenza di marcature distinte Mi, i = 1, 2, …, con la proprietà che Mi(s)=M(s) se M’(s)=M(s), mentre Mi+1(s)>Mi(s) se M’(s)>M(s). La sequenza sarà rappresentata nel grafo da un nodo di copertura H con H(s)=M(s) se M’(s)=M(s) e H(s) = w se il numero di token su s è crescente.

Grafo di copertura (3) Sia N una rete P/T con capacità infinite e sia G = G 0, G 1 , … la sequenza di grafi che soddisfa le richieste seguenti: 1. G 0 = ({MN}, ) 2. Sia Gi = (H, P). Sia E H e sia t TN tale che (a) t è E-abilitata (b) nessun arco da E è t-iscritto, ossia E’ tale che (E, t, E’) P. Allora definiamo la marcatura E~, per ogni s SN, con E~(s) = w se esiste un nodo E’ in H tale che E’ E+t e E’(s) < E(s) + t(s) ed esiste un cammino da E’ a E in Gi, E~(s) = E(s) + t (s) altrimenti, e sia Gi+1 = (H {E~}, P {(E, t, E~ )}).

Grafo di copertura (4) 3. Se non è possibile costruire Gi+1 seguendo 2 allora si ha Gi+1 = Gi. G è detta sequenza di copertura e G = ( Hi, Pi) è il grafo di copertura generato da G. Si noti che nella costruzione la marcatura può essere già contenuta in H, essendo un nodo di Gi. In questo caso in Gi+1 è aggiunto un nuovo arco (E, t, E~, ), ma non un nuovo nodo.

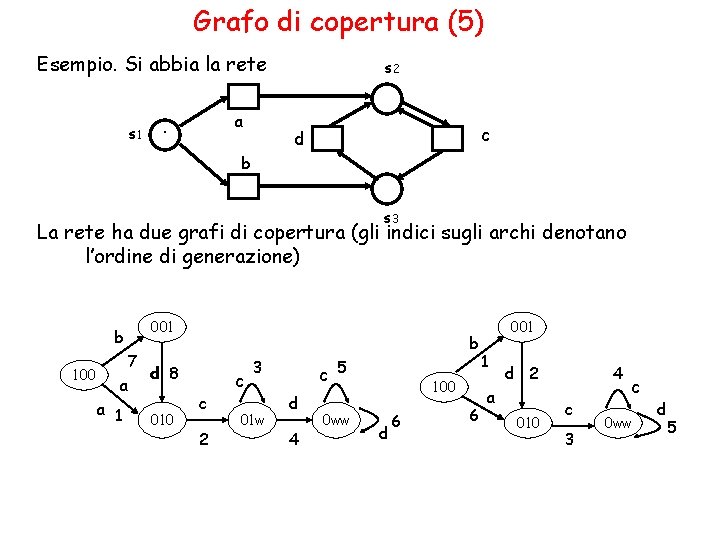
Grafo di copertura (5) Esempio. Si abbia la rete s 1 a . s 2 c d b s 3 La rete ha due grafi di copertura (gli indici sugli archi denotano l’ordine di generazione) b 100 001 7 d 8 a a 1 010 b c 2 c 3 01 w c 5 d 4 0 ww 100 d 6 6 001 1 d 2 a 010 4 c 3 c 0 ww d 5

Grafo di copertura (6) Ogni marcatura raggiungibile è coperta da un nodo del grafo di copertura. Lemma. Sia G un grafo di copertura di una rete P/T N. Per ogni sequenza MN [t 1> M 1 … Mn-1 [tn> Mn esiste un cammino E 0 t 1 E 1 … En-1 tn. En in G tale che MN = E 0 e per ogni i = 1, …, n Mi Ei. Sia N una rete P/T e E: SN N {w}. Sia E un nodo di G. 1. Sia (E)={s SN|E(s)=w} 2. Per i N una marcatura M di N è una i-marcatura se e solo se s (E) M(s) i e s (E) M(s) = E(s) 3. Sia ME [MN> un insieme minimale tale che per ogni i N esiste una i-marcatura M di E in ME. Allora ME è chiamato insieme di copertura di E.

Grafo di copertura (7) Lemma. Sia G un grafo di copertura di una rete P/T N. Per ogni E di G esiste un insieme di copertura ME. Teorema Ogni grafo di copertura di una rete P/T è finito.

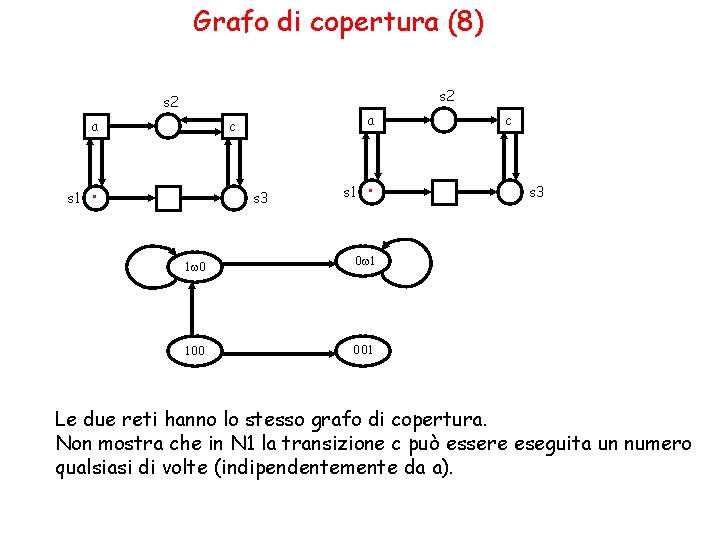
Grafo di copertura (8) s 2 a s 1 a c . s 3 s 1 . 1 w 0 0 w 1 100 001 c s 3 Le due reti hanno lo stesso grafo di copertura. Non mostra che in N 1 la transizione c può essere eseguita un numero qualsiasi di volte (indipendentemente da a).

Dimostrazione di proprietà con i grafi di copertura (1) Teorema Sia N una rete P/T, M: SN N {w} una marcatura arbitraria e G un grafo di copertura di N. Una marcatura M’ [MN> con M M’ esiste se e solo se 1. per ogni s SN, M(s) = w => MN(s) = w 2. esiste un nodo E in G tale che M E. Prova. Se MN(s) w allora per ogni M’ [MN> si ha M’ (s) w. Sia M’ [MN>, dato che esiste un nodo di G tale che M’ E, allora anche M E. Facilmente si vede il viceversa.

Dimostrazione di proprietà con i grafi di copertura (2) Sia N una rete P/T, S SN. L’insieme di posti S è simultaneamente illimitato se per ogni i N esiste Mi [MN> tale che per ogni s S Mi (s) i. Teorema Sia N una rete P/T, S SN e G un grafo di copertura di N. Allora S è simultaneamente illimitato se e solo se esiste un nodo E in G tale che ogni s S E(s) = w.

Dimostrazione di proprietà con i grafi di copertura (3) Sia N una rete P/T, M: SN N {w} una marcatura arbitraria e sia t TN. La transizione t è M-morta se per ogni M’ [MN> t non è M’-abilitata. Teorema Sia N una rete P/T, t TN e G un grafo di copertura di N. Allora t è MN-morta se solo se non esiste un arco (E, t, E’) in G. Teorema Sia N una rete P/T, t TN e G un grafo di copertura di N. Allora l’insieme [MN> di marcature raggiungibili è finito se e solo se nessun nodo di G ha una componente w.

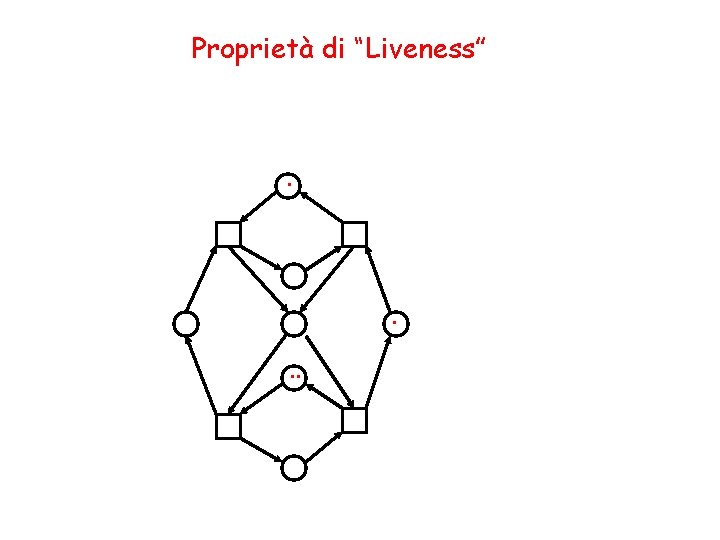
Proprietà di “Liveness” (1) In rappresentazioni di sistemi mediante reti, gli elementi attivi (processori, agenti, . . . ) sono rappresentati come transizioni, gli elementi passivi (buffer, memorie, . . . ) come posti e gli elementi assegnabili come token. Situazioni di blocco sono viste come transizioni che non possono piú essere eseguite. Queste reti non sono “vive”. Sia N una rete P/T, sia t TN 1. t è viva se e solo se per ogni M [MN> esiste M’ [M> tale che t e’ M’-abilitata. 2. N è viva se e solo se per ogni t TN, t è viva.

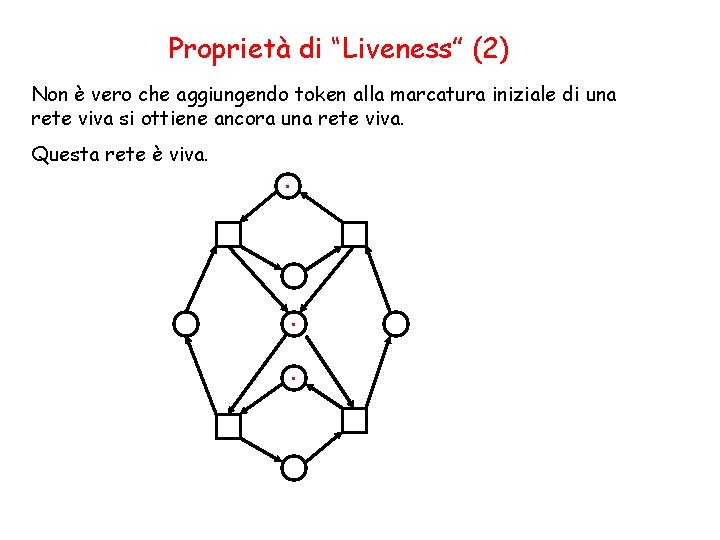
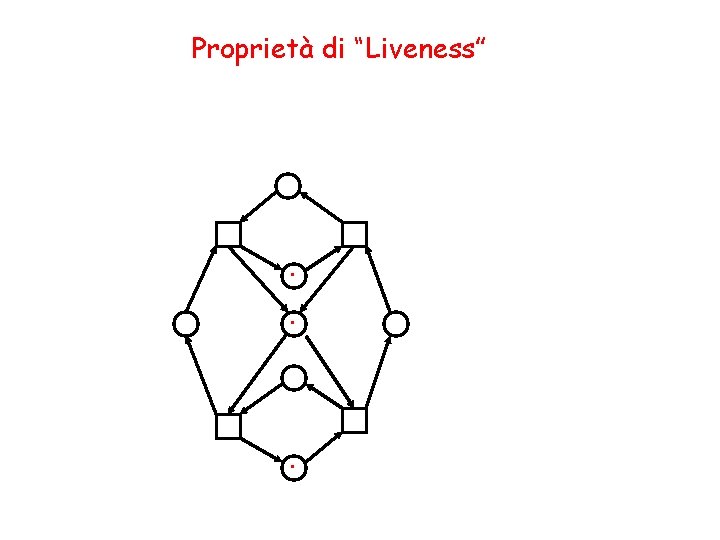
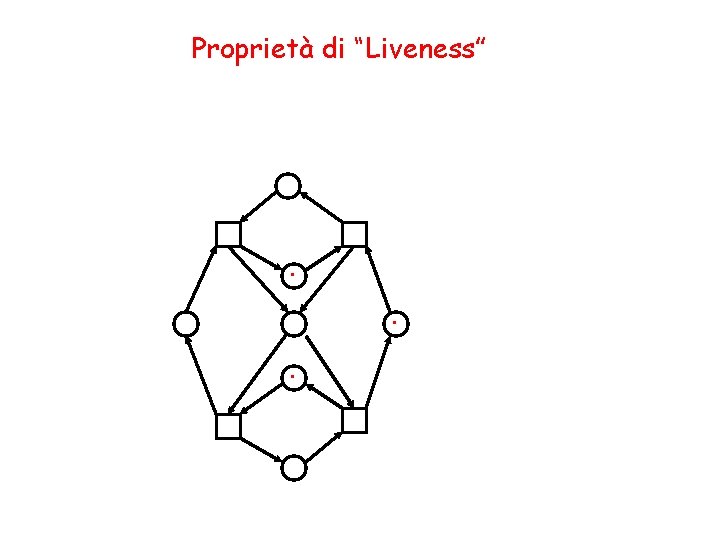
Proprietà di “Liveness” (2) Non è vero che aggiungendo token alla marcatura iniziale di una rete viva si ottiene ancora una rete viva. Questa rete è viva. .

Proprietà di “Liveness” . . .

Proprietà di “Liveness” . . .

Proprietà di “Liveness” . . .

Proprietà di “Liveness” . . .

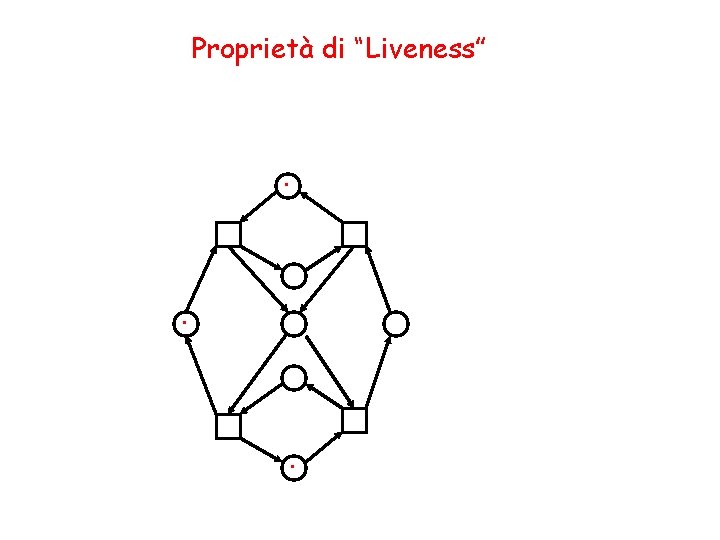
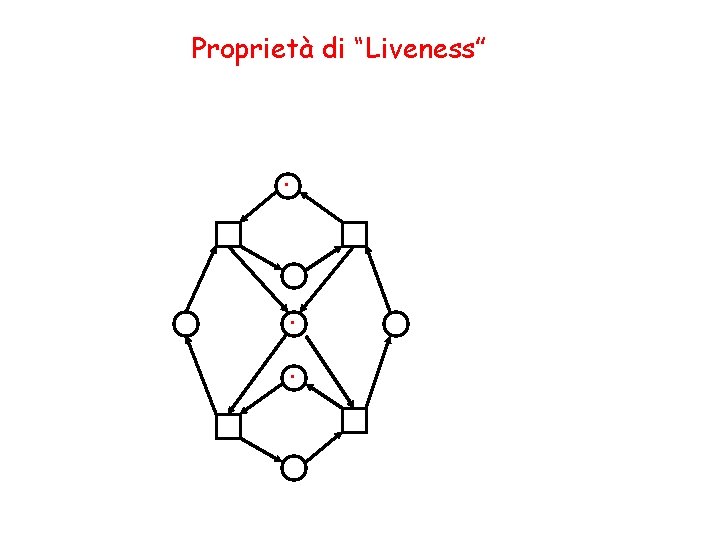
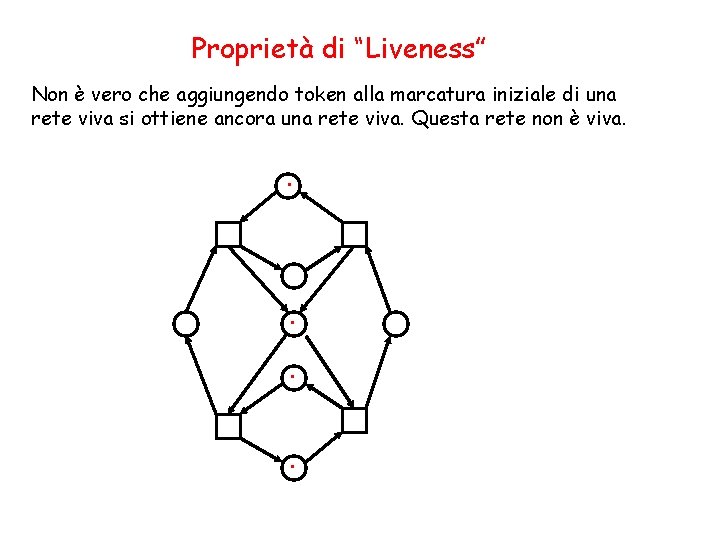
Proprietà di “Liveness” Non è vero che aggiungendo token alla marcatura iniziale di una rete viva si ottiene ancora una rete viva. Questa rete non è viva. . .

Proprietà di “Liveness” . .

Grafo di copertura (9) E` stato dimostrato che esiste una successione di reti di Petri con dimensioni linearmente crescenti tali che i corrispondenti grafi di copertura crescono rispetto al numero dei nodi piú velocemente di una qualsiasi funzione ricorsiva primitiva. Si ha di conseguenza che prese due reti P/T N, N’ con S N = SN’ è decidibile, ma non in tempo o spazio ricorsivo primitivo se [MN> = [MN>.

Problema della raggiungibilità Teorema. Data rete P/T N e una marcatura arbitraria M è decidibile se M [MN>.

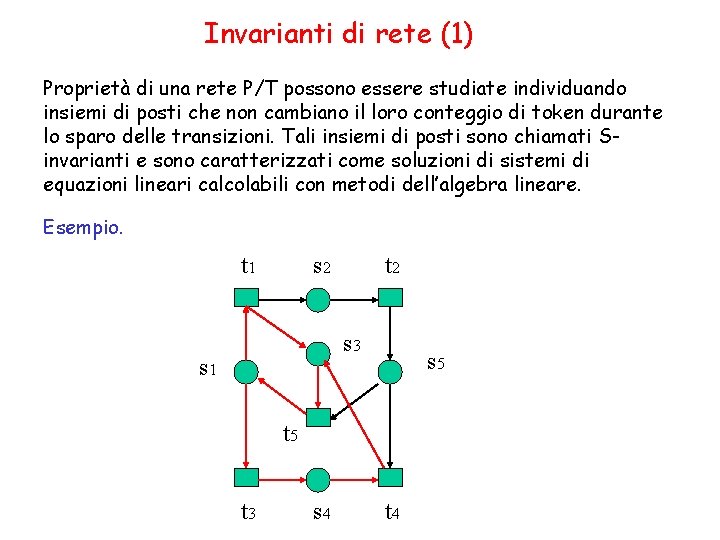
Invarianti di rete (1) Proprietà di una rete P/T possono essere studiate individuando insiemi di posti che non cambiano il loro conteggio di token durante lo sparo delle transizioni. Tali insiemi di posti sono chiamati Sinvarianti e sono caratterizzati come soluzioni di sistemi di equazioni lineari calcolabili con metodi dell’algebra lineare. Esempio. t 1 s 2 t 2 s 3 s 1 s 5 t 3 s 4 t 4

Invarianti di rete (2) Consideriamo una rete P/T N con peso degli archi 1. Vogliamo caratterizzare l’insieme dei posti S SN tale che non cambia il conteggio totale dei token quando le transizioni sparano. Se S è un. tale insieme di posti e s S allora per ciascuna transizione t s. che può essere abilitata ci deve essere un posto s’ t che è contenuto in S (intuitivamente un token fluisce lungo gli archi (s, t). e (t, s’) da s a s’). Analogamente per ogni transizione t s che può. essere abilitata ci deve essere un posto s’ t tale che un token fluisce lungo (s’, t) e (t, s) da s’ a s. Cosí S può essere caratterizzato da un insieme F di archi che soddisfa le richieste seguenti: 1) quando un arco appartenente a F parte o termina in un posto s allora tutti gli archi da e a s appartengono a F 2) per ciascun arco di F che termina in qualche transizione t c’è esattamente un arco appartenente a F che parte in t. Nell’esempio il conteggio dei token è costante per {s 1, s 2, s 4, s 5} e per {s 1, s 3, s 4}.

Invarianti di rete (3) Il metodo non funziona se ci sono pesi degli archi maggiori di 1. In questo caso se il conteggio su S SN non cambia quando spara una transizione t TN allora s . t SW(s, t) = s t. SW(t, s) che equivale a s. t S t(s) = - s t. S t(s) e anche a s. t S t(s) + s t. S t(s) = 0 e anche a s (. t t. ) S t(s) = 0 e a s S t(s) = 0. Se sostituiamo S con il suo vettore caratteristico c. S abbiamo s S t(s). c. S(s) = 0 o anche t. c. S = 0. N Se il conteggio su S SN non cambia sotto sparo di transizioni arbitrarie la condizione t. c. S = 0 deve essere soddisfatta per tutte le transizioni ti TN e quindi deve valere N’. c. S = 0 con N’ la trasposta di N. Viceversa ogni soluzione c di N’. x = 0 è vettore caratteristico di un insieme di posti conteggio costante.

Invarianti di rete (4) Data una rete P/T N un vettore i: SN Z è un S-invariante di N se N’. i = 0. Lemma. Se i 1, i 2 sono S-invarianti di una rete N e m Z anche m. i 1 e i 1 + i 2 sono S-invarianti di N.

Invarianti di rete (5) Esempio s 1 t 2 t 3 t 4 t 5 -1 -1 1 s 2 1 s 3 1 -1 1 s 4 s 5 i 1 1 -1 1 1 i 3 2 i 4 1 1 1 1 -1 i 2 1 1 1

Invarianti di rete (6) I vettori i 1 e i 2 sono vettori caratteristici e il fatto che siano Sinvarianti è interpretato che gli insiemi di posti {s 1, s 3, s 4} e {s 1, s 2, s 4, s 5} hanno un conteggio dei token costante. Possiamo dare un’interpretazione anche alle soluzioni che non sono vettori caratteristici. Il vettore i 3 ci dice che un token su s 1 conta quanto un token su s 2 e un token su s 3. Similmente un token su s 4 conta quanto un token su s 3 e un token su s 5. I token su s 1 e s 4 hanno un peso doppio rispetto ai token su s 2. S 3 e s 5. Se consideriamo questi pesi abbiamo conteggi di token pesati che rimangono costanti durante gli spari della rete.

Invarianti di rete (7) Siano M 1 e M 2 due marcature della rete dell’esempio e sia t una transizione tale che M 1 [t> M 2. Allora 2 M 1(s 1) + 2 M 1(s 4) + M 1(s 2) + M 1(s 3) + M 1(s 5) = 2 M 2(s 1) + 2 M 2(s 4) + M 2(s 2) + M 2(s 3) + M 2(s 5) Con l’invariante i 3 M 1. i 3 = M 2. i 3 Gli insiemi di posti conteggio costante dei token sono ottenuti da insiemi di archi che portano da un posto in. t a un posto in t. . Si ha il lemma seguente. Lemma. Sia N una rete P/T con un S-invariante positivo i e sia = {s SN | i(s) > 0}. Allora. S = S. . S

Invarianti di rete (8) Teorema. Sia N una rete P/T. Allora, per ciascun invariante i di N e ciascuna marcatura raggiungibile M [MN>, M. i = MN. i. Prova. Siano M 1, M 2 [MN> e t TN tale che M 1[t>M 2. Allora M 1 = M 2 + t e t. i = 0 perché i è un invariante. Perciò M 2. i = (M 1 + t ). i = M 1. i. L’inverso del teorema assume che ogni transizione possa sparare almeno una volta, e quindi è vero in particolare per reti vive. Teorema. Sia N una rete P/T viva e sia i: SN Z un vettore di posti tale che, per ogni M [MN>, M. i = MN. i. Allora I è un Sinvariante.

Invarianti di rete (9) Una rete P/T è coperta da S-invarianti se per ciascun posto s SN esiste un S-invariante positivo i di N con i(s) > 0. Corollar io. Se una rete P/T è coperta da S-invarianti esiste un invariante i con i(s) > 0 per ogni s SN. Prova. Dal fatto che la somma degli invarianti è un invariante. Una rete P/T è limitata se e solo se MN è finita ed esiste un n N tale che, per ogni M [MN> e s SN , n M(s). ma. Sia N una rete P/T e MN sia finita. Se N è coperta da invarianti allora N è limitata. Teore S-

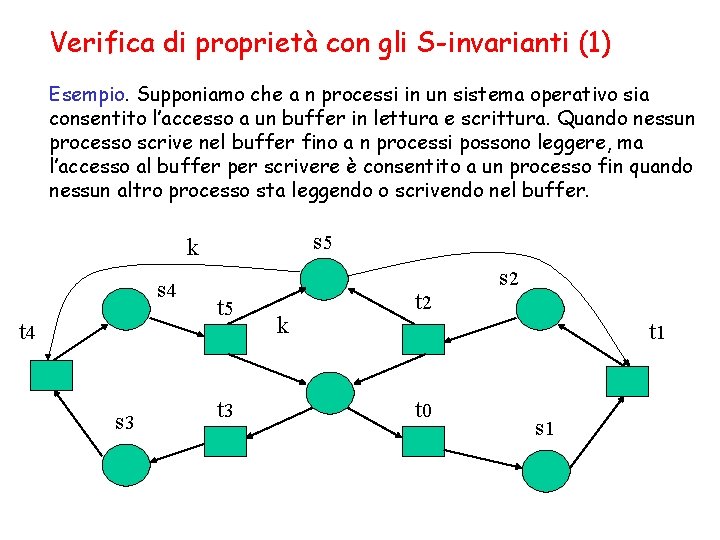
Verifica di proprietà con gli S-invarianti (1) Esempio. Supponiamo che a n processi in un sistema operativo sia consentito l’accesso a un buffer in lettura e scrittura. Quando nessun processo scrive nel buffer fino a n processi possono leggere, ma l’accesso al buffer per scrivere è consentito a un processo fin quando nessun altro processo sta leggendo o scrivendo nel buffer. s 5 k s 4 t 4 s 3 t 5 t 3 k t 2 s 2 t 1 t 0 s 1

Verifica di proprietà con gli S-invarianti (2) Ogni processo è in uno di cinque stati rappresentati dai posti s 0: processi inattivi, s 1: processi pronti a leggere, s 2: processi che leggono, s 3: processi pronti a scrivere, s 4: processi che scrivono, s 5: sincronizzazione. Nello stato iniziale tutti i processi sono inattivi, quindi in s 0 contiene n token. Il posto s 5 contiene k token, quanti sono i processi che possono leggere nel buffer concorrentemente. Quando siano state eventualmente effettuate fino a k letture fino a n processi possono scrivere nel buffer

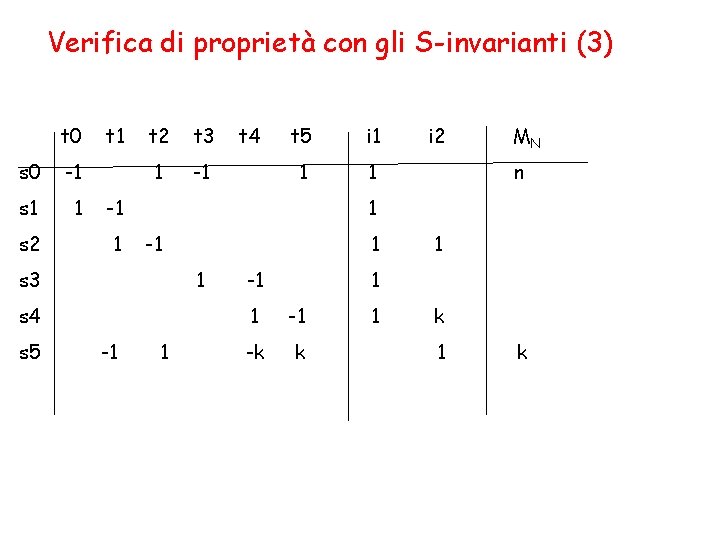
Verifica di proprietà con gli S-invarianti (3) t 0 s 0 -1 s 1 1 s 2 t 1 t 2 t 3 1 -1 t 5 i 1 1 1 -1 1 1 s 4 -1 i 2 MN n 1 s 3 s 5 t 4 1 -1 -k k 1 k

Verifica di proprietà con gli S-invarianti (4) Usando l’invariante i 1 abbiamo per ciascuna marcatura M [MN> 4 i 0 M(si) = 4 i 0 MN (si) = n Ossia il numero dei processi rimane costante e ogni processo è in uno degli stati s 0, s 1, s 2, s 3, s 4. Usando l’invariante i 2 abbiamo per ciascuna marcatura M [MN> M(s 2) + k. M(s 4) + M(s 5) = MN (s 2) + k. MN (s 4) + MN(s 5) = k Quindi s 4 contiene al piú un token sotto M, ossia un solo processo può scrivere. Quando s 4 ha un token s 2 e s 5 sono vuoti, ossia nessun processo può leggere il buffer. Il posto s 2 ha al più k token, ossia al più k processi leggono concorrentemente (questo avviene quando M(s 4)=0. Si può anche vedere che la rete è viva.