NECSI Summer School 2008 Week 3 Methods for

NECSI Summer School 2008 Week 3: Methods for the Study of Complex Systems Dynamical Systems and Phase Space Hiroki Sayama sayama@binghamton. edu

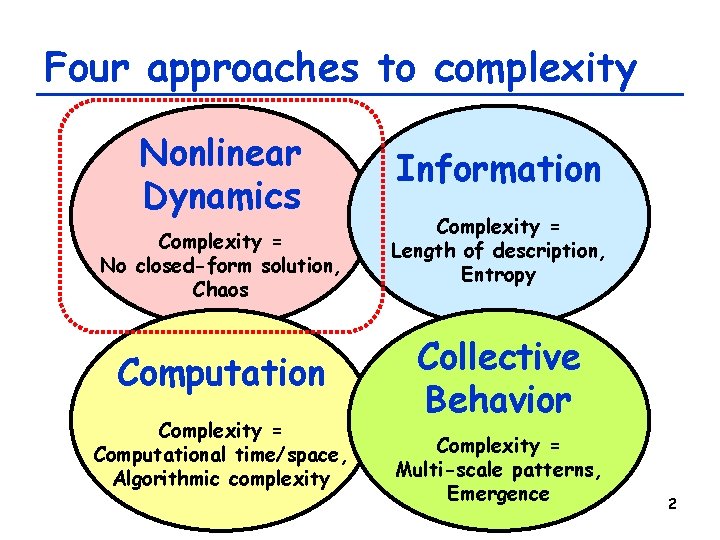
Four approaches to complexity Nonlinear Dynamics Complexity = No closed-form solution, Chaos Computation Complexity = Computational time/space, Algorithmic complexity Information Complexity = Length of description, Entropy Collective Behavior Complexity = Multi-scale patterns, Emergence 2

Mathematical formulations of dynamical systems • Discrete-time model: (difference/recurrence equations; iterative maps) xt = F(xt-1, t) • Continuous-time model: (differential equations) dx/dt = F(x, t) xt: State variable of the system at time t • May take “scalar” or “vector” value F: Some function that determines the rule that the system’s behavior will obey 3

Geometrical Approach to Dynamical Systems 4

Geometrical approach • Developed in the late 19 C by J. Henri Poincare • Visualizes the behavior of dynamical systems as trajectories in a phase space • Produces a lot of intuitive insights on geometrical structure of dynamics that would be hard to infer using purely algebraic methods 5

Phase space (state space) • A theoretical space in which every state of a dynamical system is mapped to a spatial location • Created by orthogonalizing state variables of the system; its dimensionality equals # of variables needed to specify the system state (a. k. a. degree of freedom) • Temporal change of the system states can be drawn in it as a trajectory 6

Attractor and basin of attraction • Attractor: A state (or a set of states) from which no outgoing edges or flows running in phase space – Static attractors (equilibrium points) – Dynamic attractors (e. g. limit cycles) • Basin of attraction: A set of states which will eventually end up in a given attractor 7

Visualizing Phase Space of Discrete Models 8

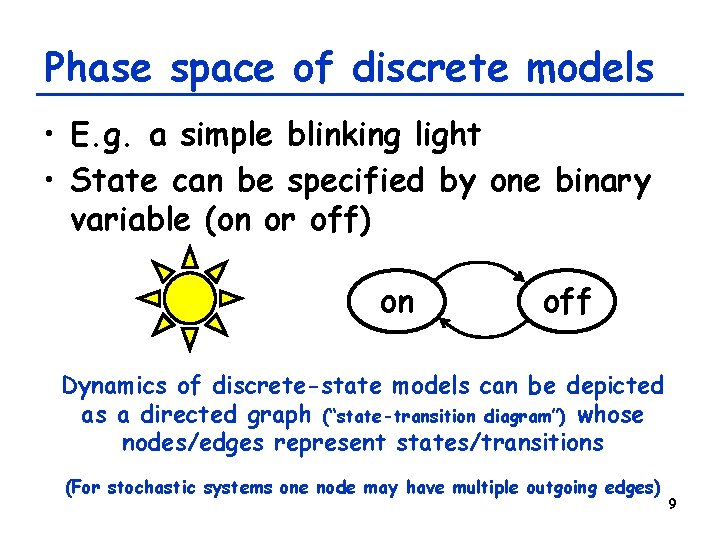
Phase space of discrete models • E. g. a simple blinking light • State can be specified by one binary variable (on or off) on off Dynamics of discrete-state models can be depicted as a directed graph (“state-transition diagram”) whose nodes/edges represent states/transitions (For stochastic systems one node may have multiple outgoing edges) 9

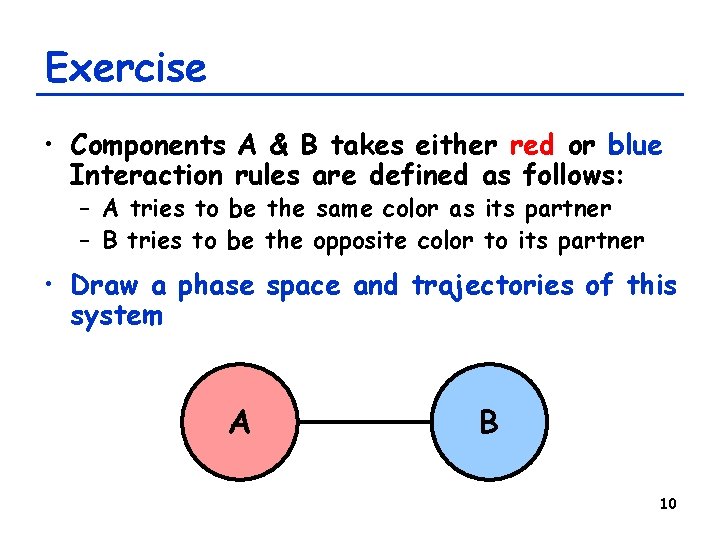
Exercise • Components A & B takes either red or blue Interaction rules are defined as follows: – A tries to be the same color as its partner – B tries to be the opposite color to its partner • Draw a phase space and trajectories of this system A B 10

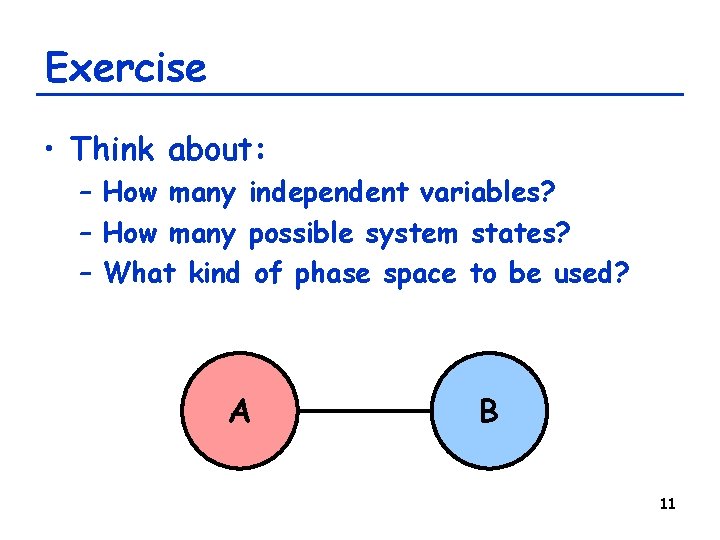
Exercise • Think about: – How many independent variables? – How many possible system states? – What kind of phase space to be used? A B 11

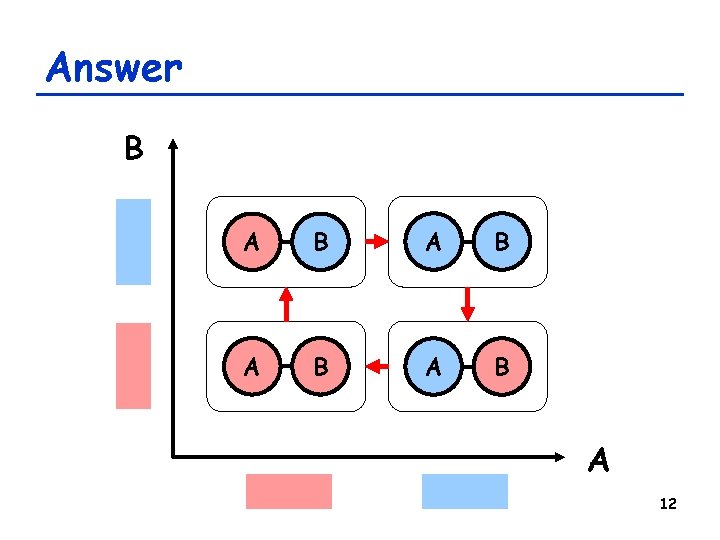
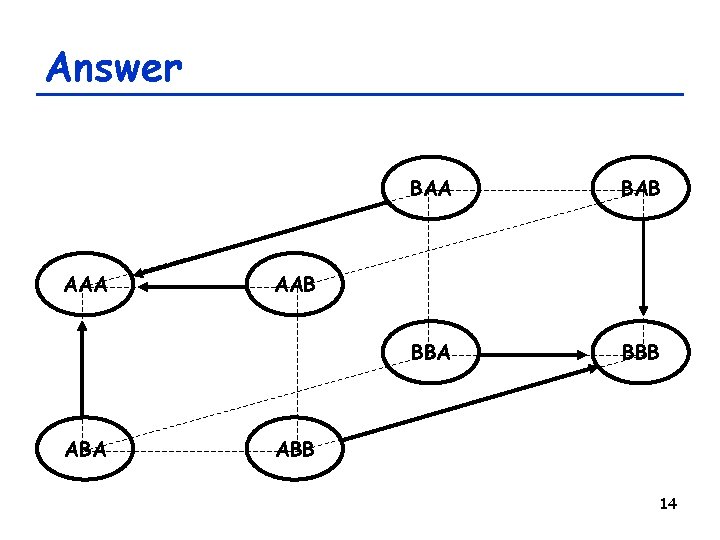
Answer B A B A B A 12

Exercise: Three-person majority game • There is a group made of three persons • Each person takes either option X or Y • Each person makes his/her choices open to the other two, then they simultaneously switch their choices to the major option within the group • This process repeats indefinitely • Illustrate geometrical structure of the phase space of this system and identify attractors and basins of attractions in it 13

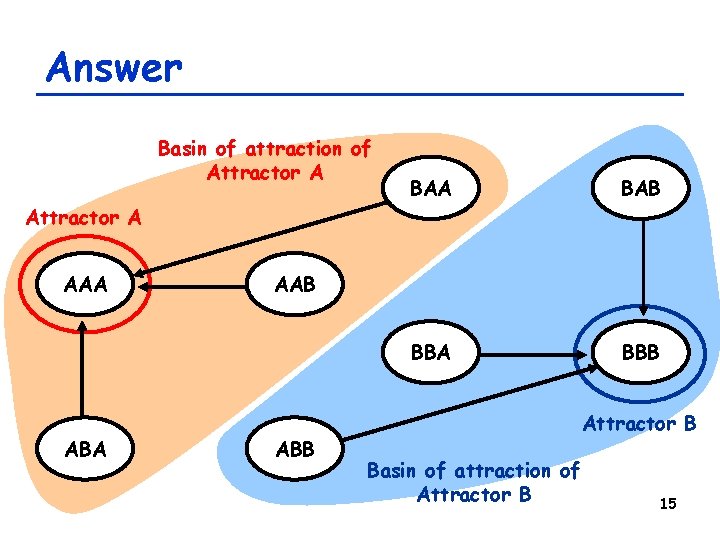
Answer AAA ABA BAB BBA BBB AAB ABB 14

Answer Basin of attraction of Attractor A BAB BBA BBB Attractor A AAA ABA AAB ABB Attractor B Basin of attraction of Attractor B 15

Exercise • Illustrate geometrical structure of the phase space of a three-person minority game (i. e. , each person switches his/her choice against the major option within the group) 16

Answer Dynamic attractor AAA ABA BAB BBA BBB AAB ABB There is only one basin 17 of attraction in this case

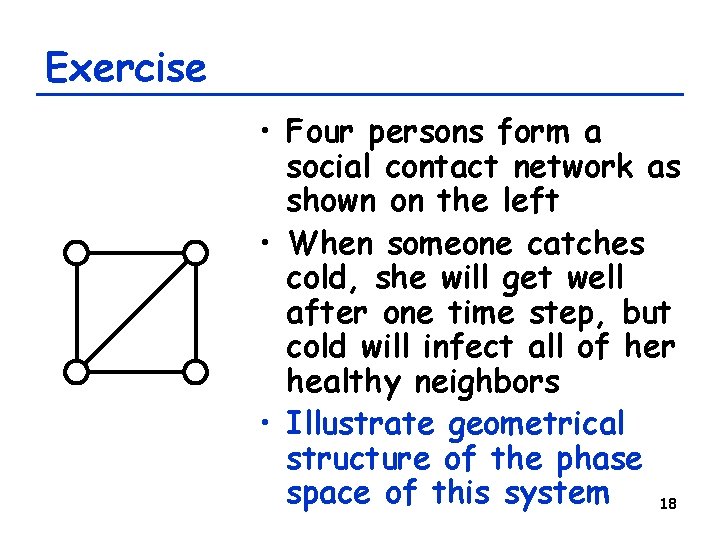
Exercise • Four persons form a social contact network as shown on the left • When someone catches cold, she will get well after one time step, but cold will infect all of her healthy neighbors • Illustrate geometrical structure of the phase space of this system 18

Reducing the number of states • In some cases, it may be possible to reduce the number of possible states by using symmetries – – Rotational Reflectional Translational Graph isomorphism etc. 19

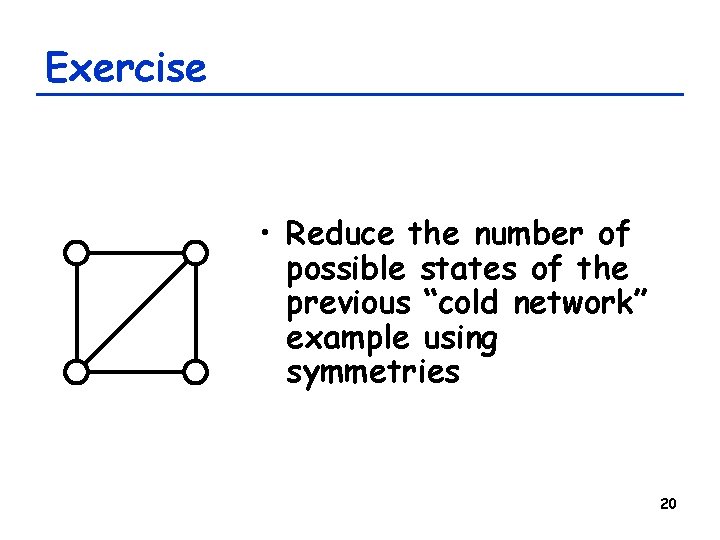
Exercise • Reduce the number of possible states of the previous “cold network” example using symmetries 20

Visualizing Phase Space of Continuous Models 21

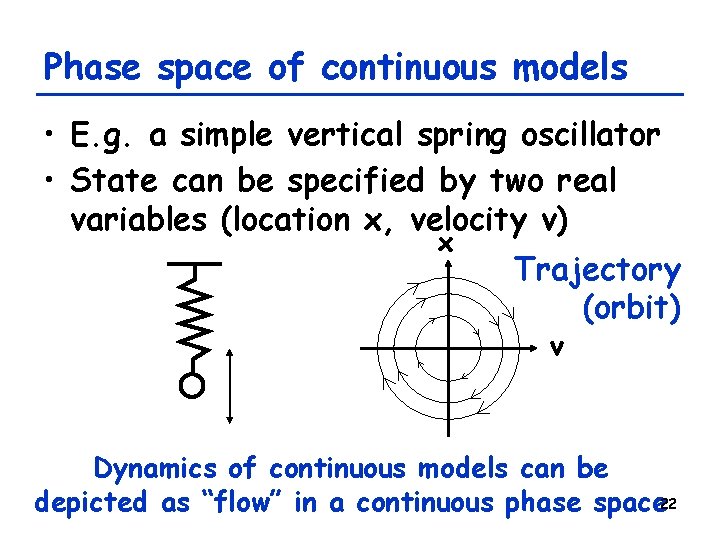
Phase space of continuous models • E. g. a simple vertical spring oscillator • State can be specified by two real variables (location x, velocity v) x Trajectory (orbit) v Dynamics of continuous models can be depicted as “flow” in a continuous phase space 22

Visualizing phase space of continuous models manually • Find “nullclines” – Points in the phase space where one of the derivatives is zero (i. e. , trajectories are in parallel to one of the axes) – Plot where the nullclines are – Find how the sign of the derivative changes across the nullclines – Find values of other non-zero derivatives • Draw a “flow” between those nullclines with curves that don’t intersect with each other 23

Exercise • Draw an outline of the phase space of the following system by studying the distribution of its nullclines: dx/dt = x – x y dy/dt = y – x y (x >= 0, y >= 0) 24

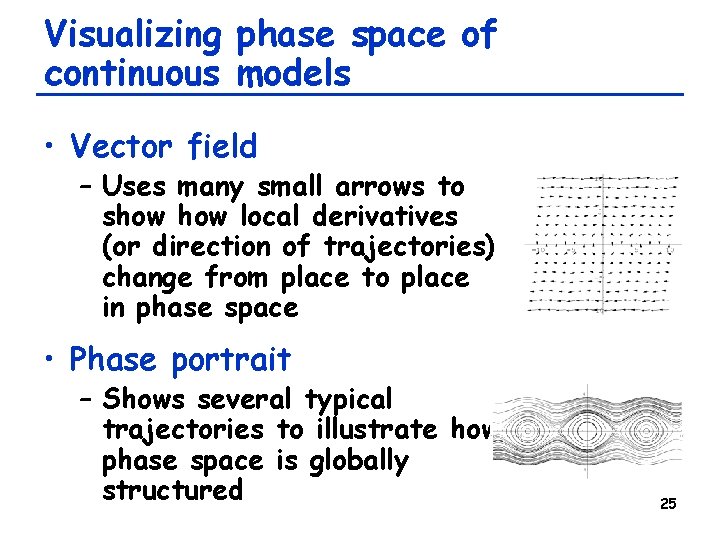
Visualizing phase space of continuous models • Vector field – Uses many small arrows to show local derivatives (or direction of trajectories) change from place to place in phase space • Phase portrait – Shows several typical trajectories to illustrate how phase space is globally structured 25

Exercise: Draw a phase space of the SIR model • “Susceptible” individuals can turn into “Infective” by contacting other “Infectives” • “Infective” individuals turn into “Removed” at a given rate – d. S/dt = -i S I – d. I/dt = i S I – r I – d. R/dt = r I 26

Exercise: Draw a phase space of the RPS model • Assume a cyclic food chain among three species so that “Rock” eat “Scissors”, “Scissors” eat “Paper”, and “Paper” eat “Rock” • Each species will increase by eating other species and decrease by being eaten by others – d. R/dt = a R S – b R P – d. P/dt = b R P – c S P – d. S/dt = - a R S + c S P 27

Summary: Advantage of geometrical approach • By using phase space, one can convert dynamic behaviors of systems into a static picture • By identifying geometrical structure of phase space such as attractors and basins of attraction, one can visually describe possible final states of the system and its sensitivity to initial conditions 28

Linear Systems 29

Linear systems • Linear systems are the simplest cases where states of nodes are continuousvalued and their dynamics are described by a time-invariant matrix • Discrete-time: xt = A xt-1 • Continuous-time: dx/dt = B x – A / B are called “coefficient” matrices – We don’t consider constants (as they can be easily converted to the above forms) 30

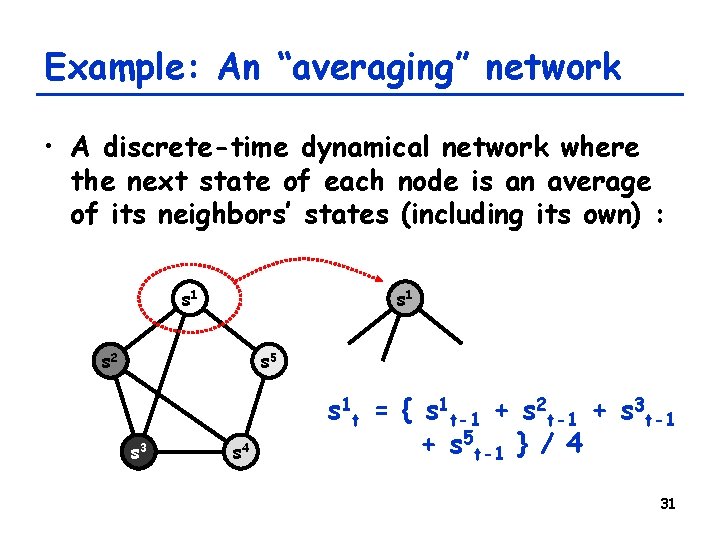
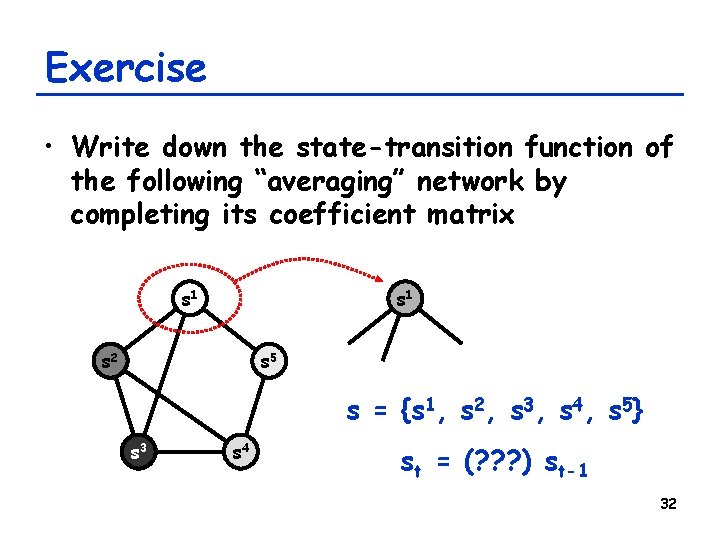
Example: An “averaging” network • A discrete-time dynamical network where the next state of each node is an average of its neighbors’ states (including its own) : s 1 s 2 s 5 s 3 s 4 s 1 t = { s 1 t-1 + s 2 t-1 + s 3 t-1 + s 5 t-1 } / 4 31

Exercise • Write down the state-transition function of the following “averaging” network by completing its coefficient matrix s 1 s 2 s 5 s = {s 1, s 2, s 3, s 4, s 5} s 3 s 4 st = (? ? ? ) st-1 32

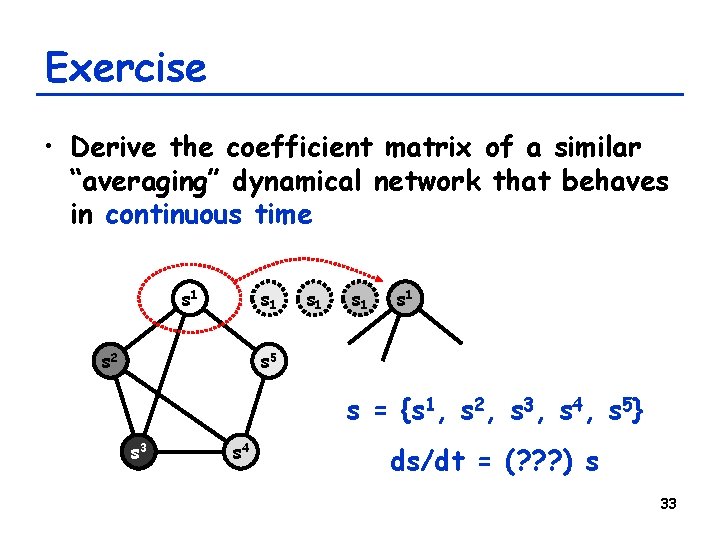
Exercise • Derive the coefficient matrix of a similar “averaging” dynamical network that behaves in continuous time s 1 s 2 s 1 s 1 s 5 s = {s 1, s 2, s 3, s 4, s 5} s 3 s 4 ds/dt = (? ? ? ) s 33

Coefficient matrix and adjacency matrix • Coefficient matrices are very similar to adjacency matrices of graphs: – If there is no interaction (= no edge) between nodes j and i, then aij = 0 – A weight aij in an adjacency matrix corresponds to the strength of influence from node j to i – One difference: A coefficient matrix may take negative components in it 34

Equilibrium points of linear systems • Discrete-time: • Continuous-time: xt = A xt-1 dx/dt = B x • Linear systems have the origin (x=0) as a trivial equilibrium point • Can they have other non-trivial (nonzero) equilibrium points? 35

Finding equilibrium points • Discrete-time: • Continuous-time: xt = A xt-1 dx/dt = B x • Discrete-time: • Continuous-time: xe = A xe 0 = B xe • If A has 1 (or if B has 0) as its eigenvalue, then the corresponding eigenvector(s) show the system’s equilibrium point(s) 36

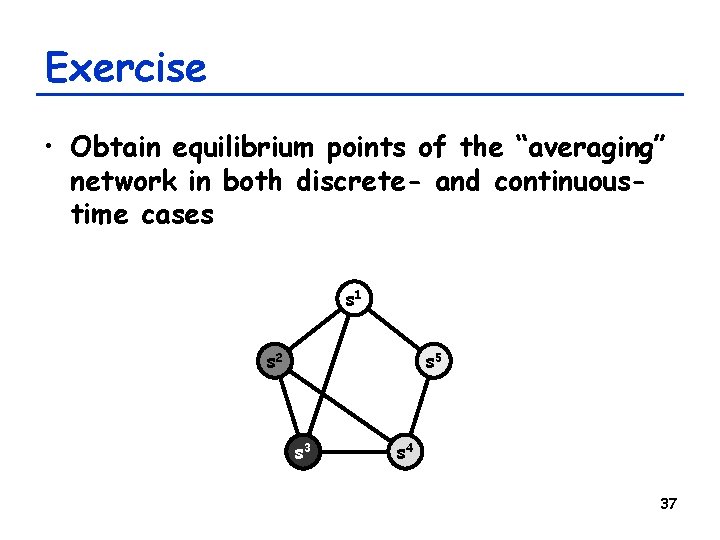
Exercise • Obtain equilibrium points of the “averaging” network in both discrete- and continuoustime cases s 1 s 2 s 5 s 3 s 4 37

Asymptotic Behavior of Linear Systems 38

Where will the system go eventually? • Discrete-time: xt = A xt-1 • Continuous-time: dx/dt = B x These equations give the following exact solutions: • Discrete-time: xt = At x 0 • Continuous-time: xt = e. Bt x 0 = { I + Sk=1~ (Bt)k/k! } x 0 39

FYI: Exponential operator for matrices • xt = e. Bt x 0 = { I + Sk=1~ (Bt)k / k! } x 0 – Similar to the Taylor series expansion of the exponential function: ex = 1+ x 2/2! + x 3/3! + … – e. M converges for any square matrix M – If M’s eigenvalues are {li }, then e. M’s eigenvalues are { el }, with all eigenvectors unchanged (you can prove this) i 40

Where will the system go eventually? • Discrete-time: xt = A xt-1 • Continuous-time: dx/dt = B x • What happens if the system starts from non-equilibrium initial states and goes on for a long period of time? • Let’s think about their asymptotic behavior lim t-> xt !! 41

Considering asymptotic behavior (1) • Let { vi } be n linearly independent eigenvectors of the coefficient matrix (They might be fewer than n, but here we ignore such cases for simplicity) • Write the initial condition using eigenvectors, i. e. x 0 = b 1 v 1 + b 2 v 2 +. . . + bnvn 42

Considering asymptotic behavior (2) • Then: xt = At x 0 (discrete-time) = l 1 t b 1 v 1 + l 2 t b 2 v 2 + … + l nt bnv n or xt = e. Bt x 0 (continuous-time) = el 1 t b 1 v 1 +el 2 t b 2 v 2 + … +elnt bnvn 43

Dominant eigenvector (1) • Discrete-time: If |l 1| > |l 2|, |l 3|, …, xt = l 1 t { b 1 v 1 + (l 2/l 1)t b 2 v 2 +. . . + (ln/l 1)t bnvn } lim t-> xt ~ l 1 t b 1 v 1 • Continuous-time: If Re(l 1) > Re(l 2), Re(l 3), …, xt = el 1 t { b 1 v 1 +e(l 2 -l 1)t b 2 v 2 +. . . +e(ln-l 1)t bnvn } lim t-> xt ~ el 1 t b 1 v 1 If the system has just one such dominant eigenvector v 1, its state will be eventually along that vector 44 regardless of where it starts

Dominant eigenvector (2) • If the system has just one such dominant eigenvector v 1, its state will be eventually along that vector regardless of where it starts • But divergence or oscillation are possible • If, additionally, l 1=1 (discrete-time) or 0 (continuous-time), then the system will eventually reach the equilibrium point (If the system has multiple dominant eigenvectors, final states may depend on initial states) 45

FYI: What eigenvalues and eigenvectors can tell us • An eigenvalue tells whether a particular “state” of the system (specified by its corresponding eigenvectors) grows or shrinks by interactions between parts – | l | > 1 -> growing for discrete-time cases – | l | < 1 -> shrinking – Re(l) > 0 -> growing for continuous-time cases – Re(l) < 0 -> shrinking 46

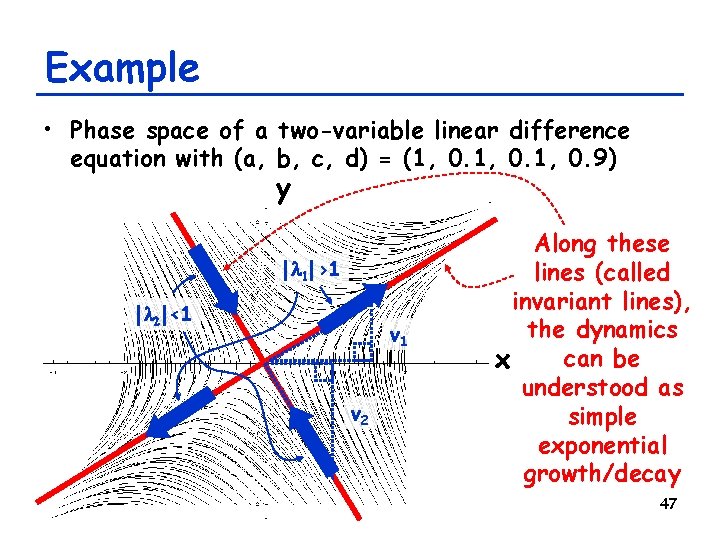
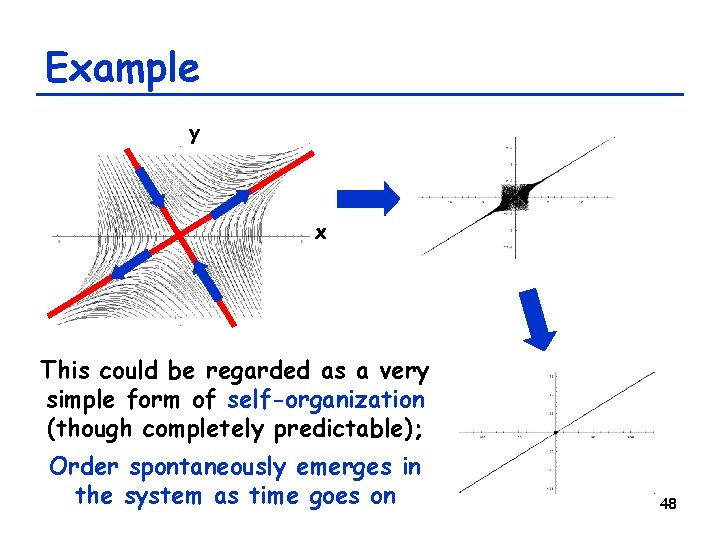
Example • Phase space of a two-variable linear difference equation with (a, b, c, d) = (1, 0. 9) y |l 1|>1 |l 2|<1 v 2 Along these lines (called invariant lines), the dynamics can be x understood as simple exponential growth/decay 47

Example y x This could be regarded as a very simple form of self-organization (though completely predictable); Order spontaneously emerges in the system as time goes on 48

Exercise • Calculate eigenvalues of the following linear system and predict its dynamics along the lines given by the eigenvectors xt = 2 xt-1 - 2 yt-1 yt = 0. 2 xt-1 + 0. 2 yt-1 • Draw its phase space to confirm your prediction 49

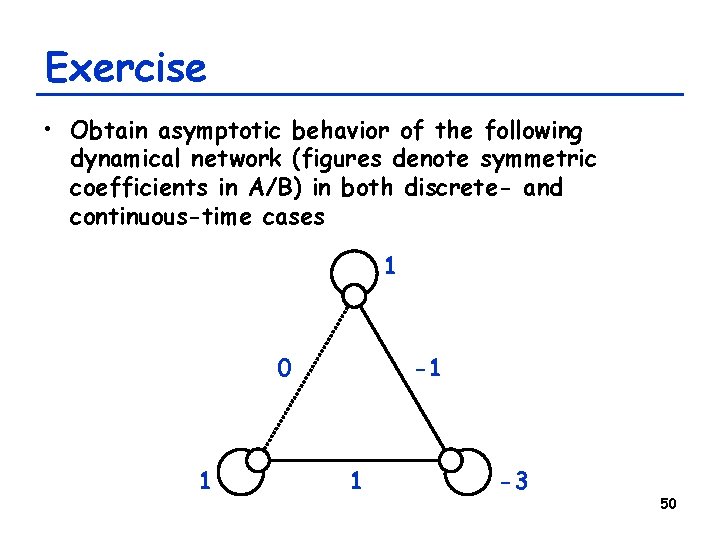
Exercise • Obtain asymptotic behavior of the following dynamical network (figures denote symmetric coefficients in A/B) in both discrete- and continuous-time cases 1 -1 0 1 1 -3 50

FYI: Symmetry of matrices and type of eigenvalues • If the matrix is symmetric, it has real eigenvalues only, so the asymptotic behavior should be either converging, diverging, or flipping • If the matrix is asymmetric, it may have complex eigenvalues and thus the system may keep changing dynamically in rotational trajectories 51

Summary (1) • To find equilibrium points of a linear dynamical system, calculate the eigenvectors of its coefficient matrix with its corresponding eigenvalue: – l= 1 (for discrete-time cases) – l= 0 (for continuous-time cases) 52

Summary (2) • To study asymptotic behavior of a linear dynamical system, check if its coefficient matrix has just one dominant eigenvector whose corresponding eigenvalue l 1 satisfies: – |l 1| > |l 2|, |l 3|, . . . (for discrete-time cases) – Re(l 1) > Re(l 2), Re(l 3), . . . (for continuous-time cases) 53

Summary (3) • If the system has just one such dominant eigenvector, its state will be eventually along that vector regardless of where it starts • These final states may oscillate and/or diverge in its magnitude, but if its corresponding eigenvalue = 1 (discrete-time) / 0 (continuous-time), the final state is also an equilibrium point 54

Nonlinear Systems 55

Nonlinear systems • Nonlinear systems are systems whose dynamics cannot be written in a linear (i. e. , matrix & vector) form because of nonlinear terms in F • Discrete-time: xt = F(xt-1, t) • Continuous-time: dx/dt = F(x, t) 56

Example: Logistic growth • N: Population • r: Population growth rate • K: Carrying capacity 1 0. 8 0. 6 0. 4 0. 2 2 4 6 • Discrete-time version: Nt = Nt-1 + r Nt-1 ( 1 – Nt-1/K ) 8 10 • Continuous-time version: Non-linear terms d. N/dt = r N ( 1 – N/K ) 57

Example: Lotka-Volterra model • Independently derived by A. J. Lotka (1925) and V. Volterra (1926) • A well-known nonlinear model of a simple ecosystem made of predator and prey populations 58

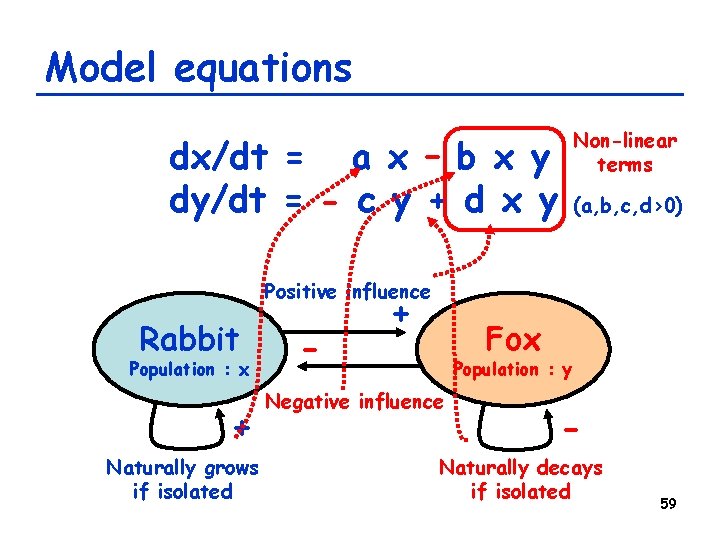
Model equations Non-linear terms dx/dt = a x – b x y dy/dt = - c y + d x y (a, b, c, d>0) Positive influence Rabbit Population : x + Naturally grows if isolated - + Fox Population : y Negative influence - Naturally decays if isolated 59

Revision 1: With carrying capacity • How can you introduce a limited carrying capacity for the growth of rabbits to the equations? dx/dt = a x – b x y dy/dt = - c y + d x y 60

Revision 1: With carrying capacity • How can you introduce a limited carrying capacity for the growth of rabbits to the equations? dx/dt = a x (1 -x/K) – b x y dy/dt = - c y + d x y – Obtain equilibrium points and draw phase space (with a=b=c=d=1, K=2) 61

Revision 2: With bounded predation rate • A fox can’t eat 100 rabbits at once no matter how many there around • How can you set an upper bound to the predation rate in the equations? dx/dt = a x (1 -x/K) – b x y dy/dt = - c y + d x y 62

Revision 2: With bounded predation rate • A fox can’t eat 100 rabbits at once no matter how many there around • How can you set an upper bound to the predation rate in the equations? dx/dt = a x (1 -x/K) – b Jx/(J+x) y dy/dt = - c y + d Jx/(J+x) y – Obtain equilibrium points and draw phase space (with a=b=c=d=1, K=2, J=3) 63

Summary • Systems’ dynamics may be visualized and studied using phase spaces • Linear systems’ dynamics may be studied through eigenvalue analysis – Equilibrium points – Asymptotic behavior • Realistic model assumptions are likely to make the dynamics nonlinear 64