Mathematics The music of the reason Music mathematics

Mathematics: The music of the reason, Music: mathematics of sense. Prof. Dr. Emilio Lluis-Puebla

Introduction n Aplicability n Lenguage n Mathematical research

Characteristics of Mathematics n Diffícult to describe or define its subject matter n Perfect logic n The conclusiveness of Mathemátics n Independence

What does the word Mathematics mean? n Mathema = scholarship n Manthánein= the infinitive of learning n Mendh = science, knowledge n Is the relative to learning n Implicit sense, Mathematics = “what is worthy to be learned"

What is Mathematics?

Some mathematical problems n Fermat Theorem n x 2+y 2=z 2 n xn+yn=zn n Four color problem n New ideas progress in mathematics

What is mathematical research? n Alternative on mathematical theory and problem solving n Human activity n Mathematical Theory

How is innovation in Mathematics achieved? n The creation of new methods or technics constitute mathematical innovation n Galois Symmetry Group Theory n Cohesion to a mathematical theory n Problems in other disciplines n Usual Methods – new concepts and problems

One example: Algebraic Kn n Theory. A commutative monoid without zero divisors can be considered within the commutative group it generates. 1957 Grothendieck To a commutative monoid M associate a commutative group K(M), unique up to isomorphism, and a canonical monoid homomorphism j: M K(M) such that for any commutative group G, any monoid homomorfism f: M G factors in a unique way as f: M K(M) G. n

n Grothendieck´s group 1958. n 1959 Atiyah and Hirzebruch. They applies the construction to the aditive monoid of isomorphism clases of complex vector bundles with base space a CW-complex X. n Grothendieck´s group K 0(X). K-n(X). n n Bott´s periodicity Kn(X) » Kn+2(X) and is used to define Kn(X) for nÎZ. Topological K-Theory. Atiyah-Singer´s Theorem

n n Serre´s result, Swan, 1962. Translate topological concepts into algebraic concepts. The category of vector bundles over X is equivalent to the category of finately generated projective Lmodules where L=C(X). Definition of K(L) or K 0(L) that makes sense for any ring L, as the Grothendieck group of the category of finately generated projective L-módulos. K 0(L) L-projective modules.

n n Serre´s problem, 1955. Are the finately generated projective modules over k[t 1, t 2, . . . tn] free?

n Quillen and Suslin. n Conjeture of Serre. Algebraic K-Theory.

Bass Emilio Lluis-Puebla & Hymann

n In 1964, Hymann Bass defined the funtor K 1 n Whitehead en 1939 y 1950. K 1(Z[G]) n K 1(L) = GL(L)/[GL(L), GL(L)] =H 1(GL(L), Z) n Congruent subgroup problema in 1967, Bass. Milnor-Serre for the special linear group of a ring of integers in a numeric field.

n Emilio Lluis-Puebla & John Milnor

n n n In 1969, Milnor defined the functor K 2 as the kernel of the epimorphism from the Steinberg group St(L) to the elementary matrices E(L); i. e. ker {St(L) E(L)} Kervaire in 1970 proves that St(L) is the central universal extensión of E(L), and hence K 2(L) can be described as the Schur multiplier of the perfect group E(L). K 2(L)=H 2(E(L), Z)

n n n Matsumoto calculated K 2 of a field Bass and Tate to describe K 2 of numeric fields. Algebraic K-Theory is a multidisciplinary fenomena within Mathematics.

n n Quillen defined, for i ³ 1, Ki. L= pi(BGLL+). As in the i=1, 2, cases Ki is a covariant functor from the category of rings to the category of groups. n On one side, Algebraic K-Theory introduced topological methods to define algebraic invariants, such as the higher K-groups of rings. On the other hand, it provides a way of translating algebraic concepts into topological concepts. Algebraic Ktheory studies the properties of the groups Ki(L), constructed from a ring L.

n n n Calculation of the groups Ki for diverse rings. Bass, Milnor, Karoubi, Quillen, Weibel, Loday, Soulé, Snaith, Bass proved in 1968 that K 1 Z @ Z/2 and that K 1(Z/p 2)=ZÅZ/p-1, p a primo different from 2. Milnor proved in 1971 that K 2 Z @ Z/2 and that K 2(Z/p 2)= 0 for a prime p different from 2. In 1972 Quillen calculated the algebraic K-theory of a finete field.

n n Lee y Sczarba found in 1976 that K 3 Z @ Z/48. Let R be the ring of integers in a numerical field and I a non trivial ideal. Calculating Ki(R/I) for finite rings is an open problema for i ³ 3. n Evens-Friedlander n Aisbett, Lluis-Puebla, Snaith y Soulé

n Milnor´s conjecture Vladimir Voevodsky n p different than two Bloch-Kato´s conjecture Voevodsky y Rost.

n n=2 mod 4 the finite groups Kn(Z) are cyclic for n<20, 000. Fields medal Serre (1954), Milnor (1962), Grothendieck (1966), Atiyah (1966), Quillen (1978), Connes (1982) y Voevodsky (2002). n

Mathematics, a “Fine Art” n n n Beauty and truth have equal esteem Elegance in style Economy of effort Clarity of thought Perfection in the detail and in how to achieve a forceful and convincing deduction.

Aesthetic characteristics of Mathematics n n n Universality Simple and concise arguments Selection and formulation of problems

Henri Poincaré (1854 -1912)

Formalism and mathematical rigor n Formal mathematics n Transmission of mathematics n Mathematical rigor n Essence of mathematics is to bring two seemingly disparate fields together

How do we do mathematics? n Individually n In group

What kind of mathematicians are there in general? n Brute force n Elegants n Both forms

How is mathematics transmitted today? n n At levels of younger people New abstract concepts absorb other ones created in the past

How a problem is selected in order to do research? n n n Comunnication with other collegues Curiosity Meditate and move around the mathematical literature properly

What is known as Applied Mathematics? n Applications outside their own field n Multidisciplinary

An example: Mathematical Music Theory n Pythagoras

n n n "musicologie“ "musikwissenschaft" which means “science of music" One of the main purposes of Mathematical Music Theory is to establish a stable framework, defining the concepts in a precise way.

Mathematical Music Theory of Guerino Mazzola n n One of the main goals of Mathematical Music Theory is to develop a scientific framework for Musicology

Guerino Mazzola and Emilio Lluis-Puebla in 1997, Mexico City. n

n n Mathematical Music Theory is based on the Theories of Groups, Modules and Categories, in Algebraic Topology and Combinatorics, in Algebraic Geometry and Representation Theory, among others. Its purpose is to describe the musical structures.

n Three major paradigms of Mathematics and Musicology that have occurred during the 150 years that have been parallel in the evolution of both and the growing presence of mathematics in Music. n Global structures n Symmetries n Philosophy of Yoneda

n n n Mazzola in his "Status Quo 2000“, explains why the approach by his geometric theoretical model of that time developed into a framework that is appropriate for many musical problems. This new framework is based on more sophisticated mathematics such as Category and Topos Theory Within this area, high-level mathematics is carried out, not just applications, that is, new mathematics is created, mathematical results are tested within the defined objects.

In 2007 Guerino Mazzola *Presents a new categorical framework describing the relationship between musical and mathematical activities. *This relationship can be described in terms of adjoint functors.

Category Theory Daniel Kan in 1958: adjoint functors

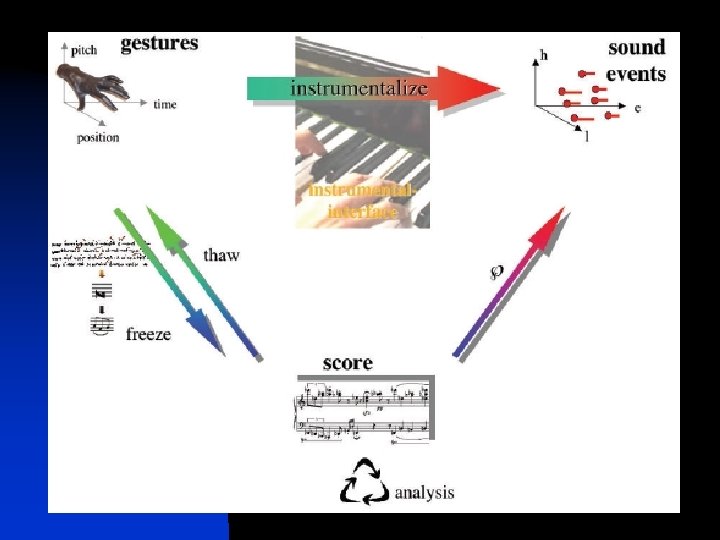
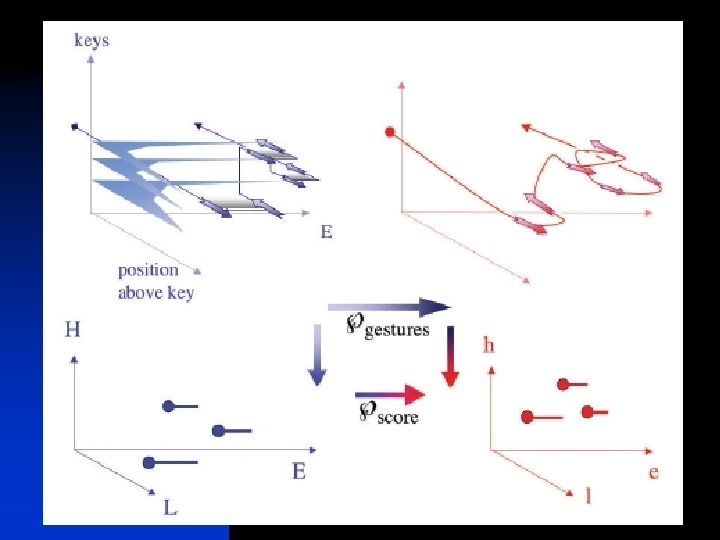
Homotopy Theory Equations or formulas (category of spectroides) Diagrams of schemes (directed graphs category) Gestures (category of diagrams of curves in topological spaces)

Formulas Music Gestures Mathematics Alexander Grothendieck: „This is probably the mathematics of the new era“

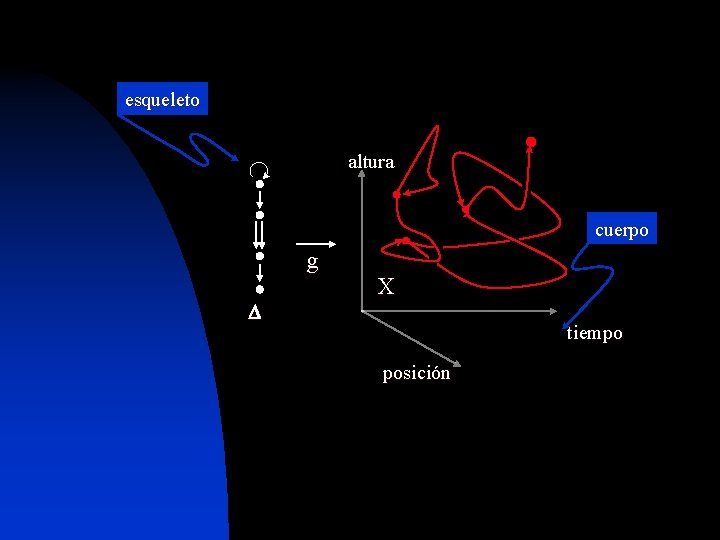
Mathematically, a gesture is defined as a digraph D, called the skeleton of the gesture together with a transformation g that associates to each arrow a of D a continuous curve g(a): I X Body of the gesture

esqueleto altura cuerpo g X tiempo posición

G. Mazzola y S. Müller 20012003

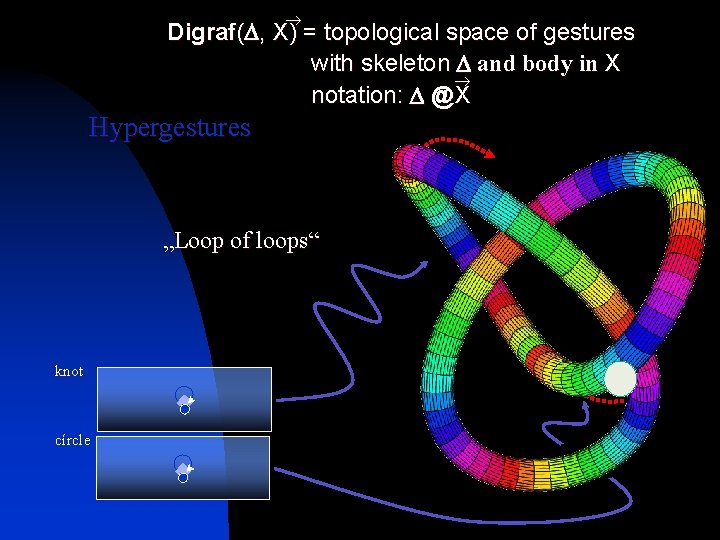
Renate Wieland “gesture within a gesture” The set of gestures of a fixed skeleton D to a topological space X is itself a topological space, denoted with D@ X. We can consider gestures h: F D@X. These gestures are called hypergestures.

Digraf( , X) = topological space of gestures with skeleton and body in X notation: @X Hypergestures „Loop of loops“ knot círcle

MCM 2017 UNAM, Mexico City.

James Joseph Sylvester (1814 -1897)

“May not Music be described as the Mathematics of sense, Mathematics as Music of the reason? The soul of each the J. J. Sylvester same? ”(1864)

Mathematics and Music n Both are “Fine Arts”. n Poseess similar characteristics. n They are related in the sense that Mathematics provides the scientific basis for understanding Music and Musicology and that the latter can be considered a science.

Mathematics is a Fine Art, the purest of them, that has the gift of being the most precise and the precisión of all Science. E. Lluis-Puebla

www. Emilio. Lluis. org lluisp@unam. mx