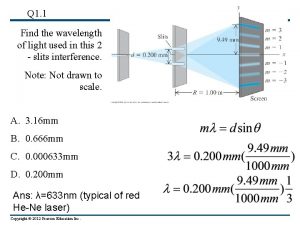
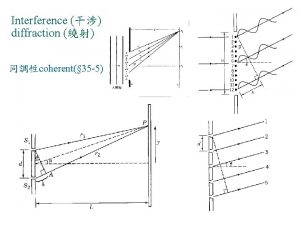
Introduction into the dynamical theory of Xray diffraction






















































































- Slides: 142

Introduction into the dynamical theory of X-ray diffraction for perfect crystals Jürgen Härtwig ESRF - The European Synchrotron CS 40220, 38043 Grenoble Cedex 9, France haertwig@esrf. fr 1

Outline 1. Introduction 2. Some results of the kinematical (geometrical) theory of X-ray diffraction 3. Dynamical theory of X-ray diffraction Short theoretical background Basic results and helpful tools (dispersion surfaces) The one “beam” case – refraction and reflection The two “beam” case 4. Some effects of dynamical X-ray diffraction Pendellösung length (Laue case), Pendellösung effect Anomalous transmission – Borrmann effect, pointing vector Bragg case and a bit X-ray optics Plane waves, monochromatic waves 2

1. Introduction What is/means “dynamical” diffraction theory? Why do we need it? Which are the differences to other, simpler theories? May I quantify if a simple theory is sufficient or not? Where is it applied? 3

Dynamical Diffraction – Applications today n X-ray topography strain and defects in (single) crystals, e. g. , dislocations, precipitates Crystal growth electronic & microelectronic development photovoltaics … n Bragg-diffracting optical elements for synchrotron radiation monochromators, phase plates (X-ray optics in general) n High resolution X-ray diffraction single crystals, epitaxial films, superlattices. . . n Grazing incidence methods (reflection, GID, GISAXS) thin films & interfaces n X-ray standing wave method (XRSW) secondary effects (photoelectrons, x-ray fluorescence etc), excited by a standing wave in a diffracting crystal n Three-beam diffraction determination of phases of the structure factors n Dynamical diffraction of light (λ ~ 1. 5 mm) in a two-dimensional or three dimensional array of holes Optical photonic crystals 4

Some history The discovery of X-ray diffraction and first theories 5

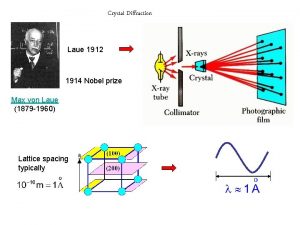
The story of X-ray diffraction and of the dynamical theory (-ies) of X-ray diffraction started with Paul Peter Ewald and Max Laue (1888 -1985) (1879 -1960) 6

It started in 1910 with … … Paul Peter Ewald’s thesis project Ewald asks Arnold Sommerfeld for a topic for a dissertation (remember – at that time it was not sure what exactly were X-rays and what a crystal) Proposal: Find out whether a lattice-like (3 D) anisotropic arrangement of isotropic resonators might be capable of exhibiting light-optical birefringence (double refraction) Result: A theory that relates macroscopic properties of light dispersion and refraction in a crystal to the interaction of propagating waves with a microscopic distribution of resonators This was already a dynamical theory, only that is was formulated for visible light 7

January 1912 Ewald wanted to discuss his results with Max Laue During the presentation of his subject he mentioned: “ … 3 -dimensional lattice …” ? ? !!! Laue 8

Laue: What are the distances between the lattice points ? Ewald: Maybe about one thousandth of the wavelength of light! Max Laue got the crucial idea: If crystals were indeed constructed like 3 -D-lattices (with distances mentioned by Ewald), and if X-rays had the properties of waves (with distances estimated by Arnold Sommerfeld, ~0. 6 nm) then X-rays should be diffracted when passing a crystal!!! 9

around Easter 1912: Experiment by W. Friedrich, P. Knipping & M. Laue Friedrich’s and Knipping’s set-up to check Laue’s idea M. Laue, W. Friedrich, P. Knipping Sitzungsberichte der Königlich Bayerischen Akademie der Wissenschaften, June 1912, M. Laue, W. Friedrich, P. Knipping, Annalen der Physik (Leipzig), 41 971 (1913) 10

One of the first exposures, taken with a Cu. S crystal plate The famous exposure “Fig. 5”, adjusted Zn. S crystal. (Friedrich et al. 1912) (Deutsches Museum, München) 11

1. X-rays are waves! 2. Crystals have a discrete, 3 -D-periodic (lattice) structure! Nobel prize 1914 for Max von Laue "For his discovery of the diffraction of X-rays by crystals" “Laue technique” Crystal orientation (SR) Structure analysis (oscillation method) X-ray topography (white beam topography, Lang topography) 12

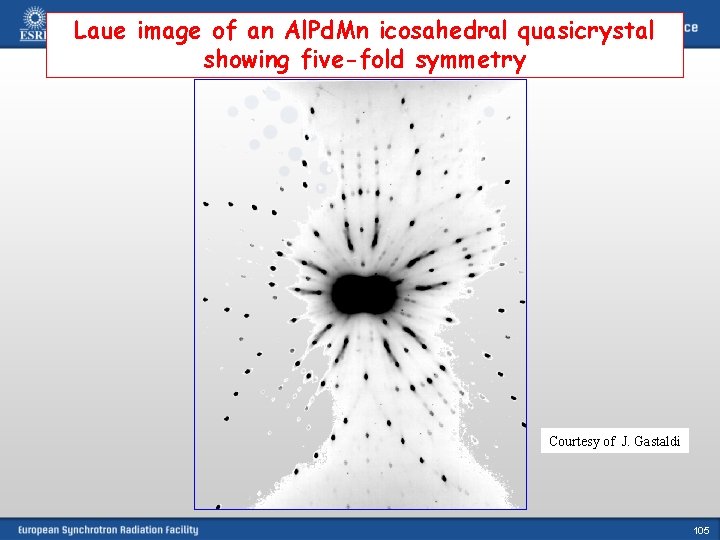
Nowadays: Laue image of an Al. Pd. Mn icosahedral quasicrystal showing five-fold symmetry “Laue spots” (position, intensity) information about crystal symmetry In general white beam used, sample position fixed Integrated intensity recorded 13

~ 40 cm ID 19 18 cm Typical Laue pattern from a small silicon sample. Δω=0° and λ=“infinite” (white beam). Typical “Laue pattern” from a tetragonal HEW lysozyme. Δω=1° and λ=0. 8Å, Δλ/λ~10 -4. Higher harmonics “contamination” for white beam λ/n = d(hkl)/n · sin θ(hkl) 14

First X-ray diffraction theories promptly followed the discovery of X-ray diffraction: 1912/13 1914 Laue’s geometrical (or kinematical) theory, Laue equations Bragg’s law 1916/17… Diffraction by a 3 D-lattice (crystal) a (sina - sina 0) = h b (sinb - sinb 0) = k c (sin - sin 0) = l Laue equations h, k, l – “Miller” (Laue) indices 15

William Lawrence Bragg (son, left) and Sir William Henry Bragg (father, right) (Courtesy Edgar Fahs Smith Memorial Collection, Department of Special Collections, University of Pennsylvania Library. ) Nobel Prize in Physics 1915: "For their services in the analysis of crystal structure by means of X-rays" 16

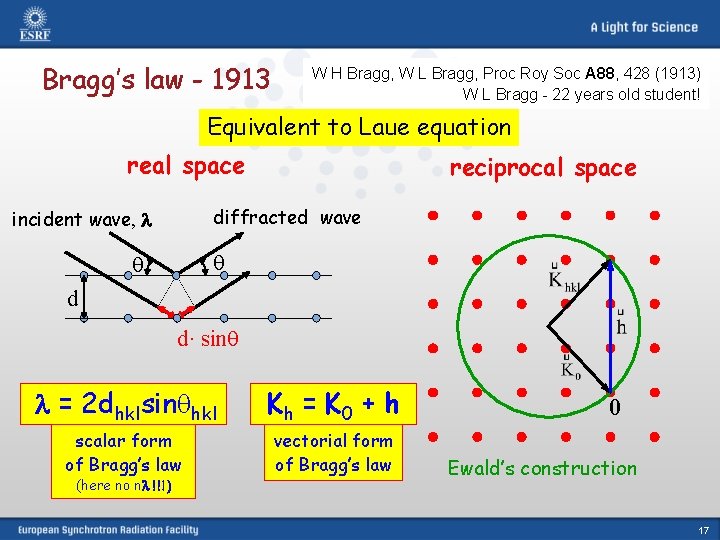
Bragg’s law - 1913 W H Bragg, W L Bragg, Proc Roy Soc A 88, 428 (1913) W L Bragg - 22 years old student! Equivalent to Laue equation real space reciprocal space diffracted wave incident wave, l d d· sin l = 2 dhklsin hkl Kh = K 0 + h scalar form of Bragg’s law vectorial form of Bragg’s law (here no nl !!!) 0 Ewald’s construction 17

Determination of the first crystal structures Na. Cl (rock-salt) fcc, KCl (Sylvine) pc, Zn. S (Zincblende) fcc, Ca. F 2, (Fluorspar) fcc, Ca. CO 3 (Calcite) rhombohedral W H Bragg, W L Bragg, Proc Roy Soc A 89, 248 (1913), submitted 21 June, accepted 26 June !!! Diamond W H Bragg, W L Bragg, Nature 91, 557 (1913), submitted 28 July, publishing date 31 July Proc Roy Soc A 89, 277 (1913), submitted 30 July!!! 18

First X-ray diffraction theories promptly followed the discovery of X-ray diffraction: 1912/13 1913 Laue’s geometrical (or kinematical) theory Bragg’s law 1914 Darwin’s geometrical and dynamical theories 1916/17 Ewald’s extension of his theory to X-rays (fully dynamical theory) C. G. Darwin, The theory of X-ray reflection, Phil. Mag. 27, 315, 675 (1914) P. P. Ewald, Ann. Phys. (Leipzig) 49, 1, 117 (1916); 54, 519 (1917) (English translations exist!) all for perfect crystals! 19

2. Kinematical (geometrical) theory of X-ray diffraction Amplitude of the diffracted wave derived by: - adding the amplitude of the waves diffracted by each scatterer - by simply taking into account the optical path differences ( “geometrical”) - neglecting the interaction of the propagating waves with matter (only one scattering process, no absorption, no refraction, energy conservation law violated!!!) 20

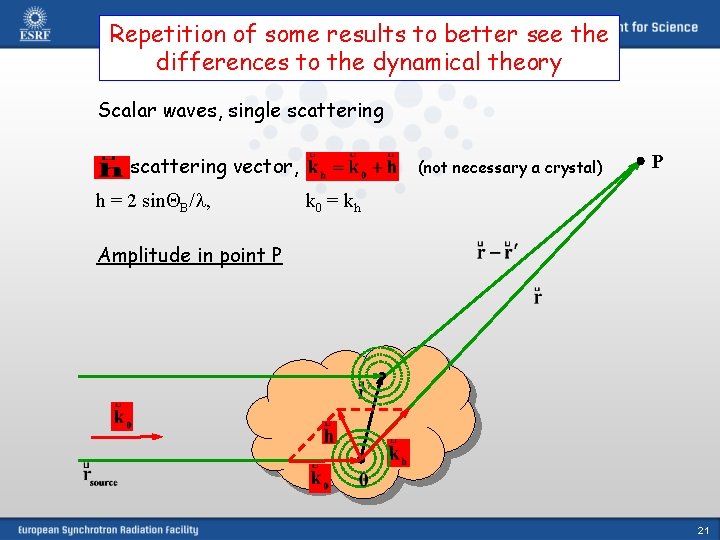
Repetition of some results to better see the differences to the dynamical theory Scalar waves, single scattering - scattering vector, h = 2 sin B/ , (not necessary a crystal) P k 0 = kh Amplitude in point P 21

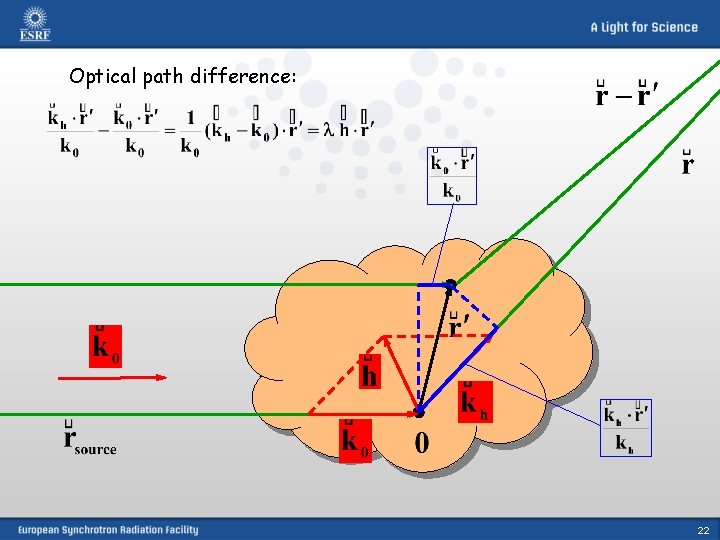
Optical path difference: 22

We use the following conditions: 1. Plane wave approximation (Fraunhofer approximation): and 2. Elastic scattering, no absorption 23

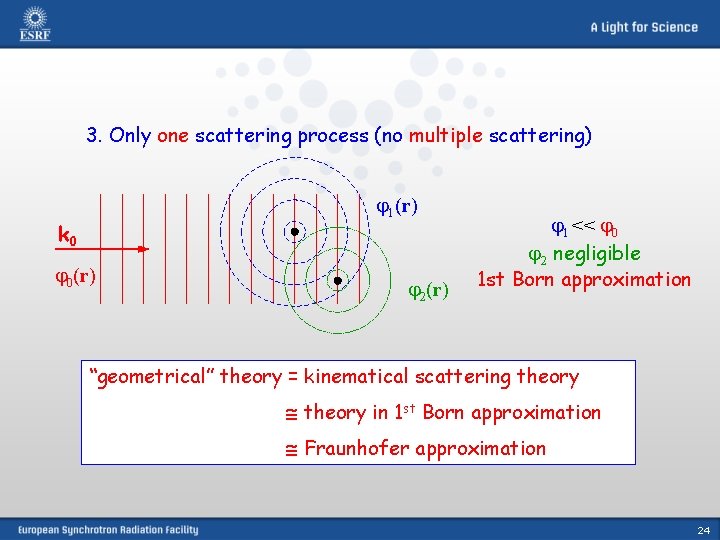
3. Only one scattering process (no multiple scattering) 1(r) k 0 0(r) 2(r) 1 << 0 2 negligible 1 st Born approximation “geometrical” theory = kinematical scattering theory in 1 st Born approximation Fraunhofer approximation 24

A little bit of theory - Amplitude in point P: (r) = 0(r) + 1(r) = 0(r) + G(r|r’) V(r’) 0(r’) d 3 r’ with: This is an approximation! Exact solution with: (r’) instead of 0(r’) - for photon scattering on electrons (re– classical electron radius, N(r) – electron density) - for thermal neutron scattering on the nuclear potential (b – scattering length) - for electron scattering on the Coulomb potential 25

Example – X-rays 0(r) – plane wave electrical field Scattered wave: Scattering amplitude: re 3· 10 -15 m 1 for s-polarization P= cos(2 B) for p-polarization factor for amplitudes Rayleigh scattering 29

Special cases: 1. Scattering on 1 electron: re 3· 10 -15 m polarization factor for intensities Thomson scattering 30

2. Scattering on 1 atom: f – atom form factor (amplitude) Remark: Fourier transform of N(r)!!! 31

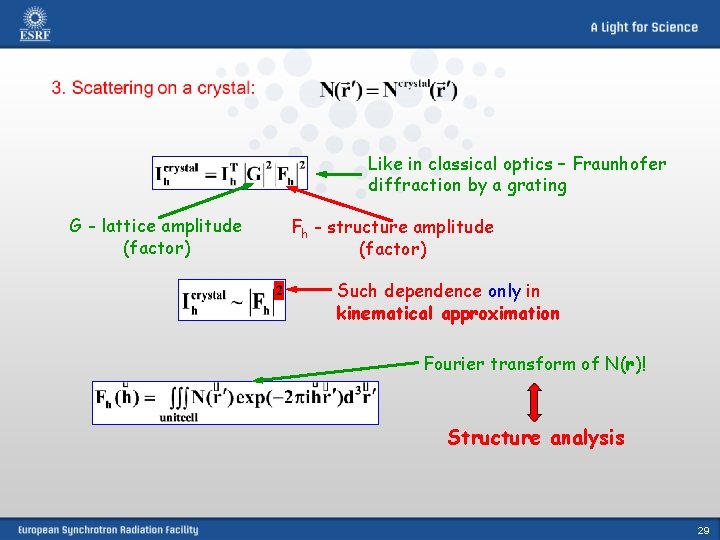
Like in classical optics – Fraunhofer diffraction by a grating G - lattice amplitude (factor) Fh - structure amplitude (factor) 2 Such dependence only in kinematical approximation Fourier transform of N(r)! Structure analysis 29

Only with these approximations: Ihcrystal ~ |Fh|2 and convenient use of: Fh FT N(r’) 30

When these approximations could be valid? Comparison with Thomson scattering: Intensity of the wave scattered by 1 electron polarization factor for intensities re – classical electron radius Estimation: re 3· 10 -15 m 1 electron, for r = 0. 1 mm Ih. T/I 0 (re/r)2 10 -21 cubic crystal: a = 0. 5 nm, Z = 30 in (1 mm)3 ~ 3· 1011 electrons single scattering OK in (1 mm)3 ~ 3· 1020 electrons single scattering? !? !? 31

Some questions: - Multiple scattering negligible for “small” crystals, but how small? What is small? - How to describe “large”, perfect (or even imperfect) crystals? (e. g. X-ray optics!!!) - What happens close to or within the crystals? (no Fraunhofer approximation) Other theory needed: dynamical theory of diffraction 32

Outline 1. Introduction 2. Some results of the kinematical (geometrical) theory of X-ray diffraction 3. Dynamical theory of X-ray diffraction Short theoretical background Basic results and helpful tools (dispersion surfaces) The one “beam” case – refraction and reflection The two “beam” case 4. Some effects of dynamical X-ray diffraction Pendellösung length (Laue case), Pendellösung effect Anomalous transmission – Borrmann effect, pointing vector Bragg case and a bit X-ray optics Plane waves, monochromatic waves 33

Some questions: - Multiple scattering negligible for “small” crystals, but how small? What is small? - How to describe “large”, perfect (or even imperfect) crystals? (e. g. X-ray optics!!!) - What happens close to or within the crystals? (no Fraunhofer approximation) Other theory needed: dynamical theory of diffraction 34

3. Dynamical theory of X-ray diffraction First dynamical X-ray diffraction theories promptly followed the discovery of X-ray diffraction: 35

Basic idea of dynamical diffraction dynamical theory means - theory including multiple scattering 1 st Born approximation n-th Born approximation with n In principle we have to change from: (r) = 0(r) + G(r|r’) V(r’) 0(r’) d 3 r’ to: (r) = 0(r) + G(r|r’) V(r’) d 3 r’

1914 Darwin’s dynamical theory C. G. Darwin, The theory of X-ray reflection, Phil. Mag. 27, 315, 675 (1914) C. G. Darwin (1887 -1962) grandson of C. Darwin 1916/17 Ewald’s extension of his theory to X-rays (fully dynamical theory) P. P. Ewald, Ann. Phys. (Leipzig) 49, 1, 117 (1916); 54, 519 (1917) Nowadays mostly used: 1931 Laue’s dynamical theory, solution of Maxwell equations in a periodic medium (crystal) in the form of Bloch-waves (wave fields) M. Von Laue, Ergeb. Exakt. Naturwiss. 10, 133 (1931) 37

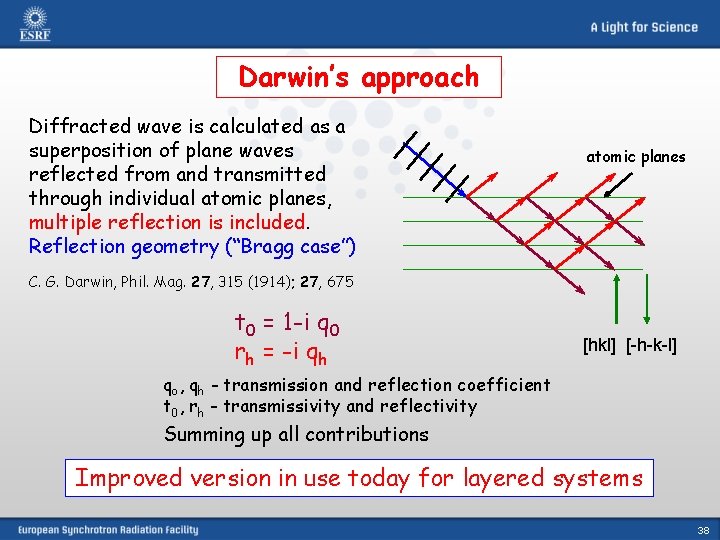
Darwin’s approach Diffracted wave is calculated as a superposition of plane waves reflected from and transmitted through individual atomic planes, multiple reflection is included. Reflection geometry (“Bragg case”) atomic planes C. G. Darwin, Phil. Mag. 27, 315 (1914); 27, 675 t 0 = 1 -i q 0 rh = -i qh [hkl] [-h-k-l] qo, qh - transmission and reflection coefficient t 0, rh - transmissivity and reflectivity Summing up all contributions Improved version in use today for layered systems 38

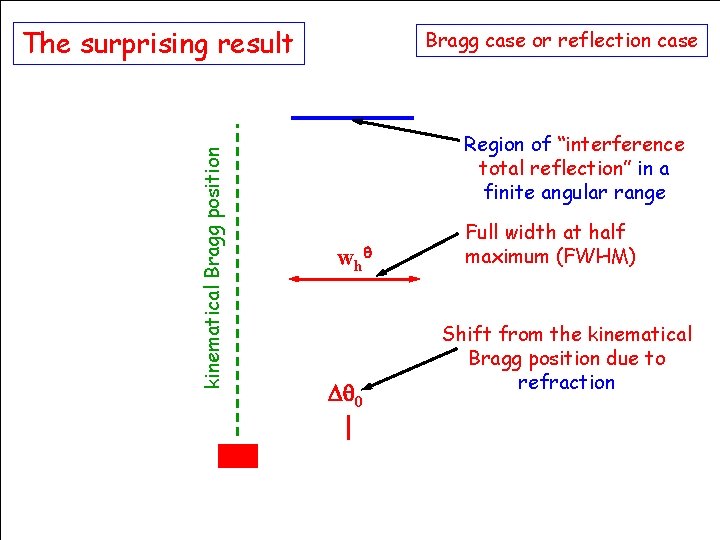
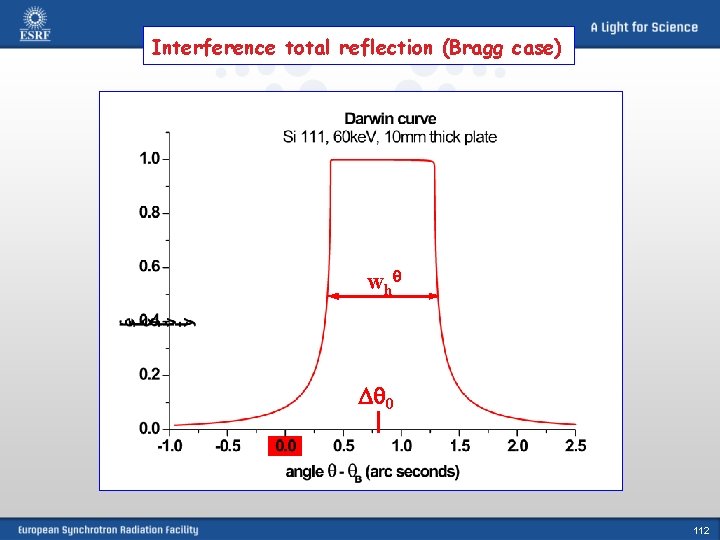
kinematical Bragg position The surprising result Bragg case or reflection case Region of “interference total reflection” in a finite angular range w h 0 Full width at half maximum (FWHM) Shift from the kinematical Bragg position due to refraction HERCULES Grenoble, March 2009 39

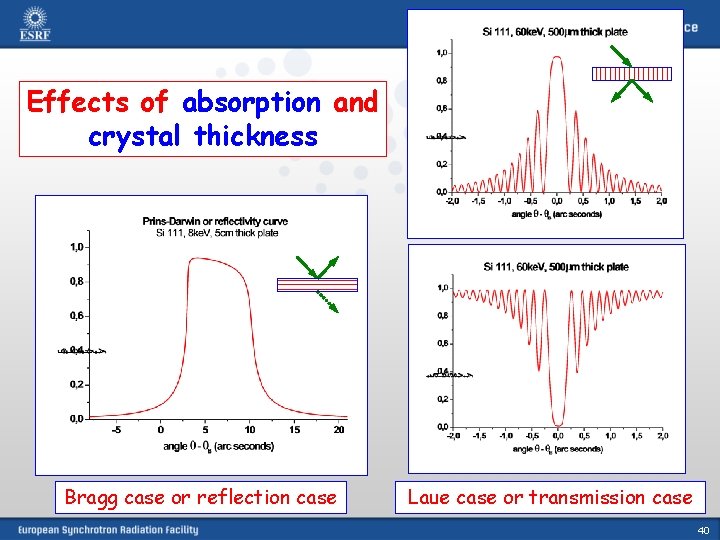
Effects of absorption and crystal thickness Bragg case or reflection case Laue case or transmission case 40

By the way … Those calculations were done with the program (program package) XOP http: //www. esrf. eu/computing/scientific/xop 2. 4/documentation. html 41

Few more typical results (and differences) of kinematical and dynamical theory Full widths at half maximum (FWHM) of reflectivity curves Kinematical theory: symmetrical Bragg case: whsym. B (dhkl/t)tan B symmetrical Laue case: Dynamical theory: (=Scherrer formula) whsym. L dhkl/t f( ) t – crystal thickness symmetrical Bragg case: whsym. B (dhkl/ 0)tan B symmetrical Laue case: whsym. L dhkl/ 0 new parameter: 0 - Pendellösung length symm. Bragg case: 0 sym. B = p VUC / (2 r 0 |P| Fhkl dhkl) f( ) symm. Laue case: 0 sym. L = p VUC / (2 r 0 |P| Fhkl dhkl tan B) 42

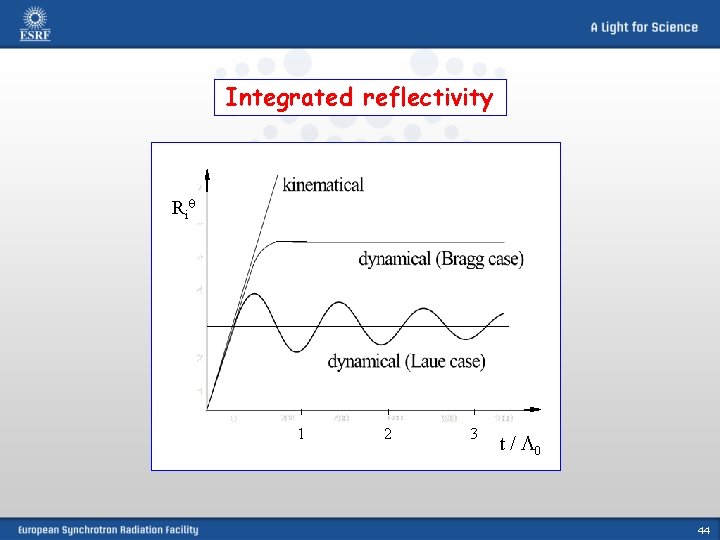
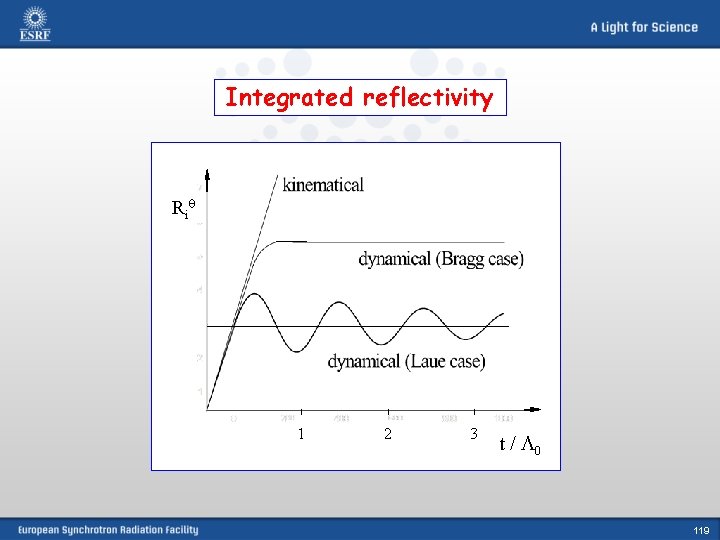
Area under reflectivity curve – integrated reflectivity No absorption, thick crystal (dynamical theory): Laue case: Bragg case: No absorption, thin crystal (kinematical limit): Both cases: V – illuminated crystal volume 43

Integrated reflectivity Ri 1 2 3 t / 0 44

In the Bragg case (thick crystal) the form and width of the reflectivity curve (as well as the integrated reflectivity) depend anymore on the crystal thickness! K 0 Kh damping with depth - extinction length (for = B + 0, centre of the reflection curve) tex = 0 / 2 p ~ micrometers Ih(z=tex) = I 0/e 45

The Pendellösung length 0 allows to define what are “small”/thin or “large”/thick crystals: with A = p t / 0 A<<1 “thin” crystal kinematical and dynamical theory are valid A>>1 “thick” crystal only dynamical theory applies 46

Which was the first direct experimental verification of the dynamical theory? ? ? Darwin’s well-known top-hat shaped reflectivity curve? ? ? Or the asymmetric (absorption!) Prins-Darwin one? ? ? 47

First published measurements of reflectivity curves: (not rocking curves!) 1962 nearly 50 years after Darwin’s results!!! 48

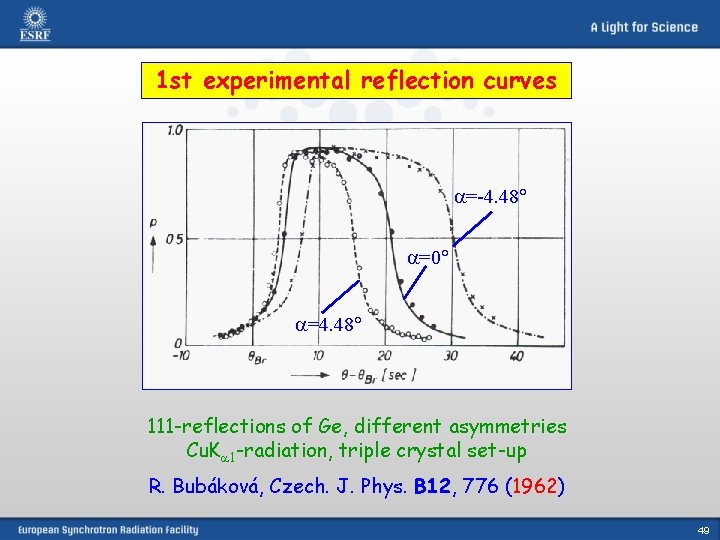
1 st experimental reflection curves a=-4. 48 a=0 a=4. 48 111 -reflections of Ge, different asymmetries Cu. Ka 1 -radiation, triple crystal set-up R. Bubáková, Czech. J. Phys. B 12, 776 (1962) 49

Why so late? Not many very good (natural) crystals available starting from the 50 ies: intensive efforts to grow high quality semiconductor crystals for the electronic industry (later also for optics and opto-electronics) No plane, monochromatic waves available – X-ray optics also solved with high quality semiconductor crystals like silicon 50

large silicon ingots dislocation free 51

Giant Crystals of Gypsum Naica mine (Chihuahua, Mexico) giant, faceted, and transparent single crystals of gypsum (Ca. SO 4· 2 H 2 O) as long as 11 m. Prof. Garcia Ruiz, Universidad de Granada, Spain Photos by Javier Trueba and Paolo Petrignani, La Venta & S/F Archives, et al. 52

First direct experimental evidence of a dynamical theory related effect anomalous transmission of X-rays through a thick crystal “Borrmann effect” discovered in 1941 G. Borrmann, Physikalische Zeitschrift 9/10, 157 -162 (1941) theoretical interpretation: M. von Laue 1949 with the (his) existing dynamical theory 53

Short theoretical background Many excellent theoreticions participated in the development and completion of the dynamical theory of X-rays diffraction P. P. Ewald C. G. Darwin M. von Laue W. H. Zachariasen Variants for: P. James “conventional” and “extended” theory A. Authier perfect crystals; plane wave, spherical wave approaches A. R. Lang deformed crystals; geometric and wave optical (even QFT) approaches Layered systems Two- and many beam cases B. W. Batterman G. Borrmann U. Bonse P. Penning & D. Polder N. Kato S. Takagi D. Taupin M. Kuriyama. . . 54

As already mentioned, in principle we have to solve: (r) = 0(r) + G(r|r’) V(r’) d 3 r’ solution of the homogeneous equ. inhomogeneity of the equation special solution of the inh. equ. But this is nothing else as the integral representation of a solution of an equation of the type: inhomogeneous wave equation 55

We shall not start with the integral representation, but from the differential equation itself and use the special property of our samples: Periodicity To describe the propagation of the waves outside and inside the crystal we use: Schrödinger equation Maxwell equations

Time free Schrödinger and monochromatic wave equations: or and or with K=1/ , -vacuum wave length using rot = grad div - and div. E = 0 we obtain one type of equation for both cases: The same type of equation for X-rays, electrons, neutrons, ions, atoms, etc. !

For a crystal V(r), VFermi(r), N(r), e(r), UC(r) are periodic in 3 -D!!! We look for solutions in the form of Bloch waves. for the electrical field vector: where is triply periodic k 0 – wave number in the crystal This allows to use Fourier expansions for the solution of the differential equation 58

For the electrical susceptibility: ε = (1+xe) ε 0 For the triply periodic amplitude of the electrical field vector: we obtain: Here holds for the wave vectors within the crystal This does not imply that holds for the vacuum!!!! Two equivalent images: 1. “plane” wave with a modulated (3 -D) amplitude (Bloch w. ) 2. Wave field consisting of h plane waves with different wave vectors kh 59

Fourier component of the electrical susceptibility is directly related to the structure factor with r 0 – classical electron radius and VUC – unit cell volume 60

Schematic way of solution inhomogeneous differential equation put Fourier expansions of all 3 -D-periodic functions into it basic equation of dynamical theory homogeneous system of algebraic equations of the order h condition for non-trivial solutions dispersion relation all possible solutions for the infinite crystal boundary conditions for wave vectors and amplitudes realised solutions for the finite crystal 61

Outline 1. Introduction 2. Some results of the kinematical (geometrical) theory of X-ray diffraction 3. Dynamical theory of X-ray diffraction Short theoretical background Basic results and helpful tools (dispersion surfaces) The one “beam” case – refraction and reflection The two “beam” case 4. Some effects of dynamical X-ray diffraction Pendellösung length (Laue case), Pendellösung effect Anomalous transmission – Borrmann effect, pointing vector Bragg case and a bit X-ray optics Plane waves, monochromatic waves 62

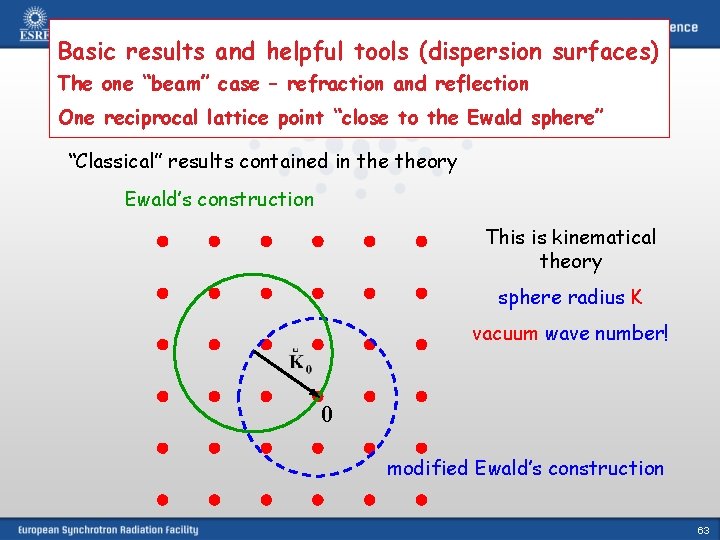
Basic results and helpful tools (dispersion surfaces) The one “beam” case – refraction and reflection One reciprocal lattice point “close to the Ewald sphere” “Classical” results contained in theory Ewald’s construction This is kinematical theory sphere radius K vacuum wave number! 0 modified Ewald’s construction 63

But the crystal is matter with nmatter nvacuum The theory provides Basic equation: (K 2 – k 02) E 0 + K 2 0 e E 0 = 0 Dispersion equation: K 2 (1+ 0 e) – k 02 = k 2 - k 02 = 0 0 mean wave number in the crystal complex value - absorption dispersion surface for the one beam case 15 ke. V, Si n = 1 – 2. 2 10 -6 –i 1. 5 10 -8 64

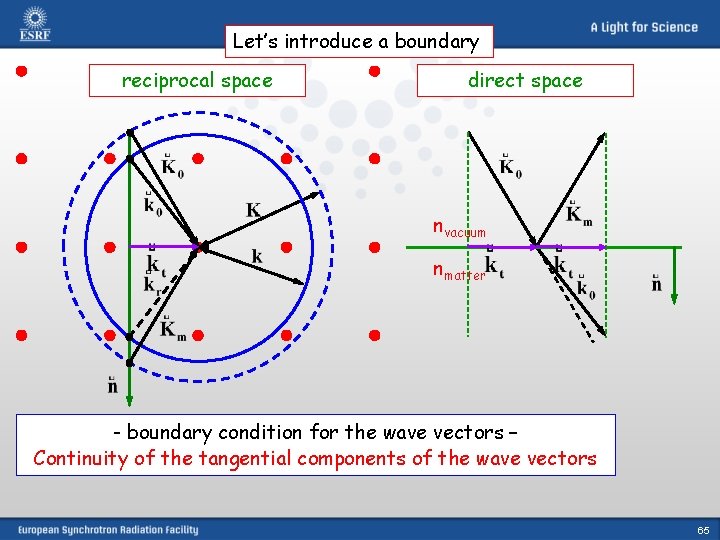
Let’s introduce a boundary reciprocal space direct space nvacuum nmatter - boundary condition for the wave vectors – Continuity of the tangential components of the wave vectors 65

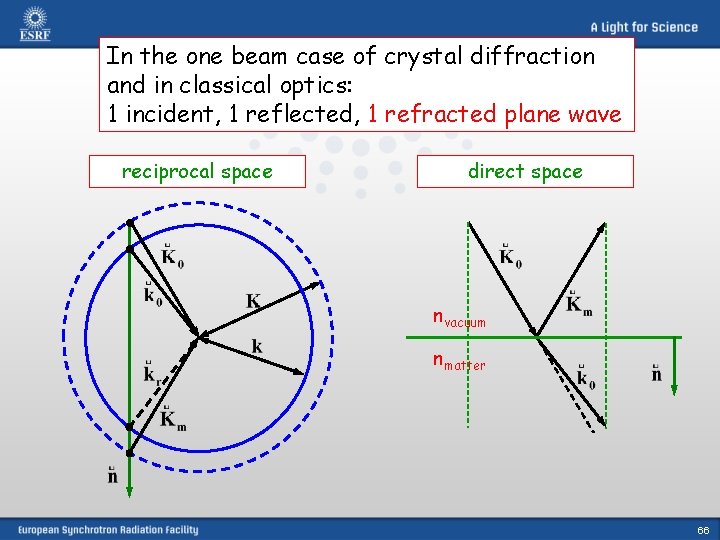
In the one beam case of crystal diffraction and in classical optics: 1 incident, 1 reflected, 1 refracted plane wave reciprocal space direct space nvacuum nmatter 66

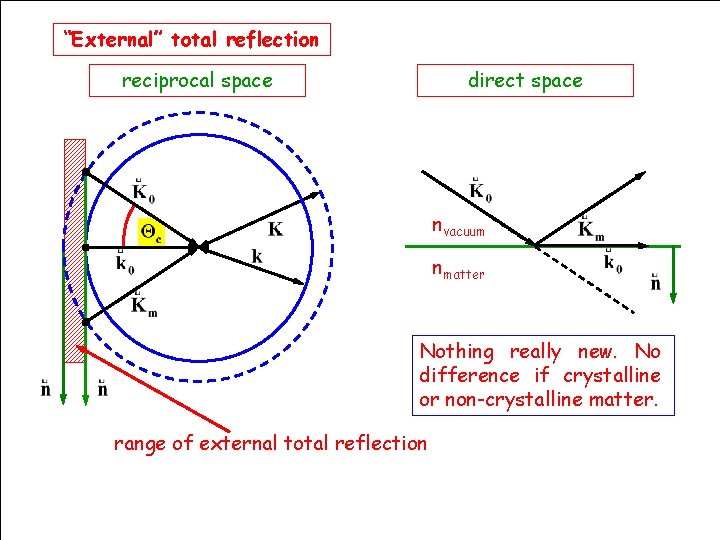
“External” total reflection reciprocal space direct space nvacuum nmatter Nothing really new. No difference if crystalline or non-crystalline matter. range of external total reflection HERCULES Grenoble, March 2009 67

The two “beam” case Two reciprocal lattice points close to the Ewald sphere The theory provides Basic equations: (k 2 – k 02) E 0 + K 2 P -he Eh = 0 K 2 P he E 0 + (k 2 – kh 2) Eh = 0 Dispersion equation: (k 2 – k 02) (k 2 - kh 2) = K 4 P 2 he -he 0 Remarks and conclusions: 1. Known problem - electron in periodic potential (e. g. Kittel) 2. It never holds that k 02 = k 2, kh 2 = k 2, k 02 = K 2, kh 2 = K 2. The endpoints of vectors k 0 and kh are never ON the Ewald sphere, nor on the sphere with diameter k. 3. The dispersion relation provides “sets” of 4 solutions, but an infinite number of them (direction of k 0 is free – boundary condition necessary for selection) 4. Polarisation - two independent solution sets for P=1 and P=cos 2 B 68

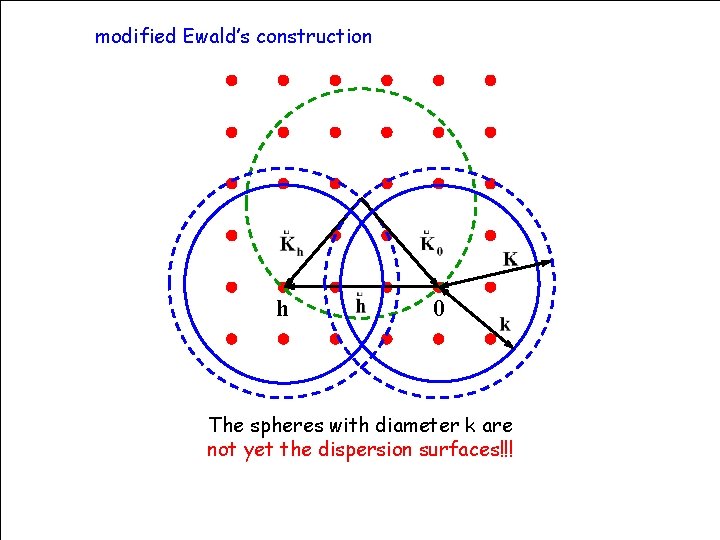
modified Ewald’s construction h 0 The spheres with diameter k are not yet the dispersion surfaces!!! HERCULES Grenoble, March 2009 69

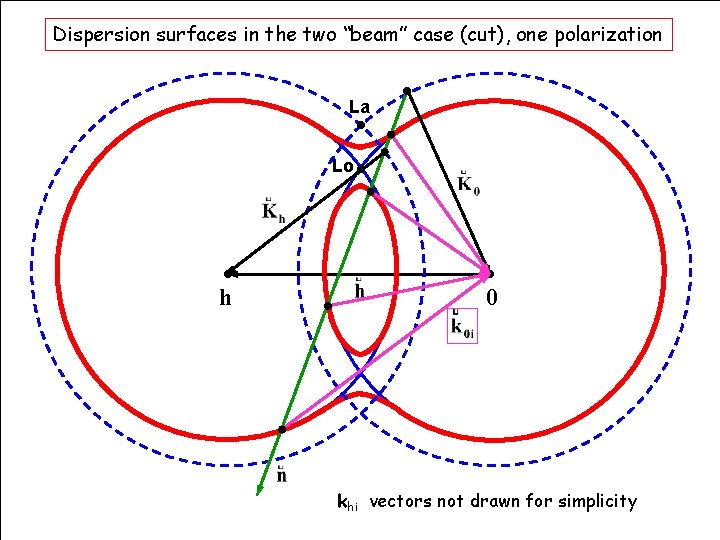
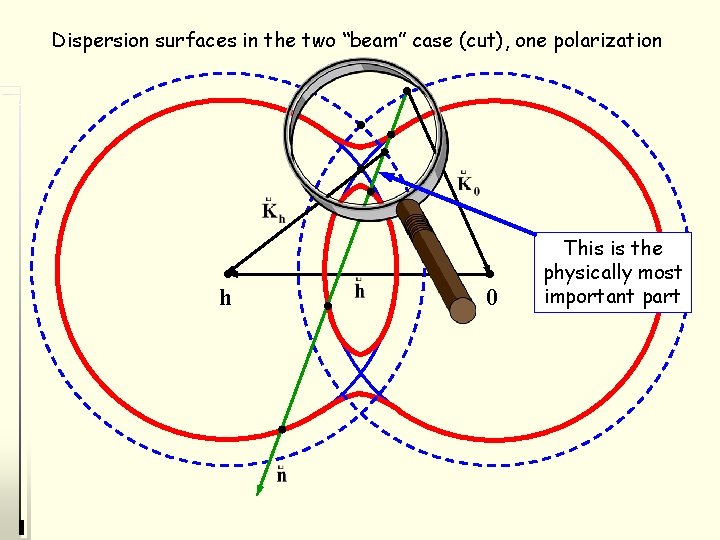
Dispersion surfaces in the two “beam” case (cut), one polarization La Lo h 0 khi vectors not drawn for simplicity HERCULES Grenoble, March 2009 70

One wave vector K 0 and the boundary condition for the wave vectors (related surface normal n) selects one “set” of 4 solutions (for one polarization state) Dispersion equation – 4 th order equation: (k 2 – k 02) (k 2 - kh 2) = K 4 P 2 he -he 0 4 wave fields (consisting of two plane waves each) may be excited the related wave vectors start at the 4 “tie points” (intersection point of the dispersion surface with the surface normal) “Extended” dynamical theory, needed in techniques/cases like: K 0, or Kh, or both with “small” angle to surface (~ Θc, strongly asymmetric cases), GID, SAXRD “Extended” dynamical theory is the non-approximated one! 71

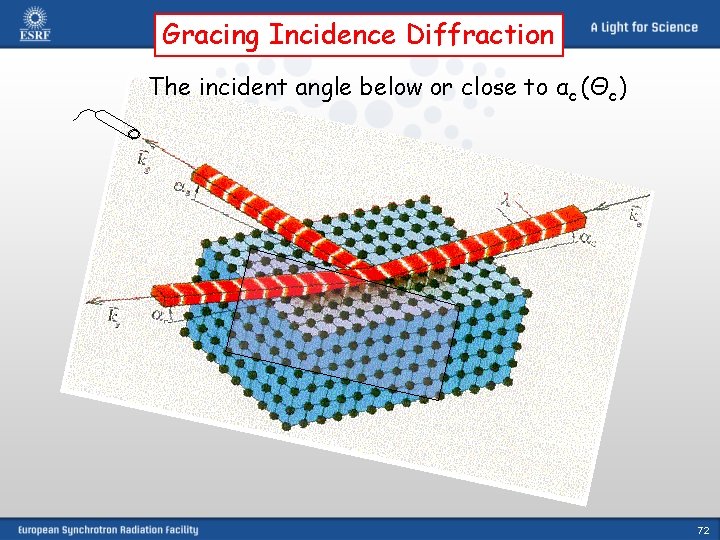
Gracing Incidence Diffraction The incident angle below or close to αc (Θc) 72

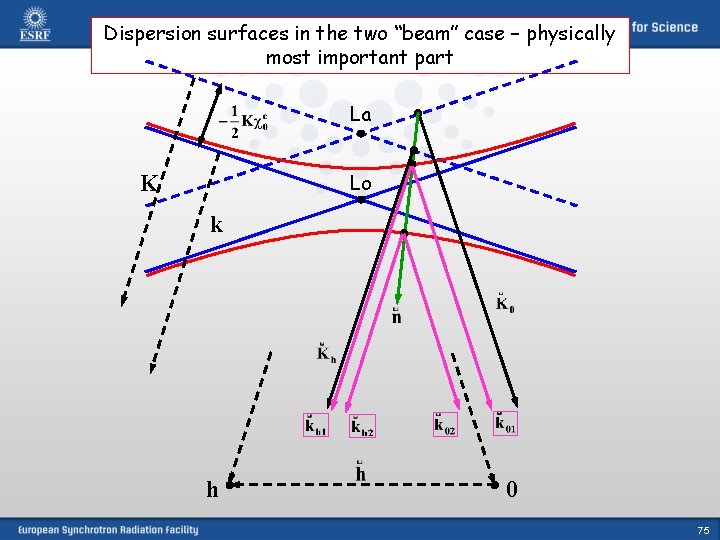
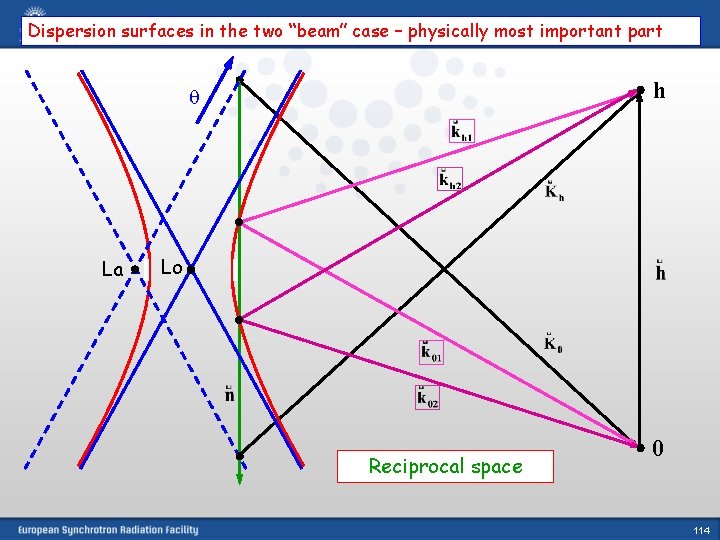
Dispersion surfaces in the two “beam” case (cut), one polarization h 0 This is the physically most important part

One wave vector K 0 and the related surface normal n selects one “set” of 4 solutions (for one polarization state), but only two may be of physical importance 2 wave fields (consisting of two plane waves each) out of the 4 excited ones are considered the related wave vectors start at the 2 “tie points”, close to the Laue- and Lorentz points In this approximation: dispersion equation – 2 nd order equation: (k – k 0) (k - kh) = ¼K 2 P 2 he -he 0 “Conventional” dynamical theory (this is an approximation!!!) 74

Dispersion surfaces in the two “beam” case – physically most important part La Lo K k h 0 75

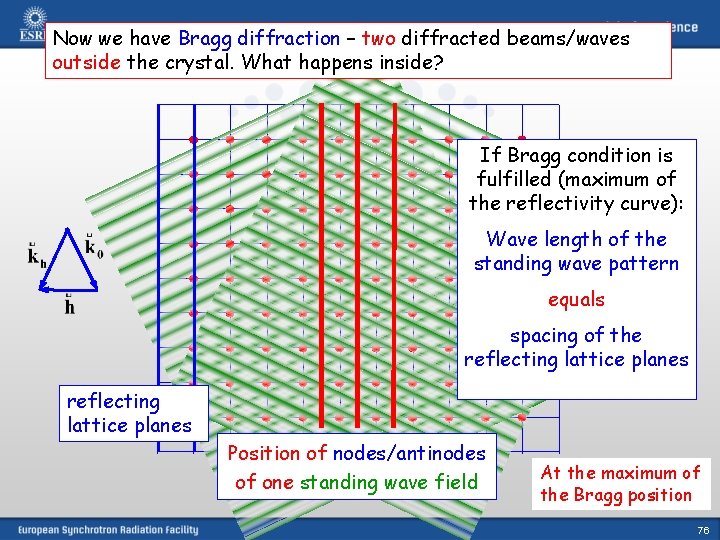
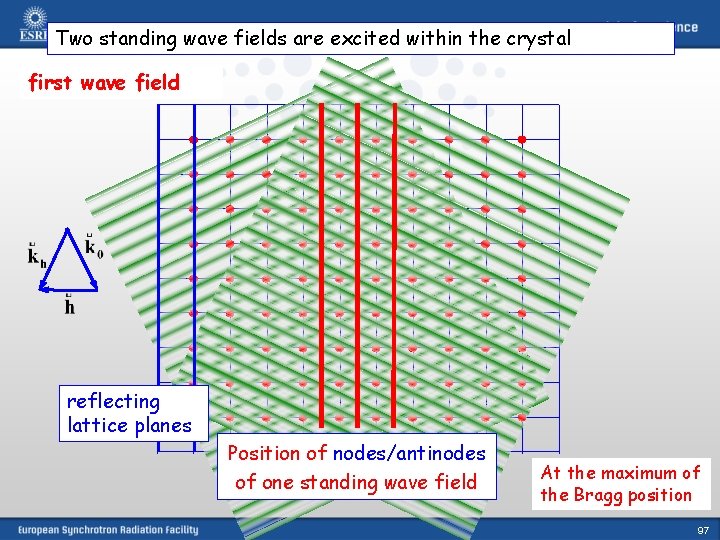
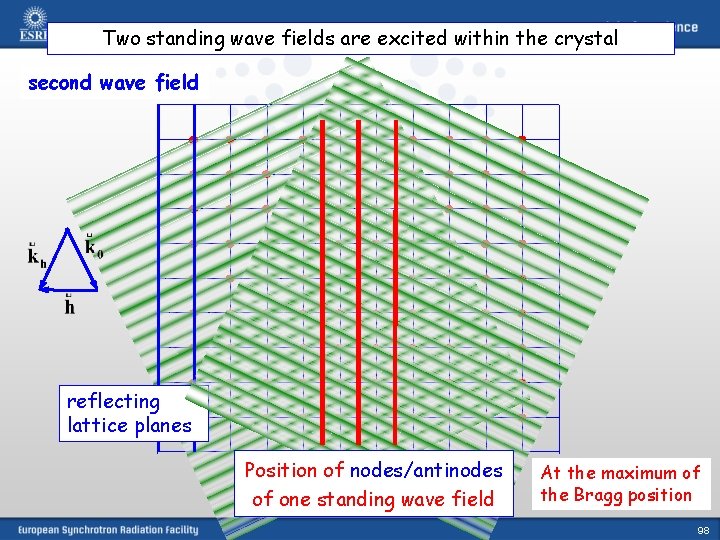
Now we have Bragg diffraction – two diffracted beams/waves outside the crystal. What happens inside? If Bragg condition is fulfilled (maximum of the reflectivity curve): Wave length of the standing wave pattern equals spacing of the reflecting lattice planes Position of nodes/antinodes of one standing wave field At the maximum of the Bragg position 76

The dynamical effects are related to the existence of coherent wave fields in the crystal and are due to different interferences between their plane wave components 77

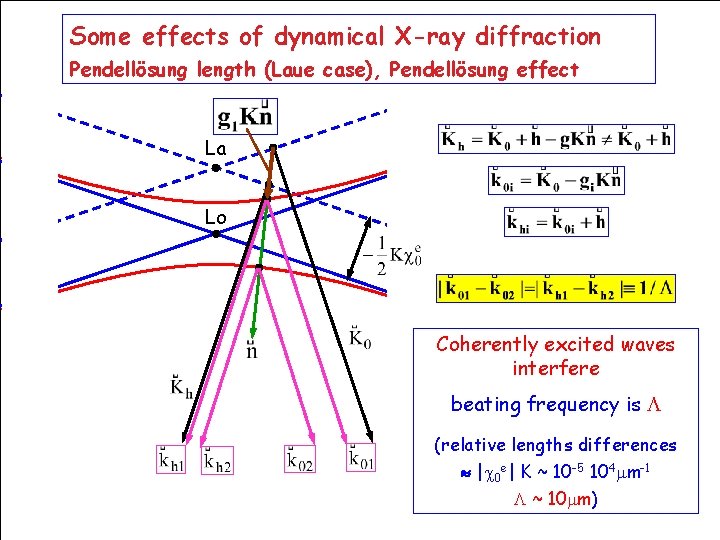
Some effects of dynamical X-ray diffraction Pendellösung length (Laue case), Pendellösung effect La Lo Coherently excited waves interfere beating frequency is (relative lengths differences | 0 e| K ~ 10 -5 104 mm-1 ~ 10 mm) HERCULES Grenoble, March 2009 78

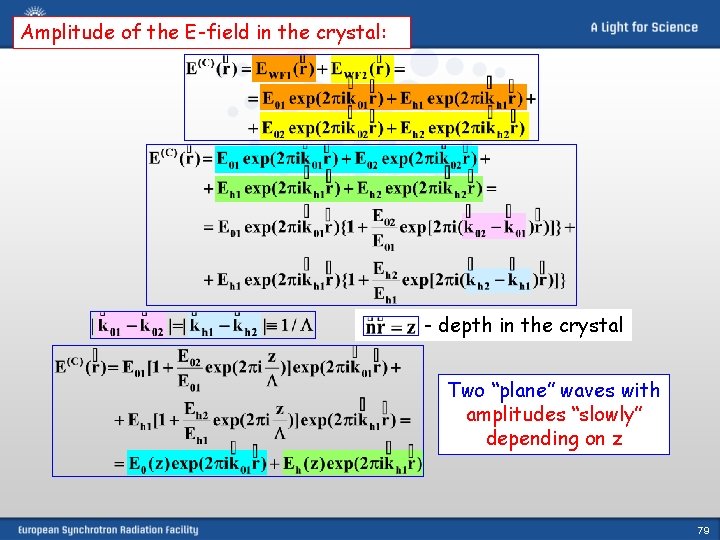
Amplitude of the E-field in the crystal: - depth in the crystal Two “plane” waves with amplitudes “slowly” depending on z 79

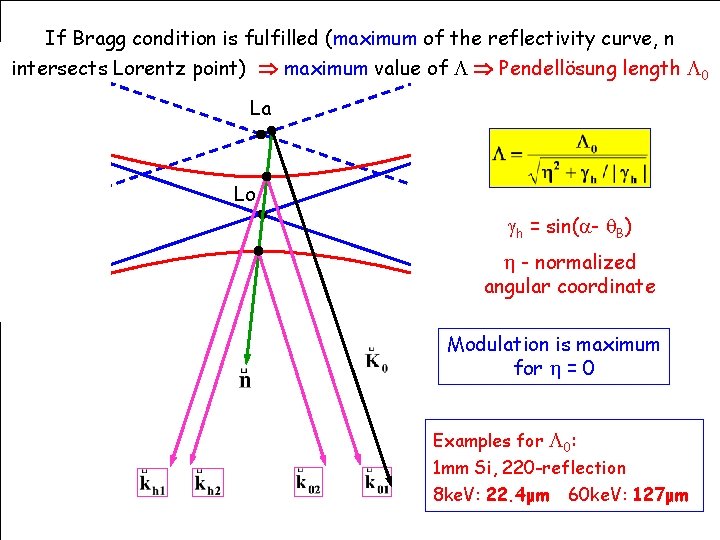
If Bragg condition is fulfilled (maximum of the reflectivity curve, n intersects Lorentz point) maximum value of Pendellösung length 0 La Lo h = sin(a- B) - normalized angular coordinate Modulation is maximum for = 0 Examples for 0: 1 mm Si, 220 -reflection 8 ke. V: 22. 4μm 60 ke. V: 127μm HERCULES Grenoble, March 2009 80

Pendellösung effect Boundary condition for amplitudes at the entrance surface: = 0, no absorption At the surface z = 0 Amplitude of wave E 0: and of wave Eh: In depth z = 0/2 In depth z = 0 etc. E 0(z=0) = E 0 Eh(z=0) = 0 E 0(z= 0/2) = 0 Eh(z= 0/2) = E 0(z= 0) = E 0 Eh(z= 0) = 0 81

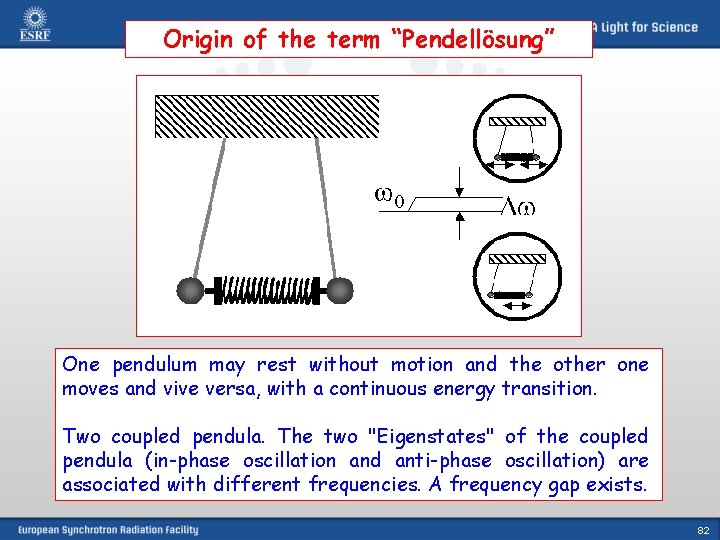
Origin of the term “Pendellösung” One pendulum may rest without motion and the other one moves and vive versa, with a continuous energy transition. Two coupled pendula. The two "Eigenstates" of the coupled pendula (in-phase oscillation and anti-phase oscillation) are associated with different frequencies. A frequency gap exists. 82

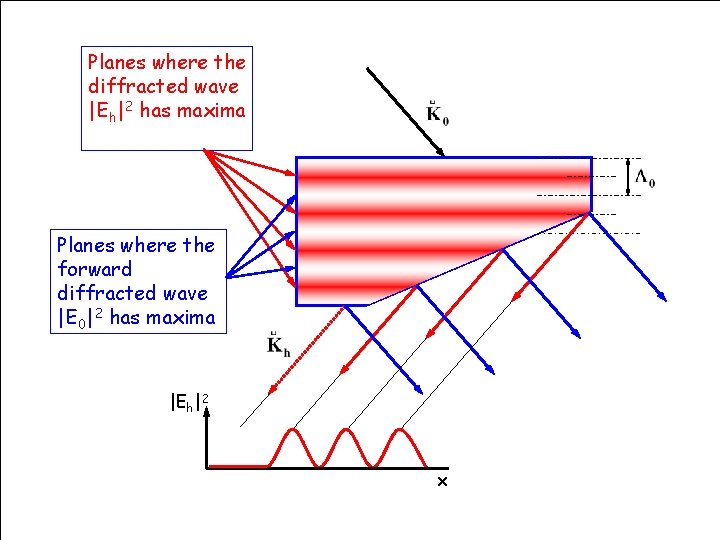
Planes where the diffracted wave |Eh|2 has maxima Planes where the forward diffracted wave |E 0|2 has maxima |Eh|2 x HERCULES Grenoble, March 2009 83

Experimental example – Pendellösung fringes in X-ray diffraction topography ~ equal thickness fringes in optics 500 mm Double crystal X-ray diffraction topograph of a silicon sample with wedge-shaped borders. (crystal: 100 orientation, t 450 mm, asymmertrical 111 -reflection in transmission; monochromator: symmetrical 111 -reflection; energy E=30 ke. V; 0 46 mm 84

Defect images in an X-ray white beam topograph stacking fault strain field of inclusion dislocations Highly pure HPHT type IIa 100 -oriented diamond (Element Six SA) 4 mm “Perfect” parts: Homogeneous local intensity/grey level equal thickness fringes surface scratch transmission geometry 85

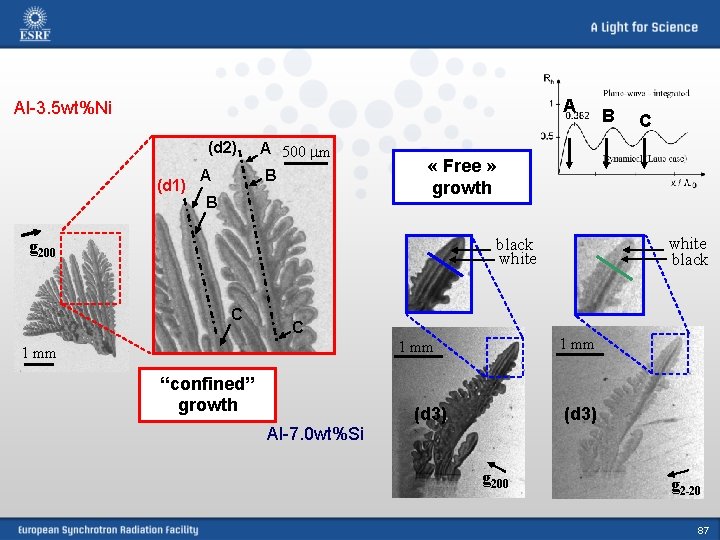
Possible applications: - measurements of structure factors (thickness known) symm. Laue case: 0 sym. L = p VUC / (2 r 0 |P| Fhkl dhkl tan B) - thickness measurements for “inaccessible” objects (e. g. growing dendrites in a crucible) 86

A Al-3. 5 wt%Ni (d 2) (d 1) A A 500 mm B B white black white C 1 mm “confined” growth C « Free » growth g 200 C B (d 3) Al-7. 0 wt%Si g 200 g 2 -20 87

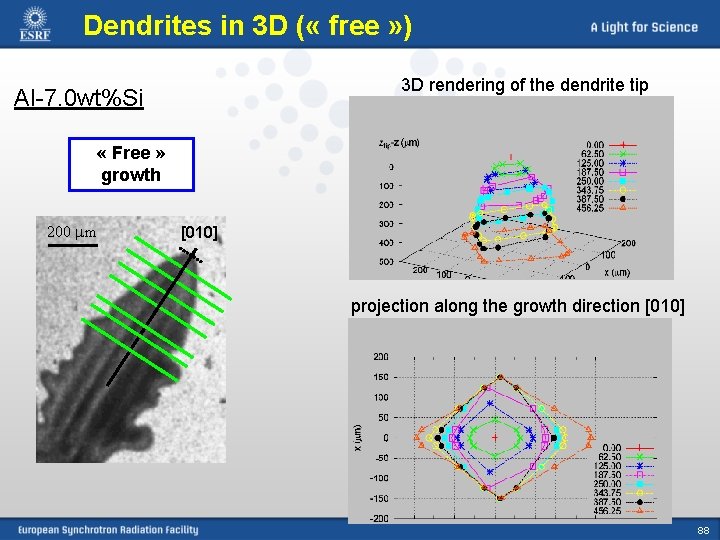
Dendrites in 3 D ( « free » ) 3 D rendering of the dendrite tip Al-7. 0 wt%Si « Free » growth 200 mm [010] 200 um projection along the growth direction [010] 88

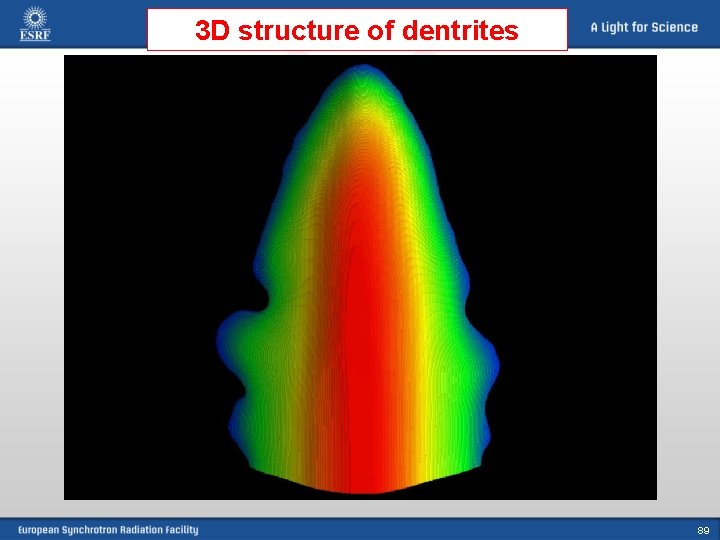
3 D structure of dentrites 89

Short break for discussion

Outline 1. Introduction 2. Some results of the kinematical (geometrical) theory of X-ray diffraction 3. Dynamical theory of X-ray diffraction Short theoretical background Basic results and helpful tools (dispersion surfaces) The one “beam” case – refraction and reflection The two “beam” case 4. Some effects of dynamical X-ray diffraction Pendellösung length (Laue case), Pendellösung effect Anomalous transmission – Borrmann effect, pointing vector Bragg case and a bit X-ray optics Plane waves, monochromatic waves 91

First direct experimental evidence of a dynamical theory related effect anomalous transmission of X-rays through a “thick” (strongly absorbing) crystal “Borrmann effect” discovered in 1941 G. Borrmann, Physikalische Zeitschrift 9/10, 157 -162 (1941) theoretical interpretation: M. von Laue 1949 with the existing (his) dynamical theory 92

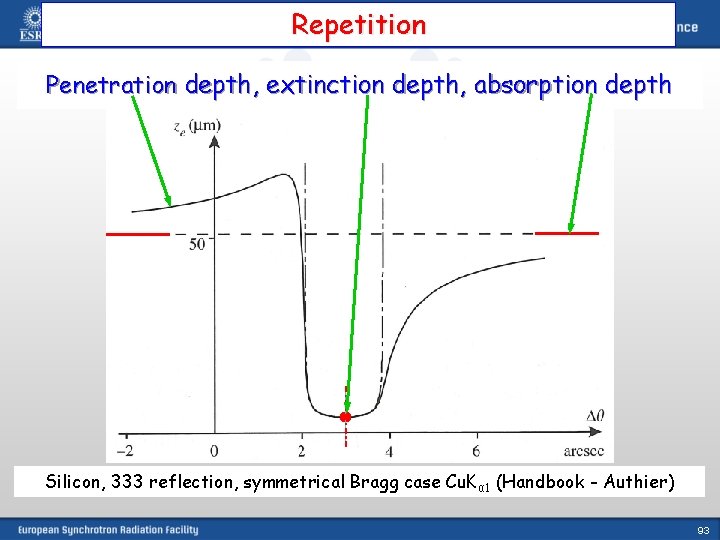
Repetition Penetration depth, extinction depth, absorption depth Silicon, 333 reflection, symmetrical Bragg case Cu. K α 1 (Handbook - Authier) 93

Anomalous transmission – Borrmann effect Observation: In Bragg condition it is possible that X-rays pass a good quality crystal for combinations of wavelength λ and crystal thickness t, where normal absorption is so high that I = I 0 exp(-μ 0 t) 0 94

Anomalous transmission – Borrmann effect Assumptions: - two beam case, coplanar diffraction - no extreme condition (extreme asymmetry, B 90º) - symmetrical Laue (transmission) case - s-polarisation Two wave fields in the crystal wave field 1 wave field 2 95

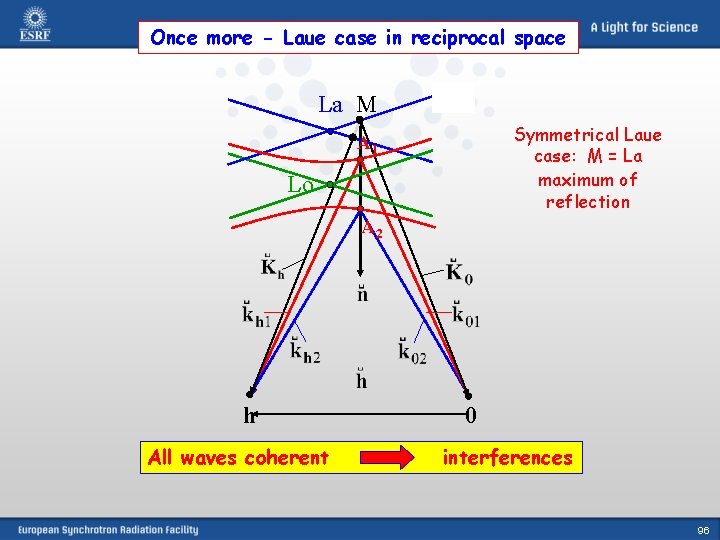
Once more - Laue case in reciprocal space La M Symmetrical Laue case: M = La maximum of reflection A 1 Lo A 2 h All waves coherent 0 interferences 96

Two standing wave fields are excited within the crystal first wave field reflecting lattice planes Position of nodes/antinodes of one standing wave field At the maximum of the Bragg position 97

Two standing wave fields are excited within the crystal second wave field reflecting lattice planes Position of nodes/antinodes of one standing wave field At the maximum of the Bragg position 98

Intensity of one wave field in the crystal For simplicity at the maximum: Ehi/E 0 i = 1 -1 WF 1; 1 WF 2 equation of lattice planes 99

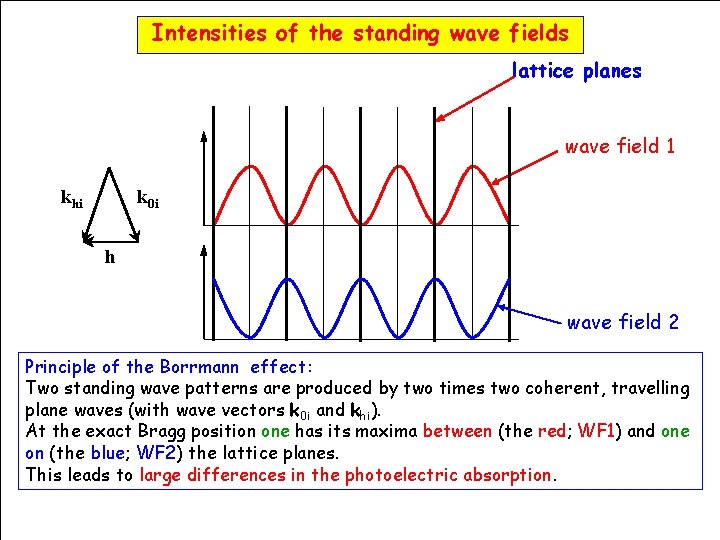
Intensities of the standing wave fields lattice planes wave field 1 k 0 i khi h wave field 2 Principle of the Borrmann effect: Two standing wave patterns are produced by two times two coherent, travelling plane waves (with wave vectors k 0 i and khi). At the exact Bragg position one has its maxima between (the red; WF 1) and one on (the blue; WF 2) the lattice planes. This leads to large differences in the photoelectric absorption. HERCULES Grenoble, March 2009 100

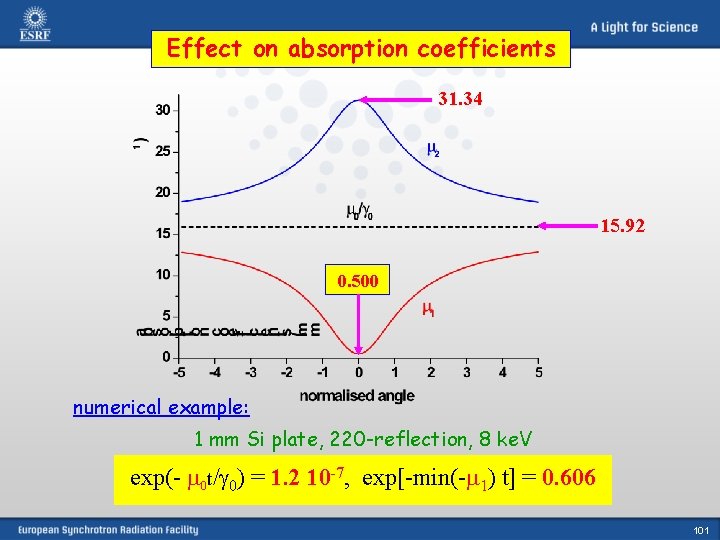
Effect on absorption coefficients 31. 34 15. 92 0. 500 numerical example: 1 mm Si plate, 220 -reflection, 8 ke. V exp(- m 0 t/ 0) = 1. 2 10 -7, exp[-min(-m 1) t] = 0. 606 101

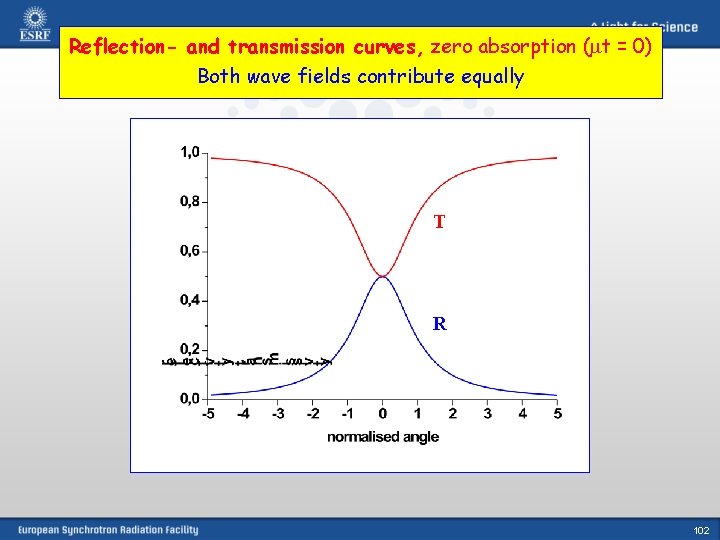
Reflection- and transmission curves, zero absorption (mt = 0) Both wave fields contribute equally T R 102

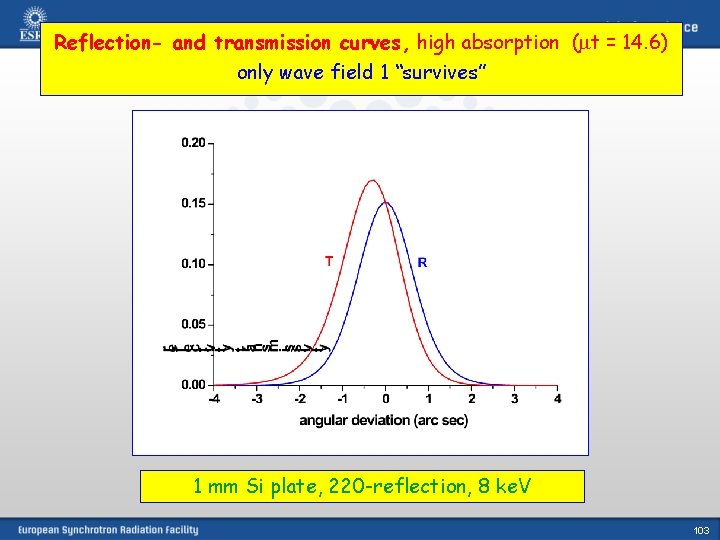
Reflection- and transmission curves, high absorption (mt = 14. 6) only wave field 1 “survives” 1 mm Si plate, 220 -reflection, 8 ke. V 103

Similar effects for other particles, e. g. ion channeling Allows to pass through rather thick samples Strongest effect for s-polarized wave may be used as polariser Very sensitive to perfection detection of defects in bulky crystals We used it to check the degree of perfection of icosahedral Al-Mn-Pd quasicrystals 104

Laue image of an Al. Pd. Mn icosahedral quasicrystal showing five-fold symmetry Courtesy of J. Gastaldi 105

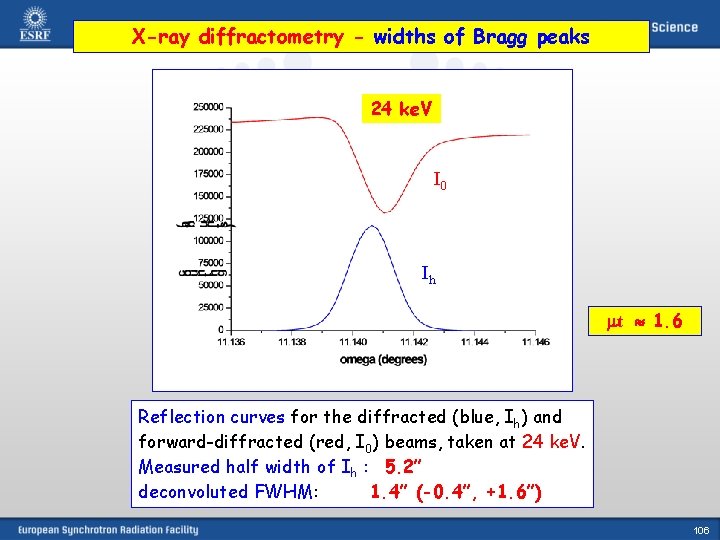
X-ray diffractometry - widths of Bragg peaks 24 ke. V I 0 Ih mt 1. 6 Reflection curves for the diffracted (blue, Ih) and forward-diffracted (red, I 0) beams, taken at 24 ke. V. Measured half width of Ih : 5. 2” deconvoluted FWHM: 1. 4” (-0. 4”, +1. 6”) 106

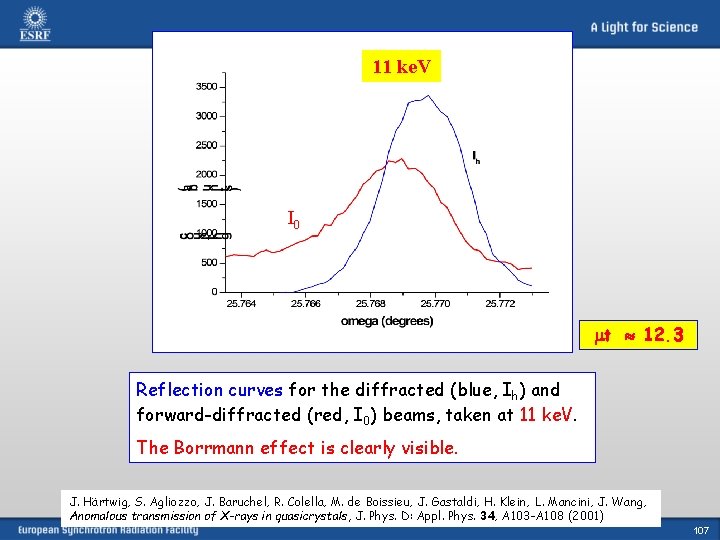
11 ke. V Ih I 0 mt 12. 3 Reflection curves for the diffracted (blue, Ih) and forward-diffracted (red, I 0) beams, taken at 11 ke. V. The Borrmann effect is clearly visible. J. Härtwig, S. Agliozzo, J. Baruchel, R. Colella, M. de Boissieu, J. Gastaldi, H. Klein, L. Mancini, J. Wang, Anomalous transmission of X-rays in quasicrystals, J. Phys. D: Appl. Phys. 34, A 103 -A 108 (2001) 107

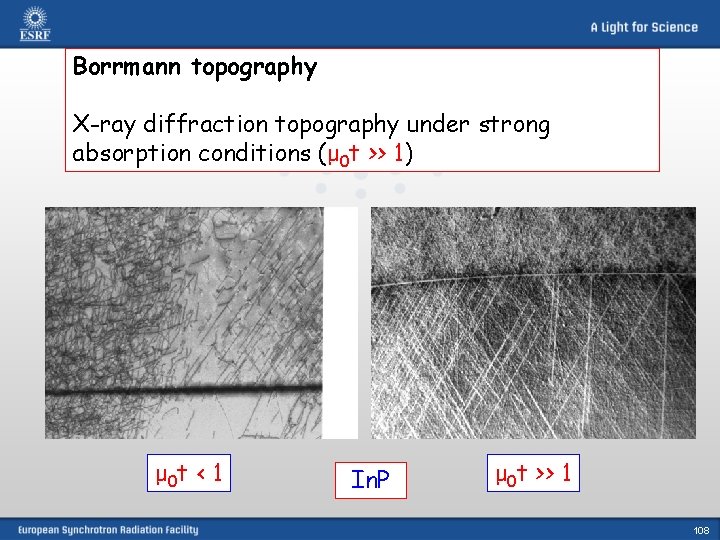
Borrmann topography X-ray diffraction topography under strong absorption conditions (μ 0 t >> 1) μ 0 t < 1 In. P μ 0 t >> 1 108

Outline 1. Introduction 2. Some results of the kinematical (geometrical) theory of X-ray diffraction 3. Dynamical theory of X-ray diffraction Short theoretical background Basic results and helpful tools (dispersion surfaces) The one “beam” case – refraction and reflection The two “beam” case 4. Some effects of dynamical X-ray diffraction Pendellösung length (Laue case), Pendellösung effect Anomalous transmission – Borrmann effect, pointing vector Bragg case and a bit X-ray optics Plane waves, monochromatic waves 109

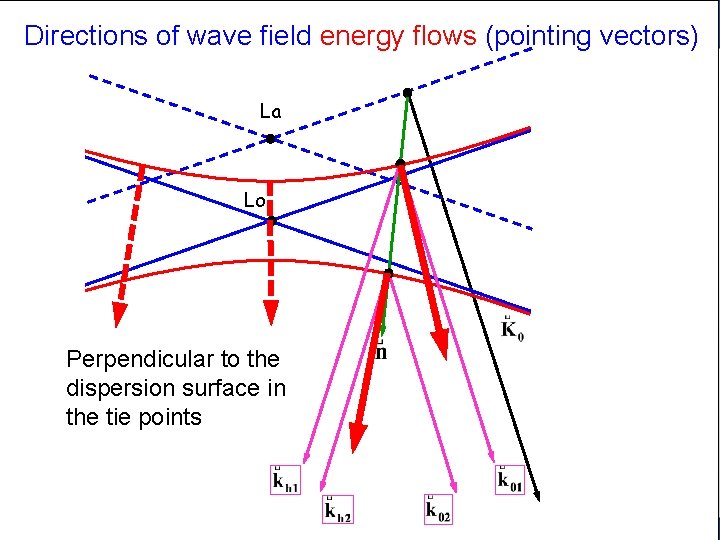
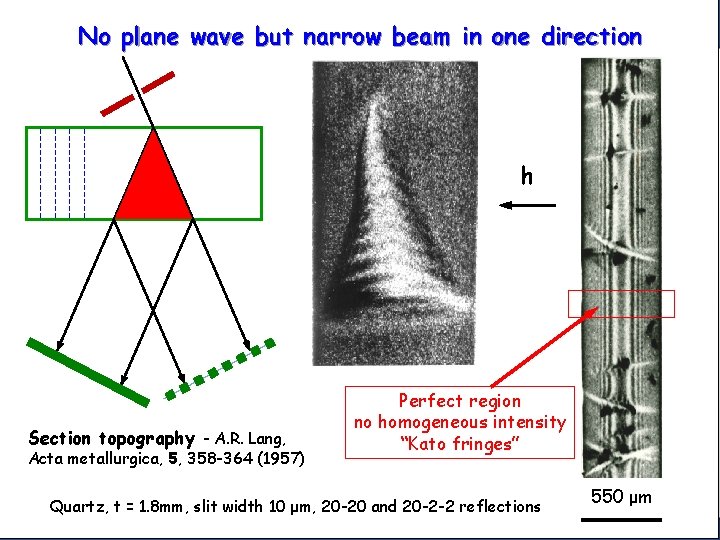
Directions of wave field energy flows (pointing vectors) La Lo Perpendicular to the dispersion surface in the tie points 110

No plane wave but narrow beam in one direction h Section topography - A. R. Lang, Acta metallurgica, 5, 358 -364 (1957) Perfect region no homogeneous intensity “Kato fringes” Quartz, t = 1. 8 mm, slit width 10 μm, 20 -20 and 20 -2 -2 reflections 550 μm 111

Interference total reflection (Bragg case) w h 0 112

Bragg case – most important case for monochromators direct space HERCULES Grenoble, March 2009 113

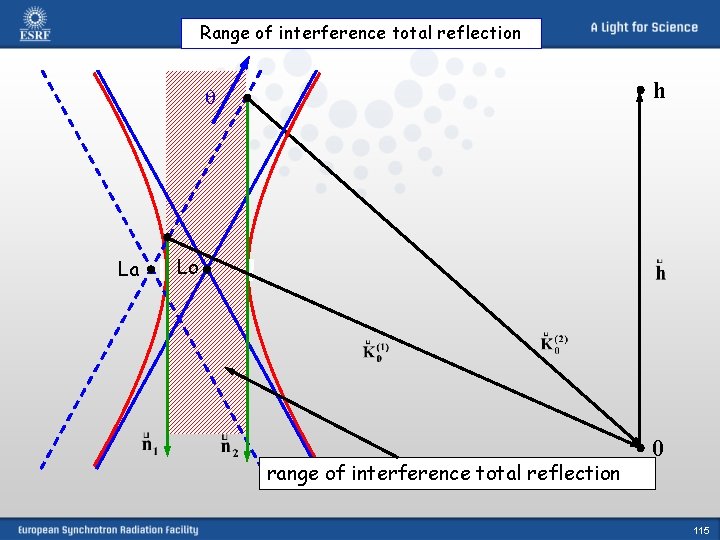
Dispersion surfaces in the two “beam” case – physically most important part h La Lo Reciprocal space 0 114

Range of interference total reflection h La Lo range of interference total reflection 0 115

Mathematics very simple to calculate a reflectivity curve for a semi-infinite crystal (Darwin solution) Normalised angular coordinate or deviation parameter: Full width at half maximum of the reflection curve: Refraction correction (middle of the reflection domain): 116

To be complete – Pendellösung length (general form): – other expression for the full width at half maximum of the reflection curve: 117

Integrated reflectivity No absorption, thick crystal (dynamical theory): Laue case: Bragg case: asymmetry factor: No absorption, thin crystal (kinematical limit): Both cases: 118

Integrated reflectivity Ri 1 2 3 t / 0 119

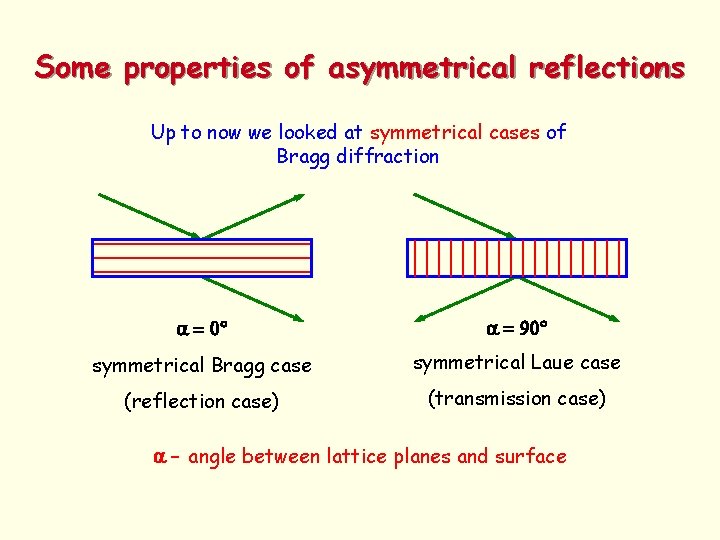
Some properties of asymmetrical reflections Up to now we looked at symmetrical cases of Bragg diffraction a = 0 a = 90 symmetrical Bragg case symmetrical Laue case (reflection case) (transmission case) a – angle between lattice planes and surface

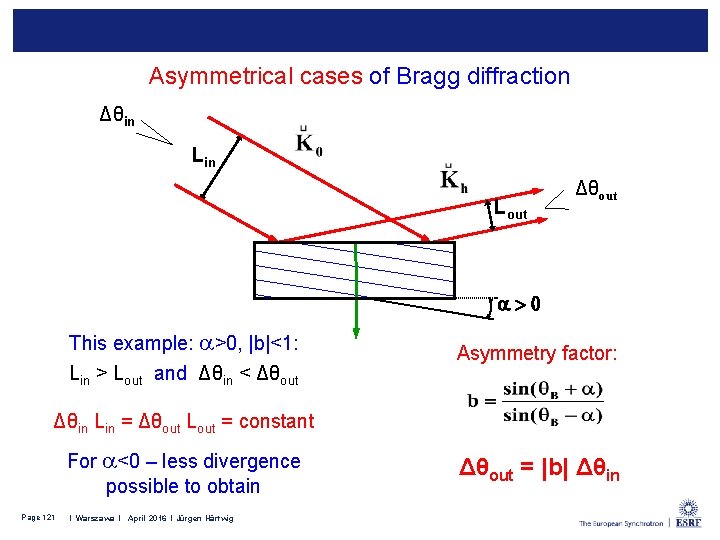
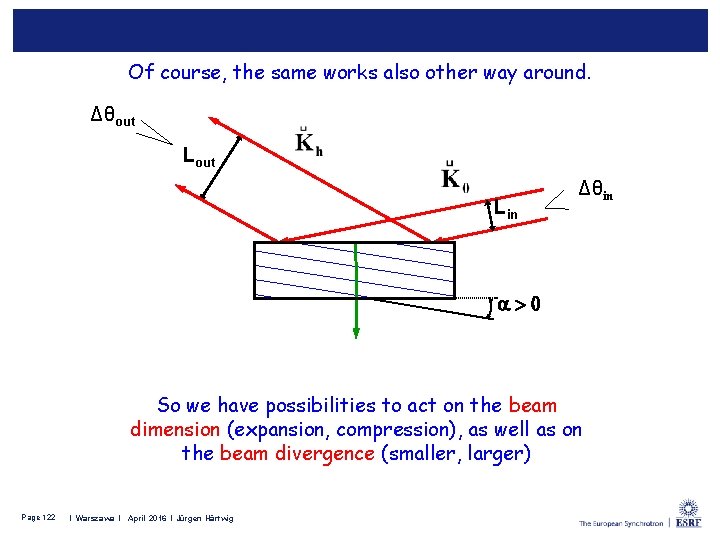
Asymmetrical cases of Bragg diffraction Δθin Lout Δθout a > 0 This example: a>0, |b|<1: Lin > Lout and Δθin < Δθout Asymmetry factor: Δθin Lin = Δθout Lout = constant For a<0 – less divergence possible to obtain Page 121 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig Δθout = |b| Δθin

Of course, the same works also other way around. Δθout Lin Δθin a > 0 So we have possibilities to act on the beam dimension (expansion, compression), as well as on the beam divergence (smaller, larger) Page 122 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig

But all is related and things have their price whin Lout whout Asymmetry factor: a > 0 This example: a>0, |b|<1: Lin > Lout and whin < whout = |b| whin Lin = whout Lout = constant Relation to symmetrical reflections right asymmetry (a<0) – less divergence possible to obtain whin = |b|-1/2 whsym whout = |b|1/2 whsym I Warszawa l April 2016 l Jürgen Härtwig

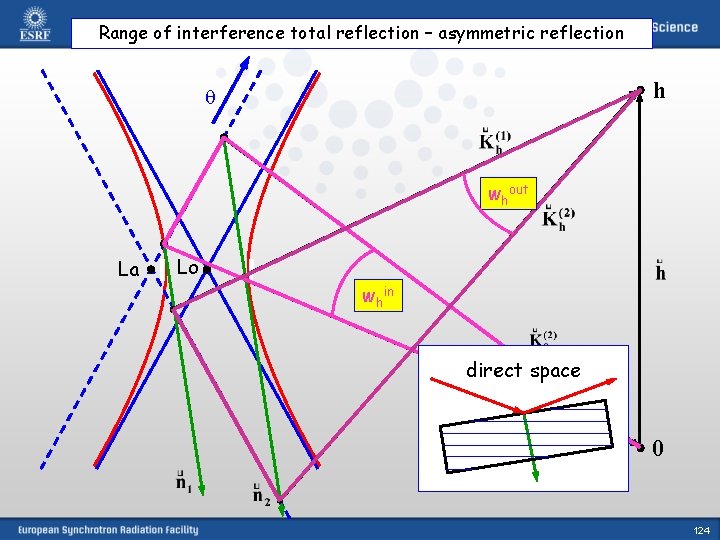
Range of interference total reflection – asymmetric reflection h whout La Lo whin direct space 0 124

EXAMPLE – ASYMMETRIC BRAGG DIFFRACTIONS BUT … Δθin Lin = Δθout Lout = constant This is too simple, hand-waving “derivation”. We need an additional dimension for the phase space. Besides sizes (widths Lx) and angles (Δθx) also wavelength, or energy, or wave number (ΔK) is needed Page 125 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig

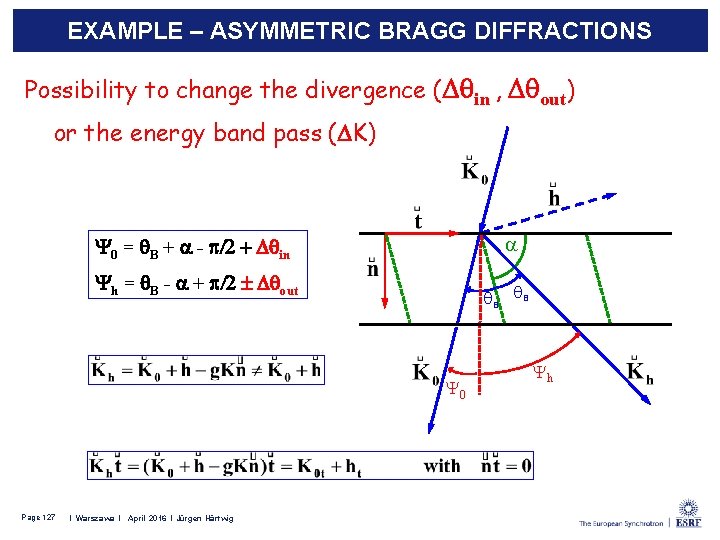
EXAMPLE – ASYMMETRIC BRAGG DIFFRACTIONS From electrodynamics (and dynamical diffraction theory) we know that: For the wave vectors outside the crystal: But for the tangential components - continuity: And remember, wave vectors depend on wavelength: Page 126 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig

EXAMPLE – ASYMMETRIC BRAGG DIFFRACTIONS Possibility to change the divergence ( in , out) or the energy band pass ( K) a 0 = B + a - p/2 + in h = B - a + p/2 out B B 0 Page 127 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig h

EXAMPLE – ASYMMETRIC BRAGG DIFFRACTIONS For small in, out and K we obtain (for Bragg and Laue case!): The divergence in and polychromaticity K/K of the incoming beam contribute to the divergence out of the outgoing beam An increased divergence out of the outgoing beam (with respect to that if the incoming beam) means: the source is virtually closer, or the source size is virtually larger, or the angular source size (see later) is virtually larger. Special case 1 Monochromatic, divergent incoming radiation K = 0, in 0 Page 128 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig out = |b| in

EXAMPLE – ASYMMETRIC BRAGG DIFFRACTIONS Special case 2 Polychromatic, “parallel” (plane wave) incoming radiation K 0, in = 0 We show later: “our (SR)” beams often are rather close to plane waves, but rather polychromatic 2. 1. out = 0 if cos( B - a) = cos( B + a) if a 0 (sym. Bragg case!) Only in the symmetric Bragg case the beam divergence is conserved for a polychromatic beam!!! Only in that case coherence is conserved!!! Only in that case focussing is not perturbed! Only in that case highest geometrical resolution possible! 2. 2 out 0 for all other cases A divergent, polychromatic beam is transformed in a even more divergent, polychromatic beam! Page 129 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig

Source size and angular source size are crucial parameters with respect to the character of the wave “seen” by the sample. angular source size d (d = s/p) not source divergence!! s p δ The angular source size is important for further physical properties: the geometrical resolution for imaging, the transversal coherence length, the demagnification limit of a “lens”. I Warszawa l April 2016 l Jürgen Härtwig

Image blurring due to non-zero source size angular source size: δ = s/p s δ p q geometrical resolution: ρ = q s/p = q δ s δ p q Spatial coherence Transversal coherence length: l. T = ½ λ p/s = ½ λ/δ I Warszawa l April 2016 l Jürgen Härtwig

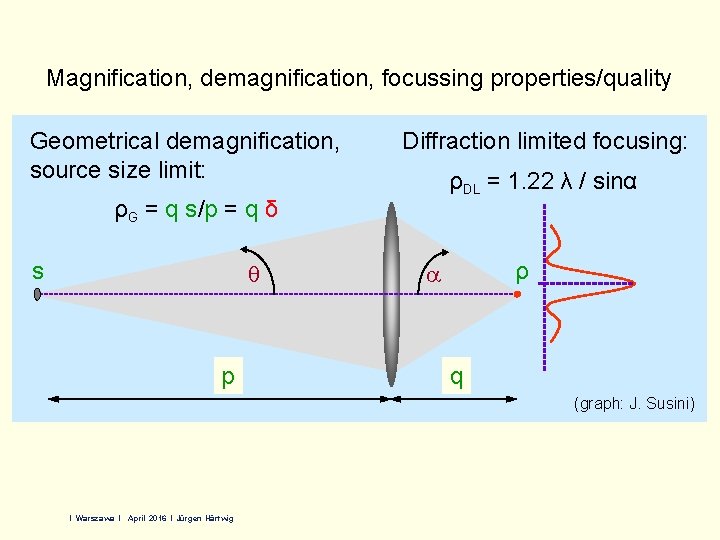
Magnification, demagnification, focussing properties/quality Geometrical demagnification, source size limit: Diffraction limited focusing: ρDL = 1. 22 λ / sinα ρG = q s/p = q δ s p ρ a q (graph: J. Susini) I Warszawa l April 2016 l Jürgen Härtwig

AT THE END – TWO BASIC QUESTIONS Two basic questions: What are “plane” or “divergent” waves? What are “monochromatic”, “polychromatic”, “white” beams/waves? For our monochromator and/or single crystalline sample! Reminder of basic physics Plane wave – infinite extend, wave front is plane, one wave vector perpendicular to it, delta-function in k-space. Monochromatic wave – wave train of infinite length, infinitely sharp spectral line, delta-function in ω-space. They do not exist in nature!!! Page 133 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig

AT THE END – TWO BASIC QUESTIONS The full width at half maximum of the reflectivity curve, is a good reference for our sample to define the character of a wave FWHM in angular space: R( ) wh FWHM in wavelength space: R( ) wh Page 134 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig

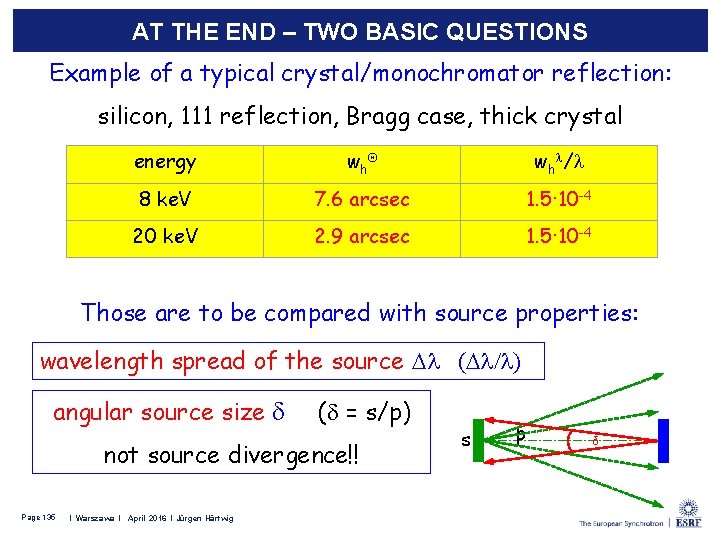
AT THE END – TWO BASIC QUESTIONS Example of a typical crystal/monochromator reflection: silicon, 111 reflection, Bragg case, thick crystal energy wh / 8 ke. V 7. 6 arcsec 1. 5· 10 -4 20 ke. V 2. 9 arcsec 1. 5· 10 -4 Those are to be compared with source properties: wavelength spread of the source ( / ) angular source size d (d = s/p) not source divergence!! Page 135 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig s p δ

AT THE END – TWO BASIC QUESTIONS relative wave length spread of the source / ( E/E) << FWHM in wavelength space “monochromatic” wave angular source size d = s/p << FWHM in angular space “plane” wave Page 136 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig

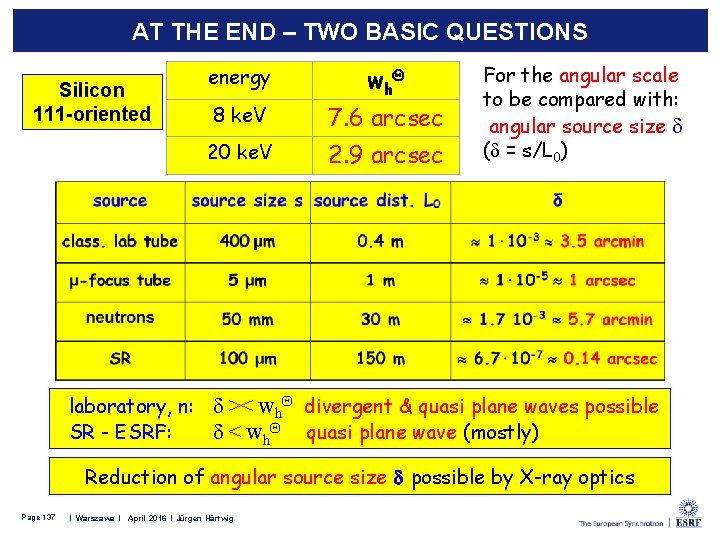
AT THE END – TWO BASIC QUESTIONS Silicon 111 -oriented energy wh 8 ke. V 7. 6 arcsec 20 ke. V 2. 9 arcsec For the angular scale to be compared with: angular source size d (d = s/L 0) laboratory, n: d >< wh divergent & quasi plane waves possible SR - ESRF: d < wh quasi plane wave (mostly) Reduction of angular source size d possible by X-ray optics Page 137 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig

AT THE END – TWO BASIC QUESTIONS relative wavelength or energy spread of the source / energy wh / 8 ke. V 1. 5· 10 -4 20 ke. V 1. 5· 10 -4 SR–white beams: / >>> wh really polychromatic ”monochromatic” beam (SR or laboratory): / <? > wh often not monochromatic (for all reflections narrower than the 1. 5· 10 -4 for silicon 111) special effort is necessary to approximate “monochromaticity” Page 138 I Leiden l February 2015 l Jürgen Härtwig I Warszawa l April 2016 l Jürgen Härtwig

LITERATURE Literature books W. H. Zachariasen, Theory of X-ray diffraction in crystals New York: John Wiley 1945 Dover Publications, Inc. , New York 1994 (unchanged edition 1945) M. Fatemi, NRL Report 7556 (1973) Explanatory Notes on “W. H. Zachariasen’s “Theory of X-ray Diffraction in Ideal Crystals” M. von Laue, Röntgenstrahl-Interferenzen Frankfurt am Main: Akademische Verlagsgesellschaft 1960 L. V. Azaroff, X-ray Diffraction New York: Mc. Graw-Hill Book Company 1974 Z. G. Pinsker, Dynamical scattering of X-rays in crystals Berlin: Springer Verlag 1978 (earlier 2 editions in Russian) A. Authier, Dynamical theory of X-ray diffraction Oxford Univ. Press 2001, 2005 (2 nd ed. ) the most complete monograph U. Pietsch, V. Holy, T. Baumbach, High Resolution X-ray Scattering, Springer, Berlin 2004 (thin films, nanostructures) 139

LITERATURE classic works (first and most current dynamical theories – for perfect crystals!!!) C. G. Darwin, The theory of X-ray reflection, Phil. Mag. 27, 315, 675 (1914) P. P. Ewald, Zur Begründung der Kristalloptik Teil I Dispersionstheorie Teil II Theorie der Reflexion und Brechung Teil III Die Kristalloptik der Röntgenstrahlen Ann. Phys. (Leipzig) 49, 1, 117 (1916); 54, 519 (1917) (English translations exist!) M. von Laue, Die Theorie der Röntgenstrahlinterferenzen in neuer Form Ergebn. Exakt. Naturwiss. , 10, 133 (1931) review articles R. W. James, The Dynamical Theory of X-ray Diffraction Solid State Physics 15, 55 (1963) B. W. Batterman & H. Cole, Dynamical diffraction of X-rays by perfect crystals Rev. Mod. Phys. 36, 681 (1964) A. Authier, Ewald waves in theory and experiment Adv. Struct. Res. Diffr. Methods 3, 1 (1970) A. Authier, Dynamical Theory of X-ray Diffraction International Tables for Crystallography, Volume B, Part 5. 1, 464 (1993) A. M. Afanas'ev, R. M. Imamov & E. K. Mukhamedzanov, Asymmetric X-ray Diffraction Cryst. Rev. 3, 157 (1992) 140

LITERATURE schools International Summer School on X-ray Dynamical Theory and Topography August 18 -26, 1974, Limoges, France X-ray and Neutron Dynamical Diffraction - Theory and Applications April 9 -21, 1996, Erice, Italy ed. A. Authier, S. Lagomarsino, B. K. Tanner, Plenum Press, New York 1996 further classic works (deformed crystals, QFT) P. Penning, D. Polder, Anomalous Transmission of X-rays in Elastically Deformed Crystals Philips Res. Reports 16, 419 (1961) P. Penning, Theory of X-ray Diffraction in Unstrained and Lightly Strained Perfect Crystals Thesis, Univ. Delft 1966, in Philips Res. Repts Suppl. 5, 1 -109 (1967) N. Kato, Pendellösung Fringes in Distorted Crystals I. Fermats Principle for Bloch Waves II. Application to the Two-Beam Case III. Application to Homogeneously Bent Crystals J. Phys. Soc. Japan 18, 1785 (1963), 19, 67, 971 (1964) S. Takagi, Dynamical Theory of Diffraction Applicable to Crystals with any Kind of Small Distortion Acta Cryst. 15, 1311 (1962) S. Takagi, A Dynamical Theory of Diffraction for a Distorted Crystal J. Phys. Soc. Japan 26, 1239 (1969) D. Taupin, Théorie dynamique de la diffraction des rayons X par les cristaux déformés Bull. Soc. Franc. Miner. Crist. 87, 469 (1964), Thesis: Paris 1964 M. Kuriyama, Theory of X-ray Diffraction by a Distorted Crystal J. Phys. Soc. Japan 23, 1369 (1967) 141

Thank you for your attention! HERCULES Grenoble, March 2009 142
 Motor learning theories
Motor learning theories Dynamical mean-field theory
Dynamical mean-field theory Dynamical systems neuroscience
Dynamical systems neuroscience Barycentric dynamical time
Barycentric dynamical time Discrete dynamical systems examples
Discrete dynamical systems examples Dynamical
Dynamical Automata
Automata Siam conference on applications of dynamical systems
Siam conference on applications of dynamical systems Kinematical theory of diffraction
Kinematical theory of diffraction Xray mastoid townes view
Xray mastoid townes view The purpose of a lead foil sheet in the film packet is
The purpose of a lead foil sheet in the film packet is Plain film kub
Plain film kub Xray xml editor
Xray xml editor Sza xray
Sza xray Jfk xray
Jfk xray Tetralogy of fallot xray
Tetralogy of fallot xray Osteoid definition
Osteoid definition Pulmonary embolism x ray
Pulmonary embolism x ray Rhese method positioning
Rhese method positioning Smv sinuses
Smv sinuses Xray technique chart
Xray technique chart Double exposure xray
Double exposure xray Falling load generators
Falling load generators Lara xray
Lara xray Artifact
Artifact Spectrum xray
Spectrum xray Asd vs pulmonary stenosis murmur
Asd vs pulmonary stenosis murmur Signo rigler
Signo rigler Noi toi poi doi
Noi toi poi doi Unilaterallt
Unilaterallt Xray file cabinet
Xray file cabinet Gimp xray
Gimp xray Darkroom entrance
Darkroom entrance Hampton hump sign คือ
Hampton hump sign คือ First xray ever taken
First xray ever taken Pterigoid plate
Pterigoid plate Xray laser
Xray laser Xray laser
Xray laser Triboluminescence scotch tape
Triboluminescence scotch tape Xray laser
Xray laser Xray spectrometer
Xray spectrometer Xray laser
Xray laser Xray laser
Xray laser Haustra xray
Haustra xray Xray laser
Xray laser Xray laser
Xray laser Xray laser
Xray laser Bga xray
Bga xray Acanthioparietal
Acanthioparietal Peter mueller mit
Peter mueller mit 68 xray
68 xray Double bubble sign
Double bubble sign Vena cava syndrome
Vena cava syndrome Facial bones positioning
Facial bones positioning Picker xray
Picker xray Difosfonate
Difosfonate Atom xray
Atom xray Silicon valley xray
Silicon valley xray Xps instrument
Xps instrument Who discovered x rays
Who discovered x rays Properties of xray
Properties of xray Pnuemothorax xray
Pnuemothorax xray Xray van
Xray van Xray uranus
Xray uranus Michigan xray
Michigan xray Mmc xray
Mmc xray Aryepiglotic
Aryepiglotic Gladstone park xray
Gladstone park xray Properties of xray
Properties of xray Steeple sign
Steeple sign Talipes calcaneovarus
Talipes calcaneovarus Bravais lattices
Bravais lattices Unipolar generator
Unipolar generator Xray searches
Xray searches Xray training
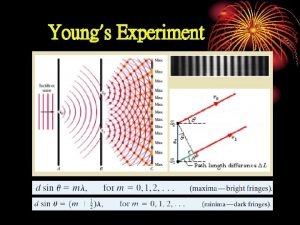
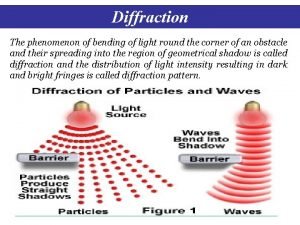
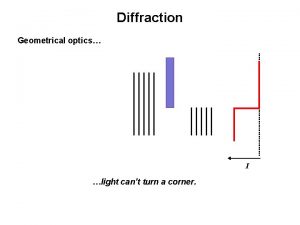
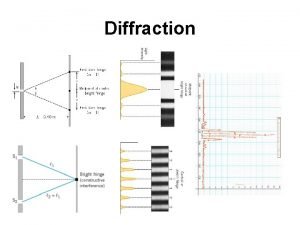
Xray training Diffraction
Diffraction Xray telescope
Xray telescope Xray gladstone
Xray gladstone Xray lithography
Xray lithography Inertia xray
Inertia xray Zenker's diverticulum xray
Zenker's diverticulum xray Thin film formula
Thin film formula Reflection refraction diffraction interference
Reflection refraction diffraction interference Cmedium
Cmedium Multiple slits diffraction
Multiple slits diffraction Magnets for neutron diffraction
Magnets for neutron diffraction Absent spectra in diffraction grating
Absent spectra in diffraction grating Dispersive power of a grating is
Dispersive power of a grating is Principal maxima and secondary maxima
Principal maxima and secondary maxima Sound diffraction
Sound diffraction Fraunhofer and fresnel diffraction
Fraunhofer and fresnel diffraction Diffraction
Diffraction Fresnel diffraction
Fresnel diffraction Missing order in diffraction
Missing order in diffraction Diffraction grating
Diffraction grating Diffraction in a sentence
Diffraction in a sentence Hkl
Hkl Diffraction pattern
Diffraction pattern Slit diffraction
Slit diffraction Bragg's diffraction condition in reciprocal lattice
Bragg's diffraction condition in reciprocal lattice Diffraction examples
Diffraction examples How are refraction and diffraction similar behaviors
How are refraction and diffraction similar behaviors Powder diffraction database
Powder diffraction database Diffraction through single slits derivation
Diffraction through single slits derivation Laser diffraction spectroscopy
Laser diffraction spectroscopy Huygens principle
Huygens principle Diffraction
Diffraction The phenomenon of diffraction can be understood using *
The phenomenon of diffraction can be understood using * Diffraction is the tendency of light to:
Diffraction is the tendency of light to: Calculation of critical angle
Calculation of critical angle Fraunhofer diffraction pattern circular aperture
Fraunhofer diffraction pattern circular aperture Diffraction
Diffraction Electron diffraction experiment results
Electron diffraction experiment results Diffraction and scattering
Diffraction and scattering Double slit diffraction
Double slit diffraction Slit diffraction
Slit diffraction Diffraction
Diffraction Diffraction peak
Diffraction peak Fig
Fig Slit diffraction
Slit diffraction Slit diffraction
Slit diffraction Dispersive power of grating
Dispersive power of grating Spatial outline
Spatial outline Diffraction of light
Diffraction of light Electron diffraction
Electron diffraction Diffraction grating
Diffraction grating Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Tư thế worm breton là gì
Tư thế worm breton là gì Chúa yêu trần thế
Chúa yêu trần thế Các môn thể thao bắt đầu bằng tiếng đua
Các môn thể thao bắt đầu bằng tiếng đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính thế năng
Công thức tính thế năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Cách giải mật thư tọa độ
Cách giải mật thư tọa độ 101012 bằng
101012 bằng Phản ứng thế ankan
Phản ứng thế ankan Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống