Homework 3 Xray diffraction Homework for chapter 6

Homework 3, X-ray diffraction Homework for chapter 6 (due Monday, Feb. 21). If not stated otherwise, assume l = 0. 154 nm (Cu. Ka-radiation) 1. van Holde 6. 1 2. van Holde 6. 2 a 3. van Holde 6. 5 4. van Holde 6. 6 5. van Holde 6. 10 6. You are working with a linear crystal of atoms, each spaced 6. 28 nm apart. You adjust your x-ray emitter so that it emits 0. 628 nm x-rays along the axis of the array. Below, S’ = 2 p. S, where S is the scattering vector we used in class. a. Using the Von Laue condition and the sphere of reflection, draw the allowed S’ vectors (S’ = k - k 0). Denote the direction of propagation of the x-rays as the positive z-axis. (k 0 is direction of incoming X-rays, S’ is scattering vector). b. You place a 1 cm 2 spherical detector 1 cm from the sample, centered on the z-axis, on the opposite side of the emitter. Draw the pattern you expect to detect. Clearly mark the expected distances. c. If you performed the experiment on a linear crystal with atoms spaced 0. 1 nm apart, what pattern would you detect? Would you have the same pattern if your detector were 1 m 2? What does this say about the resolution of your experiment?

Announcements • HW 3 (Chapter 6) due Fr. , Feb. 18 (not Feb. 11) • Midterm 1 is on Mo. , Feb. 28. Time: 5: 00 pm – Material: what we covered in class, HW – Ch. 1 -3, Ch. 6 • No class on Mo. , Feb. 14 & We. , Feb. 16 • Reading: Chapter 6 and the two Watson & Crick papers. • Movie and pizza this Wednesday at 6: 00 pm.

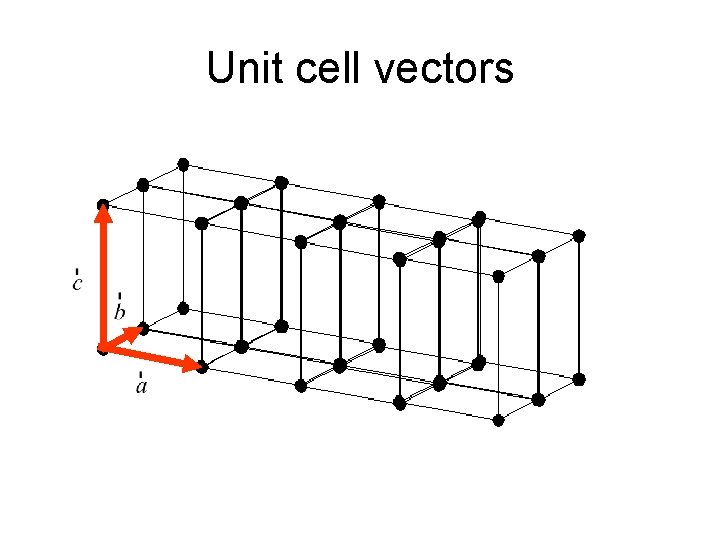
X-Ray diffraction What is a crystal? • Solids that are exact repeats of a symmetric motif (crystalline glass amorphous glass) • In a crystal, the level at which there is no symmetry asymmetric unit. • Apply rotational or screw operators to construct lattice motif. • Lattice motif is translated in three dimensions to form crystal lattice. • The lattice points are connected to form the boxes unit cell. • The edges define a set of unit vector axes • Angles between axes: unit cell dimensions a, b, c.

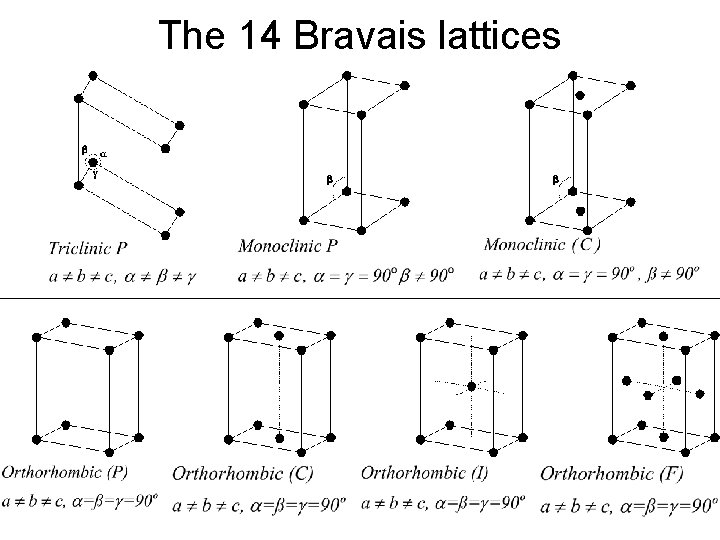
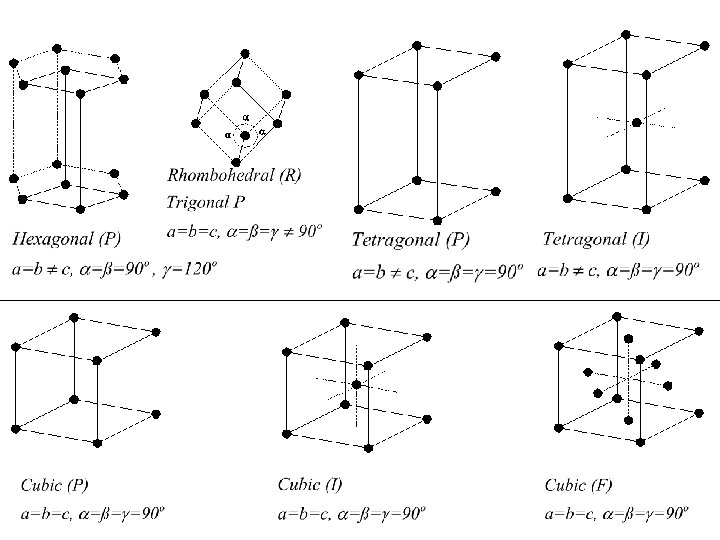
X-Ray diffraction What is a crystal? • Cystal stack unit cells repeatedly without any spaces between cells • Unit cell has to be a parallelepipid with four edges to a face, six faces to a unit cell. • All unit cells within a crystal are identical morphology of crystal is defined by unit cell • There are only seven crystal systems (describing whole crystal morphology): Triclinic, Monoclinic, Orthorhombic, Tetragonal, Trigonal, Hexagonal, Cubic. • There are only fourteen unique crystal lattices fourteen Bravais lattices. • P = primitive lattice point at corners of unit cell, F= face centered lattice point at all six faces, I = lattice point in center of unit cell, C = centered, lattice point on two opposing faces.

Unit cell vectors

The 14 Bravais lattices

Space groups • What symmetry operations (e. g. rotation axes, (2 -, 3 -, 4 -, 6 - fold axis, mirrors, inversion axes …, at corner, at face, …) can be applied to the unit cell (inside crystal)? This defines the 32 point groups of the unit cell (see Table 1. 4). • The combination of the 32 symmetry types (point groups) with the 14 Bravais lattice, yields 230 distinct space groups. • In biological molecules, there are really only 65 relevant space groups (no inversion axes or mirrors allowed, because they turn Lamino acids into D-amino acids. • The space group specifies the lattice type (outside crystal morphology) and the symmetry of the unit cell (inside). • Different crystals that have identical unit cell lengths and angles and are in the same space group are isomorphous.

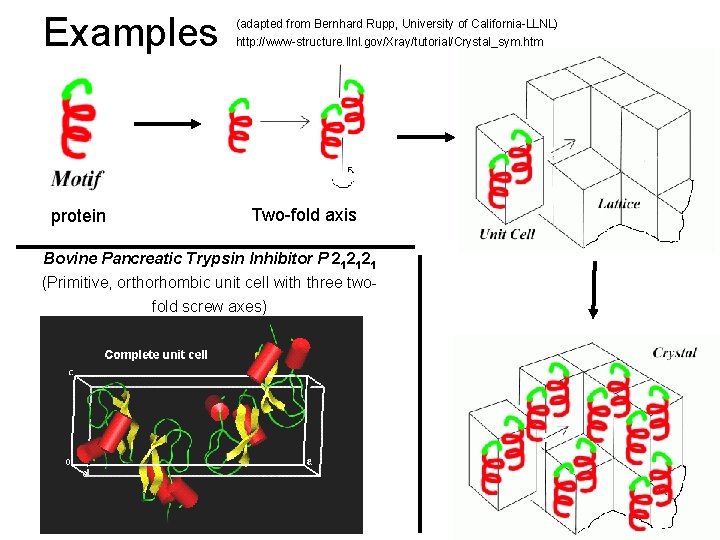
Examples protein (adapted from Bernhard Rupp, University of California-LLNL) http: //www-structure. llnl. gov/Xray/tutorial/Crystal_sym. htm Two-fold axis Bovine Pancreatic Trypsin Inhibitor P 212121 (Primitive, orthorhombic unit cell with three twofold screw axes)

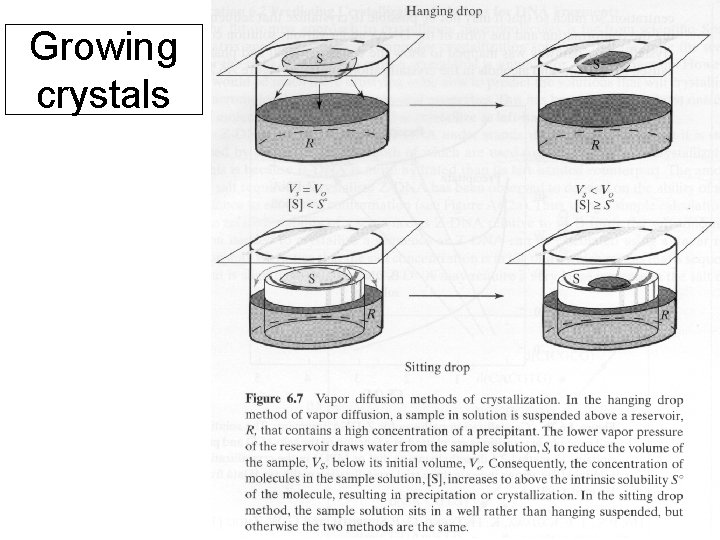
Growing crystals

Theory of X-ray diffraction • Treat X-Rays as waves (Cu. Ka l ~ 0. 154 nm). • Scattering: ability of an object to change the direction of a wave. • If two objects (A and B) are hit by a wave they act as a point source of a new wave with same wavelength and velocity (Huygens’ principle) • Diffraction: those two waves interfere with each other destructive and constructive interference. observe where maxima and minima are on screen get position of A and B

Bragg’s law (simple model of crystal, but it works!) Crystal is made up of crystal planes. • Assume a one-dimensional crystal. d Fig. 6. 10 Reciprocal relationship between the Bragg angle q and the spacing, d, between the lattice planes. We can use Bragg’s law to determine dimension of unit cell!

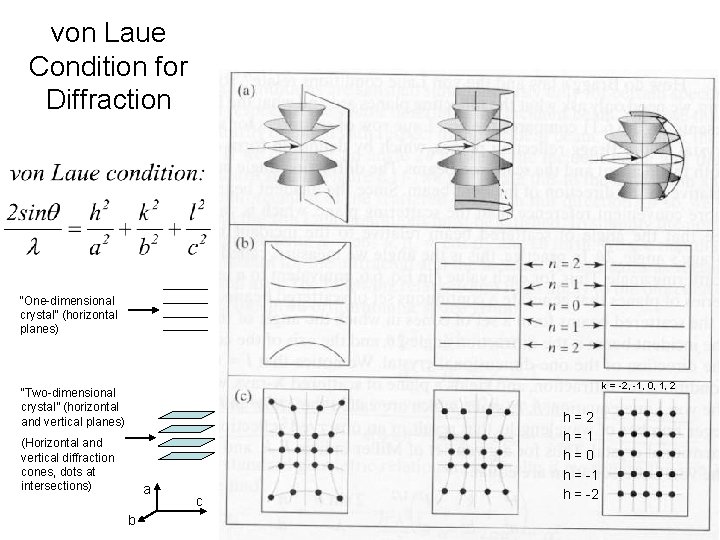
von Laue condition for diffraction Now we’ll move on to a three-dimensional crystal. Lattice still consists of only planes, but now we have a three-dimensional grid (still just dots, no internal structure, yet) In three dimensions (pp 263 -265): h, k, l, are the Miller indices. Every discrete diffraction spot on a film has a particular Miller index. E. g. reflection (1, 0, 0) h=1, k=l=0 Each cone (h=1, -1, 2, -2 …) 2 q is the angle measured from the incoming X-ray beam

von Laue Condition for Diffraction “One-dimensional crystal” (horizontal planes) k = -2, -1, 0, 1, 2 “Two-dimensional crystal” (horizontal and vertical planes) (Horizontal and vertical diffraction cones, dots at intersections) a b c h=2 h=1 h=0 h = -1 h = -2

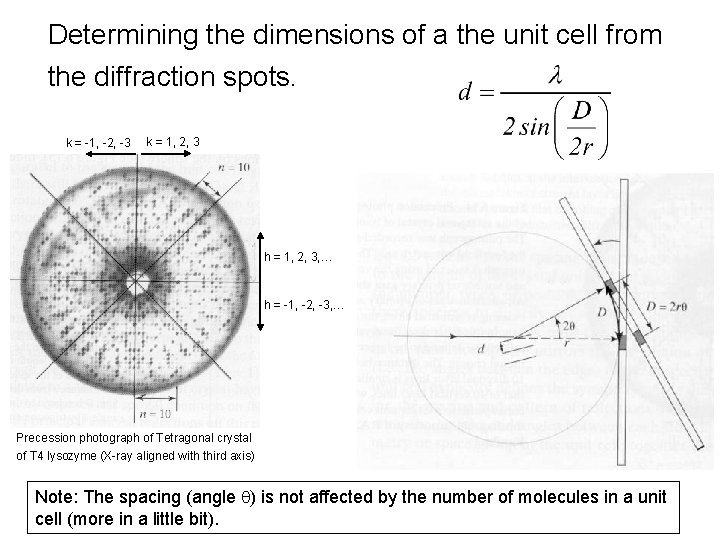
Determining the dimensions of a the unit cell from the diffraction spots. k = -1, -2, -3 k = 1, 2, 3 h = 1, 2, 3, … h = -1, -2, -3, … Precession photograph of Tetragonal crystal of T 4 lysozyme (X-ray aligned with third axis) Note: The spacing (angle q) is not affected by the number of molecules in a unit cell (more in a little bit).

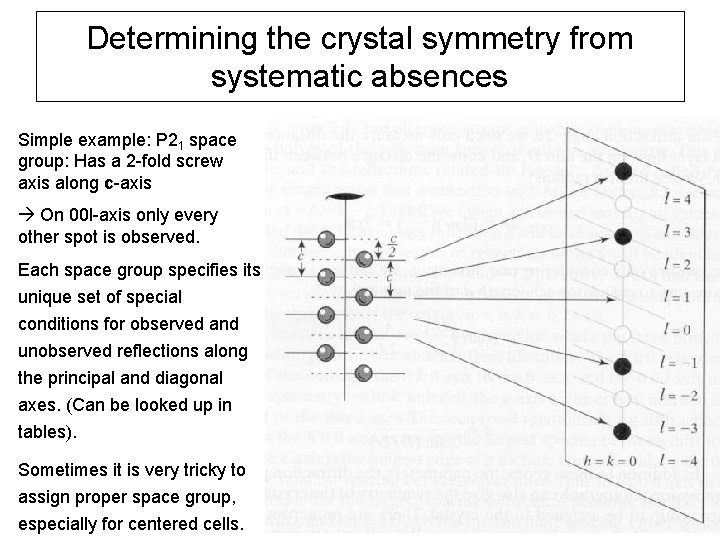
Determining the crystal symmetry from systematic absences Simple example: P 21 space group: Has a 2 -fold screw axis along c-axis On 00 l-axis only every other spot is observed. Each space group specifies its unique set of special conditions for observed and unobserved reflections along the principal and diagonal axes. (Can be looked up in tables). Sometimes it is very tricky to assign proper space group, especially for centered cells.

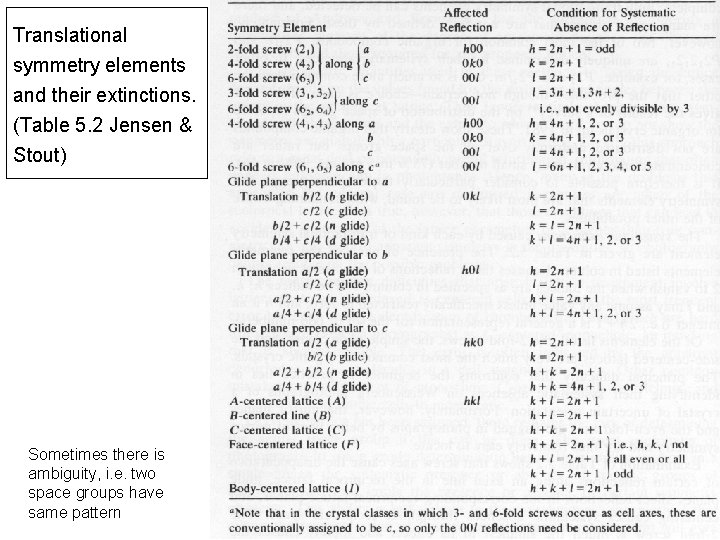
Translational symmetry elements and their extinctions. (Table 5. 2 Jensen & Stout) Sometimes there is ambiguity, i. e. two space groups have same pattern

Is Bragg’s law still valid for two or more atoms in a unit cell? Conceptually: Jensen and Stout Two atoms in a unit cell (reflect) waves from their respective planes. The waves combine and form a resultant wave, that looks like it has been reflected from the original unit cell lattice plane. Diffraction is spot is in the same place, but has different intensity (intensity of resultant wave). We assumed the electron density is in planes. In reality it is spread throughout the unit cell. Nevertheless, the derivation is still valid, since it can be shown that waves scattered from electron density not lying in a plane P, can be added to give a resultant as if reflected from the plane.

Morphology of a crystal • By observing the spacing and pattern of reflections on the diffraction pattern, we can determine the lengths, and angles between each side of the unit cell, as well as the symmetry or space group in the unit cell. • Still, how do we find out what’s inside the unit cell? (i. e. the interesting stuff, like proteins).

Solving macromolecular structures by X-ray diffraction • Now assume that we have more than one atom in a unit cell the diffraction angle q will remain the same!! q is independent on how many atoms we have in the unit cell!! The diffraction angle is still related to the unit cell dimension by Bragg’s law. • However, with one atom, the phase and amplitude of the resultant wave from each plane (atom) was the same. With more than one atom, the phase and amplitude coming from each plane of different atoms may be different, resulting in different intensities of the reflections. • Deconvolute each reflection into the phase and amplitude contributions from each of the individual reflections from each atom in the molecule. # of atoms in unit cell does NOT affect reflection angle (Bragg’s law). # of atoms (electron density) in unit cell DOES affect intensity of reflection spots.

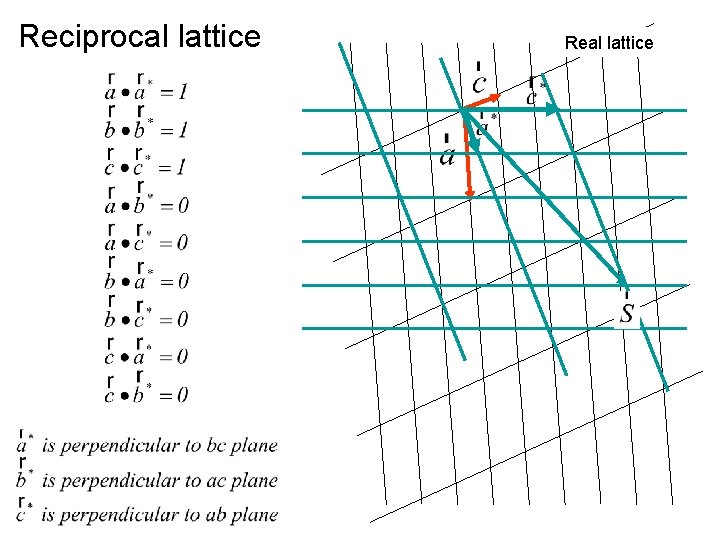
Reciprocal lattice Real lattice

Relationship between unit cell parameters in real space and in reciprocal space Stout & Jensen (1989) X-Structure Determination. A practical guide. 2 nd ed. John Wiley & Sons, New York

Relationship between unit cell parameters in real space and in reciprocal space Stout & Jensen (1989) X-Structure Determination. A practical guide. 2 nd ed. John Wiley & Sons, New York

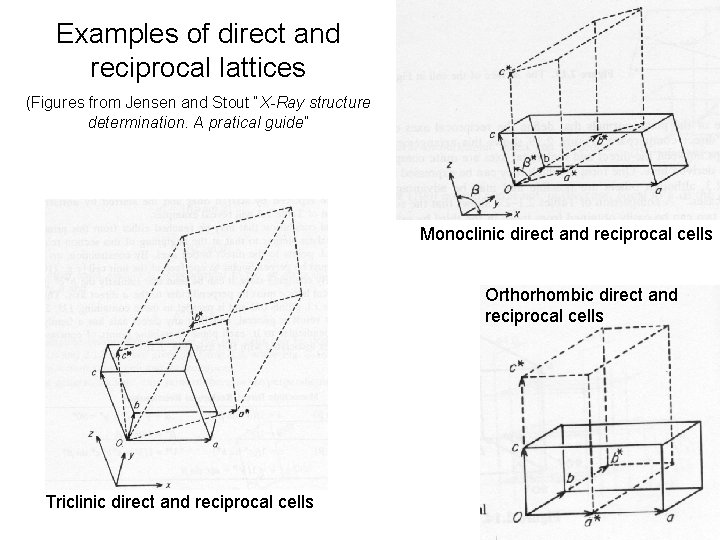
Examples of direct and reciprocal lattices (Figures from Jensen and Stout “X-Ray structure determination. A pratical guide” Monoclinic direct and reciprocal cells Orthorhombic direct and reciprocal cells Triclinic direct and reciprocal cells

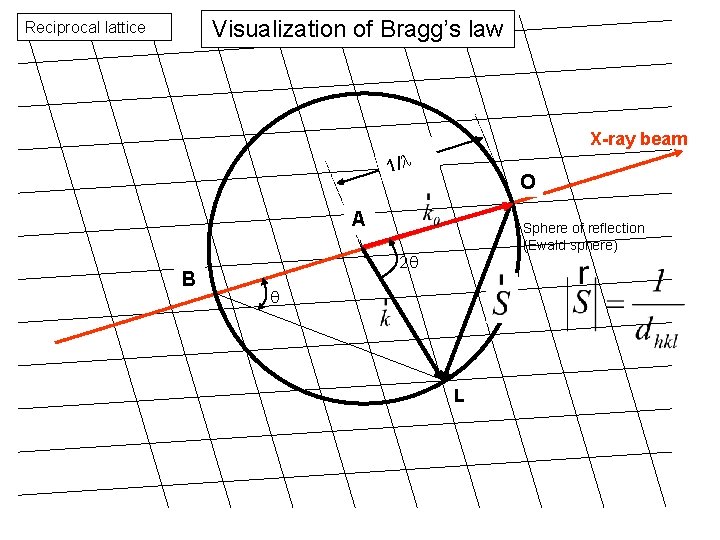
Visualization of Bragg’s law Reciprocal lattice X-ray beam 1/l O A B Sphere of reflection (Ewald sphere) 2 q q L

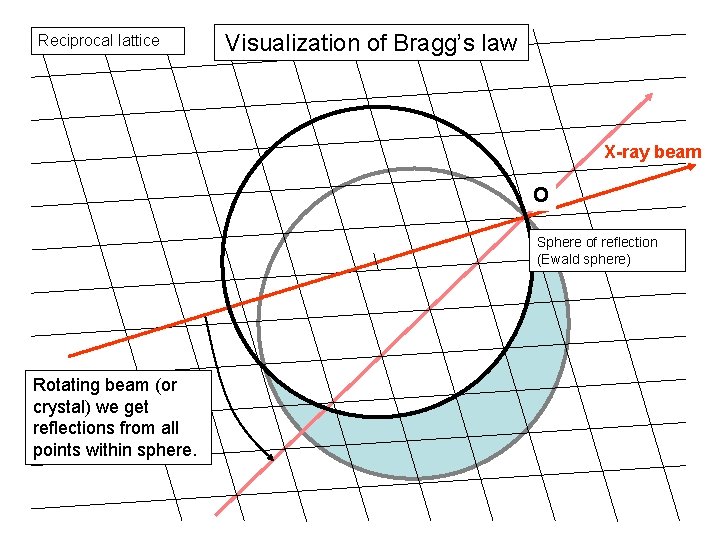
Reciprocal lattice Visualization of Bragg’s law X-ray beam O Sphere of reflection (Ewald sphere) Rotating beam (or crystal) we get reflections from all points within sphere.

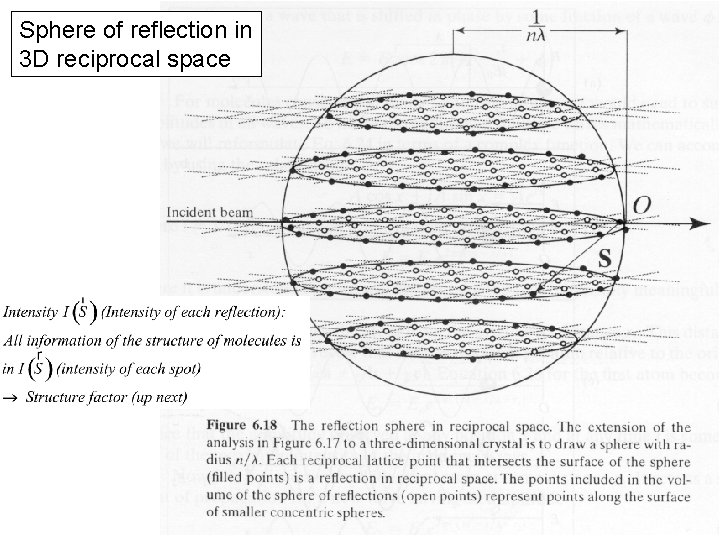
Sphere of reflection in 3 D reciprocal space

Definition of reciprocal lattice (hand out) Bragg’s law in reciprocal space

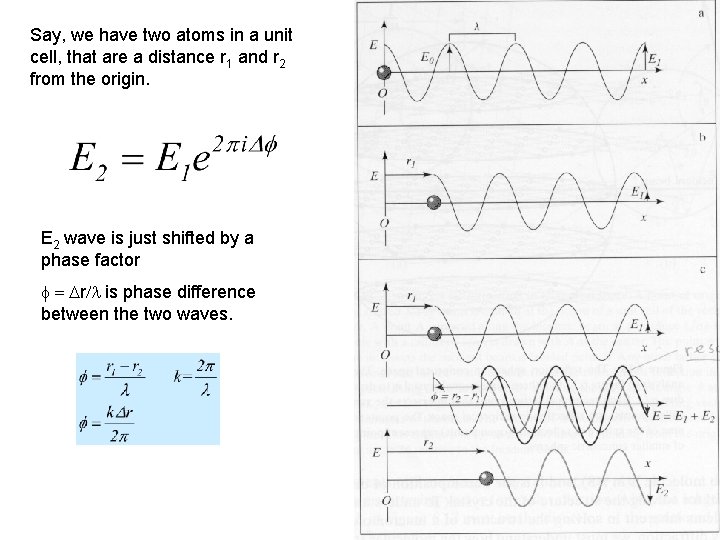
Say, we have two atoms in a unit cell, that are a distance r 1 and r 2 from the origin. E 2 wave is just shifted by a phase factor f = Dr/l is phase difference between the two waves.

Structure Factor for many atoms inside unit cell • F (hkl) is electric field amplitude for a certain scattering direction (reflection spot h, k, l on film) • x, y, z … fractional coordinates describing the position of each atom inside unit cell. • fj is the amplitude of the electric field coming from each atom j inside unit cell (amplitude is proportional to electron density). • The sum is over all N atoms inside a unit cell. • S = (ha*, kb* lc*) is the scattering vector for each diffraction spot

Moving from fixed points to electron density inside a cell • The sum is replaced by an integral over the volume of the unit cell, V. • the amplitude fi is replaced by the electron density r(r) (the more density the larger the amplitude). This is very nice now: If we know the electron density r(r) (i. e. positions of atoms) inside unit cell, we can predict the intensity, of each reflection spot (h, k, l) on the film Knowing the size of the unit cell, and knowing the electron density, we can calculate (predict) the location and intensity of each diffraction spot.

Starting with the equation for the structure factor F(hkl), show that the intensity of reflections along the (h 00) axis will be zero for all odd values of h, when a two-fold screw axis is aligned along the cystallographic a-axis.

Moving from the structure factor to the electron density (final goal). • We need to do the ‘Fourier transform’ of the structure factor to get the electron density out. Now, the diffraction pattern is actually made up of points, so the integral becomes a sum (Fourier series) over all diffraction spots: And that is what we want!!

… but wait, there is a problem …the phase problem • We cannot measure F(hkl), only |F(hkl)|. • We can measure the intensity I(hkl) of the spots We only know the magnitude but not the direction (phase a) of F(S). We have lost the phase. How bad is that? Pretty bad, because we can calculate the “magnitude” of the electron density, but we don’t know where it is in the unit cell. What can we do? ?

Electron density calculate from the two components of F(hkl). (a) Using only [F(hkl)]. The map does not fit the actual structure (Patterson map like). (b) Using only the phase information ([F(hkl)] was set to 1).

Phase problem solutions • Molecular replacement: – If we are lucky, you can get hold of the structure of a known, isomorphous crystal. – This is often used when one wants to know the effect of a mutation in a crystal, or when one wants to know where a substrate binds (soak substrate into crystal). – We use the structure (r (r)) of the known crystal as a starting point. – Iterative solution: Make small changes to known structure (r(r)), calculate new diffraction pattern (I(hkl), compare to data (diffraction pattern of new crystal), adjust known structure (r(r)), again, calculate new diffraction pattern (I(hkl)), compare with data, … etc.

Patterson map (Patterson, 1935) • We can get the relative (not absolute) positions of atoms with respect to each other from a Patterson map. • The Patterson function (autocorrelation of electron density with itself) • The Patterson function has peaks in a Patterson contour map that correspond to the vector differences between the atomic positions • If N atoms in unit cell, Patterson map has N 2 peaks (N at origin, and N(N-1) off-origin, some off-origin can still be on top of each other).

Patterson Map (a) Two atoms in a unit cell (b) Patterson map for those two atoms (b) (c) Two additional atoms (created by two-fold symmetry) (c) (d) Patterson map for structure in (c).

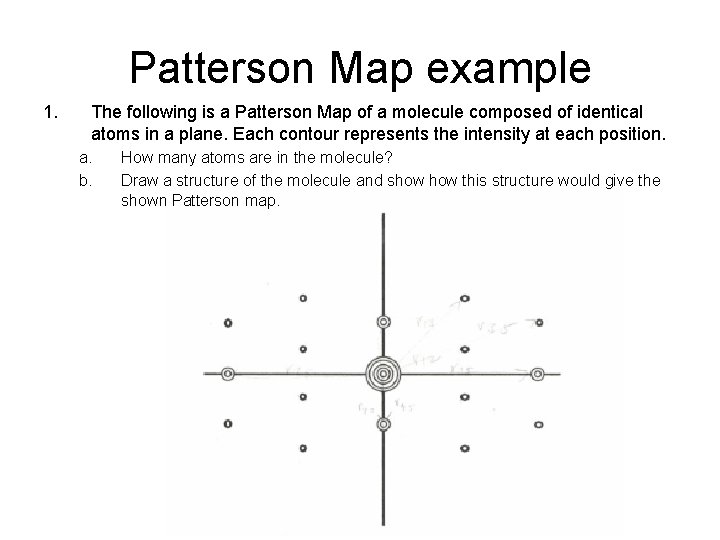
Patterson Map example 1. The following is a Patterson Map of a molecule composed of identical atoms in a plane. Each contour represents the intensity at each position. a. b. How many atoms are in the molecule? Draw a structure of the molecule and show this structure would give the shown Patterson map.

Multiple Isomorphous Replacement 1. 2. 3. 4. 5. 6. Collect the diffraction data from native crystal. Soak in a heavy atom and collect diffraction data. By comparing those two data sets, the position and the phase of the heavy metals can often be figured out (because they are very strong scatterers). Repeat with other heavy atom derivatives. These data sets can then be used to estimate the phases of the native data set. Do iterative improvements (estimate position and phases, calculate diffraction spots, compare with data, estimate improved positions and phases, calculate diffraction spots, etc…)

Structure refinement, the R-factor • The R-factor is defined as: • It’s the error between the real diffraction pattern and the calculated one. • A R-factor of ~0. 2 (20% error) is considered good enough to give a good model of the structure.

“Resolution in X-Ray Crystallography” There are several issues: 1. Smallest d in Bragg’s law, 2 sinq = l/d, d ~0. 094 nm for q = 110° Cu. Ka-radiation (l = 0. 154 nm) and largest practical angle 2 q = 110° 2. The “resolution” of X-ray diffraction is also limited by being able to separate spots on film. Reflection spots must be separated by at least 2° (because of their own size, ~ 1° at half-height). 2 sinq = l/dunit cell. For larger unit cells, need to use larger l (Cu. Ka over Mo. Ka). 3. How many data points (reflections) are required to obtain atomic resolution? We need (at least) 4 N equations to solve for 4 N parameters (x, y, z and temperature factor B for each of the N atoms within unit cell). Need at least 4 N good reflection spots on film. Need at least 4 N reciprocal # of points inside limiting sphere: lattice points inside sphere of reflection. Bragg’s law: d=2 lsinq Where d is resolution (smallest distance between planes) V is volume of real lattice.

# of unique reflections on film • If we get N* reflections on film, some of them are redundant because of symmetry. • Friedel’s law: I(hkl) = I(–h –k –l) • Each symmetry operator reduces # of unique reflections (For P 212121, only 1/8 the reflections are unique). • Good news: because of symmetry, not the whole unit cell needs to be solved.

Example The precession photograph in Fig. 6. 14 was recorded with a crystal to film distance of 7. 65 cm and the spacing between reflections was measured to be 0. 15 cm. The third dimension for this crystal is 3. 777 nm. 1. Calculate the unit cell dimensions of this crystal. 2. Propose one possible space group for this crystal. 3. If the third axis has 41 symmetry, what systematic absences would you expect to see? 4. Estimate the number of unique reflections one would expect for a data set at 0. 133 nm resolution.

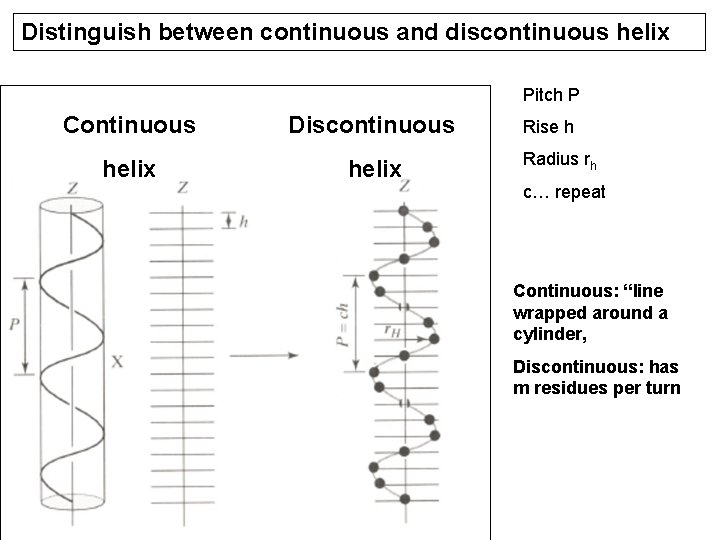
Fiber diffraction • If there is inherent symmetry in a molecule (i. e. long helical biopolymers) X-Ray diffraction patterns can be obtained from non-crystalline samples. • Like one-dimensional crystal along helix axis. • We can treat an exact repeat of helix (i. e. one residue) as a crystalline unit cell. • Can get information about helical symmetry, pitch and radius. • Meridianal reflections: information on pitch and symmetry • Equatorial reflections: radius of helix

Distinguish between continuous and discontinuous helix Pitch P Continuous Discontinuous helix Rise h Radius rh c… repeat Continuous: “line wrapped around a cylinder, Discontinuous: has m residues per turn

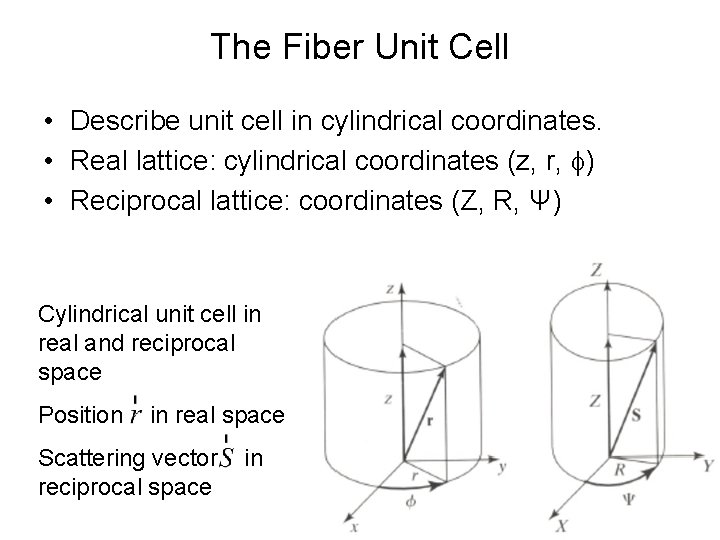
The Fiber Unit Cell • Describe unit cell in cylindrical coordinates. • Real lattice: cylindrical coordinates (z, r, f) • Reciprocal lattice: coordinates (Z, R, Ψ) Cylindrical unit cell in real and reciprocal space Position in real space Scattering vector reciprocal space in

The structure factor in cylindrical coordinates - Now, we’ll assume a continuous helix: - Helix is a line wrapped around a cylinder (r is zero if not on line) - Unit cell has a length equal to the pitch of helix.

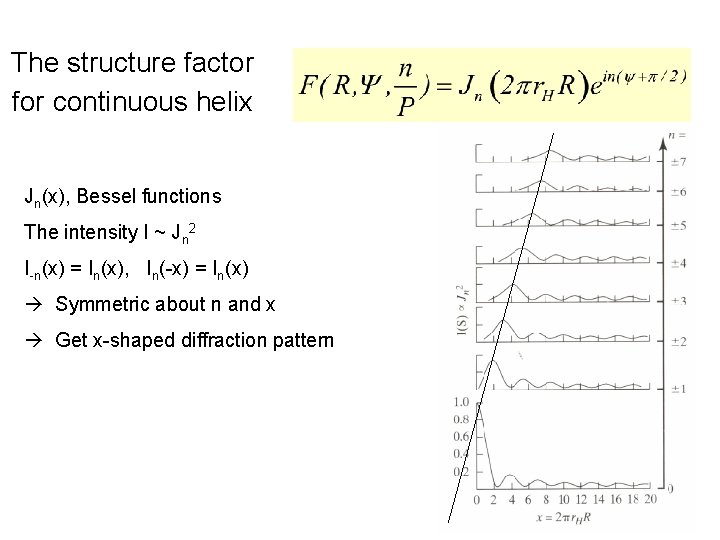
The structure factor for continuous helix Jn(x), Bessel functions The intensity I ~ Jn 2 I-n(x) = In(x), In(-x) = In(x) Symmetric about n and x Get x-shaped diffraction pattern

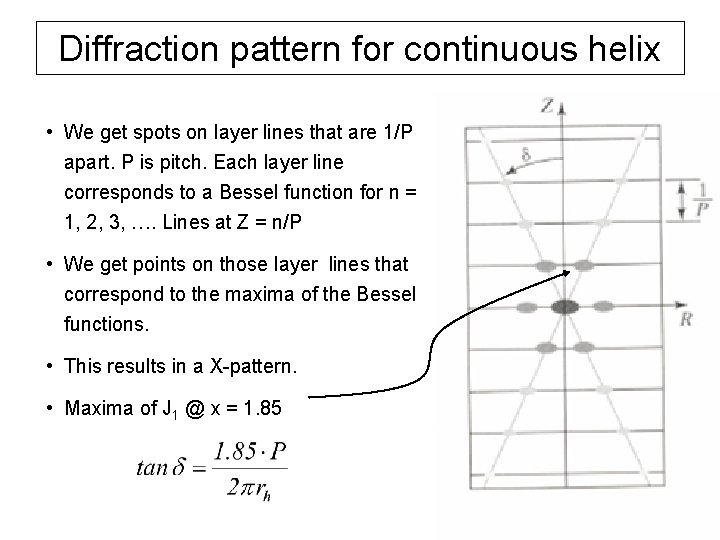
Diffraction pattern for continuous helix • We get spots on layer lines that are 1/P apart. P is pitch. Each layer line corresponds to a Bessel function for n = 1, 2, 3, …. Lines at Z = n/P • We get points on those layer lines that correspond to the maxima of the Bessel functions. • This results in a X-pattern. • Maxima of J 1 @ x = 1. 85

Diffraction pattern for discontinuous helix with integral number of m residues, per repeat c. • The X-pattern we got for the continuous helix will just repeat itself on the Z-axis with spacing Z=c/P • Examples: – B-DNA: c = 10 residues/turn – A-DNA: c = 11 residues/turn – 310 -helix: c = 3 residues/turn • Each layer line is still spaced at 1/P • The pattern is repeated at Z = c/P = 1/h

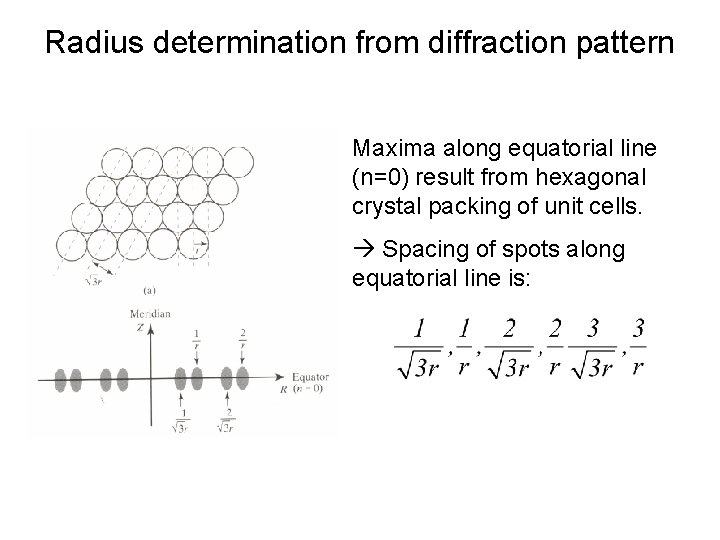
Radius determination from diffraction pattern Maxima along equatorial line (n=0) result from hexagonal crystal packing of unit cells. Spacing of spots along equatorial line is: