Kinematical diffraction theory Kinematical theory of diffraction choice

Kinematical diffraction theory

Kinematical theory of diffraction - choice of theory to descrie diffraction depends on - diffraction angle - intensity of the radiation - wavelength of the radiation - kinematic theory for large diffraction angles (2 q > 5 … 10°), low intenisty -> BORN approximation - assumptions: - single diffraction (photon interacts with EXACTLY one electron) -> i. e. the transmitted beam is not diffracted - large diffraction vector - weak scattering applicability of the Maxwell equations - index of refraction n = 1 - Gauss-distribution of the surface roughness of the sample (rms-roughness) - interaction cross section ds of the scattering: How much of the incident radiation is scattered in direction (d. W) of the detector. T = scattering potential of the atoms

Kinematical theory of diffraction Limits! - for high penetration depths, scattering increases: -> kinematic theory may loose ist applicability due to multiple scattering - for small diffraction vectors, absorption and dispersion cannot be treated independently from each other anymore -> not part of kinematical theory

Kinematical theory of diffraction - scattering - Thomson-scattering: free e- are excited by an incident photon and, due to their oscillations, emits photons themselves - no change in energy across the whole process - electrons scatter the incident wave - diffraction - combination of scattered waves - requires translational periodic lattice in order to create constructive interference along certain directions - intensity gains a well measurable magnitude

Kinematical theory of diffraction Laue - conditions - mathematical description of a 3 D lattice - R = ua+vb+wc (translation periodicity) r*=ha*+kb*lc* (reciprocal lattice) - electron density distribution in the crystal: - amplitude of the wave scattered by the whole crystal - amplitude ≠ 0, only when reciprocal position vector (for whom the amplitude is calculated) coincides with a reciprocal lattice point - with r*=(s-s 0)/l: - = Laue-conditions: change of wave vector during the diffraction process equals a reciprocal lattice vector (one condition for each direction in 3 D)

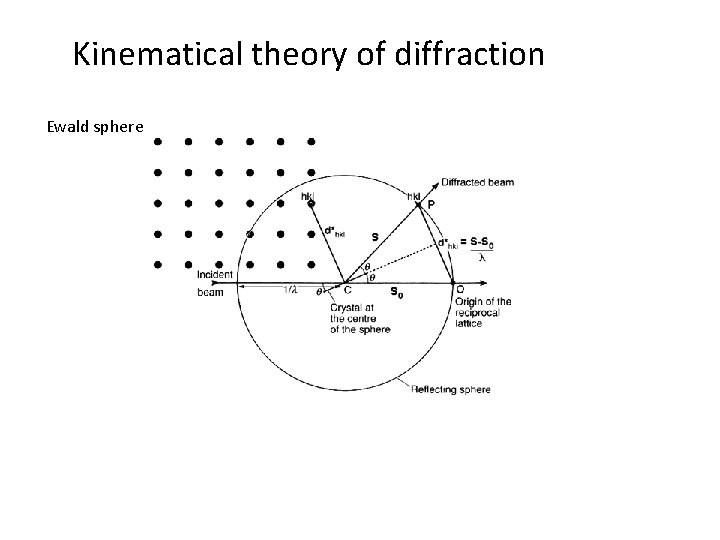
Kinematical theory of diffraction Ewald sphere

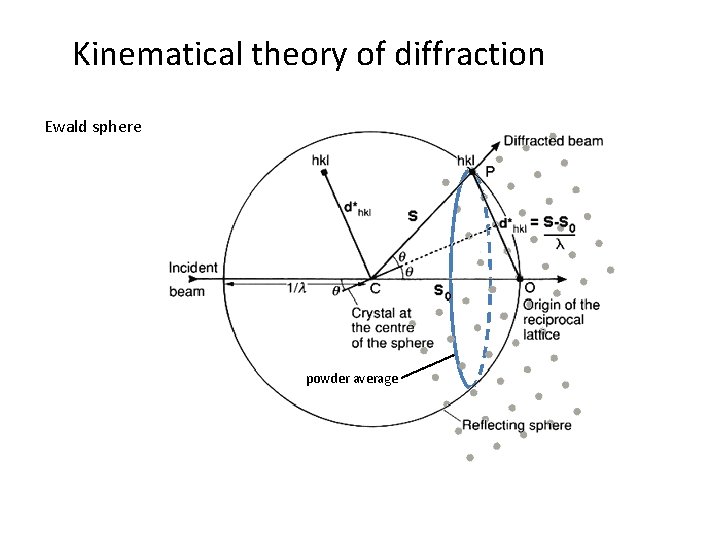
Kinematical theory of diffraction Ewald sphere powder average

Kinematical theory of diffraction Ewald sphere

Kinematical theory of diffraction Ewald sphere

Kinematical theory of diffraction limited range - only reciprocal lattice points whose distance is < 2 ks from the origin of the reciprocal space are able to get into reflection condition - the Ewald sphere is large enough to include reciprocal lattice points only for small wavelengths (Laue conditions) : no diffraction with visible light at crystal lattices

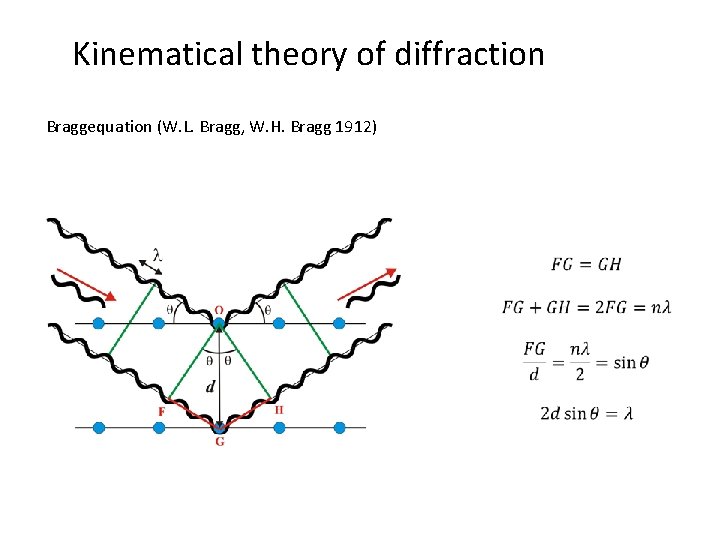
Kinematical theory of diffraction Bragg equation (W. L. Bragg, W. H. Bragg 1912) - interference of X-rays being scattered at atoms on lattice planes - path difference between waves diffracted at two neighbouring lattice planes: 2 d sin q - constructive interference if this path difference is kl describes the same phenomenon as the Laue conditions but with a different approach -> results in the same consequences

Kinematical theory of diffraction Braggequation (W. L. Bragg, W. H. Bragg 1912)

Kinematical theory of diffraction Bragg equation (W. L. Bragg, W. H. Bragg 1912) propagation of the diffracted wave 2 D-translation lattice of scatterers

Kinematical theory of diffraction Bragg equation (W. L. Bragg, W. H. Bragg 1912) 2 D-translation lattice of scatterers (lattice strain)

Kinematical theory of diffraction Bragg equation (W. L. Bragg, W. H. Bragg 1912) 3 D-translation lattice of scatterers

Kinematical theory of diffraction Bragg equation (W. L. Bragg, W. H. Bragg, 1912) 2 D-translation lattice of scatterers

Kinematical theory of diffraction Kinematically scattered intensity total scattered intensity by a powder sample consisting of i phases - S … scale factor m … multiplicity of lattice planes L … Lorentz factor P … polarisation factor A … absorption correction F … structure factor <u²> … atomic displacements

Kinematical theory of diffraction scale factor - contains contributions of Thomson scattering - depends on primary intensity and the instrumental setup - corresponds to the intensity scattered into a solid angle r … Abstand Probe-Detektor - integration across all solid angles: total scattered intensity - P/I 0 = 6. 7· 10 -25 cm 2: scattering cross section for Thomson scattering - i. e. 2 % of the incident intensity are diffracted (crystal < 1 mm, only free e -)

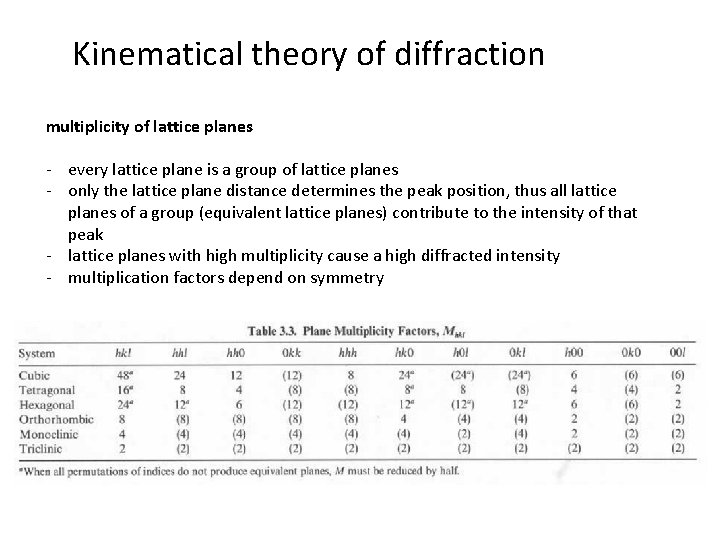
Kinematical theory of diffraction multiplicity of lattice planes - every lattice plane is a group of lattice planes - only the lattice plane distance determines the peak position, thus all lattice planes of a group (equivalent lattice planes) contribute to the intensity of that peak - lattice planes with high multiplicity cause a high diffracted intensity - multiplication factors depend on symmetry

Kinematical theory of diffraction Lorentz, polarisation and absorption correction - change of intensity due to partially polarised radiation with monochromator - duration of a reciprocal latttice point fulfilling the diffraction condition single crystal powder - correction of different path lengths in the sample at different angles 2 q for symmetrical geometry: A = (2µ)-1

Kinematical theory of diffraction structure factor - how is the intensity of the diffracted radiation affected by the atomic arrangement - contains amplitudes and phases is a complex quantity N … number of atoms in the unit cell - combines information from direct and reciprocal space - more explicit: - structure factor is the Fourier transform of the scattering power of a unit cell (distribution of electron density)

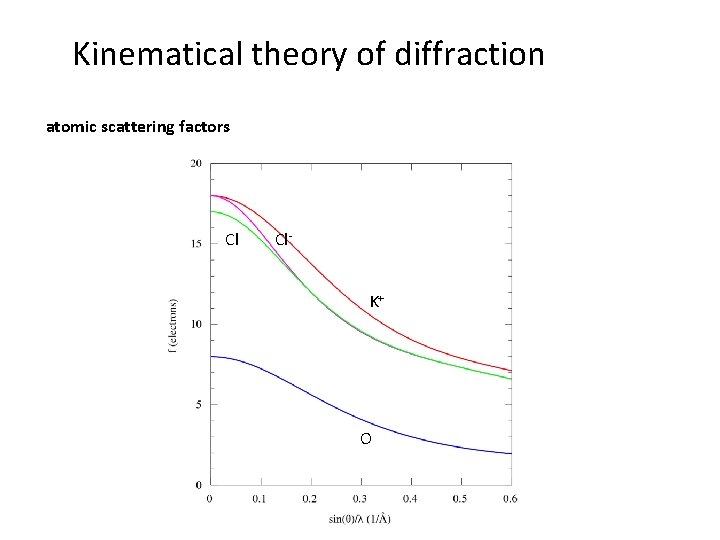
Kinematical theory of diffraction atomic scattering factor - the scattering power of an atom results from the constitution of ist electron shell, which is decribed by the atomic scattering factor - fi are usually tabulated as function of sin q/l - analytical approximation: - ai, bi are c tabulated (calculated by the Hartree-Fock model)

Kinematical theory of diffraction atomic scattering factors Cl Cl. K+ O

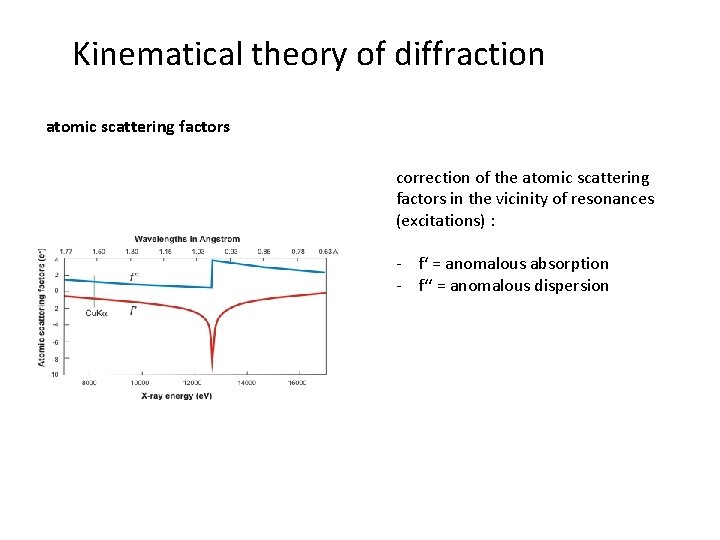
Kinematical theory of diffraction atomic scattering factors correction of the atomic scattering factors in the vicinity of resonances (excitations) : - f‘ = anomalous absorption - f‘‘ = anomalous dispersion

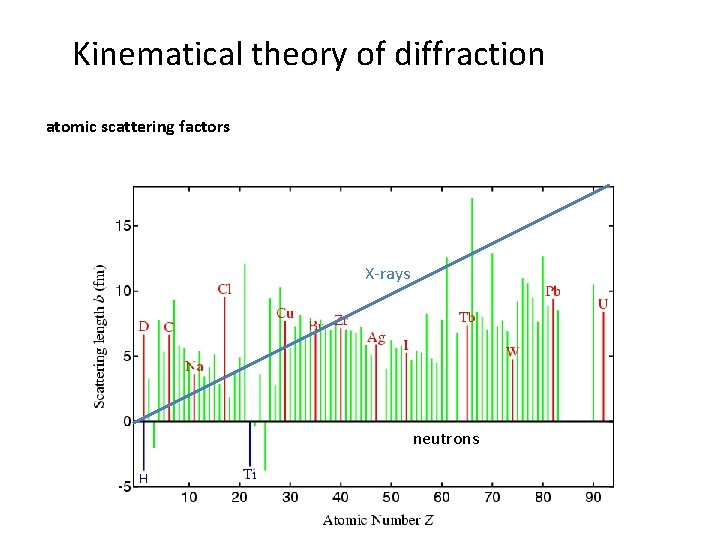
Kinematical theory of diffraction atomic scattering factors X-rays neutrons

Kinematical theory of diffraction periodicity/symmetry of the lattice - Friedel law: diffracted intensities of reciprocal lattice point with positive and negative r* are identical (connected through an inversion centre) incl. symmetry operator from direct space: (real) change of phase, amplitude remains constant structure factors for positive and negative lattice vectors are complex conjugate (imaginary)

Kinematical theory of diffraction periodicity/symetry of the lattice consequences: - point symmetry of an object is kept upon diffraction point group of the diffraction pattern is centrosymmetric = Laue class (also in cases when the point group of the structre is NOT!)

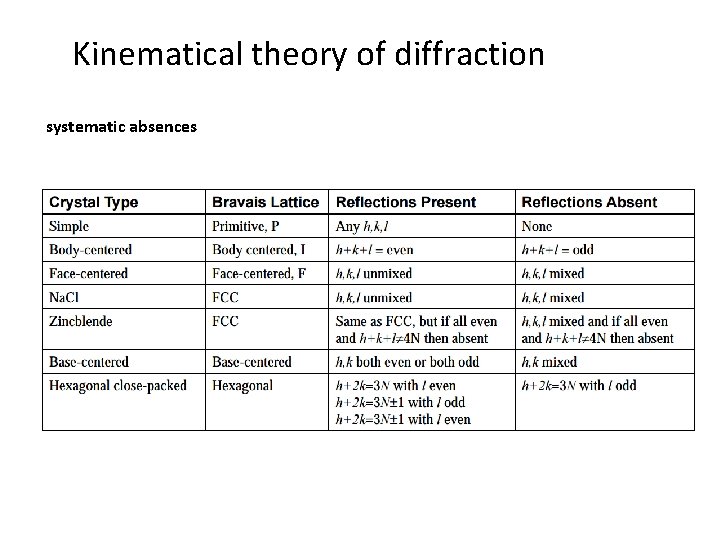
Kinematical theory of diffraction periodicity/symmetry of the lattice consequences: - translation symmetry (centres, screw axes, glide planes) do not impact the symmetry of the diffraction patter, but the systematic absence of certain diffraction maxima goal: interpretation of systematic absences of reflexes in relation to crystal symmetry

Kinematical theory of diffraction systematic absences

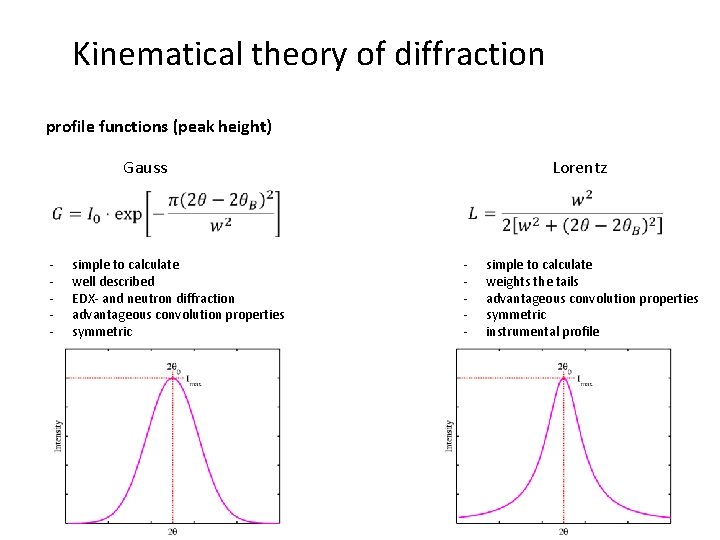
Kinematical theory of diffraction profile functions (peak height) Gauss Lorentz - simple to calculate well described EDX- and neutron diffraction advantageous convolution properties symmetric - simple to calculate weights the tails advantageous convolution properties symmetric instrumental profile

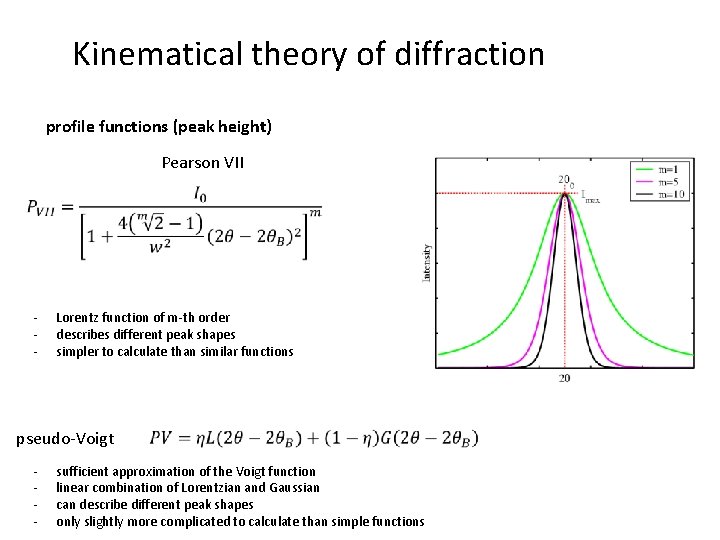
Kinematical theory of diffraction profile functions (peak height) Pearson VII - Lorentz function of m-th order describes different peak shapes simpler to calculate than similar functions pseudo-Voigt - sufficient approximation of the Voigt function linear combination of Lorentzian and Gaussian can describe different peak shapes only slightly more complicated to calculate than simple functions

Kinematical theory of diffraction Debye-Waller factor - Phonons are coupled oscillations of atoms around their equilibrium position - causes a timely variation of the electron density distribution -> variation in scattering power of the atoms - oscillations can assumed to be isotropic (neglection of the next neighbours) - when isotropic, probability density function is a Gaussian - more accurate are anisotropic oscillations (assume ellopsoidal shape) - only at T = 0, atoms should be at rest - timescale of the diffraction experiment >> timescale of atomic oscillations (time average sufficient for description)

Kinematical theory of diffraction