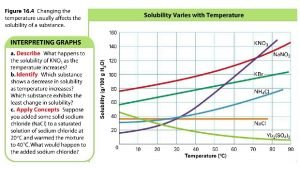
Lattices and Symmetry Scattering and Diffraction Physics Adapted








































- Slides: 80

Lattices and Symmetry Scattering and Diffraction (Physics) (Adapted from: James A. Kaduk IIT Adjunct Faculty, Chemistry) 1

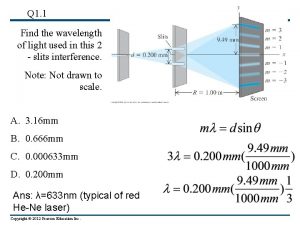
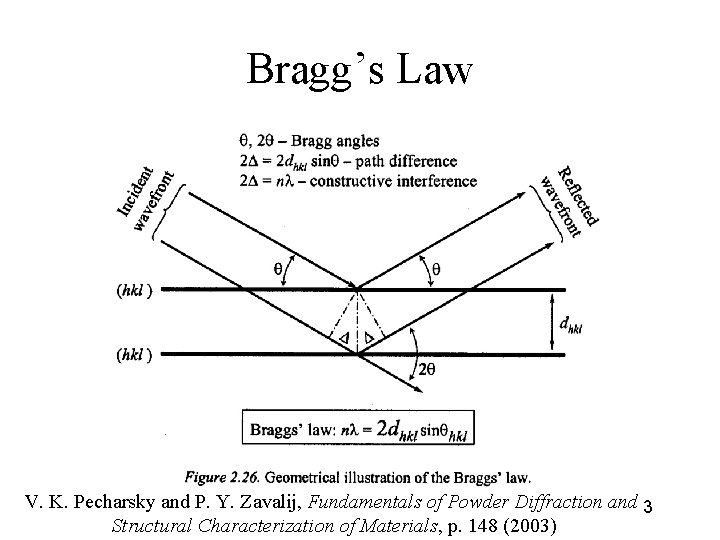
Bragg’s Law Fundamental statement of the way waves scatter off of planes of scatterers n = 2 dsin Rearranging, (1/2 d) = (1/n)sin / We can formulate this so that the n disappears, so that (1/2 d) = sin / 2

Bragg’s Law V. K. Pecharsky and P. Y. Zavalij, Fundamentals of Powder Diffraction and 3 Structural Characterization of Materials, p. 148 (2003)

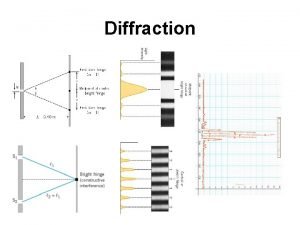
Optical Diffraction PSSC Physics, Figure 18 -A, p. 202 -203 (1965) 4

Optical Diffraction PSSC Physics, Figure 18 -B, p. 202 -203 (1965) 5

Optical Diffraction D. Halliday and R. Resnick, Physics, p. 1124 (1962) 6

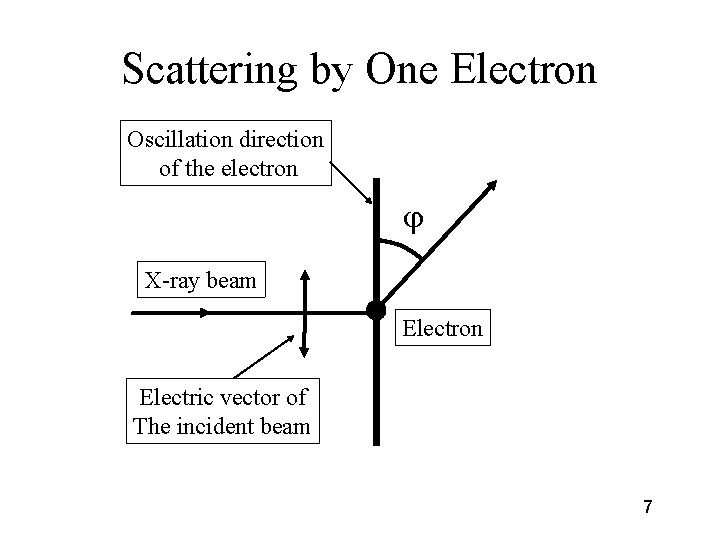
Scattering by One Electron Oscillation direction of the electron X-ray beam Electron Electric vector of The incident beam 7

Electromagnetic Waves E A A z E(t=0; z) = A cos 2 p(z/ ) 8

Consider a new wave displaced by a distance Z from the original wave: E Z new wave z original wave Z corresponds to a phase shift 2π(Z/λ) = α 9

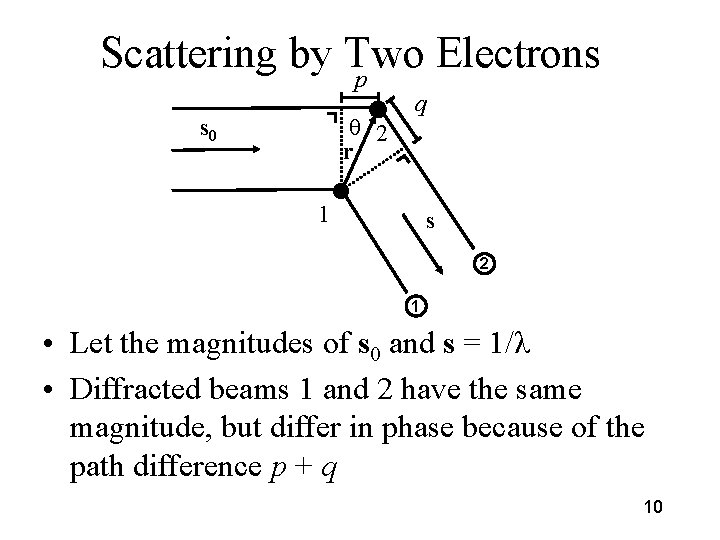
Scattering by Two Electrons p s 0 2 r q 1 s 2 1 • Let the magnitudes of s 0 and s = 1/λ • Diffracted beams 1 and 2 have the same magnitude, but differ in phase because of the path difference p + q 10

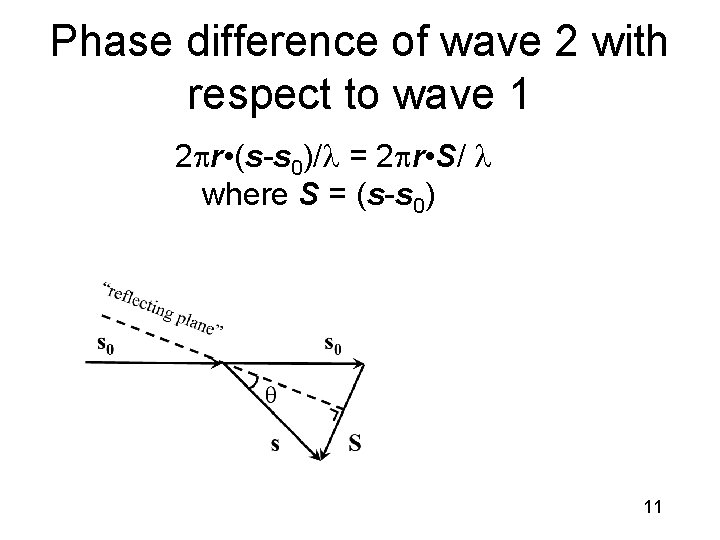
Phase difference of wave 2 with respect to wave 1 2 pr • (s-s 0)/ = 2 pr • S/ where S = (s-s 0) 11

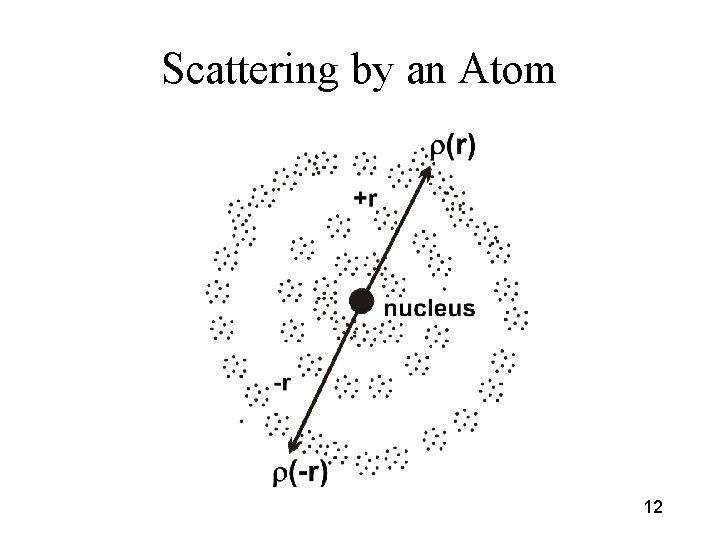
Scattering by an Atom 12

The Atomic Scattering Factor f(S) = ∫ r(r)exp(2 pir • S)d 3 r = 2 ∫ r(r)cos(2 pr • S)d 3 r 13

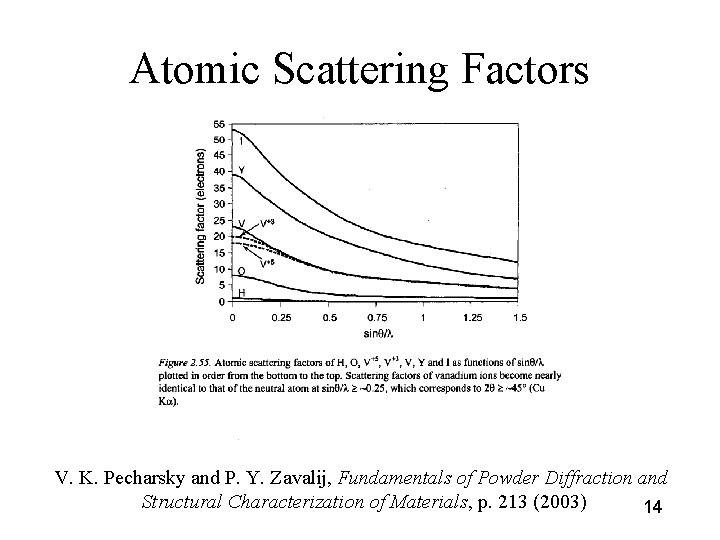
Atomic Scattering Factors V. K. Pecharsky and P. Y. Zavalij, Fundamentals of Powder Diffraction and Structural Characterization of Materials, p. 213 (2003) 14

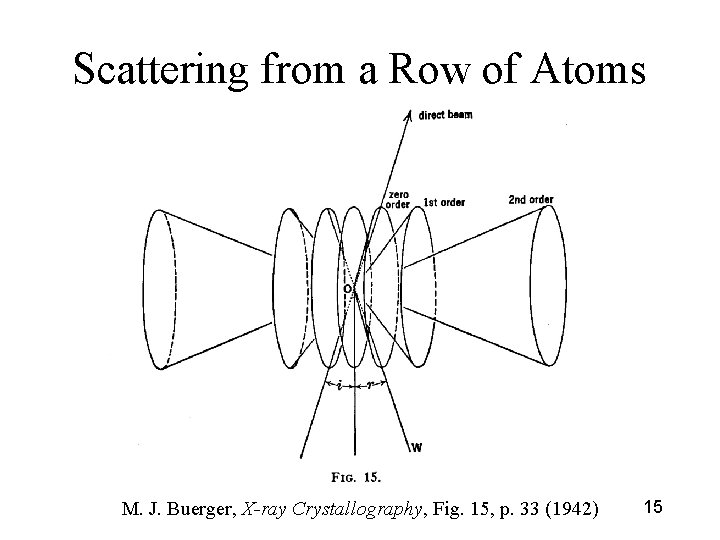
Scattering from a Row of Atoms M. J. Buerger, X-ray Crystallography, Fig. 15, p. 33 (1942) 15

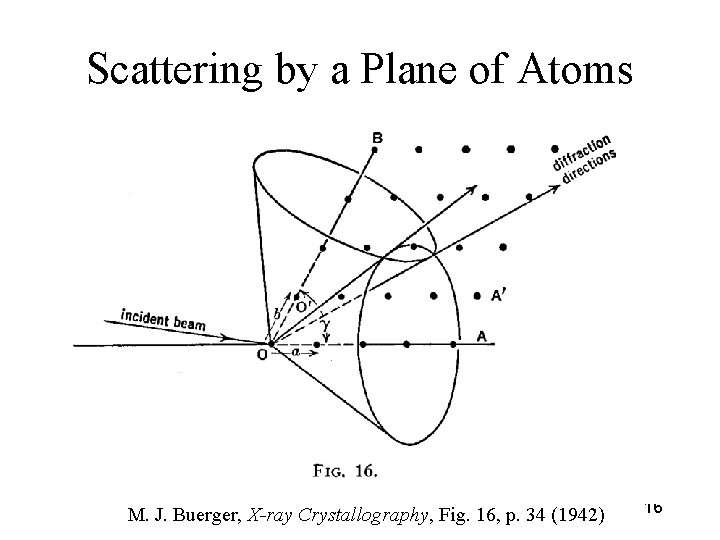
Scattering by a Plane of Atoms M. J. Buerger, X-ray Crystallography, Fig. 16, p. 34 (1942) 16

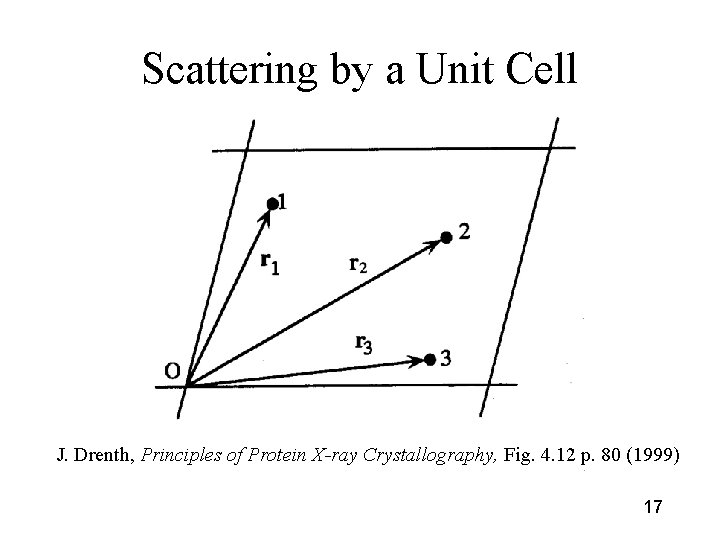
Scattering by a Unit Cell J. Drenth, Principles of Protein X-ray Crystallography, Fig. 4. 12 p. 80 (1999) 17

Scattering by a Unit Cell fj(S) = fjexp(2 pirj • S) for each atom j in the unit cell For the entire ensemble of atoms, F(S) = ∑j=1 n fjexp(2 pirj • S) 18

The crystallographer’s world view Reality can be more complex! 19

Molecules pack together in a regular pattern to form a crystal. There are two aspects to this pattern: Periodicity Symmetry First consider the periodicity… 20

To describe the periodicity, we superimpose (mentally) on the crystal structure a lattice. A lattice is a regular array of geometrical points, each of which has the same environment (they are all equivalent). 21

A Primitive Cubic Lattice (Cs. Cl) 22

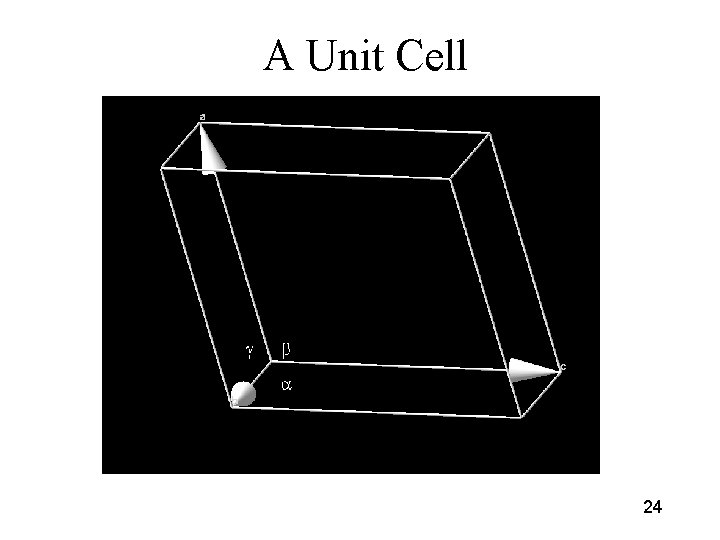
A unit cell of a lattice (or crystal) is a volume which can describe the lattice using only translations. In 3 dimensions (for crystallographers), this volume is a parallelepiped. Such a volume can be defined by six numbers – the lengths of the three sides, and the angles between them – or three basis vectors. 23

A Unit Cell 24

Descriptions of the Unit Cell a, b, c, , , a, b, c x 1 a + x 2 b + x 3 c, 0 xn < 1 lattice points = ha + kb + lc, hkl integers domain of influence – Dirichlet domain, Voronoi domain, Wigner-Seitz cell, Brillouin zone 25

26

The Reduced Cell • 3 shortest non-coplanar translations • Main Conditions (shortest vectors) • Special Conditions (unique) • May not exhibit the true symmetry 27

28

Point Symmetry Elements • A point symmetry operation does not alter at least one point upon which it operates – Rotation axes – Mirror planes – Rotation-inversion axes (rotation-reflection) – Center Screw axes and glide planes are not point symmetry elements! 29

Symmetry Operations • A proper symmetry operation does not invert the handedness of a chiral object – Rotation – Screw axis – Translation • An improper symmetry operation inverts the handedness of a chiral object – – Reflection Inversion Glide plane Rotation-inversion 30

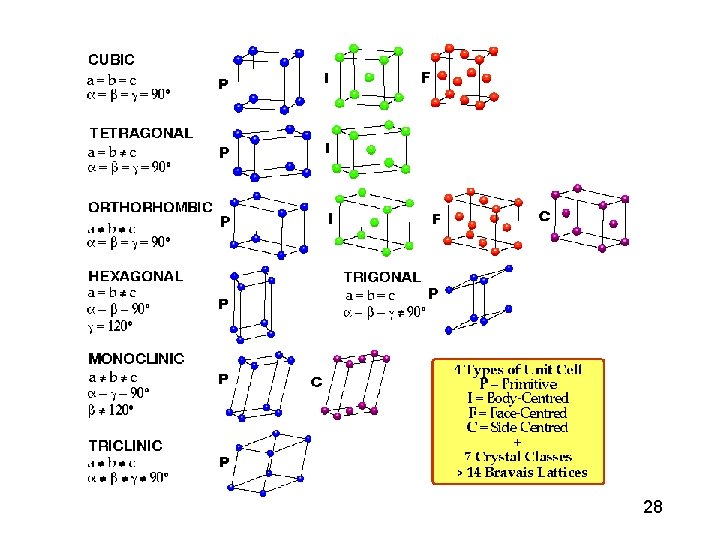
Not all combinations of symmetry elements are possible. In addition, some point symmetry elements are not possible if there is to be translational symmetry as well. There are only 32 crystallographic point groups consistent with periodicity in three dimensions. 31

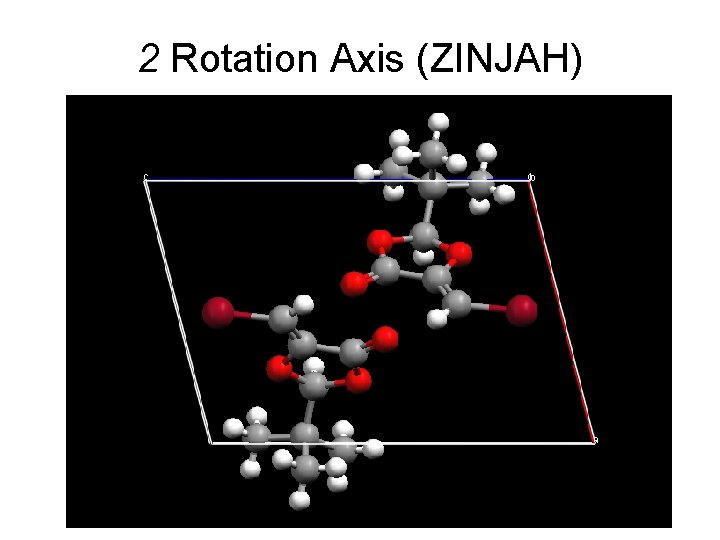
2 Rotation Axis (ZINJAH) 32

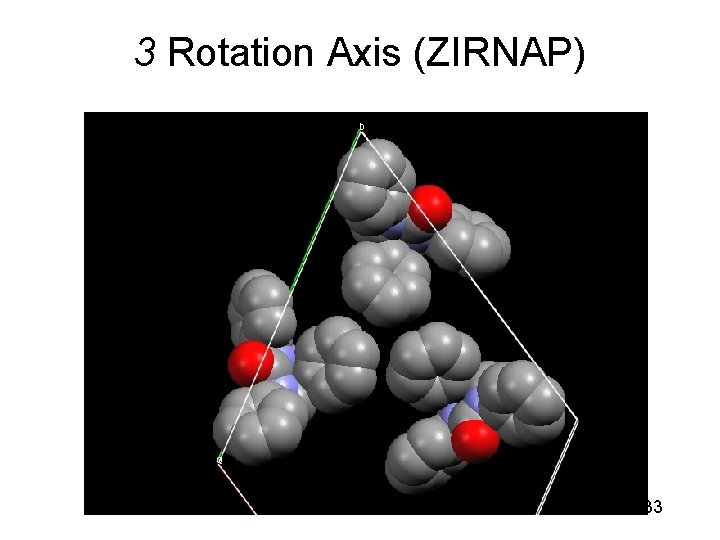
3 Rotation Axis (ZIRNAP) 33

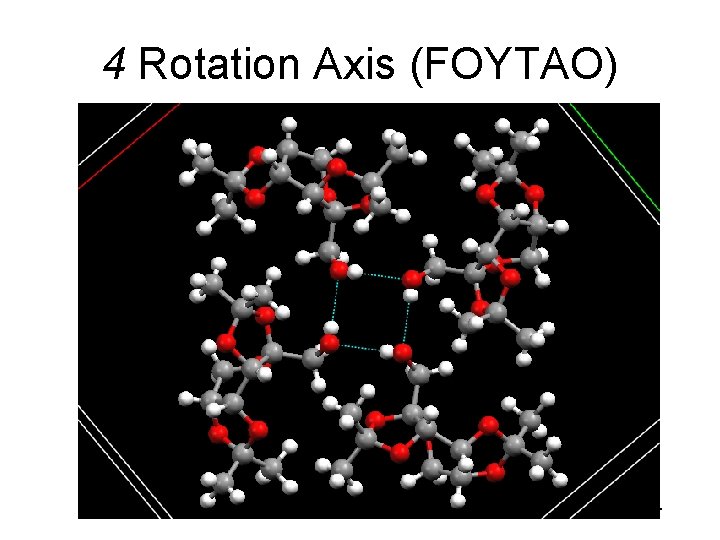
4 Rotation Axis (FOYTAO) 34

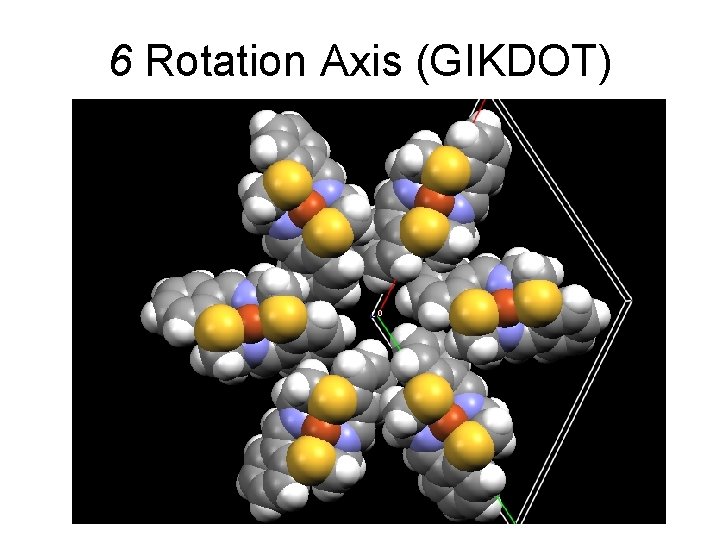
6 Rotation Axis (GIKDOT) 35

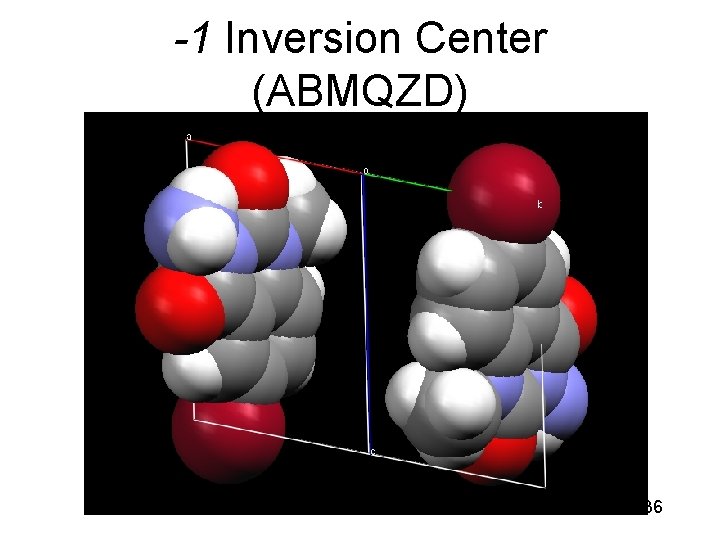
-1 Inversion Center (ABMQZD) 36

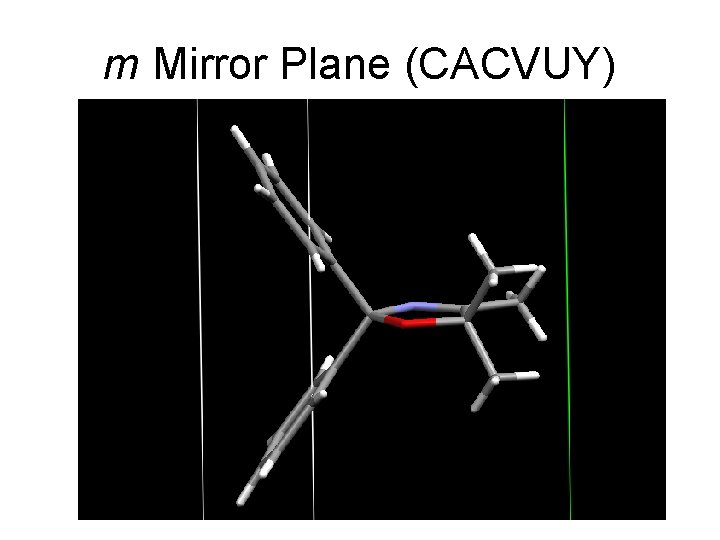
m Mirror Plane (CACVUY) 37

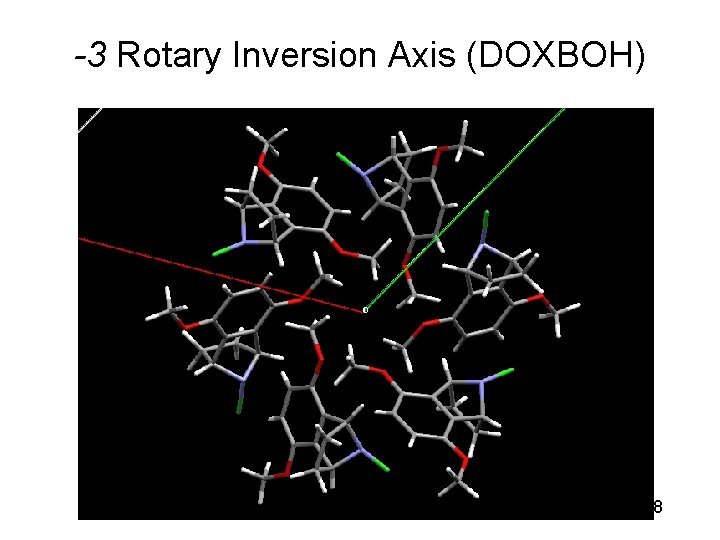
-3 Rotary Inversion Axis (DOXBOH) 38

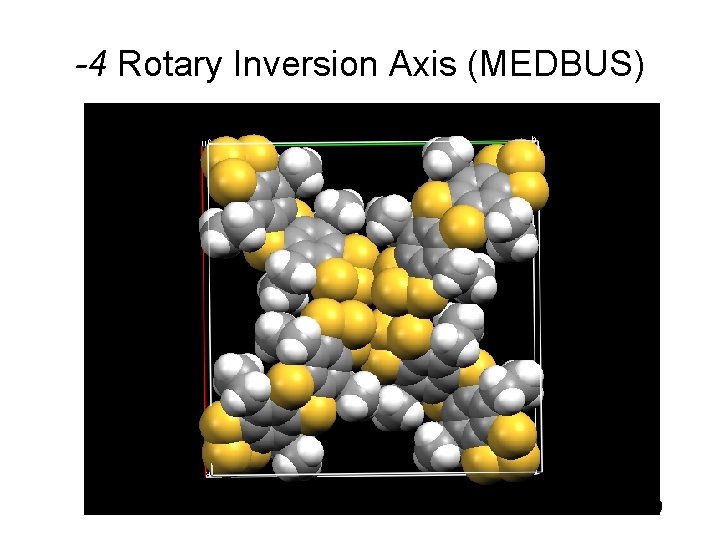
-4 Rotary Inversion Axis (MEDBUS) 39

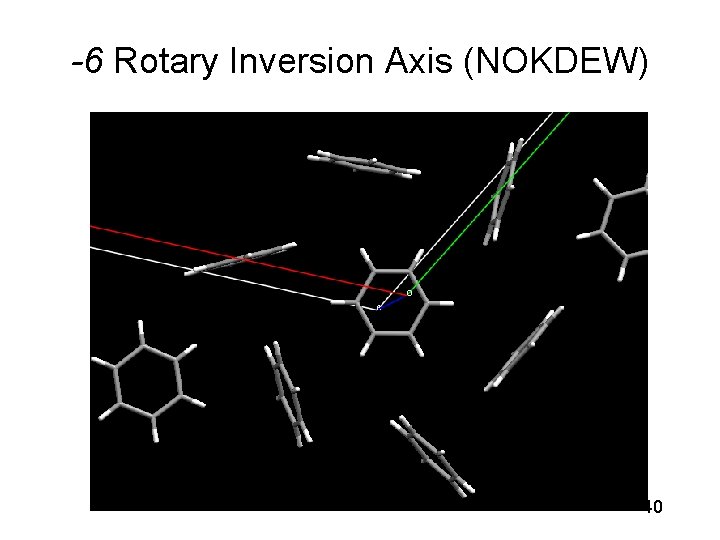
-6 Rotary Inversion Axis (NOKDEW) 40

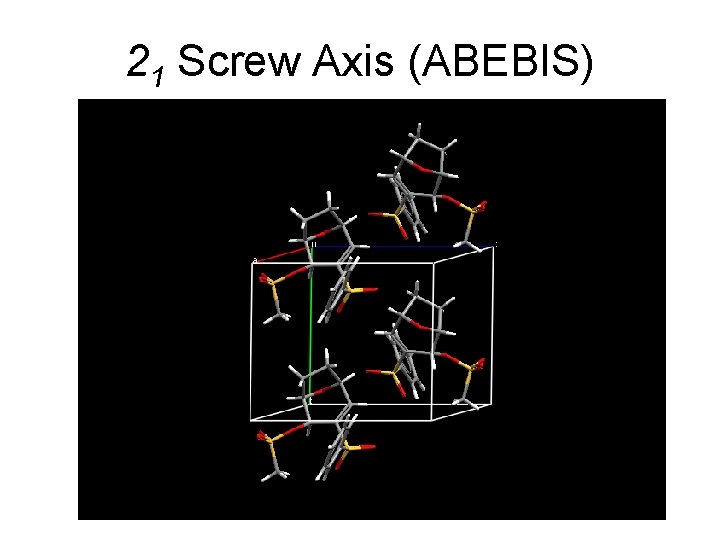
21 Screw Axis (ABEBIS) 41

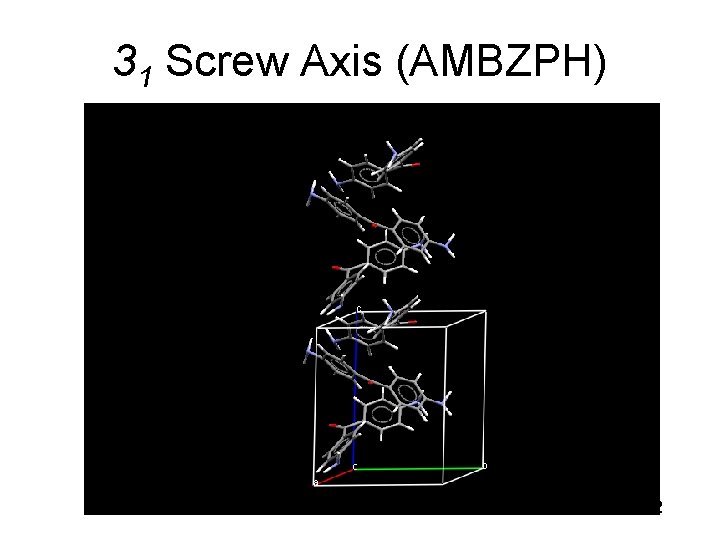
31 Screw Axis (AMBZPH) 42

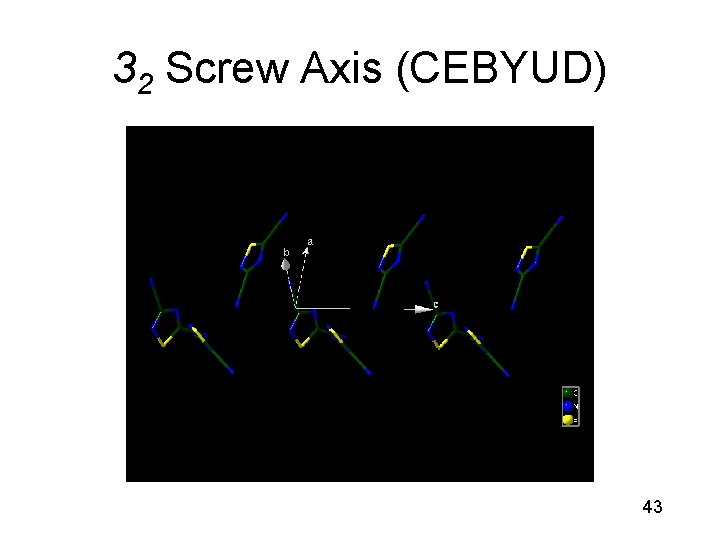
32 Screw Axis (CEBYUD) 43

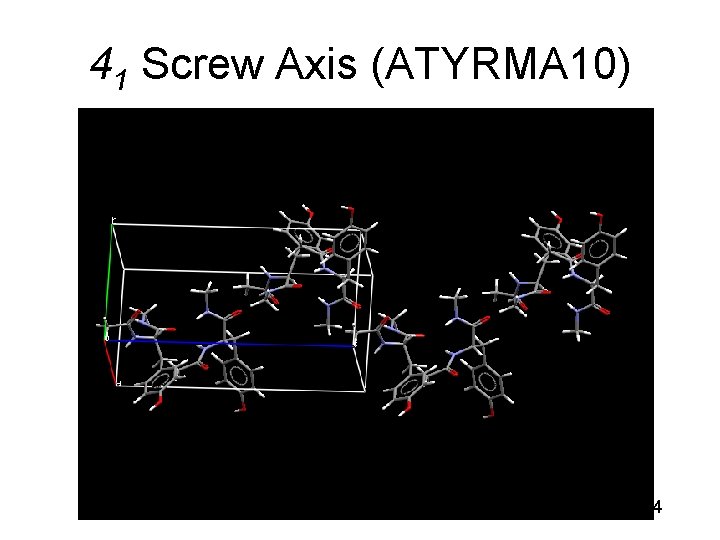
41 Screw Axis (ATYRMA 10) 44

42 Screw Axis (HYDTML) 45

43 Screw Axis (PIHCAK) 46

61 Screw Axis (DOTREJ) 47

62 Screw Axis (BHPETS 10) 48

63 Screw Axis (NAIACE) 49

64 Screw Axis (TOXQUS) 50

65 Screw Axis (BEHPEJ) 51

c Glide (ABOPOW) 52

n Glide (BOLZIL) 53

d (diamond) Glide (FURHUV) 54

Not all space groups are possible for protein crystals, because the chirality of the building blocks requires that the assembled molecule be chiral. 55

56

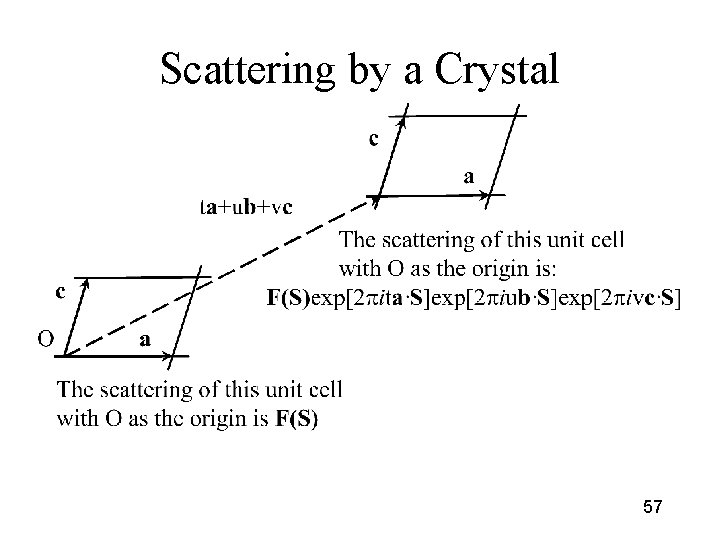
Scattering by a Crystal 57

Total scattering by a crystal For a unit cell with its own origin at ta + ub + vc the scattering is F(S) e 2 pita • Se 2 piub • Se 2 pivc • S and the total scattering by the crystal is K(S) = F(S) ∑t=0 n 1 e 2 pita • S ∑u=0 n 2 e 2 piub • S ∑v=0 n 3 e 2 pivc • S 58

Fourier Transform The Fourier transform is an equation to calculate the frequency, amplitude and phase of each sine wave needed to make up any given signal x(t): F(f) = ∫+x(t)ei 2 pftdt 59

Brightness image / Fourier transform http: //cns-alumni. bu. edu/~slehar/fourier. html 60

Kevin Cowtan’s Fourier Duck http: //www. ysbl. york. ac. uk/~cowtan/fourier/magic. html 61

Kevin Cowtan’s Fourier Cat http: //www. ysbl. york. ac. uk/~cowtan/fourier/magic. html 62

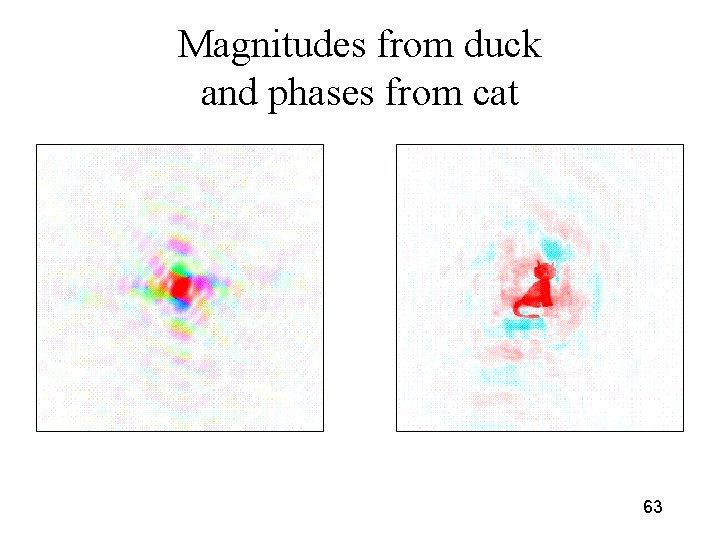
Magnitudes from duck and phases from cat 63

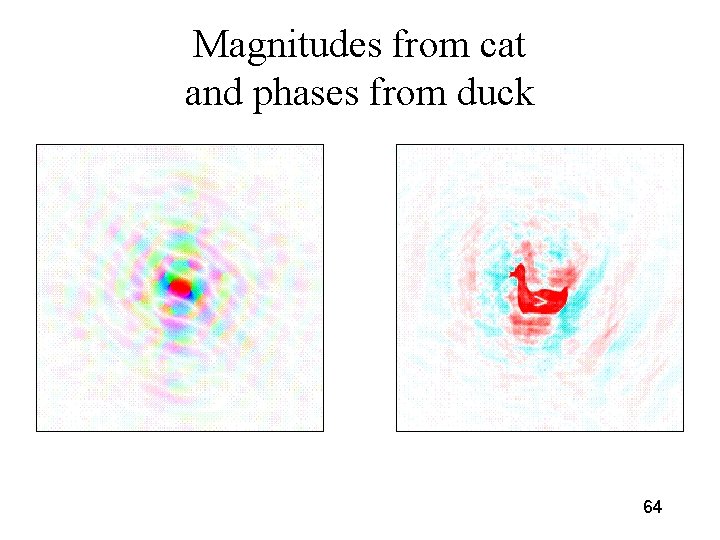
Magnitudes from cat and phases from duck 64

A tail of two cats http: //www. ysbl. york. ac. uk/~cowtan/fourier/coeff. html Magnitudes only 65

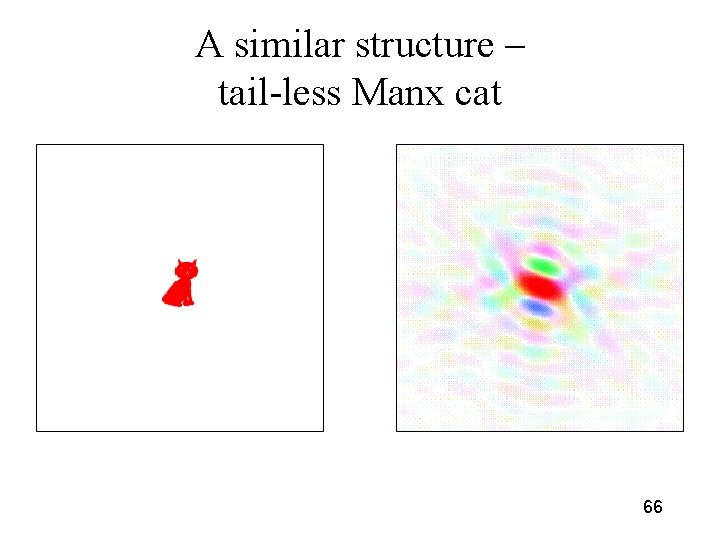
A similar structure – tail-less Manx cat 66

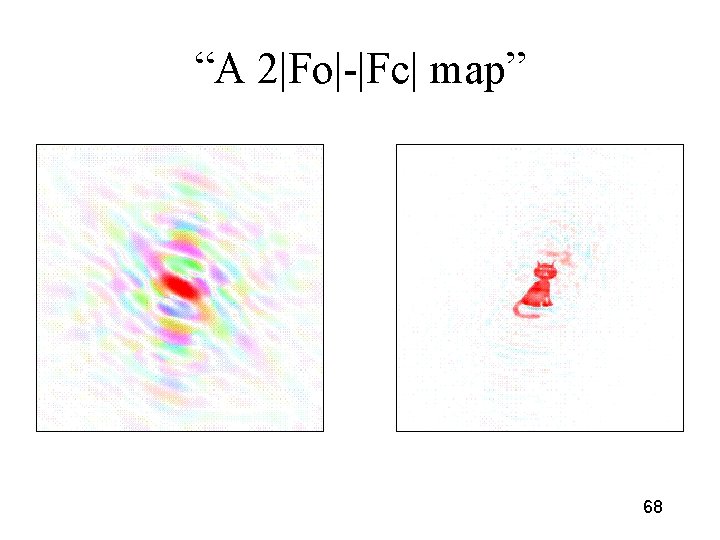
Known magnitudes and Manx phases “an |Fo| map” Despite the fact that the phases contain more structural information about the image than the magnitudes, the missing tail is restored at about half of its original weight. This occurs only when the phases are almost correct. The factor of one half arises because we are making the right correction parallel to the estimated phase, but no correction perpendicular to the phase (and <cos 2>=1/2). There is also some noise in the image. 67

“A 2|Fo|-|Fc| map” 68

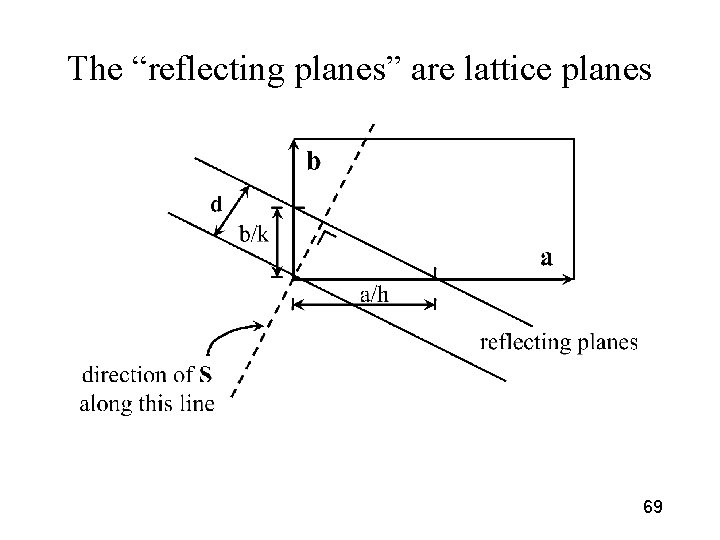
The “reflecting planes” are lattice planes 69

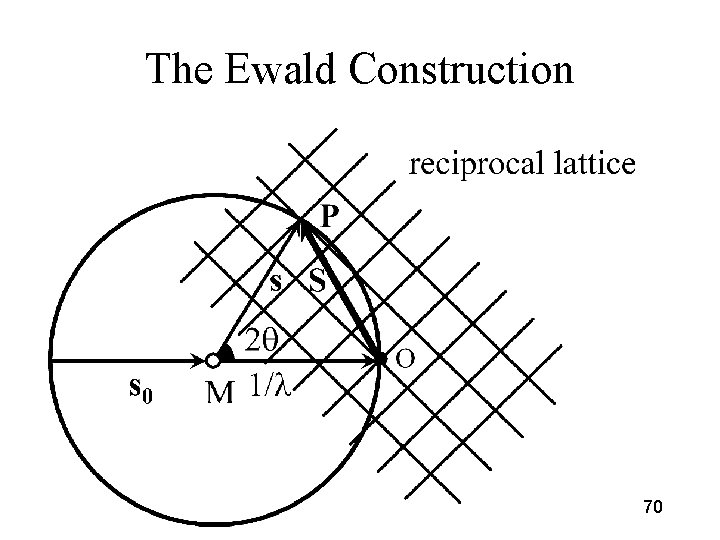
The Ewald Construction 70

Mosaicity (Mosaic Spread) B. D. Cullity and S. R. Stock, Elements of X-ray Diffraction, p. 175 (2001). 71

The Patterson Function Let P(u, v, w) = P(u) = (1/V)∑h |F(h)|2 cos(2 ph • u) Or (if there is no anomalous dispersion) P(u) = (1/V)∑h |F(h)|2 e 2 pih • u 72

What does the Patterson function mean? Consider an alternate expression P(u) = ∫r r(r)r(r+u)dvreal This shows that the Patterson function is actually a type of correlation function of the electron density with itself, or, to put it another way, it’s a convolution of the electron density with its inverse. 73

More about Structure Factors F(S) = ∑j=1 n fje 2 pirj • S For noncentrosymmetric structures, the following reformulation may be useful: F(S) = ∑j=1 n fjcos(2 pirj • S) + i ∑j=1 n fjsin(2 pirj • S) = A(S) + i. B(S) 74

Falloff in intensity with resolution The falloff makes statistical analysis awkward. Intensities are normally measured on an arbitrary scale. For large numbers of welldistributed S <|F(S)|2> = <I(abs, S)> = ∑ifi 2 But we estimate fi 2 as 2 / 2 2 0 2 2 B sin fi = (fi ) e i Where Bi is a measure of the mobility of atom i. 75

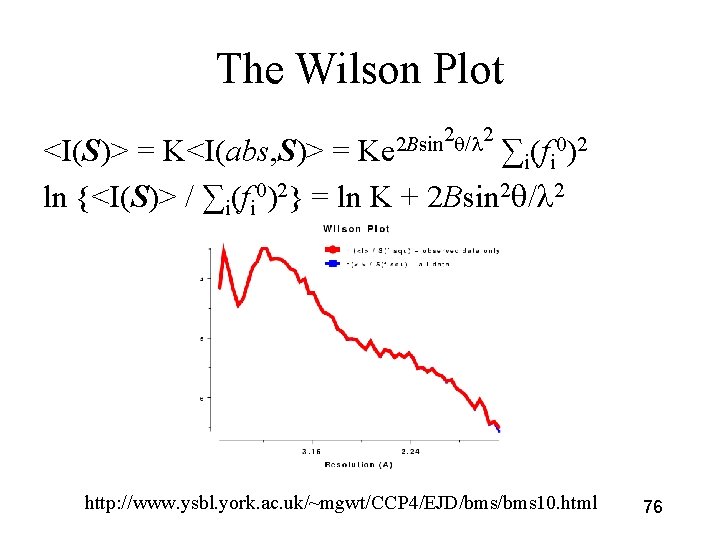
The Wilson Plot 2 / 2 2 Bsin Ke <I(S)> = K<I(abs, S)> = ∑i(fi 0)2 ln {<I(S)> / ∑i(fi 0)2} = ln K + 2 Bsin 2 / 2 http: //www. ysbl. york. ac. uk/~mgwt/CCP 4/EJD/bms 10. html 76

Normalized Structure Factors 77

Least Squares Refinement • Assume observations are uncorrelated • If Error distributions are Gaussian Observations are weighted by 1/ 2 LS gives maximum likelihood estimates of xj • Restraints count as observations (weights? ) E. Prince, Mathematical Techniques in Crystallography and Materials Science, Springer-Verlag (1994) 78

Accuracy vs. Precision • The standard uncertainty (esd) is a measure of precision • LS yields minimum variances • Correlations • Systematic errors • Accuracy? International Tables for Crystallography, Volume F, Section 18. 5 79

The Macromolecular CIF Dictionary (mm. CIF) International Tables for Crystallography, Volume G Section 4. 5 pages 295 -443 (!) 80
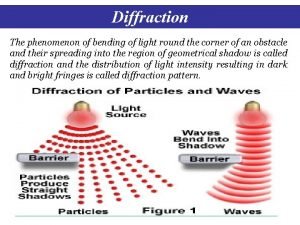
 Diffraction and scattering
Diffraction and scattering Scattering cross section in nuclear physics
Scattering cross section in nuclear physics 7 crystal systems and 14 bravais lattices
7 crystal systems and 14 bravais lattices Motif and lattice
Motif and lattice Lattices and boolean algebra
Lattices and boolean algebra Bravais lattices
Bravais lattices Bravais lattice
Bravais lattice Bravais lattices
Bravais lattices Bravais lattices
Bravais lattices Electrostatic attraction
Electrostatic attraction Empty lattice
Empty lattice 14 bravais lattices
14 bravais lattices Oded regev lattices
Oded regev lattices Oded regev lattices
Oded regev lattices Properties of ionic lattices
Properties of ionic lattices Lattices definition
Lattices definition Ppt on symmetry
Ppt on symmetry This passage is adapted from jane austen
This passage is adapted from jane austen How are red blood cells adapted
How are red blood cells adapted Adapted with permission from
Adapted with permission from In what ways have the highland maya adapted to modern life?
In what ways have the highland maya adapted to modern life? Xerophytic plants diagram
Xerophytic plants diagram Climate of the chaparral biome
Climate of the chaparral biome 5 adaptive features of camel
5 adaptive features of camel Adapted animals in the rainforest
Adapted animals in the rainforest The two brothers adapted
The two brothers adapted Adapted from the internet
Adapted from the internet How is amoeba adapted for gas exchange bbc bitesize
How is amoeba adapted for gas exchange bbc bitesize How have plants adapted to the rainforest
How have plants adapted to the rainforest Spermopsida as successful land plants
Spermopsida as successful land plants The outsiders adapted for struggling readers
The outsiders adapted for struggling readers Differ synoynm
Differ synoynm How are giraffes long necks adapted to their lifestyle
How are giraffes long necks adapted to their lifestyle Symmetric with respect to
Symmetric with respect to Rayleigh theory of light scattering
Rayleigh theory of light scattering Fraunhofer and fresnel diffraction
Fraunhofer and fresnel diffraction Diffraction by circular aperature
Diffraction by circular aperature Diffraction and polarization
Diffraction and polarization Blue relfection ray
Blue relfection ray Diffraction through single slits derivation
Diffraction through single slits derivation Principal maxima and secondary maxima
Principal maxima and secondary maxima Bragg's diffraction condition in reciprocal lattice
Bragg's diffraction condition in reciprocal lattice Zimm plot excel
Zimm plot excel Scattering of light in suspension
Scattering of light in suspension Scattering in central force field
Scattering in central force field Rayleigh vs mie
Rayleigh vs mie Rayleigh vs raman scattering
Rayleigh vs raman scattering Photodesintegration
Photodesintegration Reciprocal network
Reciprocal network Liquid crystal display
Liquid crystal display Scattering reaction
Scattering reaction Photoelectric and compton effect
Photoelectric and compton effect Polarisation by scattering
Polarisation by scattering Conservation of momentum
Conservation of momentum Scattering matrix for a reciprocal network is
Scattering matrix for a reciprocal network is Coherence and incoherence
Coherence and incoherence Double scattering
Double scattering Pemantulan dan pembiasan gelombang elektromagnetik
Pemantulan dan pembiasan gelombang elektromagnetik Raman scattering definition
Raman scattering definition Coherent scattering
Coherent scattering Dynamic light scattering 원리
Dynamic light scattering 원리 Mie plot
Mie plot Non elastic scattering
Non elastic scattering Rutherford scattering
Rutherford scattering Rayleigh theory of light scattering
Rayleigh theory of light scattering Scattering matrix
Scattering matrix Pauli blocking of light scattering in degenerate fermions
Pauli blocking of light scattering in degenerate fermions Scattering matrix
Scattering matrix Double parton scattering
Double parton scattering Scattering efficiency
Scattering efficiency Scattering matrix
Scattering matrix Scattering of light
Scattering of light Diffusione thomson
Diffusione thomson Phase doppler anemometry
Phase doppler anemometry Golite trig 2
Golite trig 2 Photoelectric effect graph explanation
Photoelectric effect graph explanation Medium energy ion scattering
Medium energy ion scattering Compton scattering
Compton scattering Light scattering
Light scattering Rayleigh scattering formula
Rayleigh scattering formula Rayleigh scattering intensity formula
Rayleigh scattering intensity formula