Lattices and Symmetry Scattering and Diffraction Physics James

Lattices and Symmetry Scattering and Diffraction (Physics) James A. Kaduk INEOS Technologies Analytical Science Research Services Naperville IL 60566 James. Kaduk@innovene. com 1

Harry Potter and the Sorcerer’s (Philosopher’s) Stone Ron: Seeker? But first years never make the house team. You must be the youngest Quiddich player in … Harry: … a century. According to Mc. Gonagall. Fred/George: Well done, Harry. Wood’s just told us. Ron: Fred and George are on the team, too. Beaters. Fred/George: Our job is to make sure you don’t get bloodied up too bad. 2

Alastor “Mad-Eye” Moody – “Constant Vigilance” Harry Potter and the Goblet of Fire (2005) 3

The crystallographer’s world view Reality can be more complex! 4

Twinning at the atomic level International Tables for Crystallography, Volume D, p. 438 5

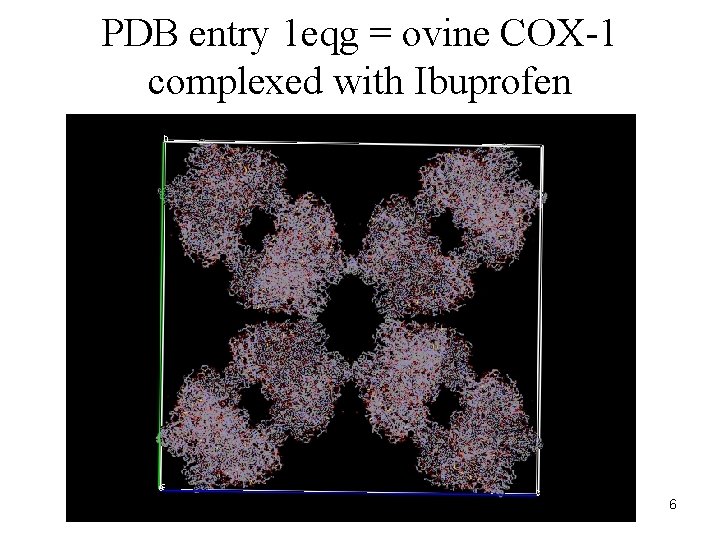
PDB entry 1 eqg = ovine COX-1 complexed with Ibuprofen 6

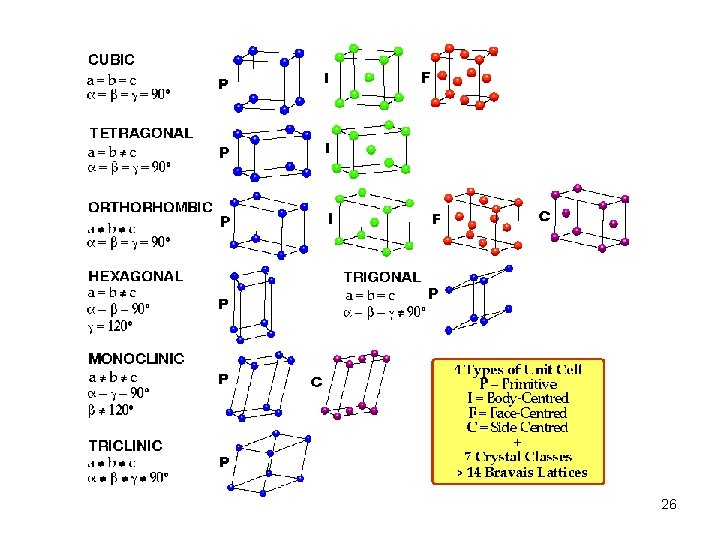
Atoms (molecules) pack together in a regular pattern to form a crystal. There are two aspects to this pattern: Periodicity Symmetry First, consider the periodicity… 7

To describe the periodicity, we superimpose (mentally) on the crystal structure a lattice. A lattice is a regular array of geometrical points, each of which has the same environment (they are all equivalent). 8

A Primitive Cubic Lattice (Cs. Cl) 9

A unit cell of a lattice (or crystal) is a volume which can describe the lattice using only translations. In 3 dimensions (for crystallographers), this volume is a parallelepiped. Such a volume can be defined by six numbers – the lengths of the three sides, and the angles between them – or three basis vectors. 10

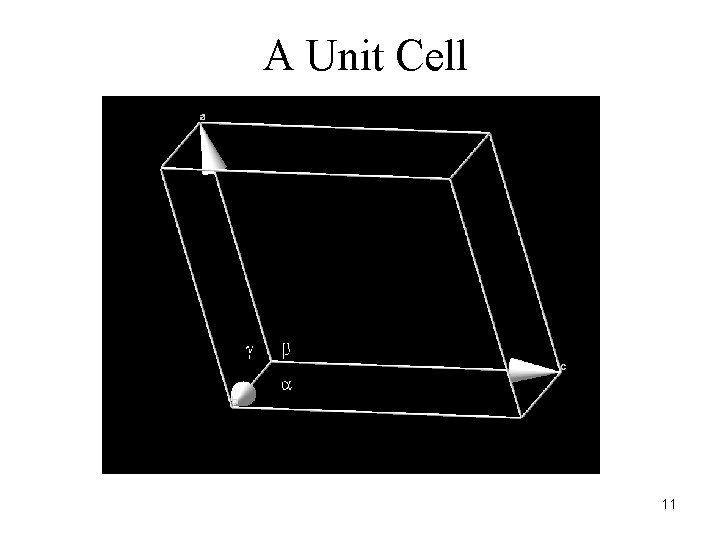
A Unit Cell 11

Descriptions of the Unit Cell a, b, c, , , a, b, c x 1 a + x 2 b + x 3 c, 0 xn < 1 lattice points = ha + kb + lc, hkl integers domain of influence – Dirichlet domain, Voronoi domain, Wigner-Seitz cell, Brillouin zone 12

A Brillouin Zone C. Kittel, Introduction to Solid State Physics, 6 th Edition, p. 41 (1986) 13

The unit cell is not unique (c: My. FilesClinicindex 2. wrl) 14

15

16

17

How do I pick the unit cell? • Axis system (basis set) is right-handed • Symmetry defines natural directions and boundaries • Angles close to 90° • Standard settings of space groups • To make structural similarities clearer 18

The Reduced Cell • 3 shortest non-coplanar translations • Main Conditions (shortest vectors) • Special Conditions (unique) • May not exhibit the true symmetry 19

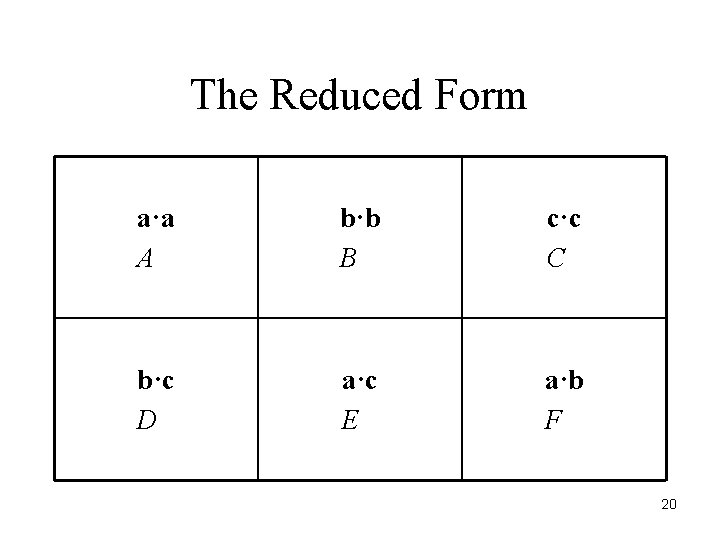
The Reduced Form a·a A b·b B c·c C b·c D a·c E a·b F 20

Positive Reduced Form, Type I Cell, all angles < 90°, T = (a·b)(b·c)(c·a) > 0 Main conditions: a·a b·b c·c a·c ½ a·a Special conditions: if a·a = b·b then if b·b = c·c then if b·c = ½ b·b then if a·c = ½ a·a then if a·b = ½ a·a then b·c ½ b·b a·b ½ a·a b·c a·c a·b 2 a·c a·b 2 b·c a·c 2 b·c 21

Negative reduced Form, Type II Cell angles 90°, T = (a·b)(b·c)(c·a) ≤ 0 Main Conditions: a·a b·b c·c b·c| ½ b·b |a·c| ½ a·a |a·b| a·a ( |b·c| + |a·b| ) ½ ( a·a + b·b ) Special Conditions: if a·a = b·b then |b·c| |a·c| if b·b = c·c then |a·c| |a·b| if |b·c| = ½ b·b then a·b = 0 if |a·c| = ½ a·a then a·b = 0 if |a·b| = ½ a·a then a·c = 0 if ( |b·c| + |a·b| ) = ½ ( a·a + b·b ) then a·a 2 |a·c| + |a·b| 22

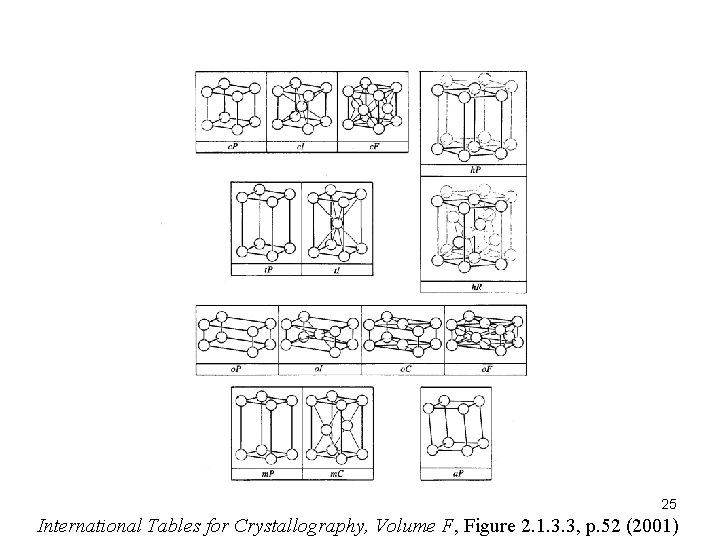
There are 44 reduced forms. The relationships among the six terms determine the Bravais lattice of the crystal. J. K. Stalick and A. D. Mighell, NBS Technical Note 1229, 1986. A. D. Mighell and J. R. Rodgers, Acta Cryst. , A 36, 321 -326 (1980). 23

“The Normalized Reduced Form and Cell: Mathematical Tools for Lattice Analysis – Symmetry and Similarity”, Alan D. Mighell, J. Res. Nat. Inst. Stand. Tech. , 108(6), 447 -452 (2003). 24

25 International Tables for Crystallography, Volume F, Figure 2. 1. 3. 3, p. 52 (2001)

26

“The mystery of the fifteenth Bravais lattice”, A. Nussbaum, Amer. J. Phys. , 68(10), 950 -954 (2000). http: //ojps. aip. org/ajp/ 27

Symmetry Groups and Their Applications, W. Miller, Jr. , Academic Press, New York (1972), Chapter 2. 28

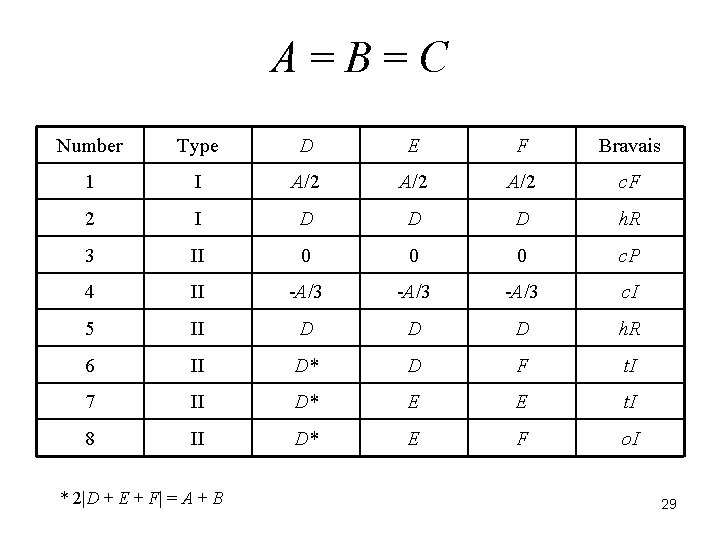
A=B=C Number Type D E F Bravais 1 I A/2 A/2 c. F 2 I D D D h. R 3 II 0 0 0 c. P 4 II -A/3 c. I 5 II D D D h. R 6 II D* D F t. I 7 II D* E E t. I 8 II D* E F o. I * 2|D + E + F| = A + B 29

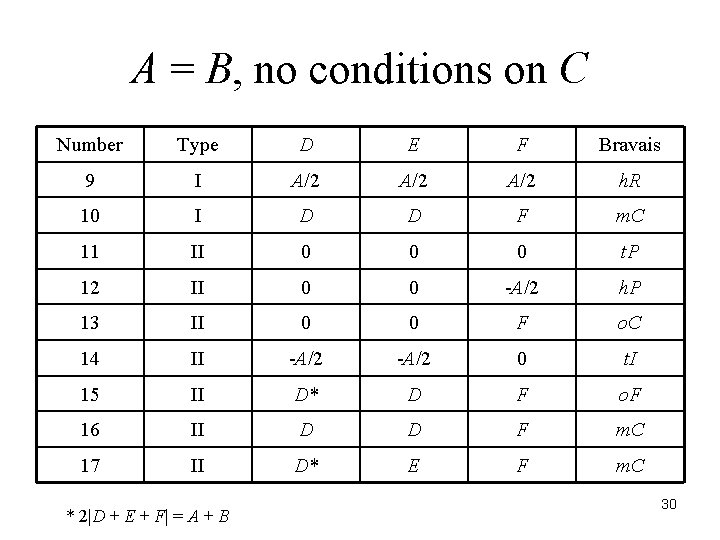
A = B, no conditions on C Number Type D E F Bravais 9 I A/2 A/2 h. R 10 I D D F m. C 11 II 0 0 0 t. P 12 II 0 0 -A/2 h. P 13 II 0 0 F o. C 14 II -A/2 0 t. I 15 II D* D F o. F 16 II D D F m. C 17 II D* E F m. C * 2|D + E + F| = A + B 30

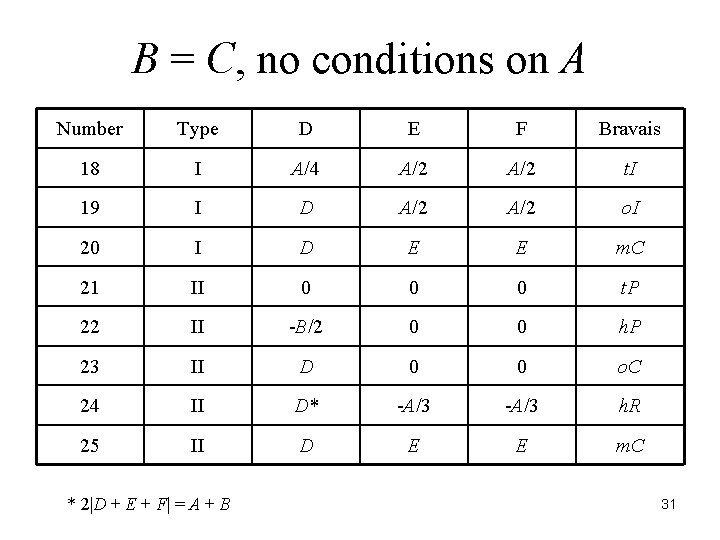
B = C, no conditions on A Number Type D E F Bravais 18 I A/4 A/2 t. I 19 I D A/2 o. I 20 I D E E m. C 21 II 0 0 0 t. P 22 II -B/2 0 0 h. P 23 II D 0 0 o. C 24 II D* -A/3 h. R 25 II D E E m. C * 2|D + E + F| = A + B 31

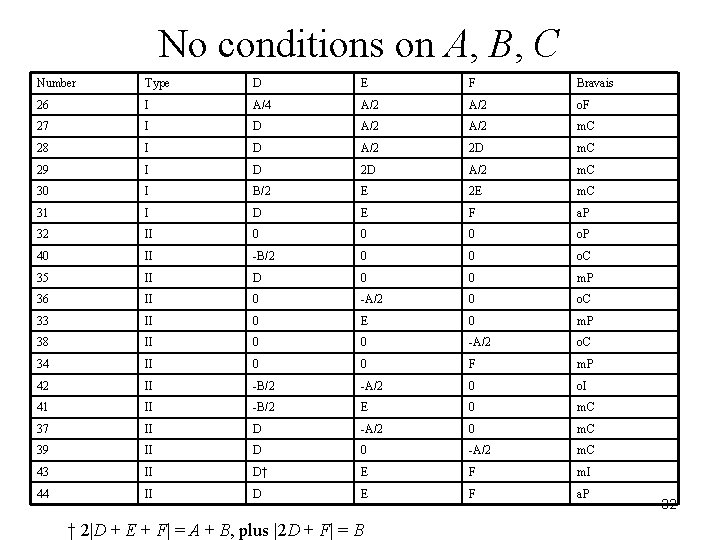
No conditions on A, B, C Number Type D E F Bravais 26 I A/4 A/2 o. F 27 I D A/2 m. C 28 I D A/2 2 D m. C 29 I D 2 D A/2 m. C 30 I B/2 E 2 E m. C 31 I D E F a. P 32 II 0 0 0 o. P 40 II -B/2 0 0 o. C 35 II D 0 0 m. P 36 II 0 -A/2 0 o. C 33 II 0 E 0 m. P 38 II 0 0 -A/2 o. C 34 II 0 0 F m. P 42 II -B/2 -A/2 0 o. I 41 II -B/2 E 0 m. C 37 II D -A/2 0 m. C 39 II D 0 -A/2 m. C 43 II D† E F m. I 44 II D E F a. P † 2|D + E + F| = A + B, plus |2 D + F| = B 32

Indexing programs can get “caught” in a reduced cell, and miss the (higher) true symmetry. It’s always worth a manual check of your cell. 33

The metric symmetry can be higher than the crystallographic symmetry! (A monoclinic cell can have β = 90°) 34

http: //www. haverford. edu/physics-astro/songs/bravais. htm 35

Definitions [hkl] <hkl> (hkl) {hkl} hkl indices of a lattice direction indices of a set of symmetryequivalent lattice directions indices of a single crystal face indices of a set of all symmetryequivalent crystal faces indices of a Bragg reflection 36

Now consider the symmetry… 37

Point Symmetry Elements • A point symmetry operation does not alter at least one point upon which it operates – Rotation axes – Mirror planes – Rotation-inversion axes (rotation-reflection) – Center Screw axes and glide planes are not point symmetry elements! 38

Symmetry Operations • A proper symmetry operation does not invert the handedness of a chiral object – Rotation – Screw axis – Translation • An improper symmetry operation inverts the handedness of a chiral object – – Reflection Inversion Glide plane Rotation-inversion 39

Not all combinations of symmetry elements are possible. In addition, some point symmetry elements are not possible if there is to be translational symmetry as well. There are only 32 crystallographic point groups consistent with periodicity in three dimensions. 40

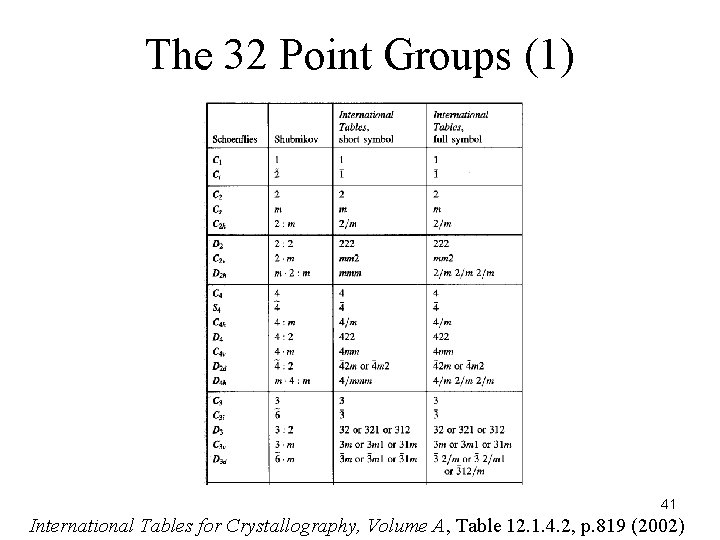
The 32 Point Groups (1) 41 International Tables for Crystallography, Volume A, Table 12. 1. 4. 2, p. 819 (2002)

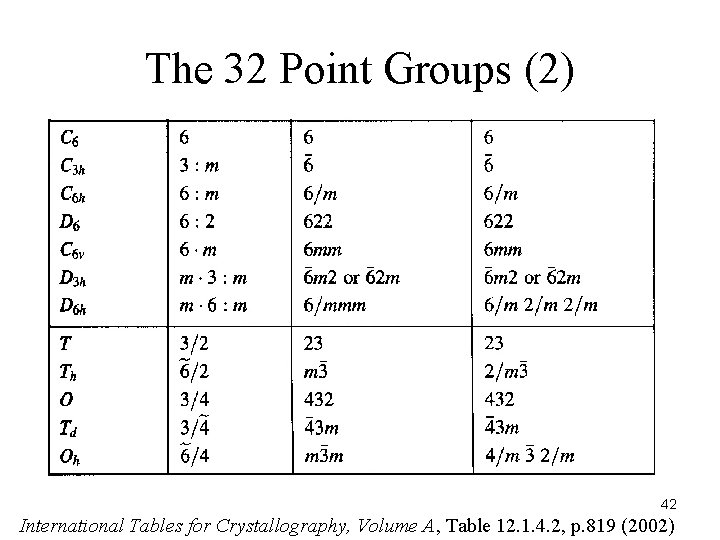
The 32 Point Groups (2) 42 International Tables for Crystallography, Volume A, Table 12. 1. 4. 2, p. 819 (2002)

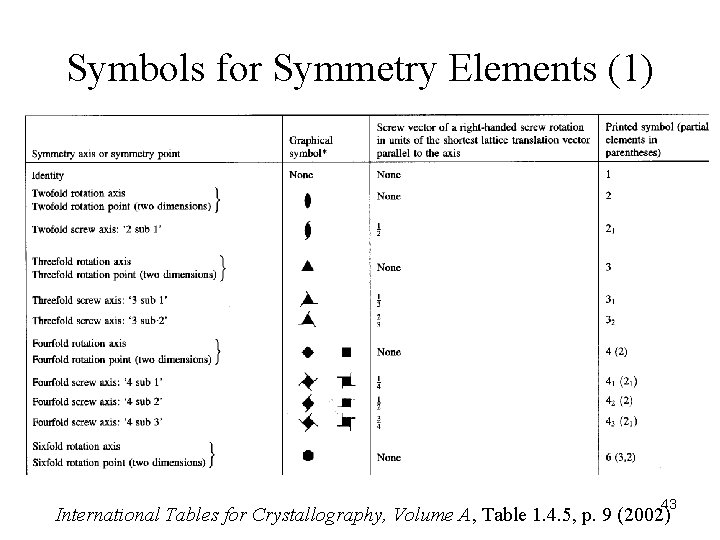
Symbols for Symmetry Elements (1) 43 International Tables for Crystallography, Volume A, Table 1. 4. 5, p. 9 (2002)

Symbols for Symmetry Elements (2) International Tables for Crystallography, Volume A, Table 1. 4. 5, p. 9 (2002)44

Symbols for Symmetry Elements (3) 45 International Tables for Crystallography, Volume A, Table 1. 4. 2, p. 7 (2002)

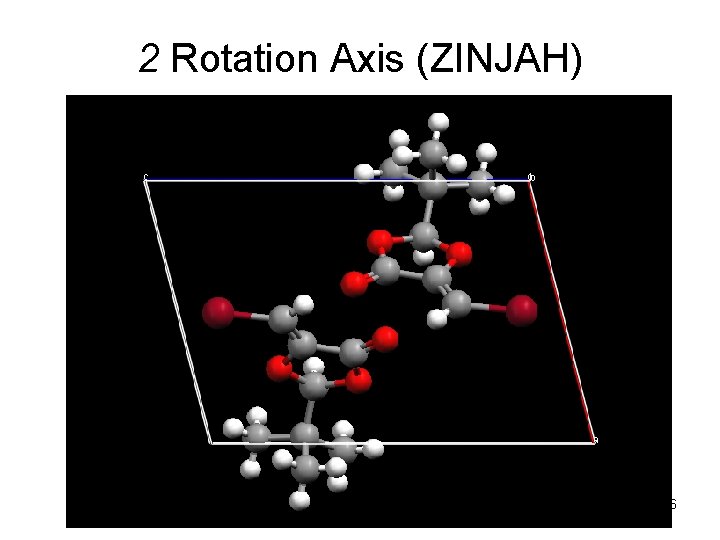
2 Rotation Axis (ZINJAH) 46

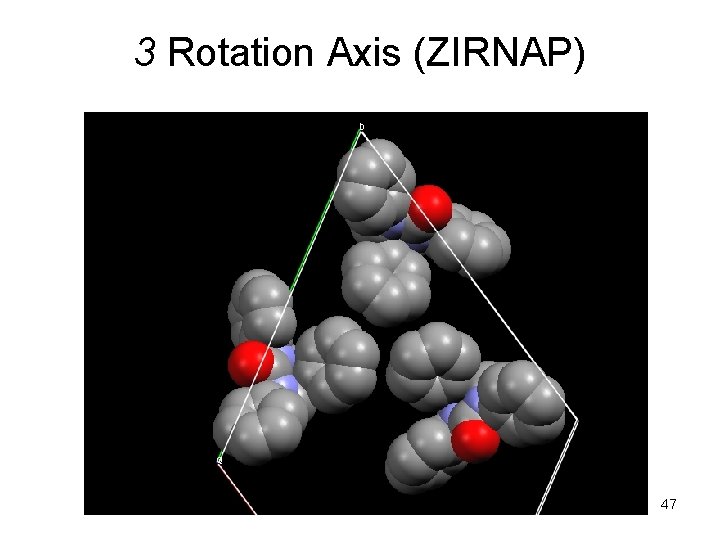
3 Rotation Axis (ZIRNAP) 47

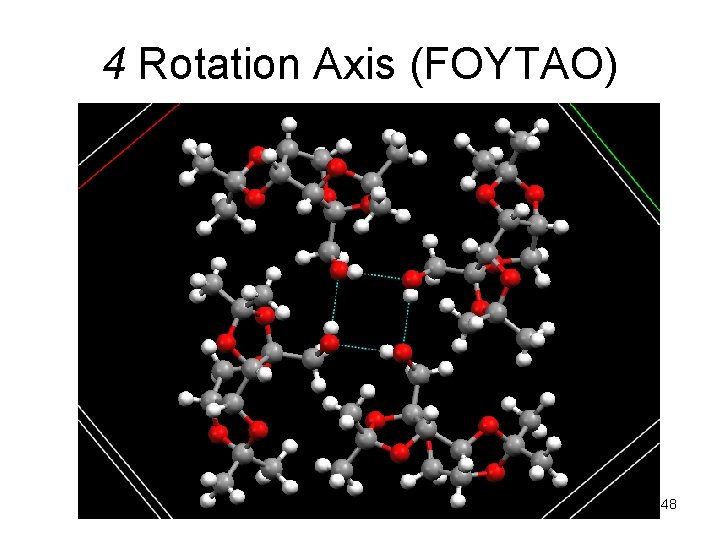
4 Rotation Axis (FOYTAO) 48

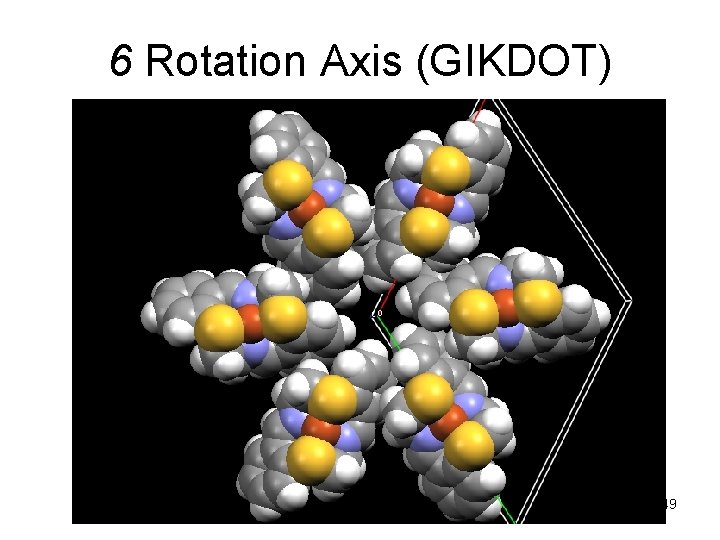
6 Rotation Axis (GIKDOT) 49

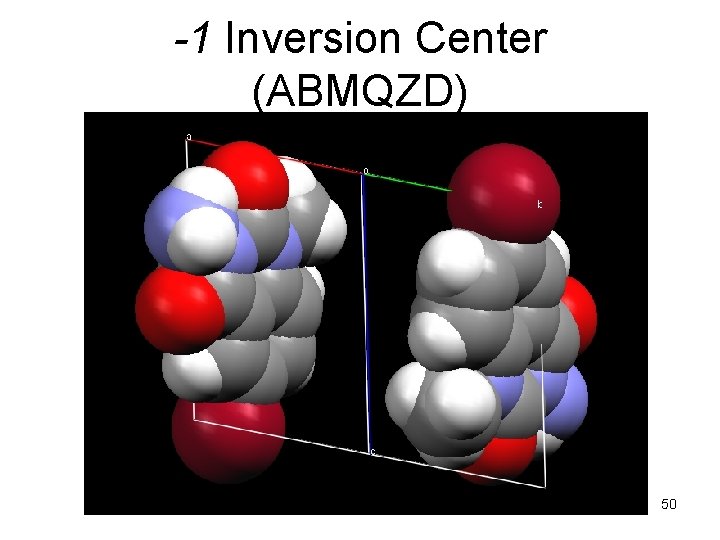
-1 Inversion Center (ABMQZD) 50

-2 Rotary Inversion Axis? 51

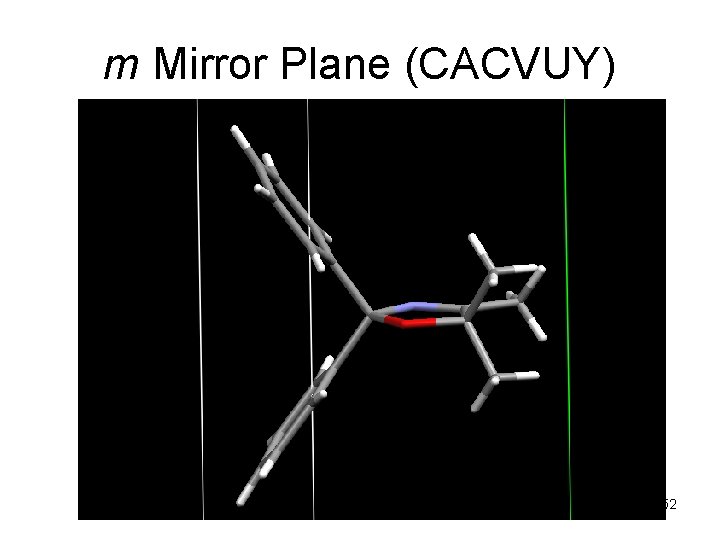
m Mirror Plane (CACVUY) 52

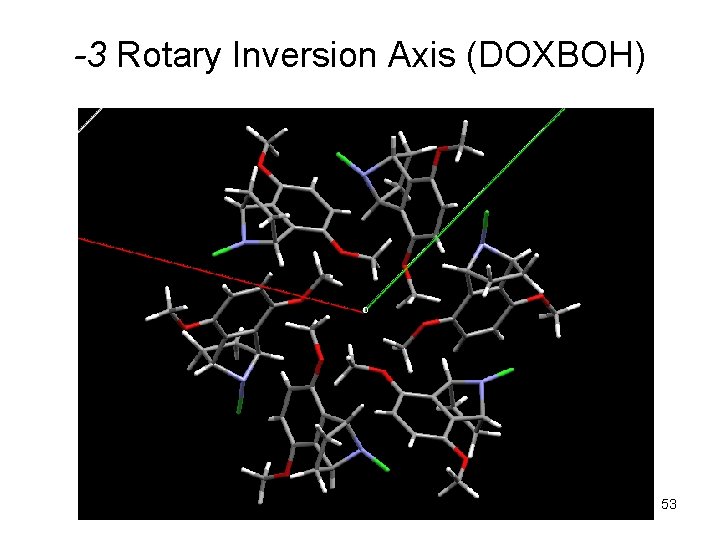
-3 Rotary Inversion Axis (DOXBOH) 53

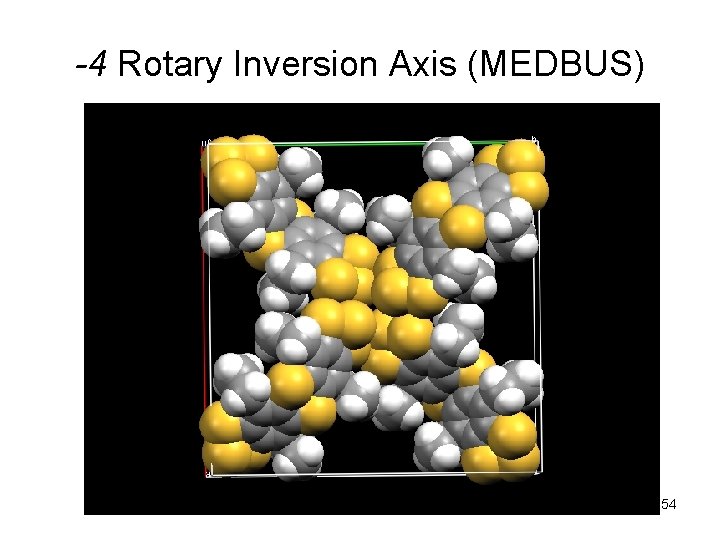
-4 Rotary Inversion Axis (MEDBUS) 54

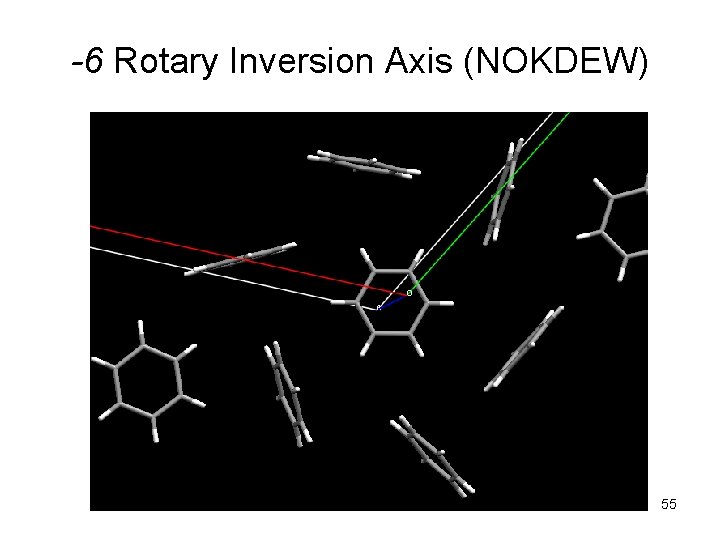
-6 Rotary Inversion Axis (NOKDEW) 55

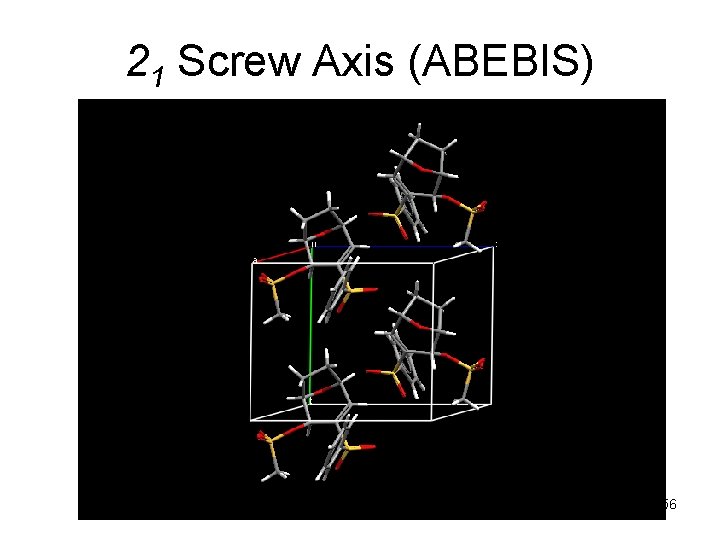
21 Screw Axis (ABEBIS) 56

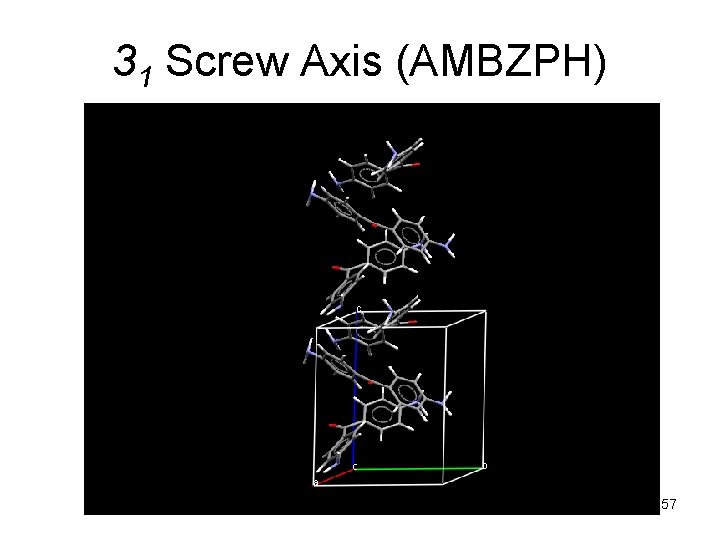
31 Screw Axis (AMBZPH) 57

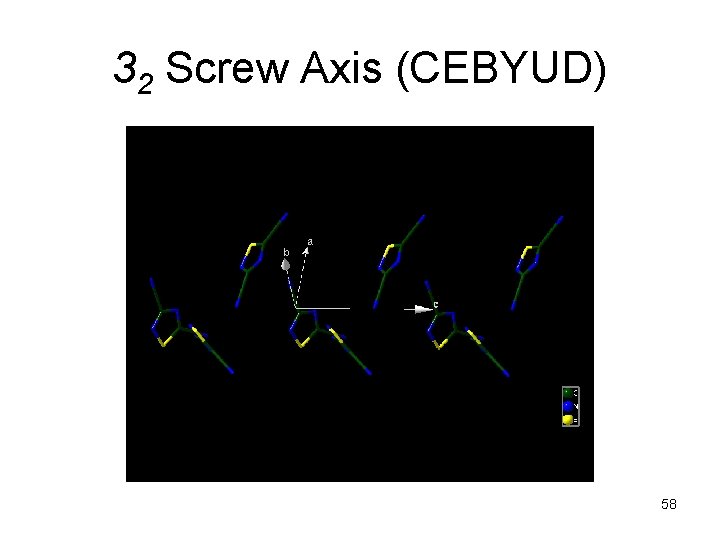
32 Screw Axis (CEBYUD) 58

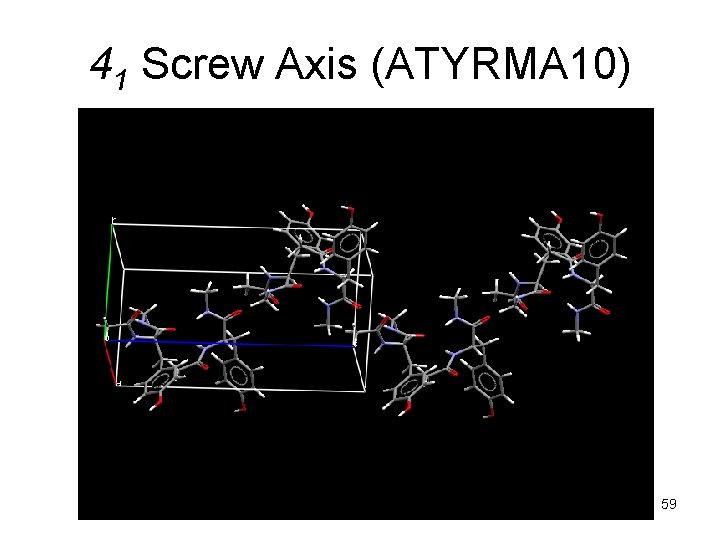
41 Screw Axis (ATYRMA 10) 59

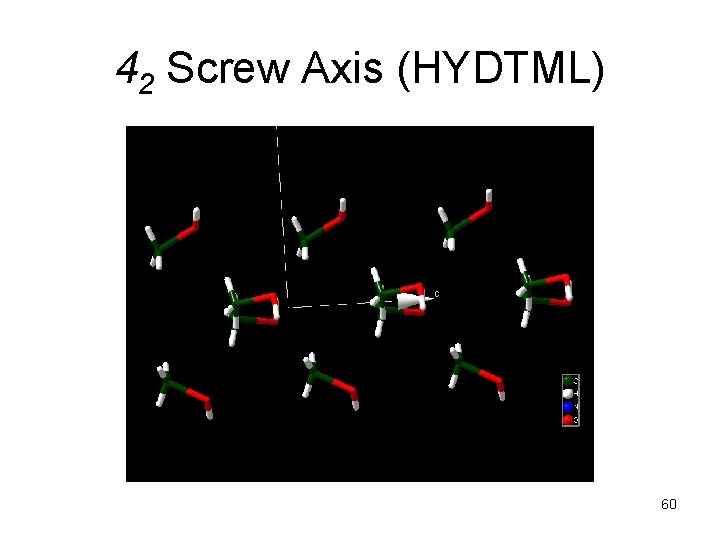
42 Screw Axis (HYDTML) 60

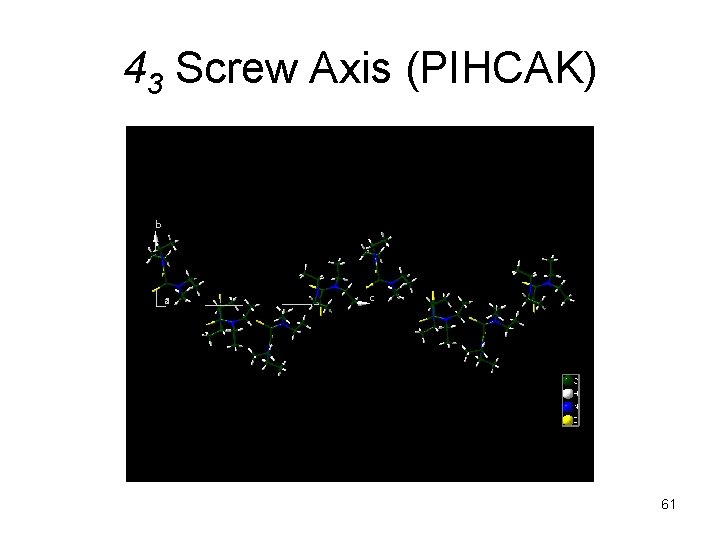
43 Screw Axis (PIHCAK) 61

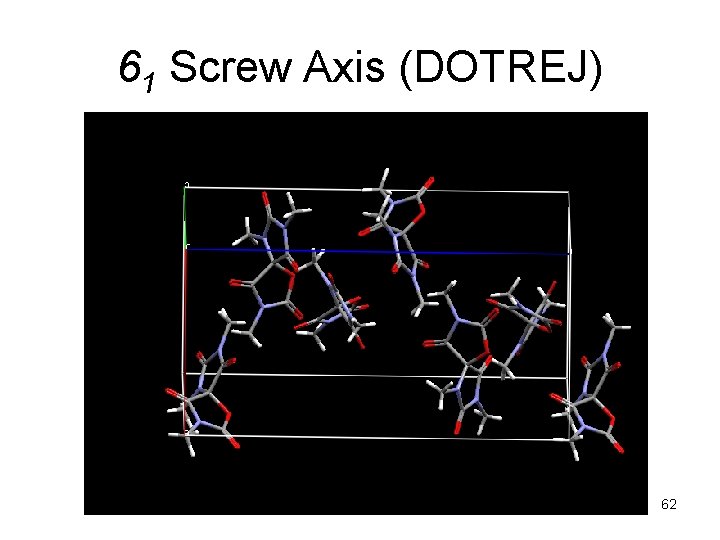
61 Screw Axis (DOTREJ) 62

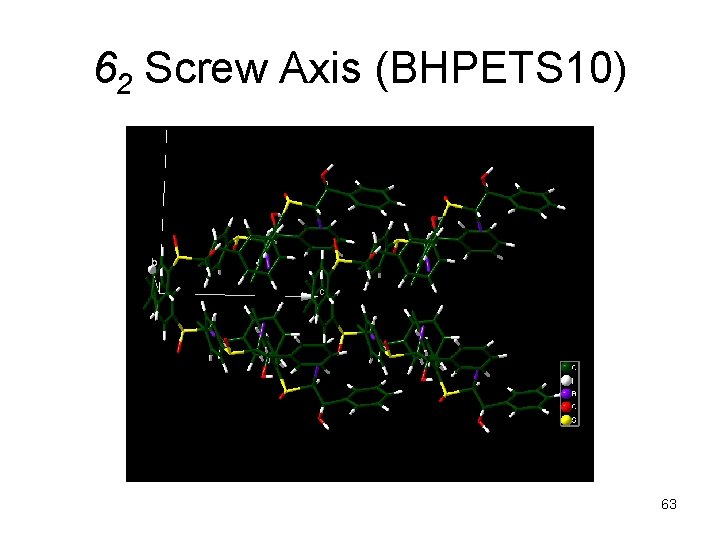
62 Screw Axis (BHPETS 10) 63

63 Screw Axis (NAIACE) 64

64 Screw Axis (TOXQUS) 65

65 Screw Axis (BEHPEJ) 66

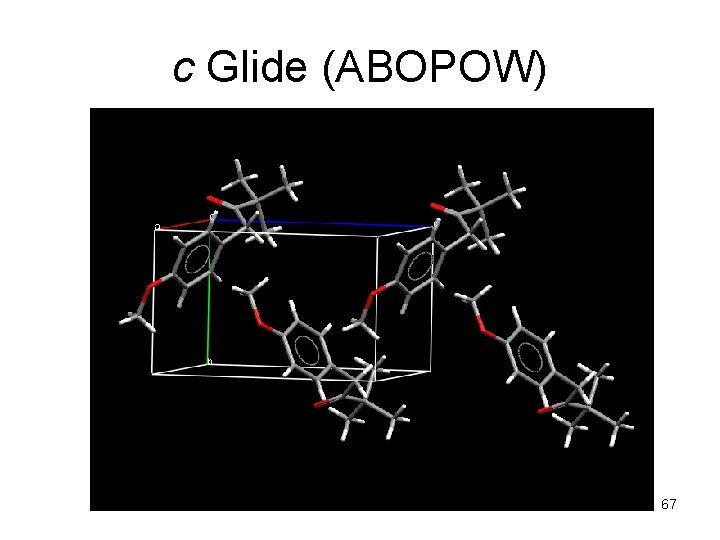
c Glide (ABOPOW) 67

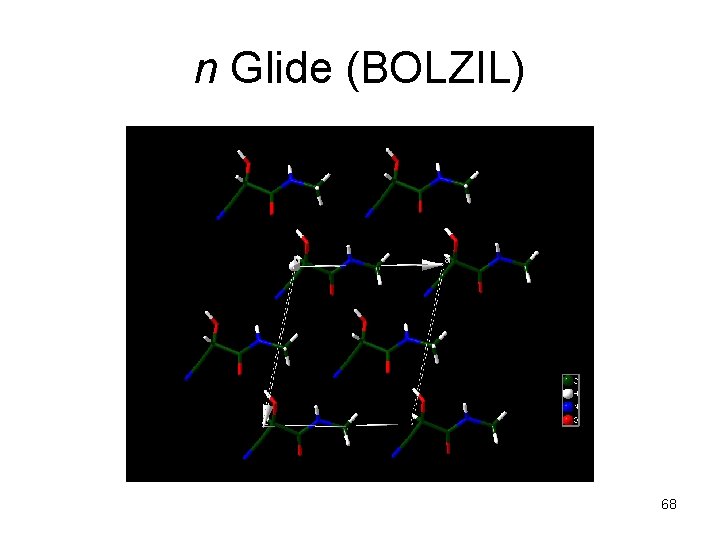
n Glide (BOLZIL) 68

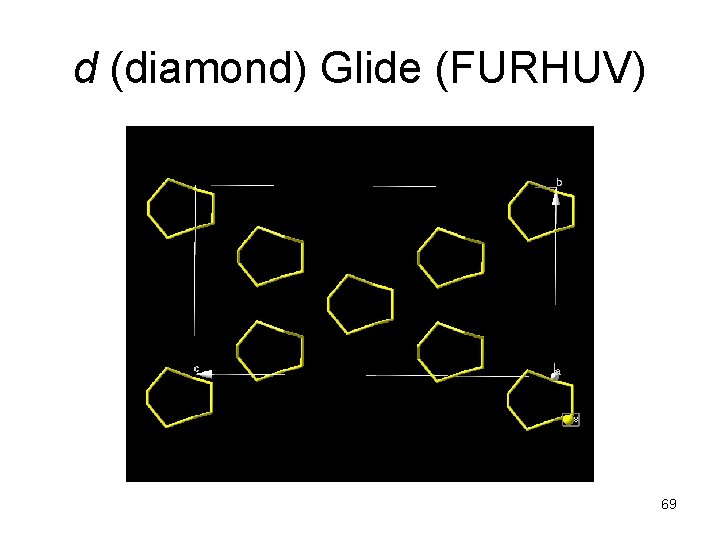
d (diamond) Glide (FURHUV) 69

What does all this mean? 70

Symmetry information is tabulated in International Tables for Crystallography, Volume A edited by Theo Hahn Fifth Edition 2002 71

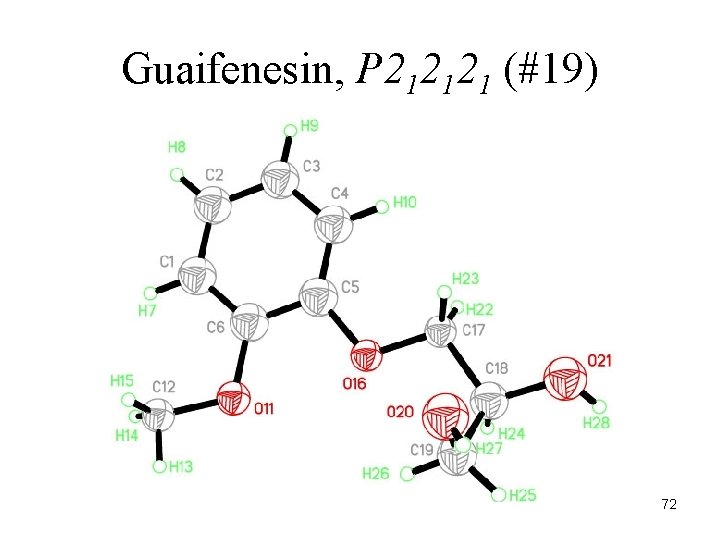
Guaifenesin, P 212121 (#19) 72

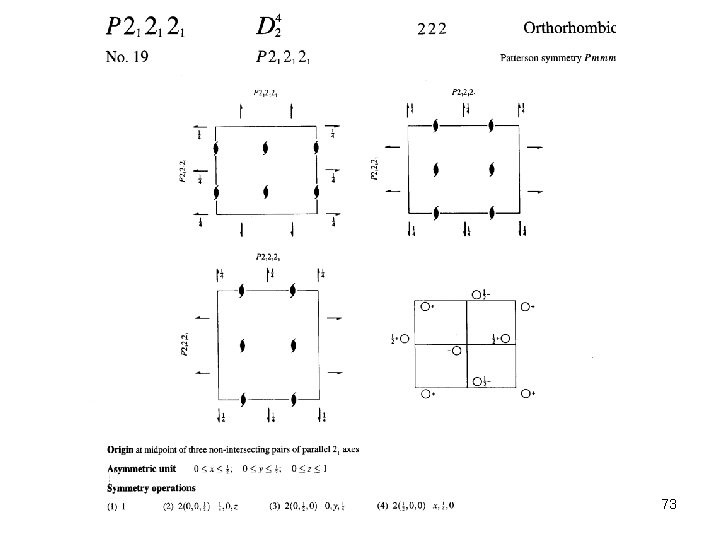
73

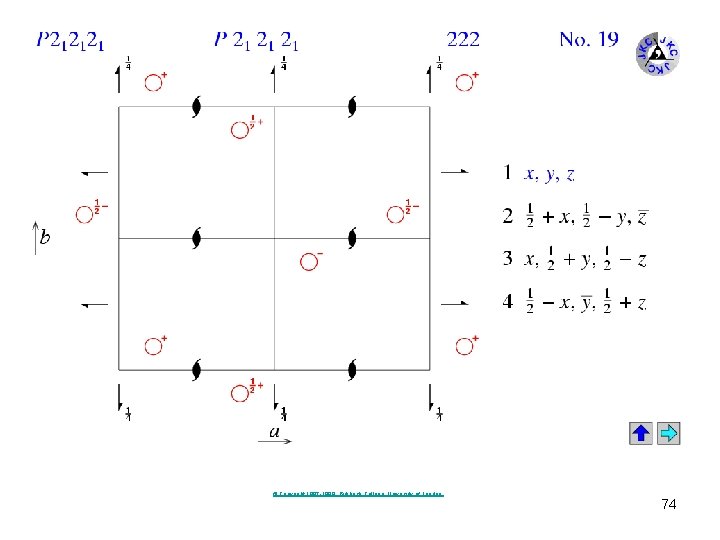
© Copyright 1997 -1999. Birkbeck College, University of London. 74

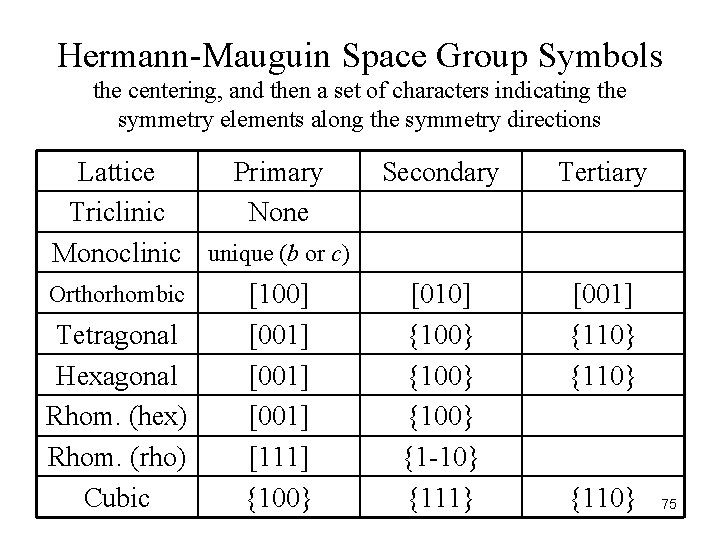
Hermann-Mauguin Space Group Symbols the centering, and then a set of characters indicating the symmetry elements along the symmetry directions Lattice Primary Triclinic None Monoclinic unique (b or c) Orthorhombic [100] Tetragonal [001] Hexagonal [001] Rhom. (hex) [001] Rhom. (rho) [111] Cubic {100} Secondary Tertiary [010] {100} {1 -10} {111} [001] {110} 75

Alternate Settings of Space Groups • • • Triclinic – none Monoclinic – (a) b or c unique, 3 cell choices Orthorhombic – 6 possibilities Tetragonal – C or F cells Trigonal/hexagonal – triple H cell Cubic • Different Origins 76

An Asymmetric Unit A simply-connected smallest closed volume which, by application of all symmetry operations, fills all space. It contains all the information necessary for a complete description of the crystal structure. 77

78

Sub- and Super-Groups • • Phase transitions (second-order) Overlooked symmetry Relations between crystal structures Subgroups – Translationengleiche (keep translations, lose class) – Klassengleiche (lose translations, keep class) – General (lose translations and class) 79

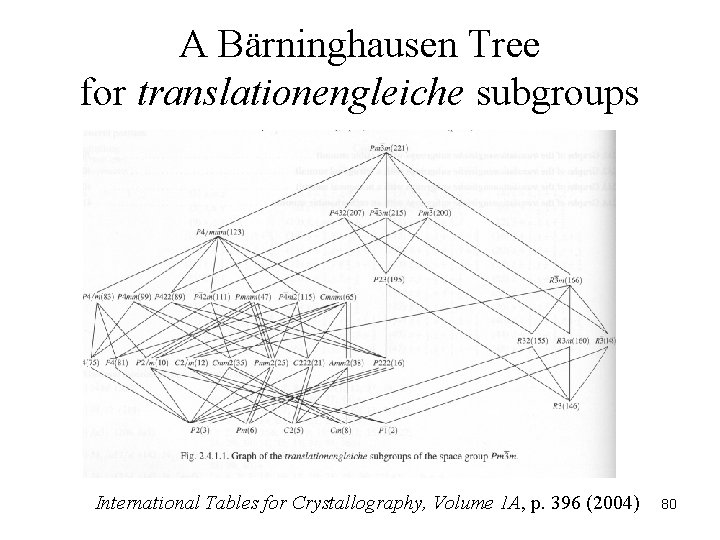
A Bärninghausen Tree for translationengleiche subgroups International Tables for Crystallography, Volume 1 A, p. 396 (2004) 80

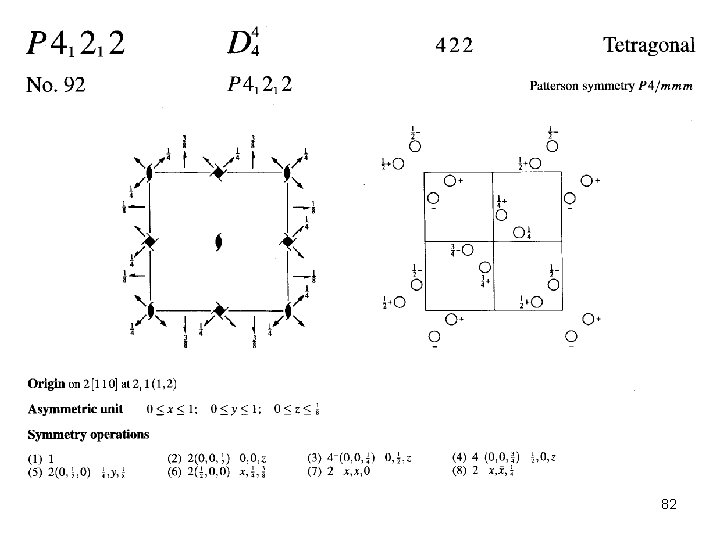
Mercury/ETGUAN (P 41212 #92) 81

82

83

Not all space groups are possible for protein crystals. 84

85

86

Some Classifications of Space Groups • Enantiomorphic, chiral, or dissymmetric – absence of improper rotations (including , = m, and ) • Polar – two directional senses are geometrically or physically different 87