New Lattice Based Cryptographic Constructions Oded Regev 1

New Lattice Based Cryptographic Constructions Oded Regev 1

Lattices • Basis: v 1, …, vn vectors in Rn • The lattice is a 1 v 1+…+anvn for all integer a 1, …, an. • What is the shortest vector u ? 2 v 1 v 1+v 2 v 1 2 v 2 -v 1 2 v 2 -2 v 1 0 2

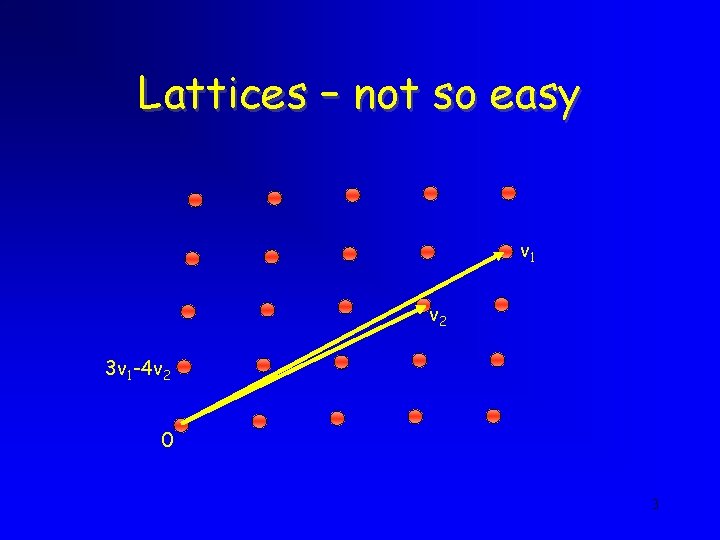
Lattices – not so easy v 1 v 2 3 v 1 -4 v 2 0 3

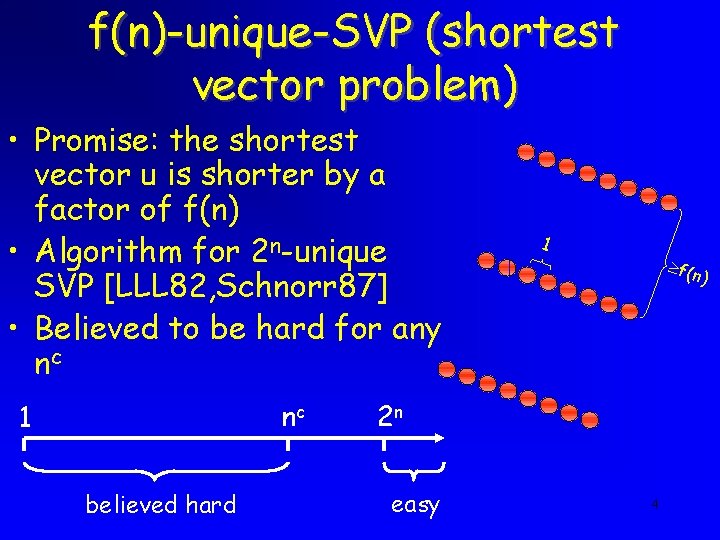
f(n)-unique-SVP (shortest vector problem) • Promise: the shortest vector u is shorter by a factor of f(n) • Algorithm for 2 n-unique SVP [LLL 82, Schnorr 87] • Believed to be hard for any nc nc 1 believed hard 1 f(n ) 2 n easy 4

History • Geometric objects with rich structure • Early work by Gauss 1801, Hermite 1850, Minkowski 1896 • More recent developments: – LLL Algorithm - approximates the shortest vector in a lattice [Lenstra. Lovàsz 82] • Factoring rational polynomials • Solving integer programs in a fixed dimension • Breaking knapsack cryptosystems – Ajtai’s average case connection [Ajtai 96] • Lattice based cryptosystems 5

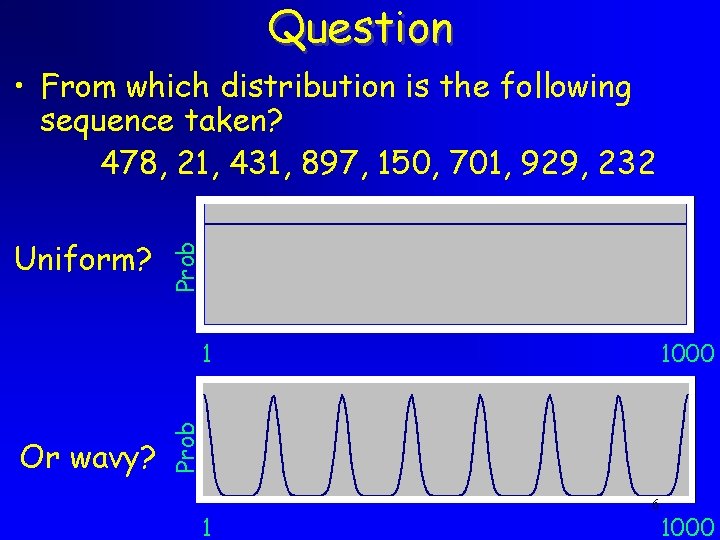
Question Uniform? Prob • From which distribution is the following sequence taken? 478, 21, 431, 897, 150, 701, 929, 232 Or wavy? 1000 Prob 1 1 6 1000

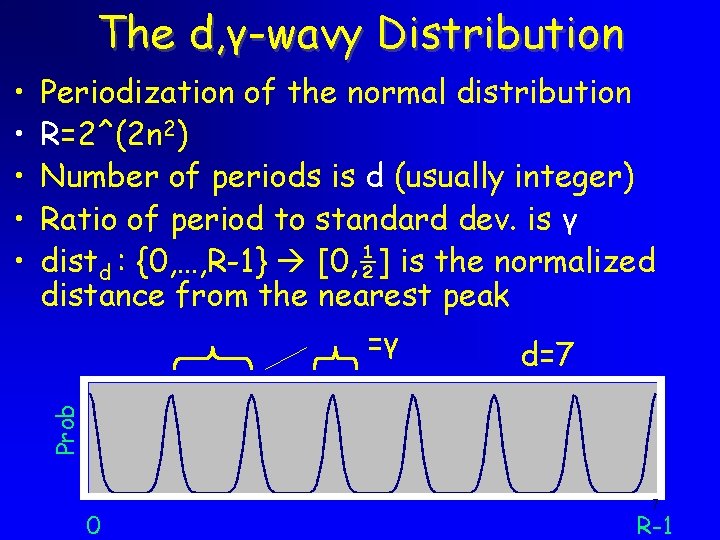
The d, γ-wavy Distribution Periodization of the normal distribution R=2^(2 n 2) Number of periods is d (usually integer) Ratio of period to standard dev. is γ distd : {0, …, R-1} [0, ½] is the normalized distance from the nearest peak =γ d=7 Prob • • • 0 7 R-1

Main Theorem • For all γ=γ(n), a reduction from γn 1/2 -unique Shortest Vector Problem to distinguishing between the uniform distribution and the d, γ-wavy distributions with an integer d<2^(n 2) 8

Average-case Theorem • For all γ=γ(n), a reduction from γn 1/2 -unique Shortest Vector Problem to distinguishing between the uniform distribution and the d, γ-wavy distributions for a non-negligible fraction of values d in [2^(n 2), 2 • 2^(n^2)] 9

Applications of Main Theorem 1. Public key encryption scheme 2. Collision resistant hash function 3. A problem in quantum computation 10

Cryptography • ‘Standard’ cryptography: • Usually based on factoring, discrete log, principal ideal problem • Average case assumption • Mostly broken by quantum computers • Lattice based cryptography [Ajtai 96, …]: • Based on lattice problems • Worst case assumption • Still not broken by quantum computers 11

Application 1 Public Key Encryption (PKE) • Consists of private key, public key, encryption and decryption • The Ajtai-Dwork cryptosystem [Ajtai. Dwork 96, Goldreich. Goldwasser. Halevi 97] • Previously, the only lattice based PKE with worst case assumption • Based on n 7 -unique Shortest Vector Problem 12

Application 1 Public Key Encryption (PKE) • We construct a new lattice based PKE from the average-case theorem: • Very simple description • Improves Ajtai-Dwork to n 1. 5 -unique Shortest Vector Problem • Uses integer numbers, very efficient 13

Application 2 Collision Resistant Hash Function • A function f: {0, 1}r {0, 1}s with r>s such that it is hard to find collisions, i. e. , x y s. t. f(x)=f(y) • Many previous constructions [Ajtai 96, Goldreich. Goldwasser. Halevi 96, Cai. Nerurkar 97, Cai 99, Micciancio 02] • Our construction is • The first which is not based on Ajtai’s iterative step 14 • Somewhat stronger (based on n 1. 5 -u. SVP)

Application 3 Quantum Computation • Quantum computers can break cryptography based on factoring [Shor 96] • Based on the HSP on Abelian groups • What about lattice based cryptography? 15

Application 3 Quantum Computation • Lattice based cryptography can be broken using the HSP on Dihedral groups [R’ 02] • Our main theorem explains the failure of previous attempts to solve the HSP on Dihedral groups [Ettinger. Hoyer’ 00] 16

Main Theorem • For all γ=γ(n), a reduction from γn 1/2 -unique Shortest Vector Problem to distinguishing between the uniform distribution and the d, γ-wavy distributions with an integer d<2^(n 2) 17

Proof of the Main Theorem 18

Proof Outline n 1. 5 -Unique-SVP decision problem promise problem n-dim distributions Main theorem 19

Reduction to: Decision Problem • Given a n 1. 5 -unique lattice, and a prime p>n 1. 5 • Assume the shortest vector is: u = a 1 v 1+a 2 v 2+…+anvn • Decide whether a 1 is divisible by p 20

The Reduction • Idea: decrease the coefficients of the shortest vector • If we find out that p|a 1 then we can replace the basis with pv 1, v 2, …, vn. • u is still in the new lattice: u = (a 1/p) • pv 1 + a 2 v 2 + … + anvn • The same can be done whenever p|ai for some i 21

The Reduction • But what if p | ai for all i ? • Consider the basis v 1, v 2 -v 1, v 3, …, vn • The shortest vector is u = (a 1+a 2)v 1 + a 2(v 2 -v 1) + a 3 v 3 + … + anvn • The first coefficient is a 1+a 2 • Similarly, we can set it to a 1 -bp/2 ca 2 , …, a 1 -a 2 , a 1+a 2 , … , a 1+bp/2 ca 2 • One of them is divisible by p, so we choose it and continue 22

Proof Outline n 1. 5 -Unique-SVP decision problem promise problem n-dim distributions Main theorem 23

Reduction from: Decision Problem • Given a n 1. 5 -unique lattice, and a prime p>n 1. 5 • Assume the shortest vector is: u = a 1 v 1+a 2 v 2+…+anvn • Decide whether a 1 is divisible by p 24

Reduction to: Promise Problem • Given a lattice, distinguish between: Case 1. Shortest vector is of length 1/n and all non -parallel vectors are of length more than n Case 2. Shortest vector is of length more than n 25

The reduction • Input: a basis (v 1, …, vn) of a n 1. 5 unique lattice • Scale the lattice so that the shortest vector is of length 1/n • Replace v 1 by pv 1. Let M be the resulting lattice • If p | a 1 then M has shortest vector 1/n and all non-parallel vectors more than n • If p | a 1 then M has shortest vector more than n 26

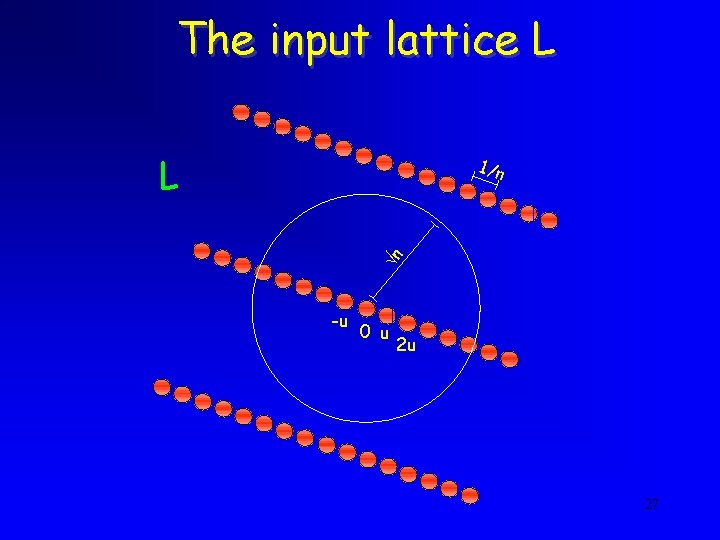
The input lattice L L n 1/n -u 0 u 2 u 27

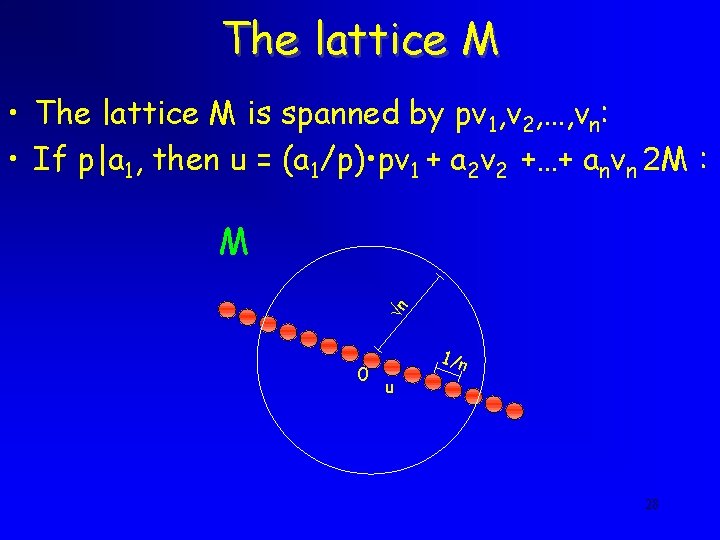
The lattice M • The lattice M is spanned by pv 1, v 2, …, vn: • If p|a 1, then u = (a 1/p) • pv 1 + a 2 v 2 +…+ anvn 2 M : n M 0 u 1/n 28

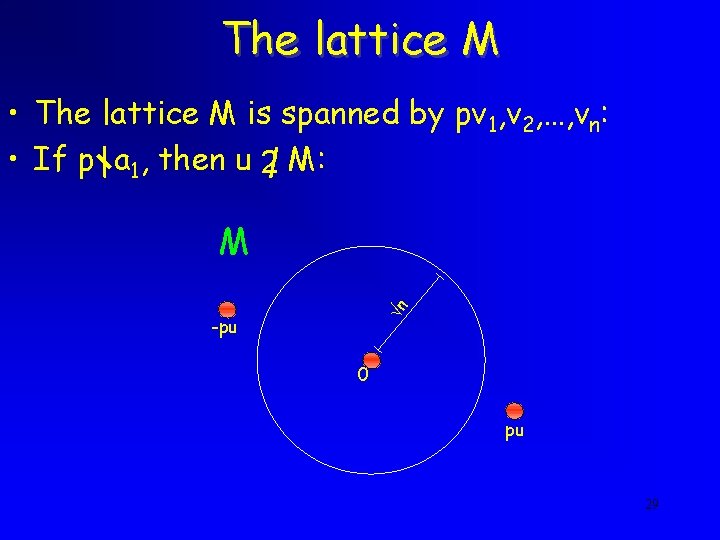
The lattice M • The lattice M is spanned by pv 1, v 2, …, vn: • If p | a 1, then u 2 M: n M -pu 0 pu 29

Proof Outline n 1. 5 -Unique-SVP decision problem promise problem n-dim distributions Main theorem 30

Reduction from: Promise Problem • Given a lattice, distinguish between: Case 1. Shortest vector is of length 1/n and all non -parallel vectors are of length more than n Case 2. Shortest vector is of length more than n 31

n-dimensional distributions • Distinguish between the distributions: ? Wavy Uniform 32

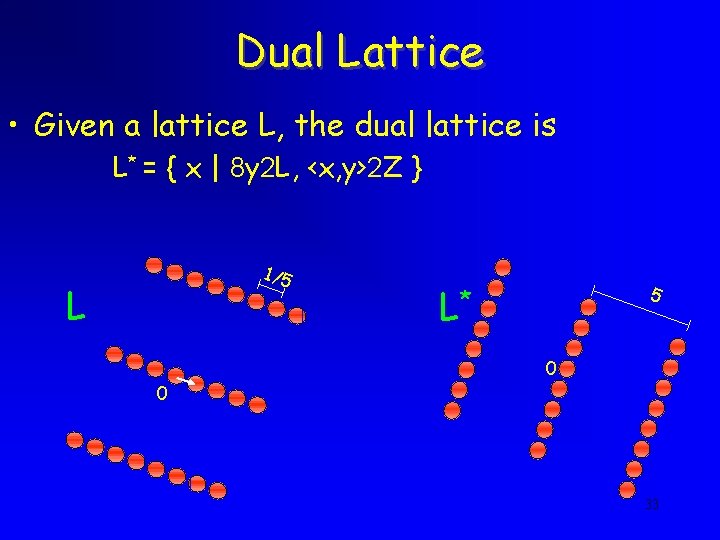
Dual Lattice • Given a lattice L, the dual lattice is L* = { x | 8 y 2 L, <x, y>2 Z } 1/5 L L* 5 0 0 33

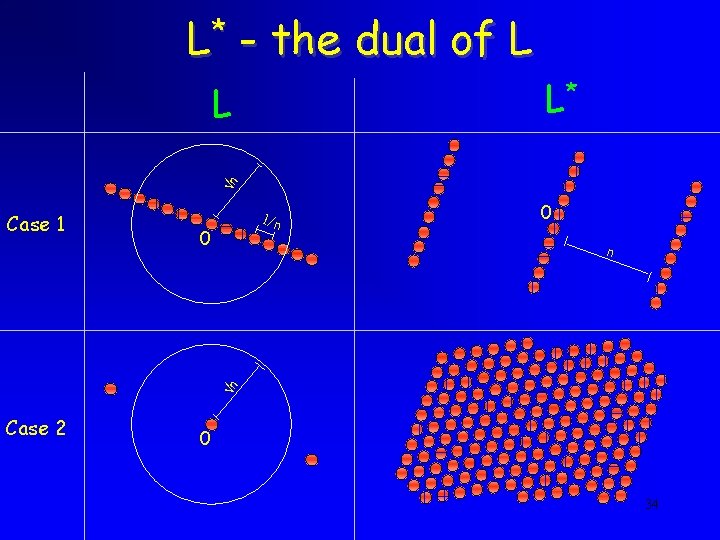
L* - the dual of L L* n L 1/n 0 0 n n Case 1 Case 2 0 34

Reduction • Choose a point randomly from L* • Perturb it by a Gaussian of radius n 35

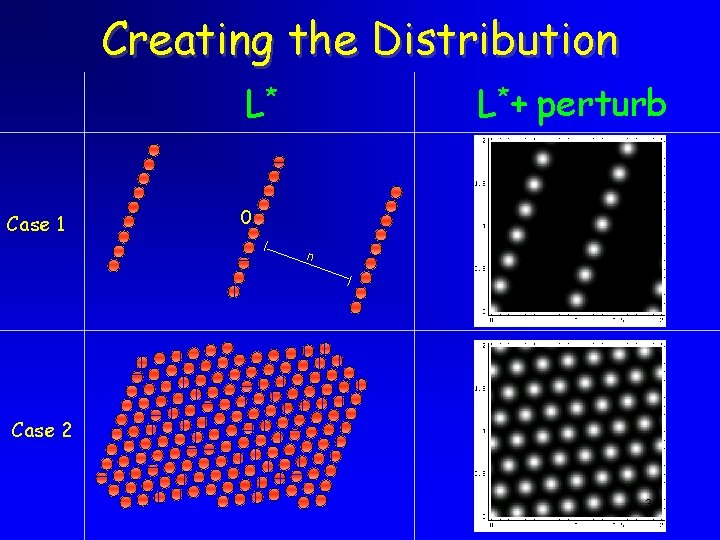
Creating the Distribution L* Case 1 L*+ perturb 0 n Case 2 36

Analyzing the Distribution • Theorem: (using [Banaszczyk’ 93]) The distribution obtained above depends only on the points in L of distance n from the origin (up to an exponentially small error) • Therefore, Case 1: Determined by multiples of u wavy on hyperplanes orthogonal to u Case 2: Determined by the origin uniform 37

Proof of Theorem • For a set A in Rn, define: • Poisson Summation Formula implies: • Banaszczyk’s theorem: For any lattice L, 38

Proof of Theorem (cont. ) • In Case 2, the distribution obtained is very close to uniform: • Because: 39

Proof Outline n 1. 5 -Unique-SVP decision problem promise problem n-dim distributions Main theorem 40

n-dimensional distributions • Distinguish between the distributions • Given by an oracle that returns points inside a cube of side length 2 n ? Wavy Uniform 41

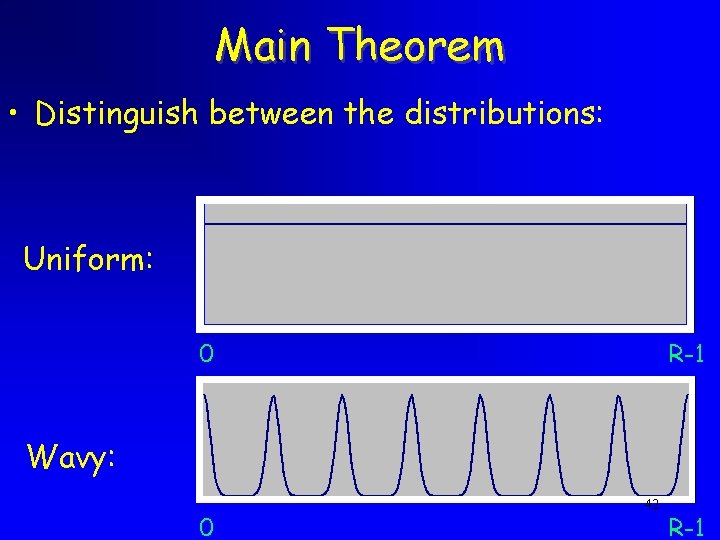
Main Theorem • Distinguish between the distributions: Uniform: 0 R-1 Wavy: 0 42 R-1

Reducing to 1 -dimension • First attempt: sample and project to a line 43

Reducing to 1 -dimension • But then we lose the wavy structure! • We should project only from points very close to the line 44

The solution • Use the periodicity of the distribution • Project on a ‘dense line’ : 45

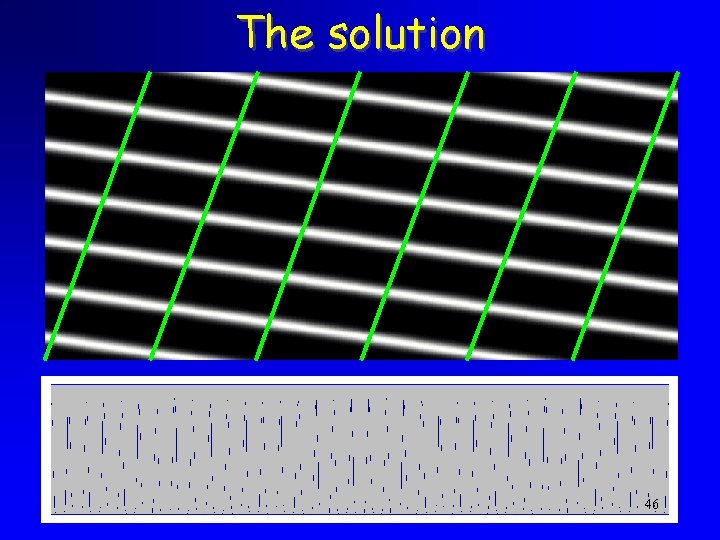
The solution 46

The solution • We choose the line that connects the origin to e 1+Ke 2+K 2 e 3…+Kn-1 en where K is large enough • • The distance between hyperplanes is n The sides are of length 2 n Therefore, we choose K=2 O(n) Hence, d<O(Kn)=2^(O(n 2)) 47

Done n 1. 5 -Unique-SVP decision problem promise problem n-dim distributions Main theorem 48

From Worst-Case to Average-Case 49

Worst-case vs. Average-case • Main theorem presents a problem that is hard in the worst-case: distinguish between uniform and d, γ-wavy distributions for all integers d<2^(n 2) • For cryptographic applications, we would like to have a problem that is hard on the average: distinguish between uniform and d, γ -wavy distributions for a non-negligible fraction of d in [2^(n 2), 2 • 2^(n 2)] 50

Compressing • The following procedure transforms d, γ-wavy into 2 d, γ-wavy for all integer d: – Sample a from the distribution – Return either a/2 or (a+R)/2 with probability ½ • In general, for any real a 1, we can compress d, γ-wavy into ad, γ-wavy • Notice that compressing preserves the uniform distribution • We show a reduction from worst-case to 51 average-case

Reduction • Assume there exists a distinguisher between uniform and d, γ-wavy distribution for some nonnegligible fraction of d in [2^(n 2), 2 • 2^(n 2)] • Given either a uniform or a d, γ-wavy distribution for some integer d<2^(n 2) repeat the following: – Choose a in {1, …, 2¢ 2^(n 2)} according to a certain distribution – Compress the distribution by a – Check the distinguisher’s acceptance probability • If for some a the acceptance probability differs from that of uniform sequences, return ‘wavy’; otherwise, return ‘uniform’ 52

Reduction • Distribution is uniform: – After compression it is still uniform – Hence, the distinguisher’s acceptance probability equals that of uniform sequences for all a • Distribution is d, γ-wavy: – After compression it is in the good range with some probability – Hence, for some a, the distinguisher’s acceptance probability differs from that of uniform sequences 1 … d 2^(n 2) … 2¢ 2^(n 2) 53

Application 1 Public Key Encryption Scheme 54

PKE – Description • Let m=2 log 2 R=4 n 2 • Private key: – A real number y chosen uniformly in [2^(n 2), 2¢ 2^(n 2)] such that y is close to an integer ( 1/100 m) • Public key: – Choose integers A={a 1, …, am} from the y, γ-wavy distribution with γ=n 1+ε • Lemma: Public keys are indistinguishable from uniform sequences (based on n 1. 5+ε unique-SVP) 55

PKE – Description (cont. ) • Private key: y • Public key: A={a 1, …, am} • Encryption: – Bit 0: a number chosen uniformly in {0, …, R-1} – Bit 1: the sum of a random subset of A mod R • Decryption of w: – If disty(w)<1/50 then 1 otherwise 0 56

PKE – Correctness • Encryption of the bit 0: – With probability 96%, disty( Sai)>1/50 – These errors can be avoided • Encryption of the bit 1: – For a subset S, with high probability, disty( Sai)<1/100 – Using Sai < m¢R, disty( Sai mod R)<1/50 57

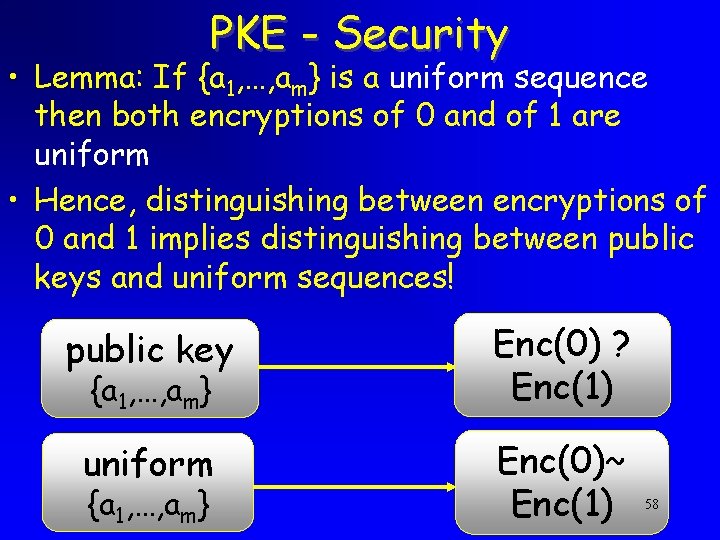
PKE - Security • Lemma: If {a 1, …, am} is a uniform sequence then both encryptions of 0 and of 1 are uniform • Hence, distinguishing between encryptions of 0 and 1 implies distinguishing between public keys and uniform sequences! public key Enc(0) ? Enc(1) uniform Enc(0)~ Enc(1) {a 1, …, am} 58

PKE – Security • Lemma: Public keys are indistinguishable from uniform sequences (based on n 1. 5+ε unique-SVP) • Proof: Follows from the average-case theorem (since we choose y from a set of size 1/(50 m) of all [2^(n 2), 2¢ 2^(n 2)]) 59

Application 2 Collision Resistant Hash Function 60

Collision Resistant Hash Function • Choose a 1, …, am uniformly in {0, …, R-1} where m=2 log 2 R=4 n 2. Then: b 1, …, bm {0, 1}, f(b 1, …, bm)=Σbiai mod R • We will see a simpler proof based on n 2. 5+εu. SVP 61

Collision Resistant Hash Function • Assume there exists a collision finding algorithm C • I. e. , with non-negligible probability, given a 1, …, am chosen uniformly, C finds c 1, …, cm {-1, 0, 1} (not all zero) such that Σaici = 0 (mod R) 62

Collision Resistant Hash Function • We show to distinguish between the uniform and the d, γ-wavy with γ=n 2+ε using C • Choose z uniformly from {0, …, R-1} • With probability 0. 9, distd(z) > 1/20 • Repeat the following enough times: • Choose a 1, …, am from the unknown distribution • Call C with a 1, …, ak-1, (ak+z mod R), ak+1, …, am where k is chosen uniformly from {1, …, m} • If ck is always zero or C keeps failing, say ‘wavy’ otherwise ‘uniform’ 63

Correctness • Distribution is uniform: • a 1, …, ak-1, (ak+z mod R), ak+1, …, am has the same distribution as a uniform sequence • Therefore, C answers with non-negligible probability and ck 0 with probability at least 1/m • Distribution is d, γ-wavy: • W. h. p. , i {1, …, m}, distd(ai) < 1/(100 n 2) • For all c 1, …, cm {-1, 0, 1}, distd(Σciai) < 1/25 (since m=4 n 2) • Therefore, if z has distd(z) > 1/20 then it can never be included in the sum, i. e. , ck=0 64

Application 3 Quantum Computation – The Dihedral HSP 65

Hidden Subgroup Problem • Given a function that is constant and distinct on cosets of H G, find H • Solved for Abelian groups • Also for certain non-Abelian groups [Rötteler. Beth’ 98, Hallgren. Russell. Tashma’ 00, Grigni. Schulman Vazirani’ 01…] • Still open for many groups. In particular: – Symmetric group – Dihedral group (ZN Z 2) 66

Solving Dihedral HSP • Two approaches: • Ettinger and Høyer ’ 00 – Reduction to “Period finding from samples” • R ’ 02, Kuperberg ‘ 03 – Reduction to average case subset sum 67

Solving Dihedral HSP • Idea of Ettinger and Høyer: – Reduce to “Hidden Translation on ZN”: Given an oracle that outputs states of the form |xi+|x+di where x is arbitrary and d is fixed, find d – Take the Fourier transform – Measure 68

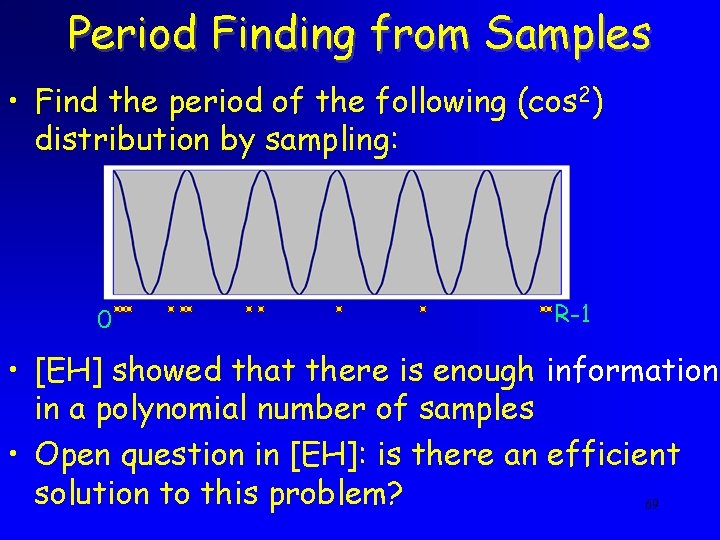
Period Finding from Samples • Find the period of the following (cos 2) distribution by sampling: 0 R-1 • [EH] showed that there is enough information in a polynomial number of samples • Open question in [EH]: is there an efficient solution to this problem? 69

Reduction • Lemma: A distinguisher between cos 2 and the uniform distribution implies a distinguisher between the wavy and uniform distribution 70

Guess the period and add noise 71

Reduction • Corollary: finding the period of the cos 2 distribution is hard • Proof: Since all cos 2 distributions look like uniform, they all look the same 72

Conclusion • Main theorem • Average case form • Applications – Strong public key encryption scheme – Collision resistant hash function – Solution to an open question in quantum computation • Other applications? 73