Inelastic scattering When the scattering is not elastic

Inelastic scattering When the scattering is not elastic (new particles are produced) the energy and direction of the scattered electron are independent variables, unlike the elastic scattering situation. W is the mass squared of the produced hadronic system From the measurement of the direction (solid angle element d ) and the energy E' of the scattered electron, the four momentum transfer Q 2=-q 2 can be calculated. The differential cross-section is determined as a function of E' and Q 2. 2004, Torino Aram Kotzinian e(k', E') e (k, E) (q) N (P, M) W 1

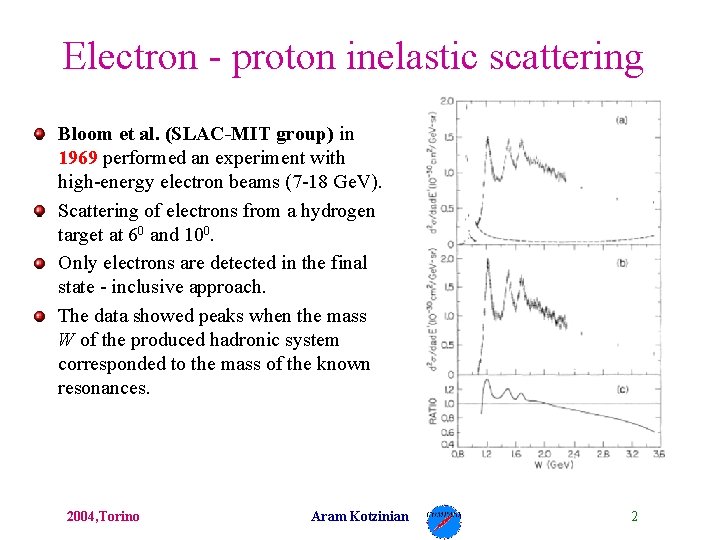
Electron - proton inelastic scattering Bloom et al. (SLAC-MIT group) in 1969 performed an experiment with high-energy electron beams (7 -18 Ge. V). Scattering of electrons from a hydrogen target at 60 and 100. Only electrons are detected in the final state - inclusive approach. The data showed peaks when the mass W of the produced hadronic system corresponded to the mass of the known resonances. 2004, Torino Aram Kotzinian 2

Inelastic scattering cross-section Similar to the electron-proton elastic scattering, the differential cross-section of electron-proton inelastic scattering can be written in a general form: The cross-section is double differential because and E ' are independent variables. The expression contains Mott cross-section as a factor and is analogous to the Rosenbluth formula. It isolates the unknown shape of the nucleon target in two structure functions W 1 and W 2, which are the functions of two independent variables and q 2. The structure functions correspond to the two possible polarisation states of the virtual photon: longitudinal and transverse. Longitudinal polarisation exists only because photon is virtual and has a mass. For elastic scattering, (P+q)2=M 2 and the two variables and Q 2 are related by Q 2=2 M . 2004, Torino Aram Kotzinian 3

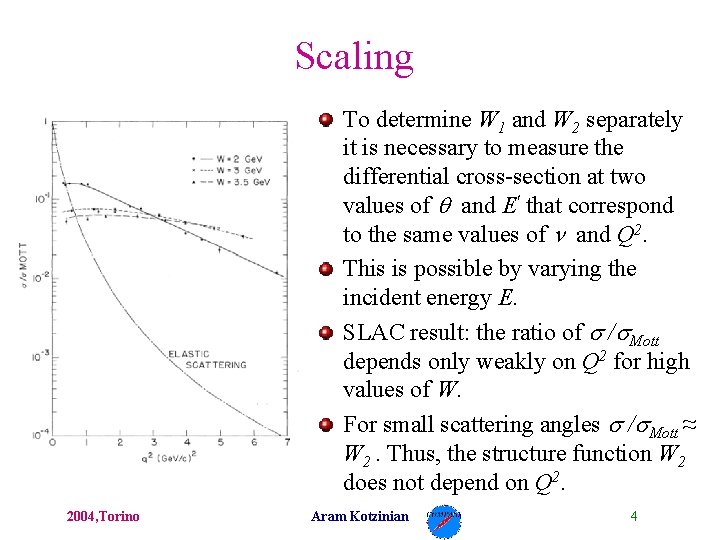
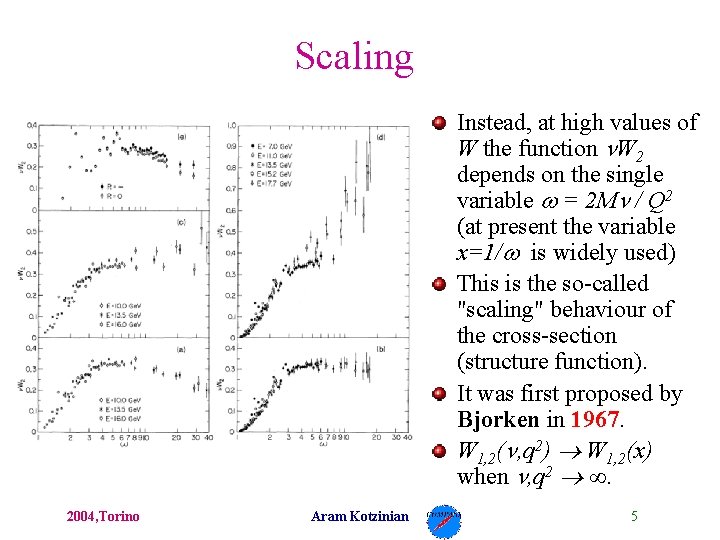
Scaling To determine W 1 and W 2 separately it is necessary to measure the differential cross-section at two values of and E' that correspond to the same values of and Q 2. This is possible by varying the incident energy E. SLAC result: the ratio of / Mott depends only weakly on Q 2 for high values of W. For small scattering angles / Mott ≈ W 2. Thus, the structure function W 2 does not depend on Q 2. 2004, Torino Aram Kotzinian 4

Scaling Instead, at high values of W the function W 2 depends on the single variable = 2 M / Q 2 (at present the variable x=1/ is widely used) This is the so-called "scaling" behaviour of the cross-section (structure function). It was first proposed by Bjorken in 1967. W 1, 2( , q 2) W 1, 2(x) when , q 2 ∞. 2004, Torino Aram Kotzinian 5

Deep Inelastic Scattering (DIS) z-axis to be along the incident lepton beam direction. 2004, Torino Kinematic Variables M --The mass of the target hadron. E -- The energy of the incident lepton. k -- The momentum of the initial lepton. W -- The solid angle into which the outgoing lepton is scattered. E’ -- The energy of the scattered lepton. K’ -- The momentum of the scattered lepton, K’ = (E’; E’sinqcosf; E’sinqsinf; E’cos ). P -- The momentum of the target, p = (M; 0; 0; 0), for a fixed target experiment. q = k-k’ -- the momentum transfer in the scattering process, i. e. the momentum of the virtual photon. Aram Kotzinian 6

Important variables The invariant mass of the final hadronic system X is 2004, Torino Aram Kotzinian 7

Some inequalities The invariant mass of X must be at least that of a nucleon, since baryon number is conserved in the scattering process. Since Q 2 and n are both positive, x must also be positive. The lepton energy loss E-E’ must be between zero and E, so the physically allowed kinematic region is The value x = 1 corresponds to elastic scattering. 2004, Torino Aram Kotzinian 8

Any fixed hadron state X with invariant mass cross-section at the value of x contributes to the In the DIS limit So, any hadron state X with fixed invariant mass gets driven to x=1 The experimental measurements give the cross-section as a function of the final lepton energy and scattering angle. The results are often presented instead by giving the differential cross-section as a function of (x, ) or (x, y). The Jacobian for converting between these cases is easily worked out using the definitions of the kinematic variables 2004, Torino Aram Kotzinian 9

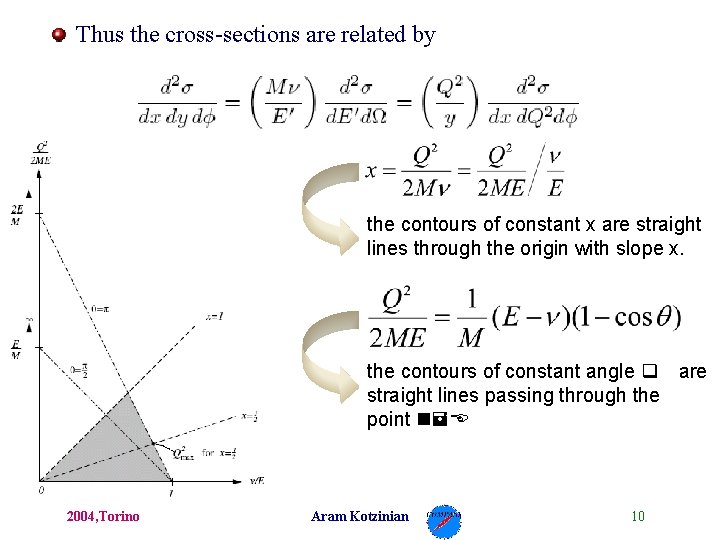
Thus the cross-sections are related by the contours of constant x are straight lines through the origin with slope x. the contours of constant angle q are straight lines passing through the point n=E 2004, Torino Aram Kotzinian 10

For fixed value of x, the maximum allowed value of It is useful to have formulae for the different components of q as a function of x and y. This expressions are valid in the Lab frame with z-axis along lepton momentum 2004, Torino Aram Kotzinian 11

Expression for DIS cross section The scattering amplitude M is given by 2004, Torino Aram Kotzinian 12

It is conventional to define the leptonic tensor The definition of the hadronic tensor is slightly more complicated. Inserting a complete set of states gives where the sum on X is a sum over the allowed phase space for the final state X 2004, Torino Aram Kotzinian 13

Translation invariance implies that Only the first term contributes, since and Using leptonic and hadronic tensors we have 2004, Torino Aram Kotzinian 14

Finally, integrating over azimuth, we get 2004, Torino Aram Kotzinian 15

Leptonic tensor The polarization of a spin 1/2 particle can be described by a spin vector defined in the rest frame of the particle by The spin vector in arbitrary frame is obtained by Lorentz boost 2004, Torino Aram Kotzinian 16

For a spin-1/2 particle at rest with spin along the z-axis, the spin vector is. This differs from the conventional normalization of s by a factor of the fermion mass m. Here we use the relativistic spinors normalized to 2 E. In the extreme relativistic limit have s=Hk, where k is the lepton momentum and H is the lepton helicity. Using trace theorems we obtain for leptonic tensor Unpolarized lepton beam probes only the symmetric part of hadronic tensor 2004, Torino Aram Kotzinian 17

The Hadronic Tensor for Spin-1/2 Targets Using parity, time-reversal invariance, hermiticity and current conservation one can show that Where the structure functions Often another structure functions are used in the literature: 2004, Torino Aram Kotzinian 18

Scaling The hadronic tensor is dimensionless The structure functions are dimensionless functions of the Lorentz invariant variables It is conventional to write them as functions of They can be written as dimensionless functions of the dimensionless variables In elastic scattering there is a strong dependence on , and the elastic form factors fall o like a power of. Bjorken: in DIS the structure functions only depend on x, and must be independent of 2004, Torino Aram Kotzinian 19

The Cross-Section for Spin-1/2 Targets Useful relation: Contracting hadronic and leptonic tensors we get: For a longitudinally polarized lepton beam, the polarization is where is the lepton helicity. 2004, Torino Aram Kotzinian 20

Longitudinally Polarized Target A target polarized along the incident beam direction: where for a target polarized parallel or antiparallel to the beam. in the evaluation of the cross-section Where the azimuthal angle f has been integrated over since the cross-section is independent on f. 2004, Torino Aram Kotzinian 21

Transversely Polarized Target The polarization vector of a transversely polarized target can be chosen to point along the in the Lab frame. So, the azimuthal angle of scattered lepton is counted from that direction. Then, in this case we get: The structure functions g 1 and g 2 are equally important for a transversely polarized target, and so an experiment with a transversely polarized target can be used to determine g 2, once g 1 has been measured using a longitudinally polarized target. 2004, Torino Aram Kotzinian 22

Details of derivation for unpolarized DIS Consider the general form of inelastic electron-proton scattering We must construct only from the available 4 -vectors, and the invariant tensors and. Thus we can write the most general structure in terms of the possible 6 tensors and corresponding form factors 2004, Torino Aram Kotzinian 23

Leptonic tensor is symmetric and we can ignore the antisymmetric terms in hadronic tensor for unpolarized DIS. Then conservation of the neutral current requires that , or, for arbitrary , Hence the coefficients of vanish and in this equation mustseparately Substituting back into the initial expression we have 2004, Torino Aram Kotzinian 24

In the laboratory frame we have the following relations between the kinematic quantities 2004, Torino Aram Kotzinian 25

Finally the definition of the cross section gives 2004, Torino Aram Kotzinian 26