Lecture survey v In the paper infront of

Lecture survey v In the paper in-front of you, please answer the MCQs v Timing : 7 min v Benefits: your right answers will reflect how well you can do on the final exam v Marks : none Medical Physics 1

LOGO Medical Physics Dr. Khalid Alsafi Dr. Mawya A. Khafaji Dr. Eng. Sarah K. Hagi

Outline of the lecture 1 2 3 4 Introduction Ionising and non Ionising Radiation Dosimetry and Activity Dose Calculation 5 Interaction with Matter Medical Physics 3

You Should Know Medical Physics 4

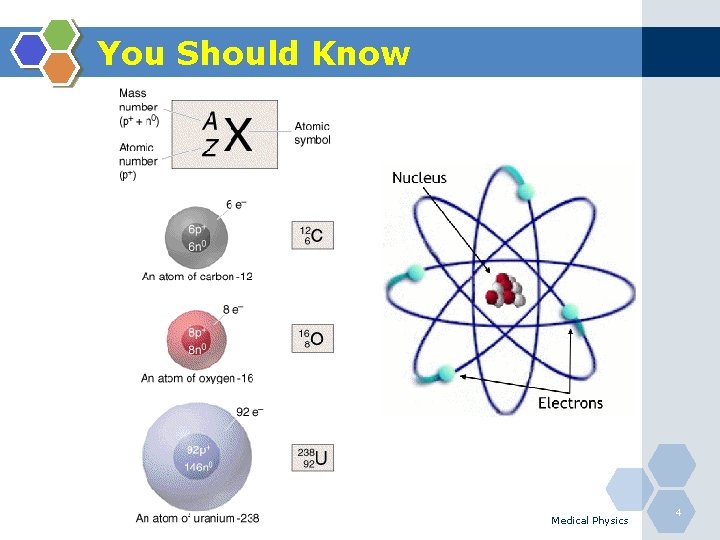
You Should Know Atom: The smallest particle of an element that can enter into a chemical reaction. Atomic number (Z): The total number of protons in the nucleus of an atom. Atomic mass number (A): The total number of protons and neutrons in the nucleus of an atom. Atomic weight: The mass of an atom, expressed in atomic mass units. For example, the atomic number of helium-4 is 2, the atomic mass is 4, and the atomic weight is 4. 00026. Medical Physics 5

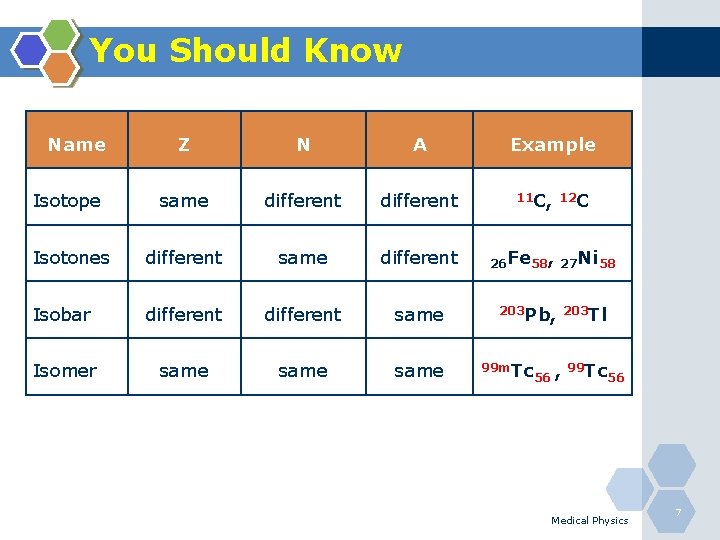
You Should Know v Atom consists of nucleus(+)& electrons(-) v Nucleus: protons(+) and neutrons(no charge) v Charge of protons = charge of electrons v Mass of protons 1840 X that of electrons v Isotopes: elements with the same Z and different N; (similar chemical properties) • • Z is the atomic number Z =Number of protons Z = Number of electrons A is mass number = Z+N Medical Physics 6

You Should Know Name Z N A Example Isotope same different 11 C, 12 C Isotones different same different 26 Fe 58, 27 Ni 58 Isobar different same 203 Pb, 203 Tl Isomer same 99 m. Tc 56 , 99 Tc 56 Medical Physics 7

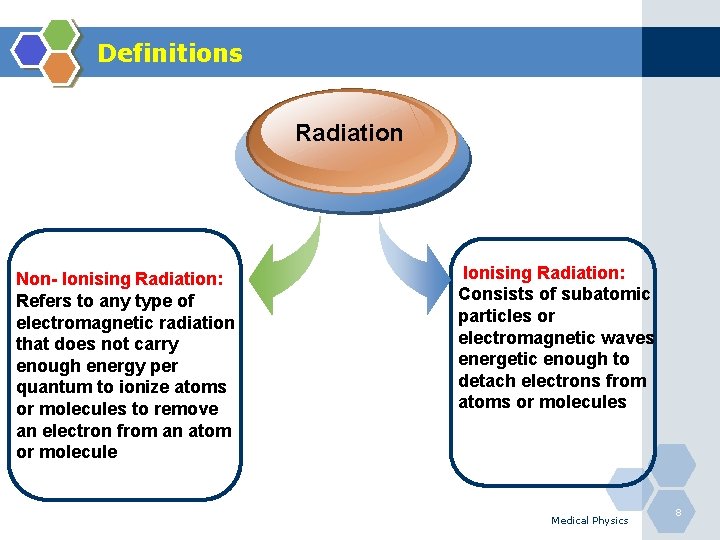
Definitions Radiation Non- Ionising Radiation: Refers to any type of electromagnetic radiation that does not carry enough energy per quantum to ionize atoms or molecules to remove an electron from an atom or molecule Ionising Radiation: Consists of subatomic particles or electromagnetic waves energetic enough to detach electrons from atoms or molecules Medical Physics 8

Ionizing radiation v Radiation with enough energy to remove tightly bound electron from their orbit when interacting with matter, other atoms; causing atoms to become charged or ionized v Given off by radioactive material, X-ray tubes, particles accelerators, nuclear reactions and is present in the environment v It is invisible and not directly detectable by human senses, needs special instruments to detect and measure it Medical Physics 9

Radiation in Radiology v Ionizing radiation is used daily in hospitals for diagnostic imaging procedures (disease and injury) v Most common forms of ionizing radiation are x rays and gamma rays v Benefits outweigh any potential small risk of harm from amount of radiation used Medical Physics 10

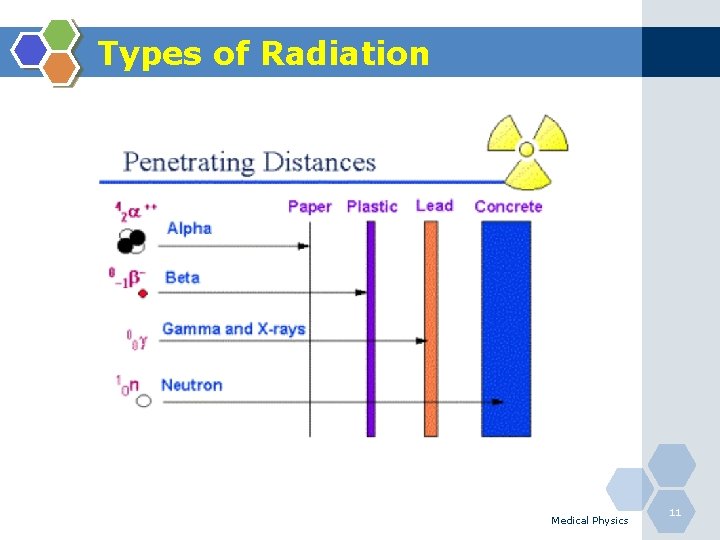
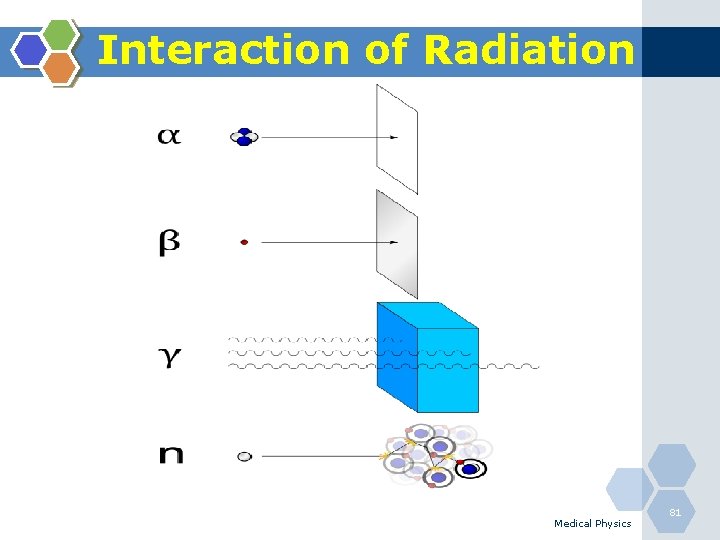
Types of Radiation Medical Physics 11

Direct Ionisation (Charged Particles) • Alpha-particles(α): The nucleus of a helium atom, made up of two neutrons and two protons with a charge of +2. Alpha particles generally carry more energy than γ and β. Alpha particles can be stopped by a sheet of paper and cannot penetrate the dead layer of skin. Therefore, they do not damage living tissue when outside the body. When alpha-emitting atoms are inhaled or swallowed, however, they are especially damaging because they transfer relatively large amounts of ionizing energy to living cells. Medical Physics 12

Direct & Indirect Ionisation (Charged Particles) • Beta-particles (β): Electrons ejected from the nucleus of a decaying atom. Although they can be stopped by a thin sheet of aluminium, beta particles can penetrate the dead skin layer, potentially causing burns. They can pose a serious direct or external radiation threat and can be lethal depending on the amount received. They also pose a serious internal radiation threat if beta-emitting atoms are ingested or inhaled. Medical Physics 13

Direct & Indirect Ionisation (Charged Particles) Electrons and Positrons (B+ and B-) Causes ionization; very light; travels in body Can be stopped by plastic sheet Medical Physics 14

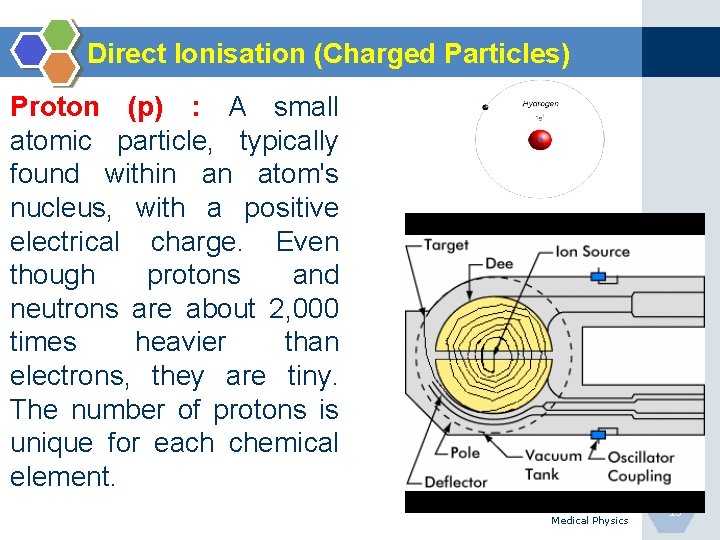
Direct Ionisation (Charged Particles) Proton (p) : A small atomic particle, typically found within an atom's nucleus, with a positive electrical charge. Even though protons and neutrons are about 2, 000 times heavier than electrons, they are tiny. The number of protons is unique for each chemical element. Medical Physics 15

Direct Ionisation (Charged Particles) Direct Ionisation Medical Physics 16

Direct Ionisation (Uncharged Particles) • Neutrons (n): A small atomic particle possessing no electrical charge typically found within an atom's nucleus. Neutrons have neither a positive nor a negative charge. A neutron has about the same mass as a proton. Medical Physics 17

Indirect Ionisation Photons (gamma (γ)): Discrete "packet" of pure electromagnetic energy. Photons have no mass, no charge and travel at the speed of light. Gamma rays originate in the nucleus. X-ray: Electromagnetic radiation caused by deflection of electrons from their original paths, or inner orbital electrons that change their orbital levels around the atomic nucleus. X-rays, like gamma rays can travel long distances through air and most other materials. X-rays and gamma rays differ primarily in their origin: x-rays originate in the electronic shell. Medical Physics 18

Photons ( Gamma and X-ray) v No charge v No mass v Indirect/secondary ionization v Gammas and x-rays differ only in their origin. v Both are electromagnetic radiation. v They travel with the speed of light Medical Physics 19

Gamma Vs. X-ray Gamma X-Ray Mass No No Speed Light Charge No No Origin Nucleus Orbital Medical Physics 20

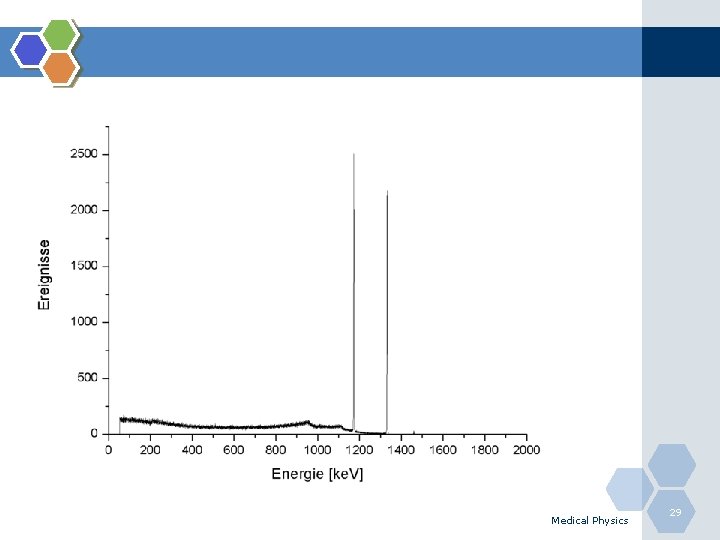
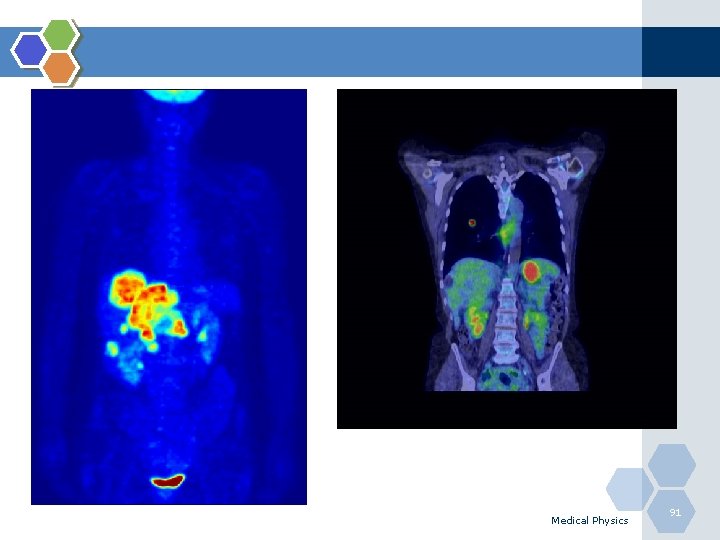
Common Use of Photons Common photon emitters A. Caesium ( 137 Cs ) B. Technetium (99 m. Tc) used in NM C. Iodine (131 I) used in NM Common Use: Diagnosing diseases or Cancer treatment Medical Physics 21

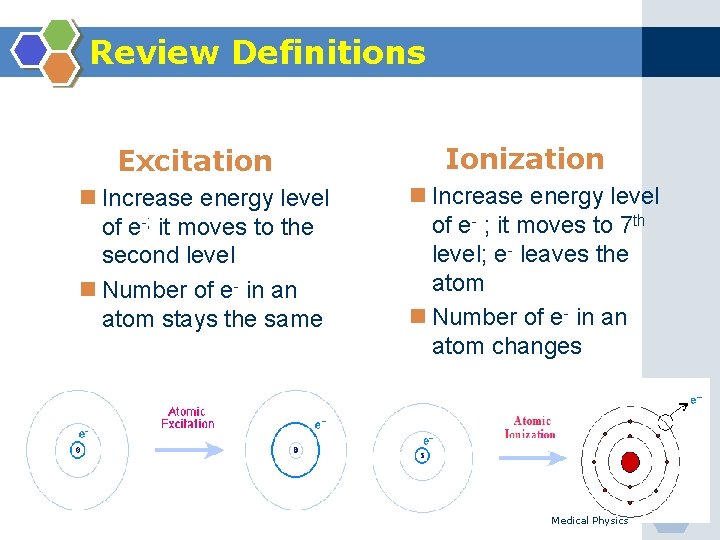
Review Definitions Excitation n Increase energy level of e-; it moves to the second level n Number of e- in an atom stays the same Ionization n Increase energy level of e- ; it moves to 7 th level; e- leaves the atom n Number of e- in an atom changes Medical Physics 22

Non-Ionizing Radiation v Radiation without enough energy to remove e- (not carry enough energy to ionize atoms or molecules) v Such as that emitted by a laser v It does not create ions when it interacts with matter § Dissipates energy generally in the form of heat v Has energy only for excitation Medical Physics 23

Examples of Non-Ionising Radiation v Ultra violet, Infrared, Microwave, Radio frequency, Static field v Non-ionizing radiation benefits: § Microwave - telecommunications and heating food § infrared radiation --infrared lamps to keep food warm in restaurants § radio waves-- broadcasting Medical Physics 24

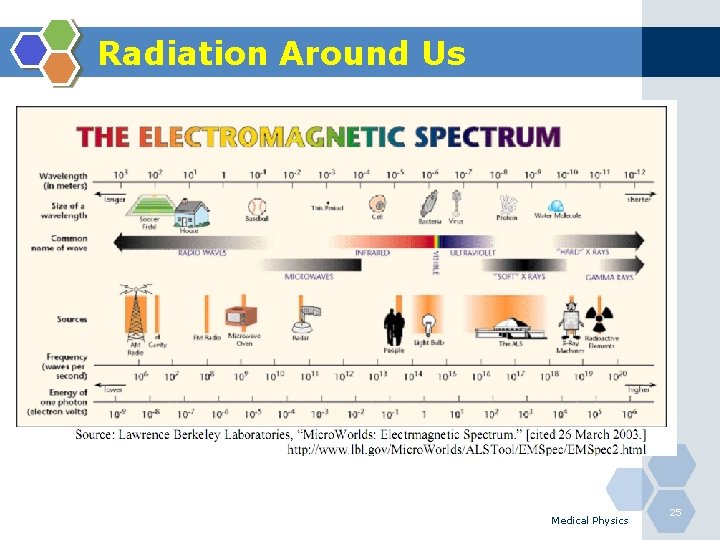
Radiation Around Us Medical Physics 25

Basic terms v Radiation: Energy traveling, either as particles or electromagnetic waves v Radioactive : Nuclides which undergo natural or induced transformation or decay of an atomic nucleus. v Dose: The amount of energy delivered to a subject per unit mass. Medical Physics 26

Source Activity and Units v Activity (A) can be defined in terms of the number of radioactive atoms N decaying per unit time (t). v (SI) unit for activity is the Becquerel (Bq) 1 Dis/Sec = 1 Becquerel v 1 Ci = 3. 7 x 104 MBq v Activity is not identical to the total number of radiations emitted per second, as can be seen from the following example: Medical Physics 27

Source Activity and Units Gamma v. Cobalt-60(60 Co) Beta emitter. v. Each disintegration has (β-) particle & 2 gamma giving a total radiation emission of 3/Bq. 1. 17 Me. V β- 60 Co Gamma 1. 33 Me. V 28 Medical Physics

Medical Physics 29

Activity Unit (Example) Q. 15 millicuries of 99 m. Tc is equal to how many MBq? Medical Physics 30

Activity Unit (Example) Answer. As 1. 0 m. Ci= 37 MBq 15 m. Ci x 37 MBq/m. Ci=555 MBq Medical Physics 31

Radioactivity and Decay In order to understand safety in radiation environments, it is essential to introduce the concept of radioactivity and its related terms. Activity (A) can be defined in terms of the number of radioactive atoms N decaying per unit time (t). The formal expression is: A=∆N/∆t Medical Physics 32

Radioactivity and Decay The activity of a radionuclide decreases exponentially with time. If N represents the number of atoms of a radionuclide in a sample at any given time, then the change d. N in that number during a short time dt is proportional to N and to dt. d. N= -λNdt where λ is the decay constant Medical Physics 33

Radioactive Decay Equations Where A is the activity at time t and A 0 is the original activity at time t 0 = 0 Medical Physics 34

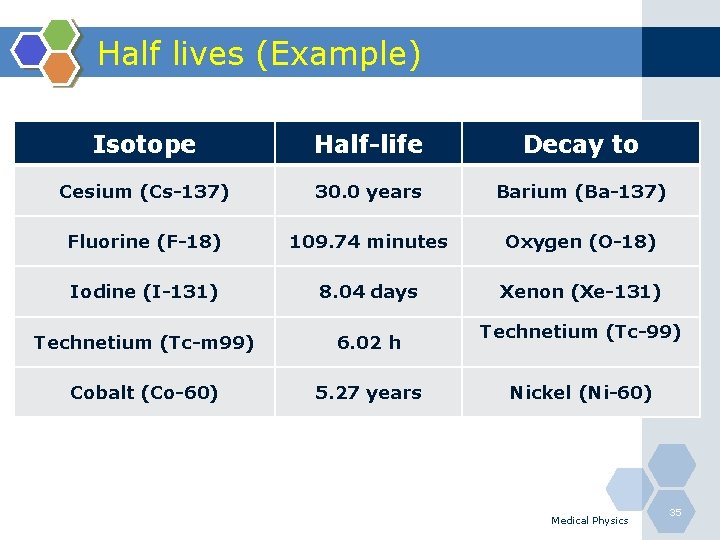
Half lives (Example) - Isotope Half-life Decay to Cesium (Cs-137) 30. 0 years Barium (Ba-137) Fluorine (F-18) 109. 74 minutes Oxygen (O-18) Iodine (I-131) 8. 04 days Xenon (Xe-131) Technetium (Tc-m 99) 6. 02 h Cobalt (Co-60) 5. 27 years Technetium (Tc-99) Nickel (Ni-60) Medical Physics 35

Half Life Time v. Half life is the time required by a radioisotope for its original activity to be reduced by one half, and which is unique for each isotope. Decay constant Medical Physics 36

Half lives (Example) Q. How does the half-life affect an isotope? Let's look closely at how the half-life affects an isotope. Suppose you have 10 grams of Barium-139. It has a half-life of 86 minutes. After 86 minutes, half of the atoms in the sample would have decayed into another element, Lanthanum-139. Therefore, after one half-life, you would have 5 grams of Barium-139, and 5 grams of Lanthanum-139. After another 86 minutes, half of the 5 grams of Barium-139 would decay into Lanthanum-139; you would now have 2. 5 grams of Barium-139 and 7. 5 grams of Lanthanum 139. Medical Physics 37

Example (1) Q. A radioactive isotope has a half-life of 3 years, initial activity is 100 MBq. What is the residual activity after 700 days? Medical Physics 38

Example (1) Medical Physics 39

Example (2) Q. What is the residual activity of 131 I after 3 days if the original activity was 1. 3 MBq and T 1/2 = 8. 04 days? Medical Physics 40

Example (2) Medical Physics 41

Example (3) Q. A vial containing 99 m. Tc is labeled “ 0. 50 MBq” at 3 pm; what is the activity at 9 am on the same day; the half-life of 99 m. Tc is 6 hours? Medical Physics 42

Example (3) Medical Physics 43

Number of Half lives From the definition of half-life, the fraction of a radioisotope remaining after n half-lives can be calculated by the following expression: Medical Physics 44

Example (4) Q. After how many half lives the residual activity will reached 1%? Medical Physics 45

Example (4) Medical Physics 46

Biological, Physical & Effective Half-lives What determines how long a radionuclide will irradiate the body? The combination of the physical(T 1/2) and biological(TB) half-life. The effective (Teff) half-life determines how long a radionuclide will continue to pump out energy into surrounding tissue. Medical Physics 47

Biological and Effective Half lives The biological half-life (TB) is the time the body takes to remove half of the radioactive nuclide. Effective half-life (Teff): The time required for the amount of a radionuclide deposited in a living organism to be diminished by 50% as a result of the combined action of radioactive decay and biologic elimination. Medical Physics 48

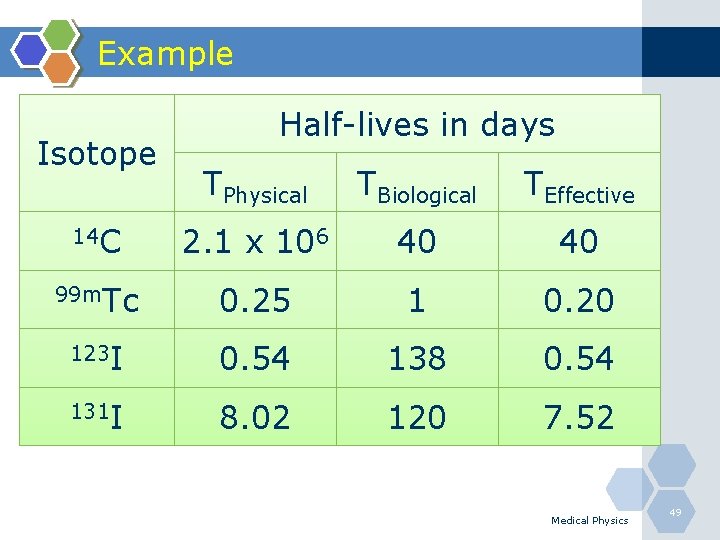
Example Isotope Half-lives in days TPhysical TBiological TEffective 14 C 2. 1 x 106 40 40 99 m. Tc 0. 25 1 0. 20 123 I 0. 54 138 0. 54 131 I 8. 02 120 7. 52 Medical Physics 49

Example (5) Q. If a patient is given a radioactive isotope which has a half-life of six days and a biological half-life of ten days, what is the effective half-life for the isotope? Medical Physics 50

Example (5) Medical Physics 51

Example (6) Q. Determine the effective half-life of 131 I (T 1/2=8. 02 days) in the human thyroid if it is removed with a biological half-life of 120 days? Medical Physics 52

Example (6) Medical Physics 53

Break for 15 min Medical Physics 54

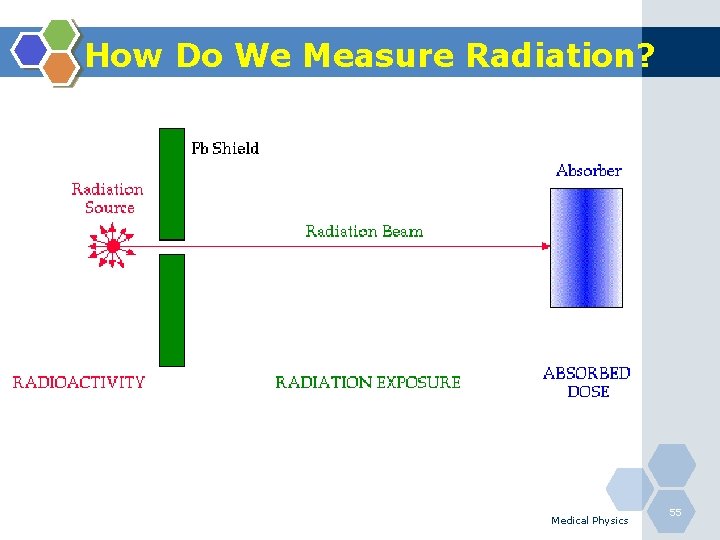
How Do We Measure Radiation? Medical Physics 55

Dose Calculations 1. Absorbed Dose (D) 2. Equivalent Dose (HT) 3. Effective Dose (Deff) Medical Physics 56

Units and Dose Calculations 1. Absorbed Dose (D): is a physical quantity which represents the energy imparted by radiation onto an absorbing material. Gray (Gy) - SI Unit 1 Gy = 1 joule per kilogram Medical Physics 57

Units and Dose Calculations 2. Equivalent Dose (HT): The concept of dose equivalent was introduced by the International Commission on Radiological Protection (ICRP). Dose equivalent (HT) can be defined as a quantity that takes into account the Relative Biological damage or Effectiveness (RBE = the ratio of the absorbed dose of a reference radiation, usually X-ray, to the absorbed dose of a test radiation required to produce the same level of effect ) caused by radiation interacting with tissue. Medical Physics 58

Units and Dose Calculations 2. Equivalent Dose (HT): Tissue damage per Gy of absorbed dose depends on the type and energy of radiation. The SI unit of equivalent dose is the Sievert (Sv). Equivalent does is correlated to absorbed dose D by, HT = ∑ D Q Sv Q is the quality weighting factor for different radiation types in the calculation of equivalent dose Medical Physics 59

Radiation Energy Transfer Determinations To understand the way ionizing radiation causes injury and how the effects may vary in biologic tissue 2 important concepts must be studied: 1. Linear Energy Transfer (LET) 2. Relative Biologic Effectiveness (RBE) Medical Physics 60

Radiation Energy Transfer Determinations Linear Energy Transfer (LET) • Linear energy transfer is the average energy deposited by an ionizing radiation travelling through a material per unit length. • LET depends on the kind of radiation and the density of the material. • LET is described in units of ke. V per micro meter (µm= 10 -6 m). • Low-LET radiation (x-ray and gamma ray) mainly causes indirect damage to biologic tissues, which usually can be reversed by repair enzymes. • The higher the LET, the higher the biological damage through energy deposition along the particle track. Medical Physics 61

Radiation Energy Transfer Determinations Relative Biological Effectiveness The Relative Biological Effectiveness, RBE, is a useful way to compare and contrast the results observed in these studies. The relative biological effectiveness for a given test radiation, is calculated as the dose of a reference radiation, usually x rays, required to produce the same biological effect as was seen with a test dose, DT, of another radiation. Thus, for the same biological endpoint, Dose from reference radiation REB=----------------Dose from test radiation, DT If it took 200 m. Gy of x rays but only 20 m. Gy of neutrons to produce the same biological effect, the RBE would be 200/20 = 10 using x rays as the reference radiation. For radiation protection purposes, the International Commission on Radiological Protection, ICRP, has described the effectiveness of radiations of differing qualities by a series of Radiation Weighting Factors (ICRP 1991) shown in the following table. 62 Medical Physics

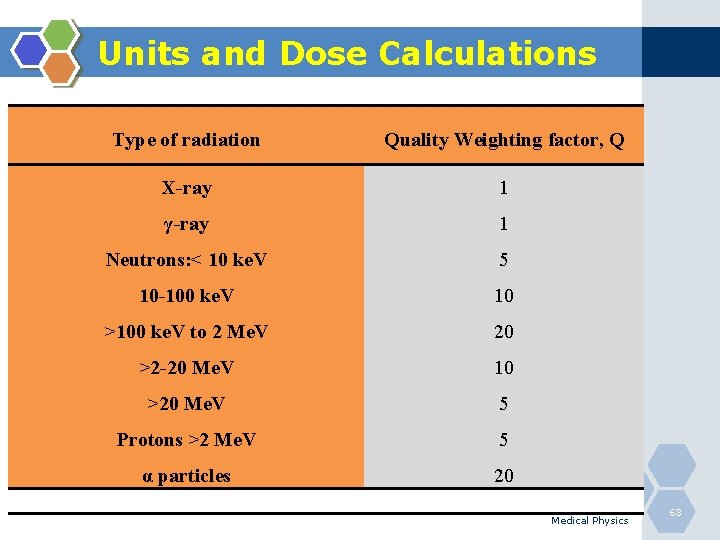
Units and Dose Calculations Type of radiation Quality Weighting factor, Q X-ray 1 γ-ray 1 Neutrons: < 10 ke. V 5 10 -100 ke. V 10 >100 ke. V to 2 Me. V 20 >2 -20 Me. V 10 >20 Me. V 5 Protons >2 Me. V 5 α particles 20 Medical Physics 63

Units and Dose Calculations Example: What is the equivalent dose to a worker who receives uniform, whole-body doses of 1. 0 m. Gy from 80 ke. V neutrons and 4 m. Gy from gamma rays ( Q for neutrons with energy 10 -100 ke. V is 10 and 1 for gamma and X rays)? Answer: HT = ∑ D Q HT = (1 x 10) + (1 x 4)=14 m. Sv Medical Physics 64

Units and Dose Calculations Example: During the year, a patient receives 5. 0 m. Gy from internally deposited alpha particles, 17 m. Gy proton particles and 10 m. Gy externally from uniform whole-body gamma irradiation, find the patient equivalent dose if( Q for alpha is 20, protons is 5 and 1 for gamma and X rays)? Answer: HT = ∑ D Q HT = (5 x 20) + (17 x 5)+ (10 x 1) =195 m. Sv Medical Physics 65

Units and Dose Calculations 3. Effective Dose (Deff): Deff = ∑ HT WR Sv The effective dose equivalent is used to compare radiation doses of different body parts. The effective dose (Deff) is found by calculating a weighted average of the equivalent dose (HT) with the weighting factors (w. R) designed to reflect the different radiosensitivities of the tissues, where Σ w. T = 1. The unit for effective dose is also the Sievert (Sv). Medical Physics 66

Units and Dose Calculations The sum is performed over all organs and tissues of the human body considered to be sensitive to the induction of stochastic effects. These w. R values are chosen to represent the contributions of individual organs and tissues to overall radiation detriment from stochastic effects. Medical Physics 67

Units and Dose Calculations The unit is the same for equivalent dose and effective dose. The organs and tissues for which w. R values are specified are given in next table. The follow-up studies of the survivors of the atomic bomb dropped on Japan in 1945 provide the main source of data on cancer risk for the older report. Medical Physics 68

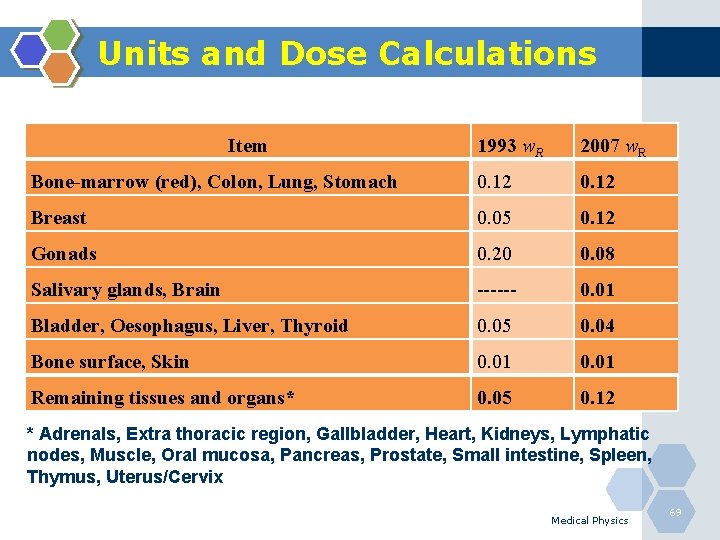
Units and Dose Calculations Item 1993 w. R 2007 w. R Bone-marrow (red), Colon, Lung, Stomach 0. 12 Breast 0. 05 0. 12 Gonads 0. 20 0. 08 Salivary glands, Brain ------ 0. 01 Bladder, Oesophagus, Liver, Thyroid 0. 05 0. 04 Bone surface, Skin 0. 01 Remaining tissues and organs* 0. 05 0. 12 * Adrenals, Extra thoracic region, Gallbladder, Heart, Kidneys, Lymphatic nodes, Muscle, Oral mucosa, Pancreas, Prostate, Small intestine, Spleen, Thymus, Uterus/Cervix Medical Physics 69

Units and Dose Calculations The breast weighting factor has increased by more than 200%. Meanwhile, the gonads w. R factor has decreased by 60%. Reasons for the significant change in both. The most recent report detailing recommendations of w. R is based on cancer incidence for both males and females in all age groups. Also, breast cancer is increasing in most of the developed and non developed countries. Medical Physics 70

Example Q. What is the effective dose to a worker who receives uniform, whole-body doses of 5. 0 m. Gy from 900 ke. V neutrons and 5 m. Gy from gamma rays ( Q for neutrons with energy 0. 9 Me. V is 20 and 1 for gamma and X rays) and (WR(Whole. Body)=1) Answer: HT = ∑ D Q HT = (5 x 20) + (5 x 1)=105 m. Sv Deff = ∑ HT WR Sv Deff = 105 x 1= 105 m. Sv Medical Physics 71

Example Q. A worker receives 7. 0 m. Gy from internally deposited alpha particles in the lung, 120 m. Gy beta particles in the thyroid and 10 m. Gy externally from uniform whole-body gamma irradiation, find the worker effective dose? (WR(Lung)=0. 12; WR(Thyroid)=0. 04; WR(Whole-Body)=1) and ( Q for alpha is 20 and 1 for gamma and X rays) Medical Physics 72

Example Answer: HT = ∑ D Q HT = (7 x 20) + (120 x 1) + (10 x 1) =270 m. Sv Deff =(7 x 20 x 0. 12)+(120 x 1 x 0. 04)+(10 x 1 x 1) Total-Deff = 31. 6 m. Sv Medical Physics 73

Example Alpha • 140 m. Sv • Lung (WR = 0. 12) • Deff=140 x 0. 12= 16. 8 m. Sv Beta • 120 m. Sv • Thyroid (WR = 0. 04) • Deff=120 x 0. 04= 4. 8 m. Sv Gamma • 10 m. Sv • Whole-body (WR = 1) • Deff=10 x 1= 10 m. Sv Total effective dose = 16. 8 + 4. 8 + 10= 31. 6 m. Sv Medical Physics 74

Example During the year, a physician receives 0. 6 m. Gy from internally deposited alpha particles in the lung, 40 m. Gy beta particles in the thyroid and 6 m. Gy externally from uniform wholebody gamma irradiation, find how much additional external, uniform, whole-body gamma dose could the worker receive during the year without technically exceeding the ? (WR(Lung)=0. 12; WR(Thyroid)=0. 05; WR(Whole. Body)=1)and ( Q for alpha is 20 and 1 for gamma and X rays) (ICRP=20 m. Sv/year) Medical Physics 75

Example Answer: HT = ∑ D Q HT = (0. 6 x 20) + (40 x 1) + (6 x 1) Deff =(0. 6 x 20 x 0. 12)+(40 x 1 x 0. 05)+(10 x 1 x 1) Total-Deff = 13. 44 m. Sv Staff can do more work= 20 -13. 44 =6. 56 m. Sv Medical Physics 76

Example Alpha • 12 m. Sv • Lung (WR = 0. 12) • Deff=12 x 0. 12= 1. 44 m. Sv Beta • 40 m. Sv • Thyroid (WR = 0. 04) • Deff=40 x 0. 05= 2 m. Sv Gamma • 10 m. Sv • Whole-body (WR = 1) • Deff=10 x 1= 10 m. Sv Total effective dose = 1. 44 + 2. 0 + 10= 13. 44 m. Sv Medical Physics 77

Break for 15 min Medical Physics 78

Interaction of Radiation Medical Physics 79

Interaction of Radiation Medical Physics 80

Interaction of Radiation Medical Physics 81

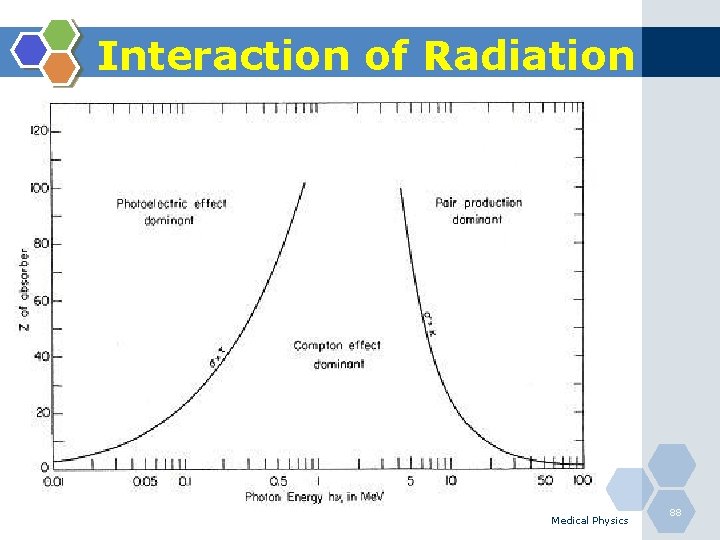
Interaction of Radiation 1. Photoelectric Effect 2. Compton Scattering Medical Physics 82

Photoelectric Effect (Complete absorption of incident photon) Medical Physics 83

Photoelectric Effect 1. The photoelectric effect is the most important interaction between lowenergy photons and high Z matter. 2. It is defined as an atomic absorption process in which an orbital electron completely absorbs the energy of an incident photon. 3. The photon disappears and the energy absorbed is used to eject the orbital electron from the atom. 4. The ejected electron is called a photoelectron and is most likely to be derived from the K-shell. 5. The electron receives kinetic energy Epe, equal to the difference between the incident photon energy Eo and the binding energy of the electron shell from which it was ejected. If a K-shell electron is ejected, the kinetic energy of the photoelectron is: Medical Physics 84

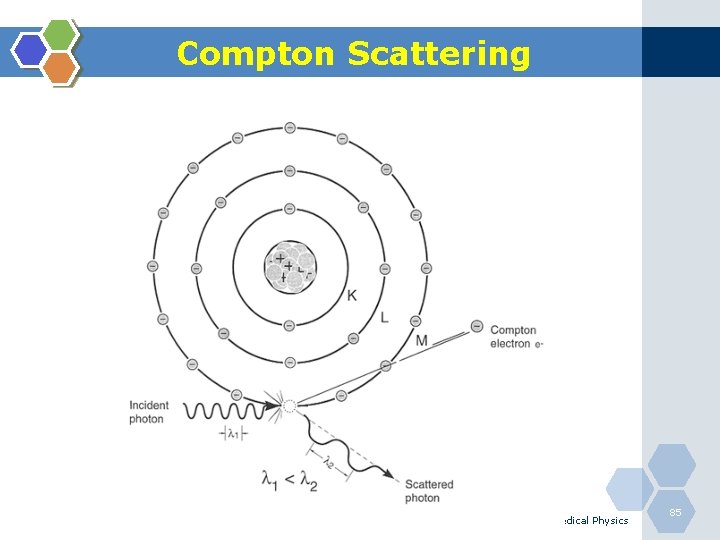
Compton Scattering Medical Physics 85

Compton Scattering 1. Compton scattering is a collision between an incident photon and a loosely bound outer shell orbital electron of an atom. 2. This interaction predominates for low-Z materials (e. g. tissue) and is in the region 0. 65 to 8 Me. V. 3. Since the incident photon energy greatly exceeds the binding energy of the electron to the atom, the interaction appears as a collision between the photon and a free electron. 4. However, the photon doses not disappear; instead it is deflected through a scattering angle (θ). 5. Part of its energy is transferred to the recoil electron; thus, the photon loses energy in the process. 6. The energy of the scattering photon is related to the scattering angle (θ) by consideration of energy and momentum conservation according to: Medical Physics 86

Compton Scattering Medical Physics 87

Interaction of Radiation Medical Physics 88

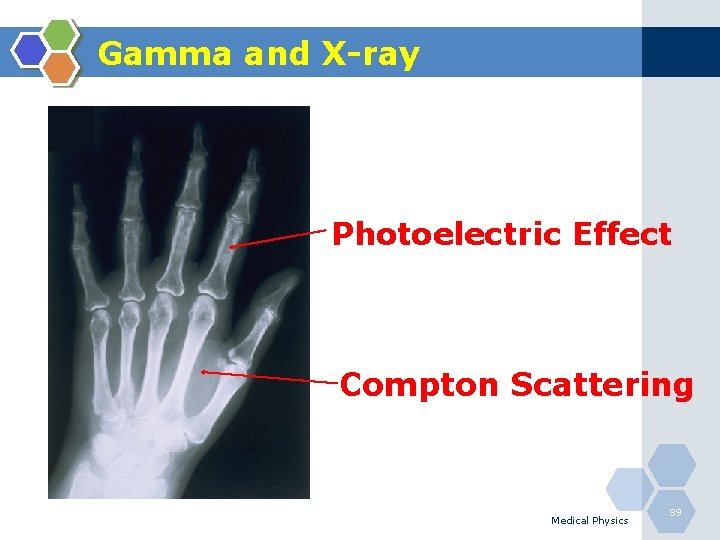
Gamma and X-ray Photoelectric Effect Compton Scattering Medical Physics 89

Compton Scattering With high energy photons Medical Physics 90

Medical Physics 91

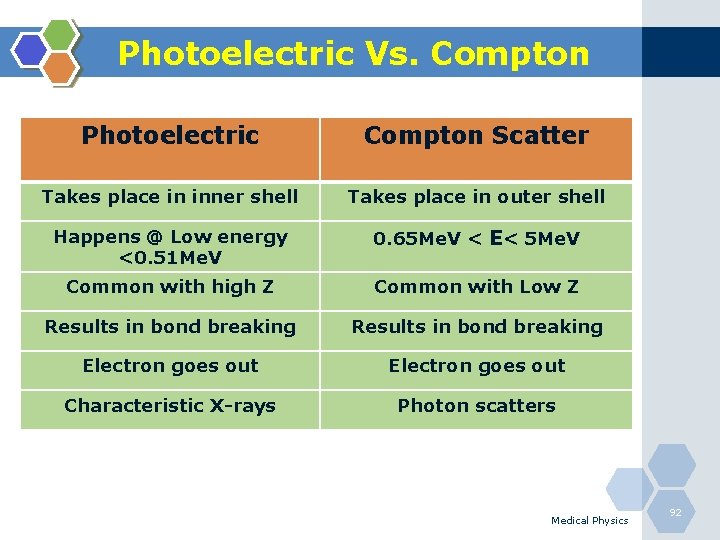
Photoelectric Vs. Compton Photoelectric Compton Scatter Takes place in inner shell Takes place in outer shell Happens @ Low energy <0. 51 Me. V 0. 65 Me. V < E< 5 Me. V Common with high Z Common with Low Z Results in bond breaking Electron goes out Characteristic X-rays Photon scatters Medical Physics 92

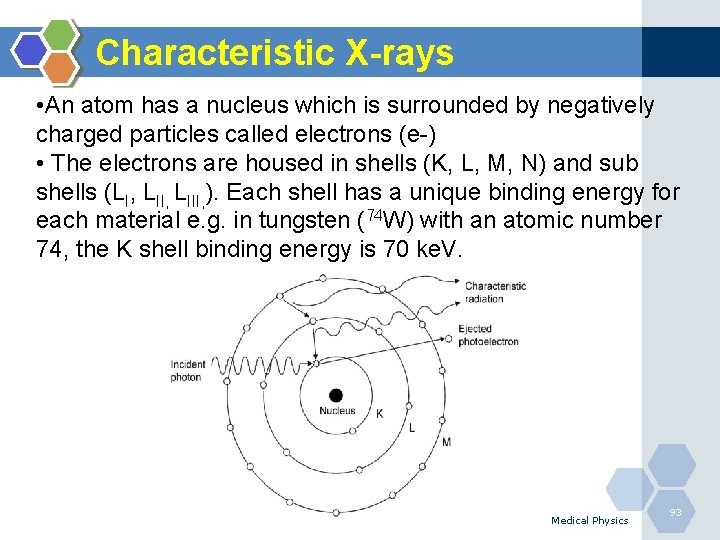
Characteristic X-rays • An atom has a nucleus which is surrounded by negatively charged particles called electrons (e-) • The electrons are housed in shells (K, L, M, N) and sub shells (LI, LIII, ). Each shell has a unique binding energy for each material e. g. in tungsten (74 W) with an atomic number 74, the K shell binding energy is 70 ke. V. Medical Physics 93

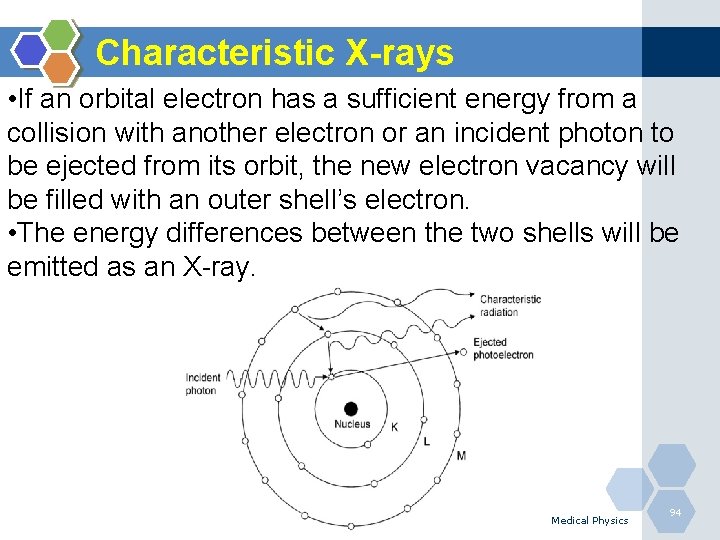
Characteristic X-rays • If an orbital electron has a sufficient energy from a collision with another electron or an incident photon to be ejected from its orbit, the new electron vacancy will be filled with an outer shell’s electron. • The energy differences between the two shells will be emitted as an X-ray. Medical Physics 94

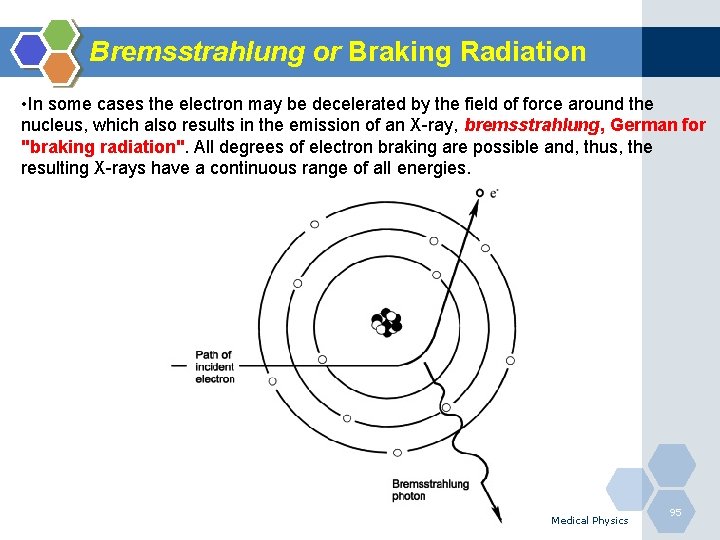
Bremsstrahlung or Braking Radiation • In some cases the electron may be decelerated by the field of force around the nucleus, which also results in the emission of an X-ray, bremsstrahlung, German for "braking radiation". All degrees of electron braking are possible and, thus, the resulting X-rays have a continuous range of all energies. Medical Physics 95

Linear attenuation coefficient (µ) This coefficient can be described as the total probability that a photon of a particular energy will undergo some kind of interaction with matter when travelling a unit distance through a particular substance. The value of µ (cm-1) generally increases as the Z of the absorber is increased, because photoelectric interactions are stronger in high Z materials, especially for low energy photons. It depends on the energy of the photon and atomic number (Z) of the absorber. Medical Physics 96

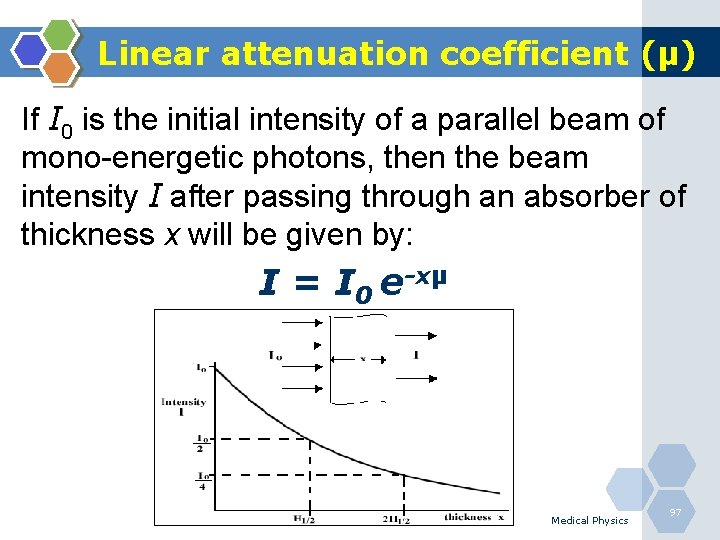
Linear attenuation coefficient (µ) If I 0 is the initial intensity of a parallel beam of mono-energetic photons, then the beam intensity I after passing through an absorber of thickness x will be given by: I = I 0 e-xµ Medical Physics 97

Example What is the required lead thickness to reduce the intensity by 1/2 if the linear attenuation coefficient is 23 cm-1? I/I 0= ½ and µ=23 cm-1 from I = I 0 e-xµ X=(ln 0. 5)/(-23) X=0. 03 cm=0. 3 mm Medical Physics 98

References • Attix, F. H. , Introduction to radiological physics and radiation dosimetry. 1 ed. 1986: Wiley-VCH. 628. • ICRP (1977) Recommendations of the International Commission on Radiological Protection, Ann ICRP 21, Nos. 1 -3. • ICRP (1991) Recommendations of the International Commission on Radiological Protection, Ann. ICRP 1, No. 3. • NCRP (1990) The Relative Biological Effectiveness of Radiations of Different Quality, NCRP Report No. 104, National Council on Radiation Protection and Measurements, Bethesda, MD. • Knoll, G. F. , Radiation Detection and Measurement. Third ed. 1999: Jon Wiley & Sons, Inc. • Greening, J. R. , Fundamentals of Radiation Dosimetry. Second ed. 1985: Taylor & Francis. 176. • Podgorsak, E. B. , Radiation Physics for Medical Physicists. 2006: Sprimger. 437. Medical Physics 99

Contact Details v Via Email: v sarahhagi@gmail. com v k. Alsafi@kau. edu. sa v Office (Basement next to MRI) v Lecture will be on site next week http: //mkhafaji. kau. edu. sa http: //kalsafi. kau. edu. sa Medical Physics 100

LOGO Medical Physics